Автоматический построитель конформных отображений

Автоматический построитель конформных отображений

Иллюстрации

Показать все

Реферат

 

Щ 1О4157

Класс 42d, 4

СССР

OllVICAHNE ИЗОЬР

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ

С. А. Гинзбург

АВТОМАТИЧ ЕСК И Й ПОСТРОИТЕЛ Ь КОН ФОРМ Н ЫХ

ОТО БРА)КЕН И Й

Заявлено 23 ноября 1953 и. за Л! 260<)0/45316!) в Миниетер "тво машиностроения и,яра)бороетроения СССР

Изобретение относится к области электромеханических счетно-решающих приборов и представляет собой автоматический построитель конформных отображений, предназначенный для решения уравнений вида:

4(х)+1!(х)+ . +f (х)+ +

+f, (х) =О, где слагаемые функции f „(x) и корни уравнения могут быть выражены комплексными величинами.

Решение основано на последова-! е;!ьном «опросе» всей комплексной !!лоскости независимого переменног > н нахождения значения его, удовлет-! воряющего заданному уравнению.

В предлагаемом устройстве, анало гично известным устройствам, ам1;литуда синусоидального напряжения соответствует модулю, а фаза — аргументу комплексной величины. Отличительной особенностью !!редлагаемого устройства является о, что в нем преобразование плоскости Z в плоскость 1Г производится путем введения переменно Z в модель функции г (Л) и записи полученного отображения на диаграмме с помощью следящих систем или на экране электронно-лучевой трубки.

Преобразование плоскости W в плоскость Z производится в устройстве путем непрерывной принудительной развертки переменной Z на комплексной плоскости и отметки тех значений Z на диаграмме, которые соответствуют заданным значениям IV.

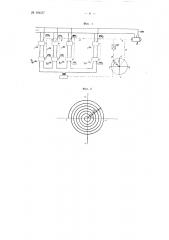
На фиг. 1 представлена скелетная схема устройства; на фиг. 2 — диаграмма спирали комплексной плоскости, независимого переменного;

»а фиг. 3 — диаграмма спирали комплексной плоскости независимого переменного, на которой обозначены области расположения корней уравнения при заниженной (грубой) чувствительности нуль-органа; на фиг. 4 — представлена схема устройства для решения уравнений вида:

ao+a,х+а х2+.... +а„х" =О.

Автоматический построитель конформных отображений предназначен для решения уравнений вида:

fo(õ) +f (-.) + ... +f (х) + .... +

+ f (х) = О, (1).

В этом уравнении слагаемые функции f; (х) и корни уравнения могуг ()b!Tk выражены комплексными величи)! !! м!!.

Комплексные величины можно представить !) показательной форме:

f,, (х) - — В, 1!". (2)

«:=А . l) (3),) о )94 )57

Тогда уравнение (1) приобретет следующий вид:

В,Р—,— В,. Р + ... + В,. 1 " +... +

+ В,. И „-- О. (1О)

Модули В; и аргумент j3; есть .функции модуля А и аргумента .".

При обходе комплексной плоскости независимого переменного по спирали (фиг. 2), т. е. при вводе пройорцйональной связи между его модулем и аргументом, А=к, (5) если требуется m оборотов вектора независимого переменного, необходимых для того, чтобы его модуль -jo— стиг значения А,, определяется коэффициент пропорциона. IF:öoñòa К гпту х

К -- "" (6) m

Таким образом, м дули В; и аргументы 3; становятся уже функциями только одного переменного (или а, или А) например:

В,. -= ъ,. (Ы, (7)

- г (х). (8)

Скелстная схема устройства, представленная на фиг. 1, состоит из фазовых модуляторов Ф.И0, Ф И,...

; .. ФИ„, подключенных к сети переменного -îêà, .вы.ходы которы.х подключены к входам амплитудных модуляторов А И0, АЛ) ... ЛМ, . Выходные напряжения амплитудных модуляторов суммируются между собой и подаются на нуль-орган НО.

Аргумент независимого переменного выражаешься углом поворота оси, непрерывно врашаемой от приводпого двигателя Д. Эта ось вращает рычаг P над диаграммой и через редуктор РД с передаточным отношением =к перемещает по рычагу каретку

Т, которая обходит плоскость диаграммы по спирали (фиг. 2).

Ось управляет также всеми фазовыми и амплитудными модуляторами, которые должны быть построены так, чтобы отображать функции (7) и (8).

На выходе фазовых модуляторов получается напряжение постоянное по амплитуде, но изменяющееся по фазе соответственно функции (8) .

Амплитудные модуляторы, сохраняя фазу напряжения, изменяют амплитуду его соответственно функции (7) . Следовательно, на выходе ами,ппудных модуляторов получаются напряжения, соответствующие слагаемым уравнениям (4), Эти напряжения суммируются между собой и подаются в нуль-орган НО.

При непрерывном вращении оси и момент, когда сумма напряжений на выходе равна нулю (т. е. удов,-етворяется заданное уравнение: значение независимой переменной равно корню уравнения), нуль-орган

НО срабатывает и, воздействуя пиа элемент записи на каретке Т, ставит чочку на диаграмме, отмечая значспне корня. уравнения..

Применяя спиральную развертку, .ложно получить расположение корней уравнения на экране осциллографа.

При обходе по спирали к мплексной плоскости независимого перемен ного может получиться, что значение корня окажется между витками спирали и корень не будет отмечен. Чтобы этого не получилось, необходимо

coãласовать между собой число витков спирали и чувствительность нульоргана FIO.

При первом соходе комплексной плоскости нужно понизить его чувствительность. Тогда на диаграмме будут обозначены области расположения корней, как это показано на фиг. 3.

Hpè дальнейших обходах, при увеличении числа витков спирали и чувствительности НО, эти области будут сужаться, стремясь к точке, отображающей точное значение корня.

Когда каретка Т обойдет всю плоскость: диаграммы и дойдет до границы, двигатель Д автоматически реверсирует и начинается обход комплекснои плоскости в обратном направлении.

На фиг. 4 представлена схема устройства для решения, например, уравнений и-й степени с постоянными коэффициентами: а, + а,х + а.,х + ... — а,.х +... +

-+ а,х" = — О. (9)

Подставляя независимую переменную в виде комплексной величины в показательной форме (3), получим

¹ 104.157 уравнение (1). которое « данном случае приобретает следующий вид: а„; — а, Al " -, аЛ- /) -" -+-... —, 3Ä A"!1 " О. (1о)

Функции (7) и (8) «этом случае оказываются ра«нымп:

Ва адЛ- и() 1; ".(и (11)

3(/ »q:(. (12)

Таким образом, для д того слагаемого амплитуда должны быть возведены в степень q, а фаза умножена на величину (1.

В схеме д»г(1 рсlH HHH уравнения (9) «качеi Tвс фазовых модуляторов применены фазс(ращатели, представляющие собой двухфазный статор, создающий вращающееся поле, и однофазньш ротор, фаза напряжения в котором пропорциональна углу поворота, Ротор нулевого фазовращателя неподвижен. Он определяет положение координатных осей на диаграмме. Ротор первого фазо«ращателя связан с осью ()» которая приводится во вращение двигателем Д через передачу 1; 1. Роторы последующих фазоврашатслей приводятся во вращение от той же оси ((через такие передачи, что за один оборот Оси (( эти роторы совершают 2, 3... (г оборото«, т. с. аргумент соответственно возрастает в 2, 3... и раз, как это требуется равенством (12).

Через передачу с передаточным

mi» числ011 К вЂ” от оси п привоЬ л дится во «ращение ось, уира«ляюгцая амплитудными модуляторами, представляющими субои реостат:(ые датчики. Первый амплитудньш модулятор содержит одно рсоста(нос звено, второй — — два последовательно включенных звена и т. д. до 11 звеньев. В результате амплитуда в первом звене линейно зависит от ((, во втором — пропорциональна ((- и т. д. до уды«летьоряя равенству (11).

Реос1 111 Hь(е „(аз ((11

Для установки значений постоянных коэффициентов и), аь a,... а„ сллкат реостаты HH ьыходс амплитудных ((О;((.ляторов, Предмет изобретения

» »13 1 03(1(тll»(ЕСКИИ 1(OCTPOHT(; HOHфорх(ных отображений, представляю(цих собой электромеханическое устройство, в котором амплитуда синусоидальног0 напряжения соответствует модулю, а фаза — аргументу кОмп,((»1»с«011 «(,!нчинь(. О т;1 и ч а ющ it и с я тем, что преобразование

flP(ocIi0cTH 7 13 плс I(OOTb OE IlpÎH«I30дится путем»E)nc(IHH переменной Z в модуль фун i((HEI F (Z) и записи Нолучешнэг() отображения Н3 диаграмме с помо)н(»10 следящих 01(стем или на экране э, (ектронно-луче«ой трубпреооразоваEIHP Il (()ClxOCTH 1Г « плос(»ость 7 произ«()дится путем непрерывной принудит(I(".I )I3 развертки переменной Л на комплекс 101( плоскосги и отметки тех значений Л на диаграмме, которые соот«стствуют заданным значениям 1Г.