Наглядное пособие для демонстрации действий над векторами

Наглядное пособие для демонстрации действий над векторами

Иллюстрации

Показать все

Реферат

 

НАГЛЯДНОЕ ПОСОБИЕ ДЛЯ ДЕ- , монстрАций дайствий НАД ВЕКТОРАМИ, состоящее из набора стержней и подвижной опоры, отличающеес я тем, что, с целью расширения диапазона решаемых задач, оно содержит набор разноцветных пластин, ,выполненных в виде параллелограмма, длины сторон которого равны длинам соответствующих стержней набора, и шар с радиально расположенными отверстиямидля закрепления в них кон-. цов стержней, жестко закрепленный на подвижной опоре, при этом каждый стержень имеет продольные направляющие для установки пластин и цветовую индикацию.

СОЮЗ СОВЕТСНИХ

ОИ а

РЕСПУБЛИК

09) (11) 3(59 0 09 В 23 00

ОПИСАНИЕ ИЗОБРЕТЕНИЯ ..

ГОСУДАРСТВЕННЫЙ НОМИТЕТ СССР

ГЮ ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ

:«(21) 3482941/18-21 (22) 09.08.82 (46) 07.11.83. Бюл. М 41 (72) Ю.Н. Попов, И.Н. Матысек и Л.Н. Морозова (71). Горловский Филиал Донецкого ордена Трудового Красного Знамени политехнического института (53) 513(088. 8) (56.) 1. Авторское свидетельство СССР

В 411488, кл. G 09 В 23/00, 1974. (54)(57) НАГЛЯДНОЕ ПОСОБИЕ ДЛЯ ДЕМОНСТРАЦИИ ДЕЙСТВИЙ НАД ВЕКТОРАМИ состоящее из набора стержней и подвижной опоры, о т л и ч а ю щ е ес я тем, что, с целью расширения диапазона решаемых задач, оно содержит набор разноцветных пластин, : выполненных в виде параллелограмма, длины сторон которого равны длинам соответствующих стержней набора, и шар с радиально расположенными отверстиями для закрепления в них концов стержней, жестко закрепленный на подвижной опоре, при этом каждый стержень имеет продольные направляющие для установки пластин н цветовую индикацию.

1053134

Изббретение относится к учебным приборам и наглядйым пособиям по механике и математике и может быть .использовано в учебном процессе высших и средних специальных учебных заведений..

Известно наглядное пособие, содержащее набор стержней, и подвижную опору. При помощи этого пособия можно демонстрировать сложение, вычитание и разложение векторов по двум направлениям Pj .

Недостатком известного наглядного пособия для демонстрации действий над векторами является то, что оно не может быть использовано для демонстрации векторного произведения и его свойств.

Целью,изобретения является расширение диапазона решаемых задач.

Поставленная цель достигается тем, что наглядное пособие для,демонстрации действий над векторами, состоящее из набора стержней и под-, вижной опоры, содержит набор разно- . цветных пластин, выполненных в виде параллелограмма, длины сторон которого равны длинам соответствующих стержней набора, и шар с радиально расположенными отверстиями для эакрегления в них концов стержней, жестко закрепленный на подвижной опоре, при этом каждый стержень имеет продольные направляющие для установки пластин и цветовую индикацию.

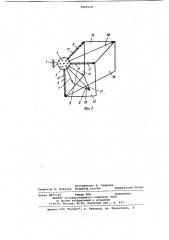
На фиг. 1 изображено наглядное пособие при демонстрации суммы, разности и произведения векторов, на фиг. 2 — то же, при демонстрации произведения векторов и его свойств.

Наглядное пособие содержит подвижную опору 1, шар 2 с радиально расположенными отверстиями 3, на, бор стержней 4 — 10, каждый из которых имеет направляющие пазы 11 и

12 и набор пластин в виде паралле лограммов 13 — 17 с диагоналями

18-20 ° Диагональ 19 представлена стержнем 9. Стержня являются смежными сторонами параллелограммов.Так, .смежными сторонами параллелограмма

15 - стержня 5 и 6, параллелограмма 16стержень 4 и диагональ 18 параллелограмма 15, на которой выполнен паз

11, пластины 17 - стержни 7 и 8, на параллелограмме 17 нанесена диагональ, которая по длйне равна длине стержня 9. Длина стержня 8 равна длине

>стержня 10. Центр шара является исходной точкой приложения векторов.

Каждый из элеМентов наглядного пособия иллюстрирует определенные математические. понятия, а именно стержень 4 иллюстрирует понятие

"вектор s" стержень 5 — "вектор Ь", стержень 6 - "вектор с", стержень

7 " "вектор в м b", стержень 8

"вектор s s c", стержень 9 — "вектор (ам Ь)Ф(àp )", диагональ 18

"вектор b + с", длины стержней соответствуют понятиям "модули векторов", пластины иллюстрируют понятия "плоскость параллелограмма", а их плошадь —,"модуль векторного произведе5 !

О ния", острые углы этих пластин соответствуют понятию "кратчайший поворот от одного вектора к другому".

Стержни 5 и 6 иллюстрируют разложение вектора (фиг. 1), изображенного диагональю 18 параллелограмма

15, по двум направлениям. Сумме векторов (b + с) соответствует диагональ 18 параллелограмма 15, а раэ20 ности векторов (b — с) — диагональ

20 параллелограмма 15.

Векторное произ ведение (Ь Х с ) и

его свойство .(b x с) = — (с х Ь) иллюстрируются следующим образом. Стержни 8 и 10 располагают соосно и перпендикулярно плоскости параллелограмма 15, построенного на векторах Ь и с. Стержень 8 соответствует понятию

"векторное произведение (bx с,", 30 стержень 10 — "векторное произведение (с x b)". Если смотреть на конец стержня 8 сверху, то кратчайший поворот от стержня 5 к стержню 6, т.е.

b к с, производится против часовой

35 стрелки, значит стержень 8 действительно соответствует b x с. Аналогичго можно убедиться, что стержень . 10 соответствует с х b. Поскольку направления стержней 8 и 10 противопо40 ложны, формула (Ь х с) = -(c хЬ) очевидна, Рассматривают сочетательный закон (a b ) + (s g с ) = -. х (Ь + с ). Векторному произведению (a 4 b ) соответствуетт стержень 7, а (а х с) — стержень

45 8, сумме векторов («ах Ь ) + (a ax c ) диагональ 19 пластины 17. Сумме векторов (Ь + c) соответствует диагональ 18 пластины 15, а векторному произведению В.x (b + с) — стержень

50 9, который перпендикулярен пластине

16 и равен диагонали 19 пластины

17, следовательно формула (a х с) +

+ (a,х Ь) = aaх (Ь + с) очевидна.

С целью повышения дидактического

55. эффекта элементы наглядного пособия выполнены различными по окраске.

Использование наглядного пособия поэ" воляет повысить дидактический эффект обучения.

10531 34

g nr 1Z (Pub. Г

Составитель Б. Андреев

Редактор Н. Бобкова Техред М. Костик КорректорА.Тяско

Закаэ 8877/48 ТИраж 488 Подписное

ВНИИПИ Государственного комитета СССР по делам иэобретений и открытий

113035, Москва, Ж-35, Раушская наб., д. 4/5

Филиал ППП "Патент", г. Ужгород, ул. Проектная, 4