Устройство для вычисления полиномов

Устройство для вычисления полиномов

Иллюстрации

Показать все

Реферат

 

УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ iПОЛИНОМОВ, содержащее m сумматоров, , (т+1) регистров коэффициентов и регистр аргумента, выходы которого подключены к первым входам сумматоров , вторые входы которых связаны с выходами соответствукидах регистров коэффициентов, о т л и - чающееся тем, что, с целью повьшения быстродействия, в устройство введены (m+l) блоков постоянной памяти и суммирующий блок, входы которого соединены с выходами (m+I)-го регистра коэффициентов и с выходами блоков постоянной памяти , входы m из которых соединены с выходами соответствукндих сумматоров , входы (тч-1)-го блока пЪстоян (Л ной памяти подключены к выходам регистра аргумента, а выходы сумми- . рующего блока являются выходами устройства . СП О о

СОЮЗ СОВЕТСКИХ

СОЦИАЛИСТИЧЕСКИХ

РЕСПУБЛИК

3(59 06 F 15 31

ОЛИСАНИЕ ИЗОБРЕТЕНИЯ

Н ABTOPCHOMV СВИДЕТЕЛЬСТВУ у,цр;. )т :

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР

ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ (21.) 3462690/18-24 (22 ) 05. 07. 82 (46 ) 15. 01. 84. Бюл. У 2 (72 ) В. И. Жабин, В.И, Корнейчук, В.В. Макаров и В.IT. Тарасенко (71) Киевский ордена Ленина политехнический институт им. 50-летия Великой Октябрьской социалистической революции (53 ) 681. 325 (088. 8 ) (56) 1. Патент Японии 9 49-28212, кл, G 06 F 15/00, опублик. 1974.

2. Благовещенский I0.A., Теслер Г.С. Вычисление элементарных функций на ЭБМ. Киев "Техника", 1977, с. 68-72.

3. Авторское свидетельство СССР

9 451088, кл. G F 15/31, 1972.

4. Авторское свидетельство СССР

Р 556446, кл. G 06 F 15/31, 1975.

5. Кнут Д. Искусство программирования для ЭВМ. Т. 2, М., "Мир", 1977, с. 511.

6. Щауман A.М. О новы машинной арифметики. Л., изд-во Ленинградского университета, 1979, с. 187.

7. Полупроводниковые запоминающие устройства. Под ред. А.Ю. Гордо; нова. И., "Радио и связь", 1981, с. 181.

8. Авторское свидетельство СССР

Р 868767, кл. G F 15/31, 1978 (прототип).

9 Справочник по интегральньм микросхемам. Под ред. М. Тарабрина. М- "Энергия", 1980. с, 124-1 86.

10. Карцев М.А, Брик В.A. Вычислительные системы и синхронная арифметика. M. "Радио и связь", 1981, с. 205.

„„Я0„„10675 A (54) (57) УСТРОЙСТВО gHSI ПОЛИИОМОВю содержащее ш сумматоров,, (ш+1) регистров коэффициентов и регистр аргумента, выходы которого подключены к первым входам сумматоров, вторые входы которых связаны с выходами соответствующих регистров коэффициентов, о т л и - . ч а ю щ е е с я тем, что, с целью повыаения быстродействия, в устройство введены (ш+1) блоков постоянной памяти и суммирующий блок, входы которого соединены с выходами (ш+1 )-гь регистра коэффициентов и с выходами блоков постоянной па мяти, входы m из которых соединены с выходами соответствующих сумматоров, входЫ (ш+1)-го блока постоянной памяти подключены к выходам регистра аргумента, а выходы суммирующего блока являются выходами устройства.

1067509

Изобретение относится к вычислительной технике и может быть применено в цифровых вычислительных машинах и устройствах.

Известны устройства, предназна-. ченные д я в исле ия полинчов 5 у(х)=а +ах + а х +...а х, пред

% tn ставляющие собой универсальные выч н слит ель ные машины 11 . Такие устройства содержат регистры, сумматоры, блоки управления, оперативное запоминающее устройство. Вычисление полиномов в них осуществляется путем выполнения соответствующих программ, например программ вычисления многочлена по схеме "Горнера.Для 35 выполнения этих программ необходимо осуществить m сложений и m умножений, где ш — степень полинома. Кроме того, затрачивается время на ббращение к памяти за операидами и 2О командами и на модификацию команд.

В случаях, когда вычислЕние полиномов необходимо производить многократно для различных значений аргумента X при фиксированных зна- -25 чениях коэффициентов а,:, используют-: ся методы предварительйой обработки коэффициентов, что уменьшает требуемое число умножений (23. В частности, для вычисления полинома шестой ЗО степени в этом случае необходимо выполнить, четыре умножения к семь сложений, т.е. на два умножения меньше, чем по схеме Горнера..

Недостатком устройства, в котором реализованы программные методы вычислений, является низкое быстро действие, что объясняется необходимостью не только многократного выполнения операций умножения и сложения, но и многократного обращения 4О к запоминающему устройству за командами и операндами, модификации команд и т.д.

Известны также устройства для вычисления полиномов, в которых ,реализованы аппаратурные методы вычислений, что поэ воляет,производить вычисление быстрее,чем в устройствах, работакиаих по программному прикцкпуК устройствам такого типа можно отнести устройс so для вычисления полинсиов вида х у С31, содержащее регистры оп рандов и промежуточных результатов, сумматоры, схемы И, блок управления; устрой- 55

cTso для вычисления полиноиов С41 содержащее регистр, сумматоры, ре« версивный счетчик, схему сразненкя, элементы И„ элемент задержки.

- Недостатком таких устройств так- 6О же является низкое быстродействие, Например, для вычисления полинома в первом из них необходимо выполнить m.n циклов вычислений, где

n - разрядность операндов каждый из которых состоит из суммирования и сдвига. Второе кз известных устройств производит вычисление полинома в следящем режиме и обладает низким быстродействием для больших рассогласований аргумента .

Известны также табличные устройства для вычисления полиномов, содержащие постоянные запоминающие

1 устройства для получения степеней х аргумента X и для умножения их на соответствующий коэффициент а- E51 ° Однако для табличной реализации умножения необходим большой объем постоянной памяти, равный

2 и бит, в связи с чем при разЪ рядности операндов n > 6 применение табличных мнонительных устройств затруднено Е61.

Поэтому применяют методы умноже« ния с использованием таблиц логарифмов и антилогарифмов, а также (что более экономично) таблиц квадратов чисел. Во втором случае умножение чисел Х и -Х осуществляется по формуле С7 1 х-x () -(=) X+Y Х-Y a

2 2

Однако и в этом случае необходим большой объем постоянной памяти.

Так, для реализации одного умножения необходимо иметь два блока постоянной памяти емкостью 2" и где и - разность операндов. для построения .табличного устройства, предназначенного.для вычксленкя полинома, накример. пятой степени, требуется четырнадцать блоков постоянной памяти. Четыре as них используются для вычисления значений ХЕ,XЗ,ХФ,XS к десять - для умножения следуюцнх пар чисел: а х а х, аз х, а„х", ад x® . СуввИрный объем постояниой памяти должен составлять 4(3" и)+10(2". п) бкт, что, например, прк п 12 будет иметь величину 688 К бит. Таким образом, известные табличные устройства требуют для кх построения большого объема оборудования.

Наиболее близким к предлагаемому является устройство для вычисленкя иногочленов вида Д. А; х, содержащее накапливакщие сумматоры, сдвиговые регистры, регистры операндов, регистры коэффициентов, Формирователи цифр, регистры цифры С83.

Перед йачалом вычислений в регистрах коэффициентов и суиматорах записаны коэФФициенты а, в регистрах операндов записан код аргумен- та Х. Вычисления в известном устройстве производятся в (2 hog<(m+1 )+и) циклах, каждый кз которых состоит

as суммирования и сдвига.

1067509

Недостатком известного устройства является низкое быстродействие.

Действительно, время вычислений составляет Т = (2 fog<(y+2)+n)»

«(С + t ), где 1 — время суммирования, tùä- время сдвига.

Целью изобретения является повышение быстродействия.

Поставленная цель достигается тем, что в устройство, содержащее и суввнвторов, (и+1(регистров ковф- (0 фициентов и регистр аргумента, выходи которого подключены к первьм. .входам суввюаторов, вторые входы которых связаны с выходами соответ ствующих регистров коэффициентов, 15 введены (в+1) блоков постоянной памяти и суммирующий блок, входы которого соединены с выходами (m+1)-ro регистра коэффициентов н с выходами блоков постоянной памяти, входы m 20 из которых соединены с выходами соответствующих сумматоров, входы (m+1)-ro блока постоянной памяти подключены к выходам регистра аргумента, а выходы суммирующего блока являются выходами устройства.

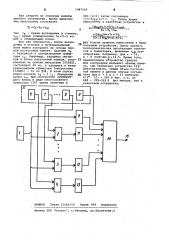
На чертеже изображена структурная схема устройства для вычисления полинсиов степени m.

Выходы регистра аргумента 1 подклю-О чены к йервым входам сумматоров 2-4, число которых равно ш (m - степень полинома), и ico входам блока постоянной памяти 5. Вторые входы каждого сувааатора 2-4 связаны с выходами регистров коэффициентов 6-8, число которых равно m. Регистры 6-9 входят в состав блока коэффициентов 10. Выходы каждого сумматора 2-4 соединены со входами блоков постоянной памяти

11-13, чиоло которых равно m. Вы- 40 ходы блоков 5, 11-13 и регистра коэффициентов 9 связаны со входами суммирующего блока 14, выходи которого подключены к выходам 15 устройства. 45

В блоки постоянной памяти 11-13 записаны таблицы возведения чисел в степень, причем блок постоянной памяти 11 предназначен для возведения числа в степень "2", блок пос- 5g тоянной .наняты 12 — для возведения в степень "3" и т.д., до блока постоянной памяти 13, который предназначен для возведения числа в степень m. В блок постоянной памяти 5 записана таблица функции -(x +õ +... ... +х ф+ хф").

° Суммирующий блок 14 предназначен для суммирования (m+2) .чисел и может быть построен, например, в виде дерева сумматоров.

Устройство предназначено для вычисления полинома с предварительной обработкой коэффициентов. Перед началом вычисления полинома F(x) и а + а„х + а х + ... вх ф аргу- 65 мент Х записан в регистре аргумента 2.

В блоке коэффициентов 10 записаны ковффиыиенты aL,(i= m+1(, которые определяются следующим образом:

I 4щ-,(ке —. О ффф .

1 (фф ф:ф

-о, >

Щф1 (нф ф к1 гне Ск д.— кГ(—., — биноыинеиьные коэффициенты.(При этом каждый коэффициент о ;(=2, н + 1) записан соответсте венно в регистры 6-8, а коэффициент

Ф(записан в регистре 9.

В состав блока коэФФициентов 10 может входить, например, запоминающее устройство, в котором хранятся наборы коэффициентов, соответствующих различньм функциям,;аппроксимнруемих многочленами. Перед нача-. лом вычисления определенного многочлена соответствующие коэффициенты находятся в регистрах коэффициентов.

Вычисление полинома осуществляется следующим образом.

С выходов регистра аргумента 1 значение аргумента Х поступает на входы сумматоров 2-4 и на адресные входы блока постоянной памяти 5. На выходах сумматоров 2-4 образуются соответственно значения (Щ+Х),где

2, m. На выходах блока постоянной памяти 5 формируется значение функции - (х + x + ... + х(ф + x " ).

°

Коды с выходов суюаааторов 2- 4 поступают на адресные входы блоков постоянной памяти 11-13, на выходах каждого i-го из которых (блоку 11 соответствует номер i = 1, а блоку

13 номер i = m ) формируется значение Функции fat; + )()ф . Окончательное значение полинома F(x) формируется в суммирующем блоке 24 пу-, тем суммирования кодов с выходов блоков постоянной памяти 5, 11-13 и кода с выходов регистра коэффициЕнтов 9. Таким образом, на выходах 15 устройства значение полинома формируется в виде

RA q -Мх))44 х)з+ ...+ (а,а+ф х (ф

-(х Жк ... х ) а ар ариф а Xõ

1067509 7л с ьв.л Ь0л

ВНИИПИ Заказ 11210/52 Тираж 699 Подписное

Филиал ППП "Патент"., r.Óæãîðîä, ул.Проектная,4

Как следует из описания работы данного устройства, время вычисления многочлена составляет где t — время возведения в степень; — время суммирования (ш+2)-х кодов в суммирующем блоке.

Как уже отмечалось, блоки возведения в степень и функциональный блок можно построить на основе блоков постоянной памяти. Сравним с задержкой в одноразрядном сумматоре 1 . Например, задержка сигналов в блоке постоянной памяти, пост», роенном на основе микросхем 155PE21,. составляет 60 нс, а задержка в четырехразрядном сумматоре (ликросхема

155ИМЗ) — 55 нс Г92. В зтом случае можно принять t6 = 5 t+. Определнм время t,. При построении суммирУющего блока в виде многослойного сумматора Г101 время сложения в нем (ш+2) чисел составляет (п+2 t og (m+2 ) ) t ° Тогда время вычисления в известнсм устройстве в аз больше времени вычислений в пред® лагаемом устройстве. Здесь принята последовательная организация переносов в сумматорах, временем, пренебрегаем. Напрюлер, для n =. 32, m = 8 получим ръ 16,5. Кроме того, 15 предлагаемое устройство требует для построения меньшего объема памя- ти, чем табличное устройство 53).

Действитель но, общий объе л постоянной памяти в данном случае составЯ ляет при m = 5 и n = 12 величину

6(2" - 12) = 295 К бит. т.е. на

688 - 295=393 К бит меньше, чем в известном устройстве.