Сумматор по модулю 2 @ -1
Иллюстрации
Показать всеРеферат
СУММАТОР ПО МОДУЛЮ 2 - 1, содержащий в.каждом разряде элемент НЕРАВНОЗНАЧНОСТЬ, элемент И и элемент ИЛИ, один из входов которого подключен к выходу элемента И, один из входов которого соединен с выходом элемента НЕРАВНОЗНАЧНОСТЬ, а другой является входом переноса из f S .: ... ,.-,,-.,,.,,J предыдущего разряда сумматора, входы элемента НЕРАВНОЗНАЧНОСТЬ являются входами соответствующего разряда сумматора, а выход элемента ИЛИ является выходом переноса в последующий разряд сумматора, отличающийся тем, что, с целью повышения быстродействия и упрощения сумматора, он содержит в каждом разряде элемент ИЛ11-НЕ и элемент РАВНОЗНАЧНОСТЬ , причем входы элемента ИЛИ-НЕ соединены с соответствующими входами элемента НЕРАВНОЗНАЧНОСТЬ, его выход соединен с другим входом элемента ИЛИ, входы элемента РАВНОЗНАЧНОСТЬ соединены соответственно с выходом элемента НЕРАВНОЗНАЧНОСТЬ (Л и другим входом элемента И, а его выход является выходом соответствую .щего разряда сумматора.
СОЮЗ С08ЕТСНИХ
СОЦИАЛИСТИ, ВЕСКИХ
РЕСПУБЛИК
4(51) G 06 F 7/50
ОПИСАНИЕ ИЗОБРЕТЕНИЯ
H АВТОРСКОМУ СВИДЕТЕЛЬСТВУ.3
ГОСУДАРСТВЕННЫЙ НОМИТЕТ СССР
ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ (21) 3692438/24-24 (22) 19.01.84 (46) 15,05.85. Бюл. В 18 (72) А.И.Карпухин (53) 681.327.66(088.8) (56) 1. Авторское свидетельство СССР
Ф 800992, кл. G 06 Р 7/50, 1981.
2. Савельев A.ß. Арифметические и логические основы цифровых автоматов. M., "Высшая школа", 1980, с. 122 (прототип). (54)(57) СУММАТОР ПО МОДУЛЮ 2 — 1, содержащий в.каждом разряде элемент
НЕРАВНОЗНАЧНОСТЬ, элемент И и элемент ИЛИ, один из входов которого подключен к выходу элемента И, один иэ входов которого соединен с выходом элемента НЕРАВНОЗНАЧНОСТЬ, а другой является входом переноса из
„„SU„„1156063 предыдущего разряда сумматора, входы элемента НЕРАВНОЗНАЧНОСТЬ являются входами соответствующего разряда сумматора, а выход элемента
ИЛИ является выходом переноса в последующий разряд сумматора, о т л ич а ю шийся тем, что, с целью повьпиения быстродействия и упрощения сумматора, он содержит в каждом pasряде элемент КПИ-НЕ и элемент РАВНОЗНАЧНОСТЬ, причем входы элемента
ИЛИ-HE соединены с соответствующими входами элемента НЕРАВНОЗНАЧНОСТЬ; его выход соединен с другим входом элемента ИЛИ, входы элемента РАВНОЗНАЧНОСТЬ соединены соответственно с выходом элемента НЕРАВНОЗНАЧНОСТЬ и другим входом элемента И, à его выход является выходом соответствую,щего разряда сумматора.
11560
Таблица 1
0 1
0
Изобретение относится к вычислительной технике и может быть использовано в устройствах обнаружения и исправления ошибок корректирующими кодами. S
Известен комбинационный двоичный сумматор, содержащий в каждом разряде элементы И и ИЛИ (1) .
Недостаток такого сумматора— его низкое быстродействие при сложении чисел по модулю 2 -1.
Наиболее близким техническим решением к изобретению является сумматор по модулю 2 — 1, содержащий щ одноразрядных сумматоров с целью циклического переноса, каждый из которых содержит два элемента НЕРАВНОЗНАЧНОСТЬ, два элемента И и элемент ИЛИ, входы которого соединены с выходами элементов И,.входы первых 20 элементов И и НЕРАВНОЗНАЧНОСТЬ являются входами сумматора, а входы вторых элементов И и НЕРАВНОЗНАЧНОСТЬ соединены с выходами первого элемента НЕРАВНОЗНАЧНОСТЬ и с входом пере- 2 носа из предыдущего разряда сумматора. Кроме того, сумматор содержит а-разрядный элеменr И и а двухраэ-рядных элементов И, причем входы .а-разрядного элемента И соединены 30 выходами вторых элементов НЕРАВНОЗНАЧНОСТЬ всех одноразрядных сумматогов, а его выход — с первыми входами двухразрядных элементов И, вторые входы которых соединены с выходами элементов НЕРАВНОЗНАЧНОСТЬ соответственно f2) . !едастаток известного сумматора— его малое быстродействие и относительная сложность . 49
Целью изобретения является ïîâûвенке быстродействия и упрощение сумматорв.
Поставленная цель достигается тем, что сумматор по модулю 2 — 1, содер-,ц
Ю жащий в каждом разряде элемент НЕРАВНОЗНАЧНОСТЬ, элемент И и элемент ИЛИ, один из входов которого подключен к выходу элемента И, один из входов которого соединен с выходом элемента щ
НЕРАВНОЗНАЧНОСТЬ, а другой является входом переноса кз предыдущего разряда сумматора, входы элемента НЕРАВНОЗНАЧНОСТЬ являются входами соответствующего разряда сумматора, а выход у элемента ИЛИ является выходом переноса в последующий разряд сумматора, содержит в каждом разряде элемент
63 2
ИЛИ-НЕ и элемент РАВНОЗНАЧНОСТЬ, причем входы элемента ИЛИ-НЕ соединены с соответствующими входами элемента
НЕРАВНОЗНАЧНОСТЬ, а его выход соединен с другим входом элемента ИЛИ, входы элемента РАВНОЗНАЧНОСТЬ соединены соответственно с выходом элемента НЕРАВНОЗНАЧНОСТЬ и другим входом элемента И, à его выход является выходом соответствующего разряда сумматора.
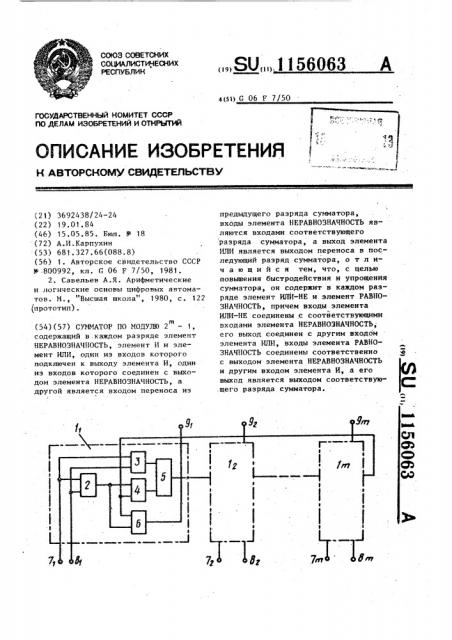
На чертеже изображена блок-схема предложенного сумматора.
Сумматор по модулю 2 — 1 содержит
Ю одноразрядных сумматоров каждый из которых содержит элемент
НЕРАВНОЗНАЧНОСТЬ 2, элемент ИЛИ-!!Е Э, элемент И 4, элемент ИЛИ 5, элемент
РАВНОЗНАЧНОСТЬ 6. Выходы 71-7щ и
8!-8 !„ элементов НЕРАВНОЗНАЧНОСТЬ 2 и ИЛИ-НЕ 3 являются входами соответствующего разряда сумматора. Выход элемента ИЛИ 5 является выходом переноса соответствующего разряда сумматора, а выходы 9 -9> всех элементов
РАВНОЗНАЧНОСТЬ 6 являются выходами сумматора по модулю 2 — 1.
Сумматор по модулю 2 — 1 работает следующим образом.
Заменим сложение по модулю 2 — 1 входных аргументов 4 и б вычитанием:
ja e),.я 5 где 8 — порязрядная инверсия 8
Представим теперь вычитаемое (-3) в отрицательной двоичной системе счисления. Тогда сложение аргумента
А с аргументом (-5) осуществляется. без переноса.
Например, сложим числа 4 101 и
В = 110 по модулю 7.
Инверсия В: В = 001
-В = 001
Слож 4 + (-В): 1О1
+ 001
Действительно, j5+6jg = 4.
Однако в общем случае результат может получиться в двоичной избыточ-, ной системе счисления с цифрами
1, О, 1. Таблица сложения в каждом разряде представлена в табл. 1.
1156063
Т а б л и ц а 2 !
Р; =а;Ъ;ч б Р;, 5 =5. ОР (2) S;
О
1 О О
1 О О
0 1 О
О . 1 О о о
О О 1 .
О
15
О
Отсюда: S. а Ь вЂ” положительная
Ф ч 1 1 26 сумма;
S; а;В; — отрицательная сумма; о
S; а; Ъ; — сумма, равная нулю.
Перевод в обычную двоичную систему счисления осуществляется по табл. 2, откуда Р;*Q qQ. Р. .Q, g P. «ug î Р
1 1-1>
5 6 ЭР,. (1) З0
Для сравнения с двоичным суимато.рои объединии табл. 1 и 2 в табл. 3, где поместим также значения S и Р.
4 для двоичного сумматора.
Таблица 3
Р;, Б; Р; 5, Р (I
0 О О
1 1 О О О
1 О
О 1
О 1
1 О
1 О
1 1 1 О 1
Такии образом, использование
З0 предложенного сумматора по модулю 15 (Ф 4) позволяет сократить время выполнения операции сложения по модулю 15 с однозначным изображением нуля на 160 нс и уменьшить оборудование.
О 1 О
1 О 0
1 1
1 1
ВНИИПИ Заказ 3146/45 Тираж 710 Подписное .
Филиал ППП "Патент", г.ужгород, ул.Проектная, 4
О О О 1 1 О О
О О О 1 1 О
Формулы двоичного сумматора
Из формул (1) и (2) заключаем, что сумматор по модулю 2 — 1 отлиPl чается от двоичного сумматора в каждом 1 -м разряде элементом ИЛИ-НЕ вместо элемента И при формировании переноса и инверсией суммы (элемент РАВНОЗНАЧНОСТЬ вместо элемента НЕРАВ"
НОЗНАЧНОСТЬ).
Следовательно, сумматор по модулю
2 — 1 работает аналогично двоичному сумматору за исключением того, что разрядный перенос при формировании переноса Р образуется при нулевьгх потенциалах на входах 7 и 8 сумматора, а результирующая сумма является инверсной по отношению к двоичному сумматору.
Таким образом, введение элемента
ИЛИ-НК и элемента РАВНОЗНАЧНОСТЬ в сумматор по модулю 2 - 1 позволяет по сравнению с прототипом не применять tn -разрядный элемент И и двухразрядных элементов И, что увеличивает быстродействие сумматора по модулю 2 — 1 и уменьшает его оборудование.
Сравним предложенный сумматор по модулю 2 — 1 при п1 4 (модель 15), построенный на элементах серии 564, с двоичныи сумматором, а именно с микросхемой 564ИМ1 (базовый элемент) ° в.которой выход переноса соединен с входом переноса. Считая предложенный суиматор по модулю 15 по слокности равным базовому объекту, получим: предложенный сумматор содержит одну микросхему 564ИМ1; время выполнения сложения 4 1100 нс; прототип содержит одну микросхему 564ИИ1, 1/2 микросхе- . мы 564ЛА8 и одну микросхему 564ЛА7; время выполнения операции сложения по модулю «< 1260 нс.