Составитель-решатель характеристических уравнений систем автоматического регулирования

Составитель-решатель характеристических уравнений систем автоматического регулирования

Иллюстрации

Показать все

Реферат

 

№ 119009

Класс 42m, 14 ж NBNP®«g п61ВЛрфф11Уфв « ЖИМА

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ

С. А. Гинзбург

СОСТАВ И ТЕЛ Ь- Р Е1ИАТ ЕЛЬ ХАРАКТЕР ИСТИ Ч ЕСК ИХ

УРАВНЕНИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Заявлено 7 октября 1953 r. за № 26082/455997/25 в Чинис ерств > машиностроения СССР

Предметом изооретения является электромеханическое устройство для решения характеристических уравнений систем автоматического регулирования, состоящее из фазовых модуляторов и потенциометров, моделирующих характеристические полиномы структурных звеньев системы автоматического регулирования, следящих систем, с помощью которых отрабатывается напряжение, соответствующее характеристическому полиному всей системы, а также электронно-лучевого индикатора корней полиномов.

Предлагаемое устройство выполняет следующие функции: составляет характеристическое уравнение системы автоматического регулирования по заданным оператором звеньям и структуре системы; определяет корни характеристического уравнения системы; изображает корни на комплексной плоскости.

Предлагаемое устройство отличается от известных тем, что оно дает возможность составлять характеристические полиномы непосредственно по структуре и характеристикам отдельных звеньев системы автоматического регулирования, не прибегая к вычислению коэффициентов характеристического полинома.

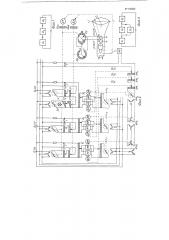
На фиг. 1 представлена структурная схема системы автоматического регулирования без обратной связи из трех звеньев; на фиг. 2 — принципиальная электрическая схема составителя-решателя характеристического уравнения системы автоматического регулирования без обратной связи; на фиг. 3 — схема системы автоматического регулирования с обратной связью; на фиг. 4 — структурная схема составителя-решателя характеристического уравнения системы автоматического регулирования с обратной связью.

Характеристическое уравнение системы автоматического регулирования без обратной связи, состоящей из трех звеньев (фиг. 1), имеет вид: № 119009

D, (z) D (z) D., (z)

К, Ж,.К., где: В (2) gg(z), 0 () — характеристические полиномы звеньев, Кь К, К вЂ” коэффициенты усиления.

Beëè÷èHé "z в общем случае является комплексной и может быть выражена в показательной форме

z. = r, ° e - °

I (2) e - +

/ (s —,. а., + аs) Поэтому характеристические полиномы звеньев также являются комплексными величинами:

D, (z) = Ч е " 2 (z) Ч2 (3) з() =Re"

Следовательно, характеристическое уравнение системы приводится к виду:

Чl 72 ЧЗ > г (4)

Пусть, например, звенья Di и D системы являются инерционными, а звено D — колебательным, тогда:

D, () = Та —, 1= Тое 1" —;1= qе >

D (z) =- Tz+1=- T,oe "- +1= q.,е)"- (5)

D., (z) = T., z —,Т, - =-+ 1 = T, - p e -" + Тре —. 1 = — q,å)"

Моделирование характеристических полиномов звеньев в устройстве (фиг. 2) производится также, как описано в авт. св. № 98013

Аргументы комплексных членов полиномов 2ср и изображаются фазами переменных напряжений, изменяемых с помощью фазовращателей (сельсинов с трехфазными статорами и однофазными моторами).

Фазовращатели приводятся в движение все одновременно от двигателя

Л . Модули комплексных членов полиномов Т,, Т р, T," и Т<," изображаются амплитудами переменных напряжений, изменяемых с помощью потенциометров. При этом постоянные времени Ть Т, Т и Т4 задаются вручную, а величины, и изменяются с помощью потенциометров, движки которых перемещаются все одновременно от двигателя

Л, . Единица моделируется перемснным напряжением постоянной амплитуды.

Решение уравнения основано на методе обследования комплексной плоскости. Обследование осуществляется путем спиральной или радиальной развертки независимой переменной = i> е в комплексной плоскости.

Выходные напряжения схем, моделирующих полиномы, при этом непрерывно изменяются. Эти напряжения необходимо разделить на коэффициенты усиления и перемножить между собой. Коэффициенты

1 1 1 усиления устанавливаются вручную на потенциометрах—

1 2:3

Для перемножения предусмотрены следящие системы, отрабатывающие

Ч Ч Чз модули, —,."-, и аргументы а,, >,,, полученных величин.

1 ( J 3

Для каждого полинома предусмотрены два нуль-органа НА и НФ. НА реагирует только на амплитуду переменного напряжения, НФ вЂ” только на фазу этого напряжения. Эти нуль-органы воздействуют на двигатель амплитуды ДА и двигатель фазы ДФ.

М 119009

Двигатель ДА ведет движок уравновешивающего потенциометра до равновесия, двигатель ДФ поворачивает ротор уравновешивающего фазовращателя до совпадения фаз. Двигатели ДФ поворачивают также роторы фазовращателей ФМИ ФМ, ФМз, из которых ФМ и ФМз представляют собой сельсин-дифференциалы, а ФМз — обычный сельсип.

Сельсин ФМ| питается от сети трехфазного тока, В результате фаза выходного напряжения ФМз равна Ill+ хз — х". ),вигатели ЛА перемещают также движки потенциометров амплитудных модуляторов.

Б результате выходное напряжение АМз составляет

Это напряжение складывается с напряжением, равным единице, и подается на нуль-орган НО. Те значения р и з, при которых срабатыВает нуль-орган, и яВляются корнями .;.арактеристического уравнения системы, Для отсчета значений корней в простейшем случае при срабатывании нуль-органа двигатели останавливаются .. Ве.п. ины и ; отсчитываются по шкалам,"1рг. и Мод.

Для аВтоматического Изображения KopHEll HH Ko_#_ I;ICKcHQII сти применяется электронно-лучевая трубка, экран которой изображает комплексную плоскость. С помощью линейного потенциометра П р, ДВИЖОК KOTOPOrO, ВРашасмЫЙ ДВИГВТЕЛСМ Д;, ЭЛектрИческИ СОЕДИНЕН C синус-KocHHlcHbIM потенциометром П, связанным с дВигателем Д, HB отклоняющие пластины трубки подаются напряжения, сояр и р sill подготавливающие развертку луча по экрану.

В момент срабатывания нуль-органа на сетку трубки подается сигнал, отпирающий луч, и на экране появляется точка, изображающая корень. Путем применения трубки с длительным послесвечением можно наблюдать на экране одновременно несколько корней уравнения.

Характеристическое уравнение системы автоматического регулирования с обратной связью (фиг. 3) имеет вид: (7)

Представляя полиномы звеньев в виде комплексных величин, характеристическое уравнение (7) приводится к виду: (8)

Первый член уравнения в устройстве (фиг. 4) моделируется так, что полиномы при этом располагаются в порядке Dl, .0з, Dz, D4.

Второй член уравнения моделируется путем отбора выходного напряжения с ФМз. Это напряжение пропускается через амплитудные модуЛятОрЫ AlMI И ЛМз, уПраВЛяЕМЫЕ От ОСЕЙ ОтрабОтКИ вЂ” - и — - СЛЕдящих систем СС и ССз.

Третий член уравнения получается путем отбора напряжения от полинома D4(z) после потенциометра для установки коэффициента усиления 1/К4. Напряжения всех трех членов складываются между собой и подаются на нуль-орган. № 119009

Предмет изобретения

Комитет по делам изобретений и открытий при Совете Министров СССР

Редактор Л. A. Блатава Гр. 174

Подп, к печ. 18.И11-59 г.

Тираж 785 Цена 50 коп.

Информационно-,издательский отдел.

Объем 0,34 п. л. Зак. 2909

Типография Комитета по делам изобретений и открытий при Совете Министров СССР

Москва, Петровка, 14.

Составитель-решатель характеристических уравнений систем автоматического регулирования, содержащий фазовые модуляторы и потенциометры для образования и непрерывного изменения аргумента и модуля полиномов от комплексной переменной, значения модуля и аргумента которой, обращающие в нуль характеристический полином, наблюдаются на экране электронно-лучевой трубки или по соответствующим шкалам, отл и ч а ю щи и ся тем, что, с целью ускорения и упрощения анализа систем автоматического регулирования, фазовые модуляторы и потенциометры соединены между собой соответственно операторным выражениям звеньев исследуемой системы автоматического регулирования в отдельные узлы, на выходе которых включены следящие устройства, производящие умножение модулей и сложение аргументов, относящихся к отдельным структурным звеньям системы.