Интегратор для решения дифференциальных уравнений в частных производных

Интегратор для решения дифференциальных уравнений в частных производных

Иллюстрации

Показать все

Реферат

 

_#_î o124553

Класс 42d, 10

42m, 14

СССР

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

К ЗАВИСИМОМУ АВТОРСКОМУ СВИДЕТЕЛЬСТВУ

Л, А, Вулис и А. T. Лукьянов

ИНТЕГРАТОР ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЪНЫХ

УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ

Звявлеио 6 апреля !959 г. в» М 62438it26 в Комитет по лел;1 I ивовретении открытий при Совете Ми. IHcTpoH ГГГР

Оп о: «конвио и «Б оллетене ияооретеиий: X 23 3 !959 г.

Основное ввт. св. Лв !2234! от 25 IIîÿîðÿ !958 г. ив им I теx:гке лии

Изве тные электрические устройства для интегрирования дифференциальных уравнений в частных производны:, с дискретным пространством H временем, конечно-разностным методом (например уравнения типа теплопроводности) выполняются в виде нескольких пар потенциометров, величины потенциалов íà которых имитируют значение функции в выбранных точках области. Счетно-решающий элемент. состоящий из нескольких конденсаторов переменной емкости, поочередно подключает,"я к соответствующим потенциометрам. После олще твления необходимых переключений между конденсаторами счетно-решающего элемента новое значение потенциала, соответствующее значению функции г.ремени, отличающегося от предыдущего на интервал At, переносят с помощью статпческого нуль-инструмента на один из потенциометров, моделирующих задание функции в точках области. Путем последовательного обхода всех пар потенциометров на одной из них появится новое значение функции, соответ;=твующее времени t + At, где t — текущее значение времени. Чтобы продвинуться в решении уравнения е!це на один шаг Ж, полученное распределение потенциала используется для получения последующего значения функции, соответствующего времени

t+2М,и т. д.

В отличие от этого в описываемом интеграторе для решения дифференциальных уравнений в частных производных приращение времени моделируется не емкостями, а омическими сопротивлениями, что позволяет уменьшить ошибку прибора, соответственно повысив точно ть решения уравнений.

Л 124б53

Интегратор состоит из набора потенциометров с высокой разрешающей способностью, счетно-решающего элемента (блока омических сопротивлений) и измерительных приборов. С помощью переключающего устройства счетно-решающий элемент поочередно подключается к оответствуюгцим прхенд ометрам, чем моделируется приращение времени.

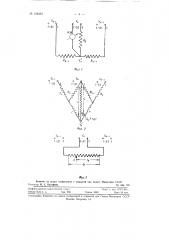
Простой расчет" Йоказывает, что если к трем точкам К вЂ” 1, К, К+1 (фиг. 1) подключить три потенциала V„,, V„V„, имитирующие значение функции V, в соответствующих точках области, то в узле Г„ установится соотношение потенциалов, откечающее уравнению типа теплопроводно,"ти, записанное в конечных разностях следующим ооразом:

V,, t- .i t — 1;, i V„- „ t-: 2 V,,-, t+ V,, t

==- а

Действительно, для точки V справедливо равенство:

V; — V, V,, — V, "— О

Я.-, R„„R„(2) Полагая R,.,=R,„+,â€”вЂ” R, найдем — 1 » — V„-, ()

2 —. r

У где r = R Rp, Падение напряжения на сопротивлении Rp, отнесенное к временному интервалу М, составит

I — 1 V„,— 2 V,- + V<+, (4)

Ь (Ь 1 2

Сравнивая (4) и (1), найдем условия моделирования

an t 1 .х Q y

При заданных а, Лх и r определится значение временного интервала Л1. В процессе решения уравнения на потенциометрах каждой пары получается два значения функции (потенциала) в данной точке, разделенные временным интервалом М.

При решении нелинейного дифференциального уравнения типа (5) с<и>; <и>, — (л г> ( (6) применяется омический элемент (блок сопротивлений), изображенный на фиг. 2. Этот элемент воспроизводит приращение времени для случая зависимости коэффициентов уравнения от функции Результат решений (значение функции У,, 1+ At) при этом получается на сопротивление г„в точке А. Условия моделирования будут: гк Ра 1к

r„ ч где а,.:= —. Сопротивления г постоянны. Однозначно утанавливаС.. ются также соотношения между At, Лх и а, Для упрощения схемы счетно-решающего элемента можно значение V » перенести на один из потенциометров пары К (фиг. 2), а затем используется схема, приведенная на фиг. 3. Beëö÷èíà потенциала точки А потенциометра 1р, соответствующая функции U„, t + 4t переносится на левый потенциометр пары К. № 124Д5Д

Преимущества таких интеграторов определяются простотои измерения (в состоянии равновесия) и возможностью активного вмешатель, тва в процесс решения на любой его стадии. Поэтому такие интеграторы особенно удобны для решения уравнений в частных производных с переменными коэффициентами, зависящими от координат, времени или искомой функции, и задач с источниками и стоками (например задача о диффузии нейтронов и т. п.).

Предмет изобретения

Интегратор для решения дифференциальных уравнений в частных производных по авт. св. № 122341, отличающийся тем, что, с целью уменьшения ошибки интегрирования для моделирования приращения времени, применен блок омических сопротивлений, поочередно соединяемый с потенциометрами, моделирующими пространственное распределение функции.

¹ 124653 пк+т

Фиг 1

Комитет по делам изобретений и открытий при Совете Министров СССР

Редактор Н. С. Кутафина Гр. 166; 174

Типография Комитета по делам изобретений и открытий при Совете Министров СССР

Москва, Петровка, 14.

"и- о

f+df с

$+gt

Информационно-издательский отдел

Объем 034 п, л. Зак. 858 rc+ r о

+dt t

Подп. к печ. 27.IV-60 г.

Тираж 1050 Цена 50 коп.