Способ определения содержания ионов металла в катионите

Способ определения содержания ионов металла в катионите

Иллюстрации

Показать все

Реферат

 

Изобретение относится к области гидрометаллургии и позволяет повысить точность определения содержания металла в катионите при переработке цветных металлов и упростить анализ. Сущность способа заключается в том, что содержание металла определяют по формуле (S2-Si/Sy- -Si), где EX - содержание меди в катионите; Е - содержание меди в моноионной солевой форме, которое составляет 13,196%; Si и 5з - абсолютная набухаемость моноионных водородной и солевой форм катионита, которая определяется как разность объемов сухого катионита и набухшего, соотнесенных к массе; S2 - абсолютная набухаемость смешанной формы катионита. 1 табл.

СОЮЗ СОВЕТСКИХ

СОЦИАЛИСТИЧЕСКИХ

РЕСПУБЛИК

„„SU„„1416906 A 1 (gg 4 G 01 N 30/96

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

К А ВТОРСКОМУ СВИДЕТЕЛЬСТВУ

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР

ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ (21) 4198776/23-26 (22) 09.01.87 (46) 15.08.88. Бюл. № 30 (72) А. В. Шубинок (53) 661.183 (088.8) (56) Полянский Н. Г. и др. Методы исследования ионитов. М.: Химия, 1976, с. 48.

Авторское свидетельство СССР № 163415, кл. G 01 N 30/96, 1963. (54) СПОСОБ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ИОНОВ МЕТАЛЛА В КАТИОНИТЕ (57) Изобретение относится к области гидрометаллургии и позволяет повысить точность определения содержания металла в катионите при переработке цветных металлов и упростить анализ. Сущность способа заключается в том, что содержание металла определяют по формуле E„=E(S — К1/Язв — Si), где Е, — содержание меди в катио Ó3 ните; E — содержание меди в моноионной солевой форме, которое составляет 13,196%;

Si u Sz — абсолютная набухаемость моноионных водородной и солевой форм катионита, которая определяется как разность объемов сухого катионита и набухшего, соотнесенных к массе: S — абсолютная набухаемость смешанной формы катионита. 1 табл.

1416906

Изобретение относится к цветной металлургии, а именно к способам определения содержания ионов металла в катионите в системе аналитического контроля сорбционных процессов.

Цель изобретения — повышение точности определения содержания металла в катионите и упрощение анализа.

Пример. Определение содержания металла в катионите известным и предлагаемым способом.

Образцы набухшего катионита КУ-2 стандартного зернения в водородной форме и смешанной медно-водородной форме с содержанием меди 2,15 — 13,196 мас. Я (моноионная солевая форма) промывали дистиллированной водой, отбирали пробы объемом

0,46 — 1,00 л. Пробы отфильтровывали от избыточной влаги, высушивали в сушильном шкафу при 100 — 105 С в слое толщиной

0,2 — 0,3 см до постоянной массы в течение

1 — 2 ч, затем определяли объем и массу сухих образцов. Для контроля определяли фактическое содержание меди в высушенных образцах путем десорбции меди раствором с содержанием серной кислоты 200 г/л в течение 8 — 12 ч в динамических условиях до полного вымывания ионов металла с последующей промывкой, высушиванием ионита и пересчетом массы десорбированной меди на массу сухого ионита в водородной форме.

Полученные данные использованы для определения степени набухания где g — степень набухания;

Vq — отношение объема набухшего катионита к массе сухого катионита, мл/г;

V, — отношение объема сухого катионита к массе сухого катионита, мл/г, и абсолютной набухаемости = "и с где S — абсолютная набухаемость катионита.

На основании полученных значений g и S рассчитывали теоретическое содержание металла в катионите по известному способу по уравнению

ń= — — — (g — gi)

Е

Ъ. Ч. гдеń— содержание ионов металла в катионите, мас. о;

Š— содержание ионов металла в катионите моноионной солевой формы, мас. il;

gi, дз — степени набухания моноионных водородной и солевой форм катионита соответственно; д — степень набухания смешанной формы катионита, по линейному аналогу известного способа по уравнению

Е„= — — — (S i — 5,), E з где Si u Sz — абсолютная набухаемость моноионных водородной и соле5 вой форм катионита соответственно;

S — абсолютная набухаемость смешанной формы катионита, по предлагаемому способу по уравнению

Е Е(5, ) /

5з

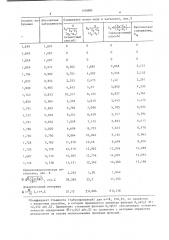
Расчетные значения содержания ионов металла в катионите в сопоставлении с фактическим содержанием приведены в таблице.

Установлены доверительные интервалы, в которых с доверительной вероятностью Р=

=0,95 находится погрешность измерения с верхней и нижней ее границами + A и среднеквадратические отклонения о(Л).

20 Как видно из приведенных результатов, применение линейной функции Е„=ц(5) обеспечивает более высокую точность определенияя (о= 1,38 абс, о ), Как показали результаты испытаний, предлагаемый способ эффективен, прост в осуществлении, отвечает требованиям производства и обеспечивает: повышение точности определения содержания ионов меди в катионите, среднеквадратическое отклонение

30 составляет 1,042 абс. о (17,753 отн.;о) против 2,252 абс. Я (38,35 отн. Я) по известному способу; упрощение анализа за. счет исключения операций в неводных средах и специальной аппаратуры (использование обычного оборудования для измерения

35 объема и массы); сокращение продолжительности определения с 6 — 10 ч до 1 — 2,5 ч и соответствующее повышение производительности сорбционного передела не менее

25 „ (продолжительносгь цикла сорбциядесорбция в промышленной колонке 3 — 6 ч)

Формула изобретения

Способ определения содержания ионов металла в катионите по его набуханию, от45 личаюи ийся тем, что, с целью повышения точности определения и упрощения анализа, измеряют абсолютную набухаемость моноионных и смешанной форм катионита, а содержание ионов металла в катионите смешанной формы рассчитывают по формуле

50 где Е„и Š— содержание металла в катионите смешанной и моноионной форм соответственно;

55 Si и S3 — абсолютная набухаемость моноионных водородной и солевой форм катионита соответственно;

Sz — абсолютная набухаемость смешанной формы катионита. (416906

1,007

1,007

1, 007

1,859

1,859

1,859

0,848

3,533

1, 681

4,903

2,475

1,859 0,971

1,796 0,902

1,42

1,833

1,808

5,23

8, 965

8,816

13, 099

13,091

13,196

Среднеквадратическое отклонение, абс. /

2,252

38,365

1, 042

17,753

1,38

18-1 отн./

23,5,Цоверительный

Д =--- 2 11 X

1S интервал

+ 0,518

+ 0,686

«+1, 12 .Коэффициент Стьюдента (табулированный) для n=18, P=0,95, по сравнению с известным способом, в котором применяется линейная функция Е„=g(e) (G =

=2,252 абс.Ж). Применение степенной функции E„=

1,745

1,800

1,795

1,757

1,781

1,786

1,750

1,728

1, 720

1,687

1, 736

0,954

0,985

0,833

0,904

0,855

0,822

0,854

0,820

0,792

0,783

0,729

0,712

0,738

0,362

5, 701

2,353

4,615

1О,317

5,339

5,792

9,231

7,059

6,606

9,864

11,579

12,579

15,565

11 131

8, 125

4,810

7, 098

8,639

7,145

8,733

10,040

10,46

12,982

13,776

12,562

3,850

6,927

3,443

5,785

5,517

5,835

7,625

9, 1844

9,699

12,926

14,001

12,380

2,151

2,153

2, 261

4,330, 4,364

4,470

6,603

6,594

6,615

8,978