Многофункциональный логический модуль

Многофункциональный логический модуль

Иллюстрации

Показать все

Реферат

 

Изобретение относится к автомат тике и вычислительной технике и может быть использовано для реализации логических функций в рамках системы логического управления. Целью изобретения является расширение функциональных возможностей за счет реализации всех бесповторных логических функций, в т.ч. скобочных, от шести и менее переменных. Многофункциональный модуль имеет раздельные информационные и настроечные входы, содержит элементы И, ИЛИ, РАВНОЗНАЧНОСТЬ . Настроечные сигналы модуля принадлежат множеству О, 1. 1 ил. 1 табл.

СОЮЗ СОВЕТСКИХ

СОЦИАЛИСТИЧЕСКИХ

РЕСПУБЛИК (19) (И) 51 А1 (51)4 G 06 F 7 00

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

И A ВТОРСНОМУ СВИДЕТЕЛЬСТВУ

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР

ПО ДЕЛАМ ИЗОБРЕТЕКИЙ И ОТКРЫТИЙ (21) 4218093/24-24 (22) 31.03.87 (46) 15.10.88. Бюл. № 38 (72) N.Ñ.Астановский, В.Н.Поддубный и О.Ф.Черепов (53) 681.3(088.8) (56) Авторское свидетельство СССР № 643866, кл. С 06 F 7/00, 1976.

Авторское свидетельство СССР

¹ 11227777008866, кл. С 06 F 7/00,,1985. (54) МНОГОФУНКЦИОНАЛЬНЫЙ ЛОГИЧЕСКИЙ

МОДУЛЬ (57) Изобретение относится к автома : тике и вычислительной технике и может быть использовано для реализации логических функций в рамках системы логического управления ° Целью изобретения является расширение функциональных возможностей sa счет реализации всех бесповторных логических функций, в т.ч. скобочных, от шести и менее переменных. Многофункциональный модуль имеет раздельные информационные и настроечные входы, содержит элементы И, ИЛИ, РАВНОЗНАЧНОСТЬ. Настроечные сигналы модуля принадлежат множеству (О, 1). 1 ил.

1 табл.

1430951

Изобретение относится к автоматике, телемеханике и вычислительной технике и предназначено для реализации всех бесповторных логических функций, в том числе скобочных, от шести и менее переменных при равной доступности прямых и инверсных источников информации и возможности перестановки входных переменных, и может быть использовано при построении специальных устройств вычислительной техники.

Цель изобретения — расширение функциональных возможностей модуля за счет реализации всех бесповторных функций, в том числе скобочных, от шести переменных.

На чертеже показан предлагаемый модуль. Модуль содержит входы 1-13, элементы И 14 22, элементы ИЛИ 23-33, элемент РАВНОЗНАЧНОСТЬ 34, выход 35.

Структура модуля. описывается булевой функцией тринадцати переменных

Е .з) = LZZÄ(Z q + Е )(Е ° +

+ Е + Е м)(Е .+ Еа+ ЕУ Е1 )(Е9+

+ Z „0,+ Z«) + ZçZ (Z + z„„)(Z +

Z8)(Z9 + Е о) + Z4Z(,(Е + Е8)(Е9 +

+ 7 0) + ZgZ 8(7.,о+ ZgZ fg) + Е9Е«х

+ (Е1 Е (Е э+ Ей)(Е4+ Е- + Z и)(Е +

+ Еа + 7.7 1„)(Е9 + Z,«.+ Е,g) +

ЕзЕЬ(Е4 + Е )1)(7к+ Еа)(Е 9+ Е ° )+

+ Е,б11х, (Е g+ Еа)(Е 9+ Е«) + Ех.Еах х (Z о+ Z9Z11) + Z9Z « (ZqZ +

+ Z >(Z + 7,1,) + 7

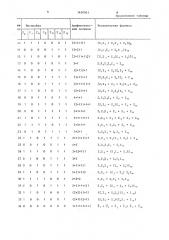
Работа модуля при различных режимах настройки для реализации всех типов бесповторных логических функций от шести переменных описывается таблицей.

I1 р и м е р. Пусть требуется реализовать логическую функцию

5) 1х

Арифметический полином, харак; еризующий тип данной булевой функции, имеет вид (2 + (2 + 1)1. В таб.-тице арифметический полином данного вида определяется номером 26, На информационные входы 1, 2, 3, 4, 5 и 10 подаются сигналы Е,, 7, 7.9, Е, 7, и

7. соответственно, на настрое ейные входы 6, 7„ 8, 12 и 13 н соотв-..тствии с т,;бг.ицеи подается сигнал логическая i, а на настроечные входы

9 и 11 в соответствии с таблицей подается сигнал логический "0", Значение реализуемой функции I снимается с выхода 35 модуля, Аналогично может быть реализована любая бесповторная логическая функция от шести и менее переменных, 2О формула и з о б р е т е н и я

Многофункциональный логи ческий модуль, содержа.;ий девять элементов

И и семь элементов ИЛИ, причем первь."х и второй входы первого элемента И соединены с первым и вторым входами модуля, третий вход которого соедидом четвертого элемента И, первый вход которого соединен с выходом третьего элемента ИЛИ, первый вход которого соединен с выходом пятого элемента И, первый вход которого соецинен с шестым входом модуля, седьмой вход которого соединен с первым входом шестого элемента И„ выход которого соединен с вторым входом первого элемента ИЛИ, третий вход второго элемента ИЛИ соединен с выходом седьмого элемен" à И, первый вход которого соединен с выходом четвертого элемента ИЛИ, первый вход которого соединен с пятым входом мо5О дуля, восьмой вход которого соединен с вторым входом седьмого элемента И, выход первого элемента И соединен с первым входом пятого элемента ИЛИ, выход которого соединен с вторым входом второго элемента И, девятый вход модуля соединен с первыми вхонен с первыми входами второго элеменЗО,та И и первого элемента ИЛИ, выход . которого соединен с первым входом третьего элемента И, второй и третий входы которого соединены с четвертым и пятым входами модуля, а выход

35 третьего элемента И соединен с первым входом второго элемента ИЛИ, вто- рой вход которого соединен с выхо0951

4 версным входом седьмого элемента ИЛИ, вторые входы пятого и девятого элементов ИЛИ соединены с седьмым входом модуля, восьмой вход которого

5 соединен с вторым входом девятого элемента И и первым входом одиннадцатого элемента ИЛИ, выход которого соединен с пятым входом четвертого

10- элемента И, пятый вход второго элемента ИЛИ соединен с выходом второго элемента И, третий вход которого . соединен с вторым входом шестого элемента И и десятым входом модуля, одиннадцатый вход которого соединен с четвертым входом восьмого элемента И, прямым входом седьмого элемента ИЛИ и вторым входом шестого элемента ИЛИ, выход которого соединен с четвертым входом седьмого элемента И, пятый вход которого соединен с вторым входом одиннадцатого элемента ИЛИ и двенадцатым входом модуля, девятый вход которого сое25 динен с вторым входом пятого элемента И, выход девятого элемента И соединен с третьим входом пятого элемента ИЛИ, выход второго элемента

ИЛИ соединен с первым входом элеменЗ0 та РАВНОЗНАЧНОСТЬ, второй вход которого соединен с тринадцатым входом модуля, выход которого соединен с выходом элемента РАВНОЗНАЧНОСТЬ.

Настройка

Арифметический полином

Бесповторная формула

gapa пп

2 1 0 0 0 0 0 1 (2+1)3

3 0 0 0 0 1 0 1 (3+1) 2

4 1 0 0 0 1 0 1 (2+1+1) 2

5 1 1 0 0 0 0 1 (2+2)2 (4+1) 1

I ((2+1) 1+1 J1

8 0 0 1 0 1 0 1 (3+1+1) 1

9 1 0 1 0 0 E (2+1+1+1) 1 з 143 дами шестого элемента ИЛИ и восьмого элемента И, выход которого соединен с четвертым входом второго элемента ИЛИ, выход седьмого элемента

ИЛИ соединен с первым входом девятого элемента И, о т л и ч а ю щ и й— с я тем, что, с целью расширения функциональных возможностей за счет реализации всех бесповторных Функций, в том числе скобочных, от шести переменных, он содержит восьмой, девятый, десятый, одиннадцатый элементы

ИЛИ и элемент РАВНОЗНАЧНОСТЬ, причем третий вход модуля соединен с первым входом восьмого элемента ИЛИ, выход ,которого соединен с третьим входом седьмого элемента И, вторым входом восьмого элемента И и первым входом девятого элемента ИЛИ, выход которого соединен с вторым входом четвертого элемента И, третий и четвертый входы которого соединены соответственно с выходами первого элемента И и десятого элемента ИЛИ, первый и второй входы которого соединены соответственно с выходом шестого элемента ИЛИ и шестым входом модуля, четвертый вход которого соединен с вторым входом четвертого элемента

ИЛИ, выход которого соединен с третьим входом восьмого элемента И и вторым входом третьего элемента ИЛИ, к шестой вход модуля соединен с ин6 7 9 9 Ef 11 !3

1 0 0 0 0 0 0 1.6 0 0 1 0 0 0 1

7 1 0 t 0 0 0 1

1 2 Ф 5 (О (Е,Е + Е„)Е,Е,Z„ (Е» Е Е + Е, ) Е Е о (Е»Ет + Ез + Е ) Е Е о (Е» Е + Е Е ) Е Е (Z»Z2ZзЕ а + Еу)Е о

L (Z,Z + Е )Е + Е5) Е(д (Е„Е Е + ".q + Zs)Z ц (Z Zg + Z + Z + Z )Z

1430951

Продолжение таблицы

Бесповторная формула пп

23 О 1 О 1

241101 (2+2) (1+1) (2+1) (2+1)

1+1+1+1+1+1

Настройка Арифметический полином

7. 7. 7., 7. Е Z

1 О О 0 1 (2+2+1) 1

11 О О О О 1 1 (3+2) 1

12 1 1 0 О 1 О 1 (2+1(1+1)) 1

13 0 О О 1 О 1 1 5+1

14 1 О О 1 0 1 1 (2+1) 2+1

15 О О О f 1 1 1 (3+1) 1+1

16 1 О 0 1 1 1 1 (2+1+1) 1+1

17 1 1 О 1 О 1 1 (2+2) 1+1

18 О О i 1 0 1 1 4+1+1

19 1 0 1 1 О 1 1 (2+1) 1+1+1

20 0 О 1 1 1 1 1 3+1+1+1

21 1 О 1 1 1 1 1 2+1+1+1+1

22 1 1 1 1 О 1 1 2+2+1+1

1 1 1 3+2+1

1 1 1 2+1 (1+1)+1

25 0 О 1,0 0 1 1 4+2

26 1 1 1 О О 1 1 2+(2+1)1

27 0 1 О О 1 1 1 3+3

28 О О 1 О 1 1 1 3+(1+1)1

29 1 1 О О 1 1 .1 2+(1+1)2

30 1 1 1 1 О О 1 2+2+2

31 .1 О 1 О 1 1 1 2+(1+1+1) 1

321101001

33 1 О О. 1 О О 1

340 О О 0 О 0 0 (Е„Е z + ЕзЕ + Zg) Zg (Z„ l zZg + ZpЕ g)Zgp

EZqZ z+ Ез(Е4. + ЕФЕ о

ZgZzZ)Z Z " Z о (Е, Е, + Е,) Е Е + Его (Е1Z ° Е.)Е Е,. (Е1Е + Z3+ Е4)zк+ Е« (ЕЕ +Z,Е„)Е +Е

Z

+ Е )Е + Zg + Е о

Е, Е 2Е 3 + Е а + Е +

ZqZg+. Ез + Zq+ Z5 + Z p

Е1Е,+ Е,Е + Е + Е,.

Z ZzZ s + Е+ - + Е с

+ Z (Z++ Z,) + +Е„

Е Е Е ЗЕа. + Е5Е

Е Ет + (7-7 + Е Е о

Z) ZgZ + Z4Z Z tp

Е Е Е + (Е + 4)Z p

Z,Z,+ (Z,+Z,) ЕЕ„

Е Е + Е Е + Е Е о

Е Е + (Е + Е + 7 )Е о (Zq Z z + ЕЛЕ ) (Z g + Z (о) (Zq Е z + Е y) (Е„7. g + Е, ) Е + Е + Е + Е + Е + Е<о

1430951

Продолжение таблицы

Бесповторная формула

РФ пп

Настройка

Арифметический полином

Е Е y Z!! Еg Zqq Е Zq> (1+1)1+1+1+1 (Z„+ 2, Z>+ Z< + Zz + Z„ (1+1+1) 1+1+1 (Е., + Z + Z )Z + Z + Z (с, (!+!)2+1+1 (Z, + R ) ЕэЕ + Z g + Z(o (1+1) (1+1)+1+1 (Zт + Z ) (Zý + Zo) + Zç + 4 (1+1+1+1) 1+1 (2< + 2< + е э+ Z )Z <+ Z ro ((1+1) 1+1 31+1 ((Z(+ с Z Э + Z4t Z + Z(p (1+1+1)2+1 (Z, + Z + Zэ)Zo Z> + Z« (Z + Е )ЕэЕ Е + Z(o

{1+1) 3+ l (1+1, (1+1) 1+1 (2< + Z>) (Z + 2 ) Z + 2 (о (1+1+1)(1+1)+1 (Е, + Z,,+ zэ,) Е + Е,о ) + Z,, (1+1) (1+2)+! (Z „+ Z ) (Zg + Zg Z ) (1+1+1+1+1)1 (Z! + Z + Z + Zo + Е )Его

47 1 О О 1 О 1 О Г(+1+) !+1+1+1) 1 ((2 „+ Z ) Z э+ Е, ) Е 2 о

480 О 0 1 1 1 О

501101010! (1+1+!)1+1)! ((Z q + Е, + Еэ) Е, + Z g )Z(ц

Г(1*1) 2+111 ((Z „+ Z ) Z ç Z + Z 3 Z „ с(1+1) (1+1)+1)! (Z + Е1) (Z + Z ) + Е 5 ) Z<

I51 О О 1 1 О 1 О (1+1+1+1)2

52 1 О 1 О 1 О ((1+1) 1+1 2

53 О О 1 1 1 1 О (1+1+1)3

54 1 О 1 1 1 О (1+1)4

55 1 1 1 1 О 1 О (1+1) (1+1)2

56 О 1 О 1 1 О (1+1+1) (1+1) 1 57 1 1 О 1 1 1 О {1+1) (2+1)1

58 О О 1 О О 1 О (1+1+1+1) (1+1)

59 1 1 1 О О 1 О (1+1) ((1+1)1+1)

60 О 1 О О 1 1 О (1+1+1)(1+1+1) (Е„+ Е + Е + Z )Z 2® (Е„+ Е )((Е, + Z+)Zz+ Е< ) + Z + Z3)(Z + Z + Z(p) 351000000

371 О О 0 1 О О

38 1 1 О О О О О

390 О 1 О О О 0

41 О О 1 О 1 О О

431 1 1 О О О О

440 О О О 1 1 О

45 1 1 О О 1 О О

460 О О 1 О 1 О! (Е + Ет)Е э+ Еа3Е Е о

1+ + э + 5+ Z ) Z Zà,ЕхЕ(о (Z„+ Z,)(Z, + Z,)Е Е„ (Z i + Z + Z )(Z + Z )Z( (Е + Е ) (Еэй+ + Е )Е (Z + Z + Ез) (Z -+ Z>< ) 1430951

io

Продолжение таблицы рифметичесий полином

Бесповторная формула

Настройка

Z Е Zg Zg (Z, + 2 + Е )(2 2 + Z() + Zq) (Z Z„+ Z q + Z(0) (Z„+ Z ) (Z ° + Z+) (Z z + 2 о) 6i 0 0 1 0 1 1 1 (1+1+1) (2+1)

62 1 1 0 0 1 1 1 (1+1) (2+1+1)

63 1 1 1 1 0 0 1 (1+1) (1+1) (1+1)

64 1 0 1 0 1 1 1 (1+1)(3+1)

65 1 1 0 1 0 0 1 (1+1) (1+1)+2

66 1 0 0 1 0 0 1 (1+1) 1+(1+1) 1 (Е„+ 22) (ЕзЕ Х 5+ К о ) + 4) (Zз + Zp) + Z Z( (2„+ Zq)Z э+ (Z q + Z )Z«

Составитель О.Березикова

Техред M.Õîäàíè÷ Корректор И. Муска

Редактор А.Ревин

Тираж 704 Подписное

ВПИИПИ Государственного комитета СССР по делам изобретений и открытий

ll3035, Москва, Ж-35, Раушская наб., д. 4/5

Заказ 5980

Производственно-полиграфическое предприятие, r. Ужгород, ул. Проектная, 4