Способ определения коэффициента гармоник

Способ определения коэффициента гармоник

Иллюстрации

Показать все

Реферат

 

Изобретение относится к технике измерения коэффициента гармоник сигналов низких частот. Цель изобретения - повышение точности измерения. Достигается это тем, что в качестве опорного используют ступенчатый квазисинусоидальный сигнал, определяют разность между измеренным значением квадрата действующего значения напряжения исследуемого сигнала и суммой квадратов измеренных значений квадрата действующего значения напряжения первой гармоники и постоянной составляющей сигнала, Устройство, осуществляющее способ, содержит преобразователь аналог - код 1, блок 2 управления, блок 3 памяти, измеритель 4 квадрата первой гармоники, измеритель 5 квадрата действующего значения сигнала, измеритель 6 квадрата постоянной составляющей сигнала, вычитатель 7 коэффициента гармоник, 1 ил.

СОЮЗ СОВЕТСКИХ

СОЦИАЛИСТИЧЕСКИХ

РЕСПУБЛИК (5ц5 G 01 R 23/20

ГОСУДАРСТВЕННЫЙ КОМИТЕТ

ПО ИЗОБРЕТЕНИЯМ И ОТКРЫТИЯМ

ПРИ ГКНТ СССР

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ (21) 4397420/21 (22) 15.02.88 (46) 23.02.91, Бюл. М 7 (71) Харьковский институт радиоэлектроники им. акад, M.Ê,ßíãåëÿ (72) В.В.Смеляков, А.И.Алисейко, Б.Н.Гартштейн и В.И.Бармин (53) 621.317,73(088.8) (56) Авторское свидетельство СССР

ЬЬ 779897, кл. G 01 R 23/20, 1980.

Авторское свидетельство СССР

М 1322178, кл, G 01 R 23/20, 1987. (54) СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ГАРМОНИК (57) Изобретение относится к технике измерения коэффициента гармоник сигналов низких частот. Цель изобретения — повыше„„Я „„1629S73 А1 ние точности измерения. Достигается это тем, что в качестве опорного используют ступенчатый квазисинусоидальный сигнал, определяют разность между измеренным значением квадрата действующего значения напряжения исследуемого сигнала и суммой квадратов измеренных значений квадрата действующего значения напряжения первой гармоники и постоянной составляющей сигнала. Устройство, осуществляющее способ, содержит преобразователь аналог— код 1, блок 2 управления, блок 3 памяти, измеритель 4 квадрата первой гармоники, измеритель 5 квадрата действующего значения сигнала, измеритель 6 квадрата постоянной составляющей сигнала, вычитатель 7 коэффициента гармоник, 1 ил.

1629873

g и> .,) ) (5) b1 Ui

Ui — — х г 1

g UiSi) ) 2 — а1 ui и (6) Из (3) и (4) получим

Ur =1 ЬЬЧ, П, 1 (9) 35

2 1

U2 = g Р(ti);

П i=1 (2) Uer = U — 01 — uо, 2 2 2 2, (3) (12) и =1

Изобретение. относится к технике измерения коэффициента гармоник сигналов низких частот.

Цель изобретения — повышение точности измерения.

Способ определения коэффициента гармоник основан на измерении коэффициентов Фурье основной гармоники с использованием запоминающего устройства для хранения значений ступенчатой квазисинусоидальной функции, параметры ступенек которой в точках дискретизации выбираются на основе полученной ниже формулы, связывающей минимальную относительную погрешность измерения коэффициента гармоник с величинами ступенек квазисинусоидальной функции, при этом по параметрам ступенек в точках дискретизации ti и по результатам измерения мгновенных значений сигнала в тех же точках U(ti) вычисляются коэффициенты Фурье основной гармоники, квадрат действующего значения этой гармоники, квадрат действующего значения вcего сигнала, квадрат постоянной составляющей, квадрат действующего значения высших гармоник и коэффициент гармоник.. Определим погрешность, вызванную неточным заданием значений тригонометрических функций slnti u costi при вычислении интегральных характеристик, Пусть С1 и

Ci, Si и Sl — точные и приближенные значения косинуса и синуса в точках дискретизации, а ACi = С вЂ” Сь Л Si = Si — Si — их погрешности, Запишем формулы для вычисления интегральных характеристик периодических сигналов:

U,=- ((- g@ñ ) +(2 g и,д) ). (4) Найдем линейное приближение для погрешностей: — Ui Ci +

1 и 2 2

-(-. и) аС4 а дЕ д5 1 и, 2 ,с x ((-„ и,с, +(- а 0вг

2 г

su„=y. лс+ g ës ай„ =1 а rl Si

20 2

= — — „ (а; ACi+ bi Asi) U;. (7)

nI =1

Введем обозначение

Vi = 0 -(a 1COSti + b1Slnti) — Uo, (8) где Ui — мгновенное значение сигнала в точках ti;

uo — постоянная составляющая сигнала; (а1соэ + b1sinti) — первая гармоника сигнала, Можно показать справедливость равенства

Точные значения синуса Si распределены по периоду следующим образом:

S1 S2 " Зп/4 Sn/4-1 " 51, So, (10)

40 — S1, -S2, " $п/4и -Sn/4-1,.", 1, So.

Можно составить подобное распределение по периоду для точных значений коунуса Сь приближенных значений синуса

Si, приближенных значений косинуса Ci u

45 распределения погрешностей Л Si и Л Ci no синусу и косинусу. Например, распределение погрешностей по периоду для синуса записывается в следующей последовательности:

50 ASn/4, ЛЪ/4-1, „„AS1 A So, AS1, — Л S2, „„-Л $п/4-1, — Л Яп/4, (11)

ЛSп/4, ЛSп/4 — 1, ..., AS1, A So, ЛS1

ЛSZ, ..., Л Яп/4-1, Л Sn/4

Легко показать, что для величин ACi, 55 AS;, Ci, Si справедливы соотношения

1629873 (13) (14)

5 (15) 10

Из (5) — (16) получим (23) (17) 20

Оценим второе слагаемое в (17).

Используя неравенство Коши, получим — I g (а1AC>+biASilVit < (— g 4 ) и п1=1 " 25 к (b Õ (а Aci+b>лв ) 7 : и8) g (àq b,Ci+Ь1ЬSi) =(аq +Ьq )

ll г г 30

i =1

Д, ЛЯ =2 U>, AS (19)

1=1 1— = 1

Используя (19), перепишем (18);

35 Следовательно можно записать

Sl = Sip +qm1, где q=2Р;

40 mi =. (20) Для нахождения правила. определения величины ступенек квазисинусоидальной

45 функции необходимо найти такой набор коэффициентов ml(i = 1,2,...,пг), при котором д К достигает минимума. Поскольку общее число различных комбинаций m равно 2 "2, то в большинстве случаев эту оптимизационную задачу не представляется решить путем прямого перебора. Для решения этой задачи используется метод (случайного поиска) Монте-Карло. При этом на одной итерации j значения коэффициентов п ь равные нулю или единице, выбираются случайно, после чего вычисляются значения д K(m

J ) значения ступенек квазисинусоидальной функции, которые установились после пополучим лс с = f лг s,;

1=1 i=1 и п

g ЛС Ю(= g ЛЯ Ci=O

l =1 i =1

ВАЛС г= 2лаг, (=1 ) =1 лс лг,=о. п Ц 2I = I4 0„2 Д5, + и

2 п

+ —, >, (а1ЛCl + bl ЛSl)VjI . и, I AUsr 1 (2 (2 U> (g ЛЯ! Si I—

i=1 и

+ 2@,Ui (— g ASi ) Учитывая, что относительная погрешность коэффициента гармоник определяется соотношением

2 д К=, (21)

=2 0,2

ЛК= — (-,ля, ) 2 1 г 1Л2 п,, + —, („ i g лг, s )) . 1221

Из (22) видно, что относительная погрешность коэффициента гармоник определяется, главным образом, вторым слагаемым. Следовательно, нужно стремиться к уменьшению величин ЛSь чтобы п уменьшить величину g Л SlSl тем самым

1=1 уменьшить количество разрядов запоминающего устройства величин Cl u Si. Поскольи л ку значения Sl на интервалах (О, — ), —,ж), (л, — 2), (, 2л) повторяются, то выражеЗл Зл ние (22) можно записать в виде

1 2 2 3 г 1Л2

1 8 п2

+ — — gAsrS;(, К2п и Il где п1= —; n2 = — — 1; ЛЯ = Я вЂ” Si;

4 4

Яс1 = 00 ... 0; Sni = 11 ... 1; A SU = ЛЯи = О.

Пусть в двоичной системе точное значение синуса представлено в виде . и = О, у, yI2.... yl(P + q, При симметричном округлении величины Si до ближайшего числа на р разрядной сетке округленное значение определяется из соотношения

Sl = Sip=0, p) p2, ° ° °,pp, если1 (Р+ 1) =0; 2 = S р = 0,$ $, 1 12 ...., 1 р + 2 если щр+ 1)= 1, 1 при округлении с избытком, О при округлении с недостатком

1629873 вк=, „— ль )

1 2 2 А g lг — —, ASiSi !.

1 8 З 2п где и — число точек дискретизации эа период, ni = —; nz = — — 1; Л Si = Si — Si, и и

4 . 4

So = 000...0; Я ) = 111 ... 1; ЛЯ<, = Л S = О. д К вЂ” относительная погрешность измерения коэффициента гармоник К;

Si — точное значение ступенек сигнала в точках дискретизации;

Si — приближенное значение ступенек сигнала в точках дискретизации.

Составитель А.Дворников

Редактор И.Шмакова Техред М.Моргентал Корректор С.Шекмар

Заказ 437 Тираж 420 Подписное

ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ СССР

113035, Москва, Ж-35, Раушская наб., 4/5

Производственно-издательский комбинат "Патент", г. Ужгород, ул.Гагарина, 101 следней итерации, фиксируются запоминающим устройством. Эти значения близки к оптимальным, поскольку этому распределению параметров ступенек соответствует наименьшая погрешность, Зная оптимальное 5 распределение памяти, полученное на последней итерации, можно определить q опл г тимальные значения Usr, U< и коэффициента гармоник.

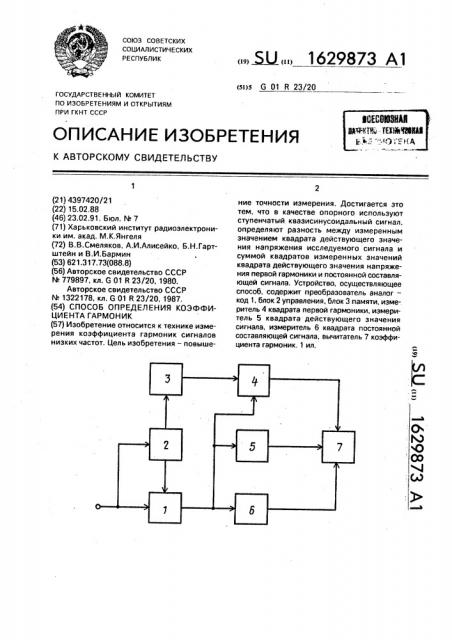
На чертеже представлена блок-схема 10 устройства, реализующего предлагаемый способ.

Устройство содержит преобразователь

1 аналог — код, блок 2 управления, блок 3 памяти, измеритель 4 квадрата первой гар- 15 моники, измеритель 5 квадрата действующего значения сигнала, измеритель б квадрата постоянной составляющей сигнала и вычислитель 7 коэффициента гармоник.

Определение коэффициента гармоник производится следующим образом.

Исследуемый сигнал 0(1) поступает на входы блоков 1 и 2. С выхода блока 1 коды мгновенных значений сигнала U(t ) поступа- 25 ют на вход блоков вычисления квадрата действующего значения первой гармоники, квадрата действующего значения сигнала и квадрата постоянной составляющей. С выхода блоков 4 — б коды квадратов указанных 30 величин поступают в вычислительный блок

7 для определения коэффициента гармоник.

Таким образом, предлагаемый способ позволяет повысить точность измерения коэффициента гармоник при сохранении 35 разрядности цифрового вычислительного устройства и уменьшить время измерения до двух периодов исследуемого сигнала.

Формула изобретения

Способ определения коэффициента 40 гармоник, основанный на измерении коэффициентов Фурье основной гармоники, при котором формируют опорный сигнал, аппроксимирующий исследуемый с п ступеньками на период, моменты переключения которых задают равномерно, а значения ступенек формируют в зависимости от измеряемых мгновенных значений исследуемого сигнала и определяют квадрат действующего напряжения исследуемого сигнала, о тл и ч а ю шийся тем, что, с целью повышения точности измерений, в качестве опорного используют ступенчатый квазисинусоидальный сигнал, определяют разность между измеренным значением квадрата действующвго значения напряжения исследуемого сигнала и суммой квадратов измеренных значений квадрата действующего значения напряжения первой гармоники и постоянной составляющей сигнала, при этом величины ступенек определяются по формуле