Демонстрационная модель кристалла

Демонстрационная модель кристалла

Иллюстрации

Показать все

Реферат

 

Изобретение предназначено для моделирования кристаллов различной формы и может быть, в частности, использовано в системе обучения в качестве наглядного пособия Модель исходного куба выполнена из плотного листового материала, например картона Грани куба разделены линиями связи на субграни, которые благодаря эластичности линий связи могут изменять положение в пространстве друг относительно друга, что придает модели свойство пластической деформации Получение фигур кристаллов различной формы обеспечивается нажатием на определенные линии связи и/или точки пересечения между ними, в результате чего исходная модель преобразуется в ту или иную требуемую форму 4зп ф-лы, 11 ил

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

К ПАТЕНТУ

Комитет Российской Федерации по патептам и товарттьтм знакам (21) 4705612/12 (22) 06.04.89 (46) 15.1293 Бюл. Na 45-46 (71) Ассоциация "Космонавтика — Человечеству" (72) Чепижный К.И. (73) Ассоциация "Космонавтика — Человечеству" (54) ДЕМОНСТРАЦИОННАЯ МОДЕЛЬ КРИСТАЛЛА (57) Изобретение предназначено для моделирования кристаллов различной формы и может быть. в частности, использовано в системе обучения в качестве наглядного пособия. Модель исходного ку(i>) RU (1ц 2004935 С1 (>) ба выполнена из плотного листового материала. например картона. Грани куба разделены линиями связи на субграни, которые благодаря эластичности линий связи могут изменять положение в пространстве друг относительно друга, что придает модели свойство пластической деформации. Получение фигур кристаллов различной формы обеспечивается нажатием на определенные линии связи и/или точки пересечения между ними, в результате чего исходная модель преобразуется в ту или иную требуемую форму. 4 зп. ф-лы, 11 ил.

2004935

Изобретение относится к наглядным пособиям, преимущественно в кристаллографии, и может быть использовано для моделирования блочного строения и процессов пластической и упругой деформации квазисимметричных кристаллов различной формы.

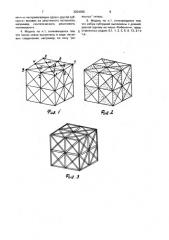
Целью изобретения является придание свойств пластической деформации модели для получения различных по форме фигур кристаллов, а также повышение эстетического изображения и получение возможности описания рекуррентных фигур, На фиг,1 представлена модель исходного гомологического куба; на фиг.2 — 11 — примеры, иллюстрирующие получение различных видов моделей кристаллов, Получение модели исходного куба (фиг.1) осуществляется следующим образом.

Исходным материалом является тонкий плотный лист картона, пластмассы или тому подобного материала, на котором размечают развертку (условно не показана) модели куба. На гранях развертки куба для получения различного вида фигур выполняют ли-Hw связи, которые делят грани куба на субграни, после чего развертку вырезают.

На фиг.1 на грани 1-3-5-7 линии 1-3, 2-6, 2-8, 3-7, 4-2, 4-8. 4-6, 6-8 представляют собой линии связи между соответствующими субгранями со связанными с ними субблоками (субкубами), если рассматривать модель в объемном изображении (фиг.3). Так, напри мер, линия связи 2-6 является линией между субгранями 2-6-7-1 и 2-6-5-3, линия 2-8 является линией связи между субгранями 2-8-1 и 2-13-8, линия 1-9 является линией связи между субгрвнями 1-9-8 и 1-9-2. Линии связи типа 1-3, 3-5, 5-7 и 7-1 являются одновременно ребрами фигуры. Количество субграней определяется законом бесконечности размножения граней. Закономерность (закон) размножения субграней в квазисимметричном кубе геометрически строго показана на фиг,6. Исходная модель куба на фиг,1 содержит восемь субблоков (субкубов). Для обеспечения подвижности граней и субграней друг относительно друга листовой материал многократно перегибают по линиям связи и ребрам граней, которые также являются линиями связи, в обе стороны, получая при этом эластичное (гибкое) соединение между субгранями. В других вариантах выполнения в качестве линий связи между гранями и субгранями можно использовать вставки иэ эластичного материала (плотной ткани, резиновой ленты и

10 т,д,) или петлевые соединения (варианты выполнения условно не показаны) или тому подобные соединения. После образования соединений развертку собирают в куб. соединяя грани склеиванием или при помощи вышеописанных средств. На исходной модели куба (фиг.1) цифрами 1, 3, 5, 7 обозначены вершины куба, в которые выходят тройные оси гомологии, Цифрами 2, 4, 6, 8 обозначены точки, в которые выходят оси гомологии второго порядка. Цифрами 9, 10, 11, 12 обозначены точки выхода осей гомологии четвертого порядка субграней (субблоков), Цифрой 13 обозначена центральная точка, в которой выходит четвертая ось гомологии куба, Следует отметить, что в гомологическом

2р (квазисимметричном) кубе все оси гомологии и ребра являются линиями связи.

Получение различных фигур обеспечивается деформацией исходной модели куба, для чего в простейшем варианте достаточно

25 легкого нажатия пальцами на определенные линии связи и/или точки пересечения между ними, После приложения усилия исходная модель преобразуется в ту или иную требуемую фигуру, При построении моделей, из эстетических соображений, а также для того, чтобы ввести число (меру), длину ребер (линий связи) субграней фигур принимают равной од35 ному из чисел Фибоначчи, представленных рядом;О, 1,1,2,3,5,8, 13,21 ит.д. В этом случае совокупность субграней, вынесенных из грани при моделировании какой-либо фигуры кристалла, может быть описана

40 на основе рекуррентных рядов, так как их размеры закономерно связаны с размерами исходного куба, В связи с тем, что с рядом чисел Фибоначчи связано бесконечное число рекуррентных рядом, появляется воз45 можность описания бесконечно большого количества фигур (кристаллов), Кроме того, при выполнении субблоков с указанным соотношением ребер, осуществляется наиболее естественная их укладка в совокупную

50 структуру с минимальными "зазорами" между блоков, Пример 1. На фиг.2 показана модель кваэисимметричного куба со "ступеньками роста" (перекрытиями), выделенными черными точками.

Пример 2, На фиг.3 представлена модель квазисимметричного куба с двойными плоскостями, описывающими разбиение куба на субблоки и связанные с ними су6 рани.

2004935 (56) Проспект нКристаллографические модели". Л,; 1975, с.22-23.

Формула изобретения многогранника разделены на субграни лик ниями связи, обеспечивающими возможДРМЦНСТРАЦИДННАД МОДУЛ 55кность изменениЯ положениЯ сУбгРаней одКРИСТАЛЛА, выполненная в виде полого на относительно другой в пространстве. многогранника из картона или тому подо- 2, Модель по п.1. отличающаяся тем, бного материала, отличающаяся тем, что, с что линии связи выполнены в виде сгибов целью придания. свойств пластической де- материала граней. формации модели для получения различ- 3, Модель по п.1. отличающаяся тем, ных по форме фигур кристаллов, грани что линии связи выполнены в виде закрепПример 3. На фиг.4 приведена модель двойного квазисимметричного куба Томпсона, полученная после деформации модели на фиг.1. Для этого достаточно легкого нажатия пальцами в четырех точках типа точек 2 и 6, лежащих в плоскости, проходящей через точки 2-6 и центр куба.

Пример 4. На фиг.5 показана модель квазисимметричного звездчатого октаэдра. полученная путем сжатия куба (фиг.1) по шести осям гомологии второго порядка.

Пример 5. На фиг 6 представлена схема размножения линий связи между субгранями квазисимметричного куба (фиг.1). В ряде случаев требуется получить более полную картину о деталях и закономерностях строения кристалла (модели) при заданной деформации. В этих случаях производят

"размножение" линий на гранях фигуры.

Каждую линию можно продолжить. в обе стороны или провести параллельные линии до получения равномерного разбиения граней куба. Из фиг,6 следует, что шестиугольник, обозначенный на фиг,7 цифрами 1-2-3-4-5-6, вращаясь, превращается во все меньший шестиугольник, причем вершина 1 исходного шестиугольника, двигаясь по полигональной cllирали, последовательно (фиг.6) занимает позиции 1, 1, 1 и т,д. Это позво1 III ля ет вы разить спиральное строение грани куба (фиг.8). Такие полигональные спирали, организованные на основе линий (спирали), наносятся на всех гранях куба. При наблюдении со стороны осей гомологии четвертого порядка спирали читаются как четырехзаходные, со стороны тройной оси— как трехзаходные, со стороны двойных осей — как двухзаходные. На фиг.7 размер ребер субграней (субкубов) принят равным 2 см. В этом случае совокупность субграней, вынесенных из грани, показанной на фиг.б, и представленных на фиг.9, может быть описана на основе рекуррентных рядов, так как их размеры закономерно связаны с размерами исходного куба со сторонами субграней (субкубов), равными 2 см.

П р» м е р 6. На фиг.10 представлена исходная модель гомологического (квазисимметричного) кристалла тригонального облика, построенного на основе трех шестиугольников типа, показанного на фиг.7. На модели линии 1-4, 2-5, 3-6, 6-2, 5-3 являются линиями связи. Все точки пересечения линий являются точками кручения. Для того, чтобы придать кристаллу способность к де, формации кручения, следует всем трем граням (шестиугольникам) придать степени свободы, разрешаемые линиями 6-2, 5-3, 25, 3-6. Модель подвергают деформации кручения таким образом, чтобы три точки, типа точки, обозначенной буквой нО", слились в одну точку (образование точки-точек). На фиг.11 приведен результат кручения модели (фиг.f0) по аналогии вращения винта в левую сторону. Как видно из фиг.11, после кручения исходная модель преобразова20 лась в две скрученные бипирамиды. Эта модель демонстрирует механизм кручения, например, природных кристаллов кварца, Как видно из модели, такое кручение осуществляется через октаэдр с ребрами типа ребер 6-2 и 2-3. При построении моделей кристаллов других форм грани куба и их субграни могут подвергаться однородным деформациям растяжения, сжатия. сдвига.

На основе таких граней могут быть построены кристаллы любых других форм, Подвергая, например, квазисимметричный куб однородным деформациям сжатия, его можно преобразовать в квазисимметричный

35 тетраэдр — простейшую из мыслимых замкнутых фигур.

Создание модели с универсальными свойствами пластической деформации обеспечило возможность демонстрации од40 ной исходной моделью множества видов деформаций кристаллов (сдвиги, сжатие, кручение, растяжение и т.д.) и повысило наглядность построения и форм демонстриру45 емых кристаллов.

2004935 ленных на прилегающих одна к другои субг анях вставок из эластичного материала,, например, синтетического, р езинового, тканевидного.

4, Модель по п.1, отличающаяся тем, что линии связи выполнены д в ви е петлевых соединений, например, по типу "рояльных петель

5. Модель по п.1, отличающаяся тем, что ребра субграней выполнены с длиной, равной одному из чисел Фибоначчи, пред5 ставленных рядом: 0,1, 1, 2, 3, 5,,13,21и т.д, 2004935

2004935 составитель У.Чепижный

Редактор В.Трубченко Техред M.Ìîðråíòàë Корректор С. Лисина

Заказ 3397

Тираж Подписное

НПО "Поиск" Роспатента

11 035, Москва, Ж-35, Раушская наб., 4/5

Производственно-издательский комбинат "Патент", г, Ужгород, yn,Гагарина, 101