Способ и устройство быстрого вычисления дискретного вейвлет-преобразования сигнала с произвольным шагом дискретизации масштабных коэффициентов

Способ и устройство быстрого вычисления дискретного вейвлет-преобразования сигнала с произвольным шагом дискретизации масштабных коэффициентов

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области вычислительной техники и может быть использовано для обработки и анализа сигналов самой разнообразной природы (в области связи, радиолокации, гидроакустики, речи, музыки и т.д.).

Термин "вейвлет" (wavelet), появившийся в научной литературе в середине 80-х годов, подразумевает семейство специальных осциллирующих функций с коротким носителем особого вида, используемых в качестве базиса в вейвлет-преобразовании [1-7].

За полтора последних десятилетия теория вейвлет-преобразования (ВП) претерпела бурное развитие и получила исключительно широкое применение в самых разнообразных областях науки (математике, физике, радиотехнике, медицине, биологии и т.д.) [3-5]. В настоящее время вейвлеты стали необходимым математическим инструментом в самых разнообразных исследованиях, особенно в случае, когда результат анализа сигнала должен содержать не просто перечисление его характерных частотных составляющих (или масштабов), но и сведения о локальных координатах, при которых эти частоты себя проявляют. Основным полем применения непрерывных вейвлет-методов в настоящее время стали анализ и обработка нестационарных (во времени) или неоднородных (в пространстве) сигналов различных типов, при решении задач локализации и классификации особых точек сигнала, вычисления его характерных фрактальных характеристик, частотно-временного анализа нестационарных сигналов.

Непрерывное ВП можно определить как скалярное произведение исследуемого сигнала s(t) и базисных функций :

где черта сверху обозначает операцию комплексного сопряжения.

Общий принцип построения базиса ВП состоит в использовании масштабных преобразований с параметром сжатия α и смещений с параметром сдвига τ исходной вейвлет-функции (т.н. материнского вейвлета) ψ (t):

Чтобы быть вейвлетом, базисные функции должны обладать рядом необходимых свойств [1, 3, 6]. Они должны быть: квадратично-интегрируемыми, знакопеременными (и обладать нулевым средним), вейвлеты должны стремиться к нулю на ± ∞ , и для практических целей - чем быстрее, тем лучше (причем вейвлет должен быть хорошо локализован и во времени, и по частоте). Для того чтобы было возможно обратное ВП, функция вейвлета ψ (t) должна удовлетворять еще одному условию:

В настоящее время применяется огромное количество различных семейств вейвлетов (Хаара, Добеши, Морле, FHAT, МНАТ и т.д. [1-6]). Выбор типа анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из сигнала. Каждый вейвлет имеет свои характерные особенности во временном и частотном пространстве. С помощью различных типов вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала. Второй аспект при выборе вейвлета (важный для дискретной цифровой реализации) - это необходимые скорость и объемы вычислений. В этом аспекте наиболее простым (требующим минимума операций перемножения) является преобразование на основе вейвлета Хаара.

Вейвлет-спектр Ws(α , τ ) одномерного сигнала s(t), полученный в результате ВП, является двухмерной функцией и представляет собой поверхность в трехмерном пространстве. При анализе результатов вместо изображения поверхностей часто рассматривают их проекции на плоскость (α , τ ) с изолиниями, позволяющими проследить изменение амплитуд ВП на разных масштабах и в различные моменты времени. Способы визуализации этой информации в плоском случае могут быть различны - цвет, яркость или изолинии. В тех случаях, когда нужно показать очень широкий диапазон масштабов, применяют логарифмические координаты для коэффициента сжатия (log α , τ ).

Интерес для обработки сигналов представляет дискретный вариант ВП [1, 2, 4-7]. Необходимая дискретизация значений α и τ , при сохранении возможности восстановления сигнала из его преобразования, должна осуществляться следующим образом:

Т.е. временной параметр местоположения τ зависит от параметра масштаба α . С увеличением масштаба увеличивается и размер шага сдвига. Для дискретных значений α и τ , при τ ₀=1 (соответствующим сдвигу на один отсчет) вейвлет-функции представляются в виде:

При некотором, весьма специфичном, выборе вейвлета ψ и исходных значений α ₀, τ ₀ дискретный набор функций образуют ортонормированный базис в гильбертовом пространстве. В частности, обычно, без потери общности, выбирают α ₀=2 и τ ₀=1:

Для данного способа дискретизации параметров сжатия и сдвига на основе теории кратномасштабного анализа [1, 2] и аппарата нестандартного матричного умножения созданы все ныне существующие быстрые и эффективные методы вычислений ВП на основе т.н. алгоритма Малла (Mallat) [1, 2, 4, 5, 7] (аналоги). По сути, эти же методы вычисления, в цифровой обработке сигналов называются методами субполосной фильтрации с прореживанием (аналог) [1 (с.221-231), 5].

В целом ряде случаев (например, при анализе экспериментальных данных в физике, обработке сигналов в гидро- или сейсмоакустике, радиолокации и т.д.) нет необходимости жесткого требования существования обратного ВП, но есть требования к произвольно мелкому шагу дискретизации (точнее произвольному основанию 1<a<2 логарифмического шага дискретизации α _m=a^m, m=0,1,... M-1) масштабных коэффициентов и одновременно к быстродействию метода вычислений. Как уже говорилось выше, минимальный дискретный шаг для коэффициента сжатия в современных быстрых и эффективных способах вычисления дискретного ВП равен 2 (α _m=2^m), что соответствует целой октаве в частотной области. В большинстве случаев такая точность измерения масштаба не приемлема для задач анализа сигналов.

Поэтому, в случае необходимости проведения более подробного "непрерывного" (избыточного дискретного) вейвлет-анализа сигнала, обычно применяют традиционный классический способ вычисления ВП во временной области на основе выражения (1) для непрерывного ВП, дискретный вариант вычисления которого [1 (с.31-39), 5] (аналог) требует использования большого количества масштабирующих операций (сжатия) и, соответственно, такого же количества интерполяционных процедур.

Избыточный дискретный вейвлет-спектр (представляющий матрицу вейвлет-коэффициентов размером М× N) для входного анализируемого сигнала длиной N отсчетов в данном способе получается в результате вычисления М взаимокорреляционных функций для предварительно оцифрованного анализируемого сигнала и М предварительно сжатых копий исходного (материнского) вейвлета (значение числа М зависит от заданного шага дискретизации для масштабного коэффициента и максимального коэффициента сжатия a^M-1). Чем меньше шаг дискретизации и больше требуемый диапазон масштабов (частот), тем больше требуется масштабирующих операций (сжатия).

Данный способ (аналог) вычисления "непрерывного" (точнее, избыточного дискретного ВП) может быть реализован одним из вариантов устройств-аналогов.

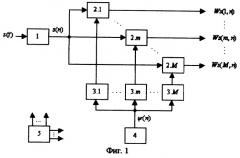
Устройство (аналог), реализующее вышеописанный способ (аналог), приведено на фиг.1, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блоки 2.1 - 2.М - вычислители взаимокорреляционной функции (ВКФ),

блоки 3.1 - 3.М - масштабирующие устройства с коэффициентами сжатия,

блок 4 - постоянное запоминающее устройство,

блок 5 - устройство управления.

Принцип действия устройства заключается в следующем. Анализируемый сигнал s(t) поступает на АЦП (блок 1), с выхода которого дискретная выборка s(n) длиной N отсчетов поступает одновременно на первые входы M вычислителей ВКФ (блоки 2.1 - 2.М).

Из ПЗУ (блок 4) дискретная выборка "материнского" вейвлета ψ ₀(n) одновременно поступает на входы М масштабирующих устройств (блоки 3.1 - 3.М) с коэффициентами сжатия α _m=a^m (Основание a может выбираться произвольно в зависимости от требуемого значения логарифмического шага дискретизации коэффициентов масштаба α ). Промасштабированные версии вейвлет-функций ψ _m(n) поступают на вторые входы М вычислителей ВКФ (блоки 2.1 - 2.М).

С выходов М вычислителей ВКФ (блоки 2.1 - 2.М) снимаются результаты вейвлет-преобразования в виде массива значений вейвлет-коэффициентов размером М масштабов на N сдвигов Wψ {s}(m,n)=Wψ {s}(α _m,τ _n).

Для реализации данного метода вычисления дискретного избыточного ВП с произвольным дискретным шагом масштаба требуется:

- М операций масштабирования (сжатия) исходного вейвлета (и, соответственно, столько же интерполяционных процедур),

- М операций вычисления свертки (соответственно, М· N² операций умножения).

Оператор (1) непрерывного ВП сигнала s(t) может быть определен и в частотной области [1 (с.59, 67-68)]:

где Ψ (f) - образ Фурье выбранного исходного вейвлета ψ (t).

S(f) - образ Фурье анализируемого сигнала s(t).

Единственным ограничением для данной формы записи непрерывного ВП по сравнению с (1) является требование аналитичности для исследуемого сигнала и применяемого вейвлета [1 (с.67-68)]:

suppS(f)⊂ [0,∞ ); suppΨ (f)⊂ [0,∞ ),

т.е. S(f)=0 и Ψ (f)=0 при f≤ 0.

В случае вейвлет-анализа действительных сигналов (что имеет место при обработке радиолокационных, гидролокационных сигналов и т.д.) их легко представить в аналитическом виде, без потери информации, путем обнуления отрицательных частот их комплексных спектров Фурье. То же самое касается и используемых вейвлетов. Причем часть широко применяемых комплексных вейвлетов (например, Морле) сами являются аналитическими сигналами.

В этом случае удобнее использовать способ вычисления непрерывного ВП в частотной области на основе выражения (5) [1 (с.68)] (прототип), дискретный вариант которого также требует использования большого количества масштабирующих операций (сжатия) над спектром исходного вейвлета и, соответственно, такого же количества интерполяционных процедур. В прототипе [1 (с.68)] в качестве вейвлета выбрана функция вида:

Ψ (f)=2fe^-f при f≥ 0; Ψ (f)=0 при f≤ 0,

что непринципиально для записи общего вида оператора ВП (5).

Избыточный дискретный вейвлет-спектр (матрица вейвлет-коэффициентов М× N) для входного анализируемого сигнала длиной N отсчетов в данном способе получается путем вычисления М обратных преобразований Фурье от произведения спектров предварительно оцифрованного анализируемого аналитического сигнала и М предварительно сжатых копий аналитических спектров исходного (материнского) вейвлета.

Спектр выбранного материнского вейвлета должен быть промасштабирован М раз (значение числа М зависит от выбранного логарифмического шага дискретизации для масштабного коэффициента и его заданного максимального значения а^M). Чем мельче шаг и больше требуемый диапазон масштабов, тем больше требуется операций сжатия и масштабирующих устройств.

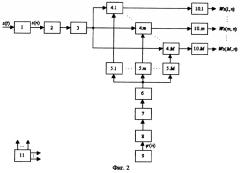
Устройство (прототип), реализующее способ (прототип), приведено на фиг.2, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блок 2 - вычислитель БПФ 1,

блок 3 - формирователь аналитического сигнала 1 (устройство обнуления отрицательных частот),

блоки 4.1 - 4.M - комплексные перемножители,

блоки 5.1 - 5.М - масштабирующие устройства с коэффициентами сжатия α _m=a^m,

блок 6 - устройство комплексного сопряжения,

блок 7 - формирователь аналитического сигнала 2 (устройство обнуления отрицательных частот),

блок 8 - вычислитель БПФ 2,

блок 9 - постоянное запоминающее устройство,

блоки 10.1 - 10.М - вычислители обратного БПФ,

блок 11 - устройство управления.

Принцип действия устройства заключается в следующем. Анализируемый сигнал s(t) поступает на АЦП (блок 1), с выхода которого дискретная выборка s(n) длиной N отсчетов поступает на вход вычислителя БПФ (блок 2). С выхода блока 2 комплексный спектр сигнала поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) 1 (блок 3). С выхода блока 3 спектр аналитического сигнала одновременно поступает на первые входы М комплексных перемножителей (блоки 4.1 - 4.M).

Из ПЗУ (блок 9) дискретная выборка "материнского" вейвлета ψ (n) поступает на вход вычислителя БПФ 2 (блок 8). С выхода блока 8 комплексный спектр вейвлета поступает на вход формирователя аналитического сигнала 2 (устройства обнуления отрицательных частот) (блок 7). С выхода блока 7 аналитический спектр вейвлета поступает на устройство комплексного сопряжения (блок 6).

С выхода блока 6 сопряженный спектр вейвлета одновременно поступает на входы М масштабирующих устройств (блоки 5.1 - 5.М) с коэффициентами сжатия α _m=a^m. Промасштабированные версии спектров вейвлет-функции Ψ _m(n) поступают на вторые входы М комплексных перемножителей (блоки 4.1 - 4.М), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 10.1 - 10.М).

С выходов М вычислителей обратного БПФ (блоки 10.1 - 10.М) снимаются результаты вейвлет-преобразования сигнала в виде массива значений вейвлет-коэффициентов размером М масштабов на N сдвигов Wψ {s}(m, n)=Wψ {s}(log_a α _m, τ _n).

Устройство управления (блок 11) осуществляет синхронизацию работы блоков АЦП (блок 1), вычислителей БПФ 1, 2, перемножителей (блоки 4.1 - 4.M), вычислителей обратного БПФ (блоки 10.1 - 10.M).

Для реализации данного способа вычисления избыточного дискретного вейвлет-преобразования с произвольным дискретным шагом масштаба в спектральной области, требуется:

- М операций масштабирования (сжатия) спектра исходного вейвлета (и, соответственно, столько же интерполяционных процедур),

- 2 операции прямого БПФ и М операций обратного БПФ, соответственно, примерно операций комплексного умножения,

с учетом того, что одна операция БПФ для сигнала длиной N отсчетов требует комплексных умножений [8 (с.647)].

Таким образом, существующие методы вычисления ВП можно разделить на два класса, обладающих следующими достоинствами и недостатками:

1) Методы вычисления дискретного вейвлет-преобразования на основе дискретизации вида (4) с грубым шагом дискретизации α _m=2^m, обладающие хорошим быстродействием, но не позволяющие анализировать сигнал с произвольной точностью измерения масштабов.

2) Методы вычисления ("непрерывного") избыточного дискретного вейвлет-преобразования с произвольно мелким шагом дискретизации масштабных коэффициентов α _m=a^m, 1<а<2, позволяющие анализировать сигнал с произвольной точностью измерения масштабов и временных сдвигов, но крайне не эффективные с точки зрения быстродействия и требуемых вычислительных и аппаратурных затрат (прототип).

Ниже предлагается новый способ и реализующие его устройства вычисления избыточного дискретного ВП сигналов с произвольно мелким дискретным логарифмическим шагом для масштабного коэффициента, причем значительно более эффективные с точки зрения быстродействия и вычислительных и аппаратурных затрат, чем прототип.

Теоретические основы предлагаемого способа

Как уже говорилось выше, оператор непрерывного вейвлет-преобразования (ВП) сигнала может быть определен в частотной области:

где Ψ (f) - образ Фурье выбранного вейвдета ψ (t),

S(f) - образ Фурье анализируемого сигнала s(t).

Путем введения новой спектральной функции оператор ВП (5) можно переписать в другом виде:

Масштабированный спектр вейвлета Ψ ₁(α f) преобразуем следующим образом для перевода мультипликативной операции умножения аргументов α и f в аддитивную операцию сложения:

где Ψ ₂(x)=Ψ ₁(a^x).

Т.о. оператор (6) можно записать в виде:

Выражение (8) является основой для варианта 1 предлагаемого способа быстрого вычисления избыточного дискретного ВП с произвольным шагом дискретизации для масштабных коэффициентов.

Заметим, что выбор значения основания логарифма а для предлагаемого способа означает и выбор основания для логарифмического шага дискретизации масштабных коэффициентов α _m=a^m.

Далее, введя новую переменную z=log_aαдля масштабирующего коэффициента, выражение (7) можно переписать:

Ψ ₁(α f)=Ψ ₂(log_aα+log_af)=Ψ ₂(z+log_af)

После этого оператор (8) можно преобразовать следующим образом. Формально записав два оператора - прямого и обратного преобразования Фурье, (соответственно по аргументам z и u), применим к только одно прямое преобразование Фурье по z:

где ψ ₂(u)=F_z{Ψ ₂(z)}.

В соответствии со свойством преобразования Фурье сдвиги log_af по аргументу z функции Ψ ₂(z) при этом перейдут в показатель экспоненты exp(-j2π ulog_af).

Оператор (9) является основой для варианта 2 предлагаемого способа вычисления ВП.

Сущность предлагаемого способа

Вариант 1. Первый вариант предлагаемого способа быстрого вычисления вейвлет-преобразования сигнала с произвольным шагом дискретизации по масштабному коэффициенту, основан на операторе (8) и включает в себя следующие операции:

1. Вычисление спектра Фурье S(f) исходного сигнала s(t) и обнуление отрицательных частот (преобразование его в спектр аналитического сигнала): S_A(f)=S(f) при f>0 и S_A(f)=0 при f≤ 0.

2. Деление на корень из частоты

3. Выбор исходного вейвлета ψ (t), вычисление его спектра Фурье Ψ (f), комплексное сопряжение и обнуление отрицательных частот (приведение к аналитическому виду): при f>0 и при f≤ 0.

4. Умножение на корень из частоты:

5. Логарифмическое масштабирование (преобразование) аргумента: f→ log_af. При этом спектральная функция вейвлета преобразуется:

6. Формирование сдвигов log_af функции по аргументу z:

7. Перемножение спектра сигнала и двумерной функции

8. Обратное преобразование Фурье по f:

Заметим, что операции 3-6 производятся только с вейвлетом, а не с исследуемым сигналом, и т.о. могут быть проведены заранее, а результаты расчетов храниться в ПЗУ (вариант 2 устройства, реализующего вариант 1 предлагаемого способа вычислений).

Вариант 2. Второй вариант предлагаемого способа быстрого вычисления вейвлет-преобразования сигнала с произвольным шагом дискретизации по масштабному коэффициенту основан на операторе (9) и включает в себя следующие операции:

Операции 1-5 идентичны варианту 1, и далее:

6. Прямое преобразование Фурье:

7. Формирование (или извлечение из памяти заранее рассчитанного) двумерного массива экспонент: Е(u, f)=ехр(-j2π ulog_af).

8. Перемножение функции и экспонент E(u,f).

9. Перемножение спектра сигнала и результата произведения

10. Обратное двумерное преобразование Фурье по u и f:

Заметим, что операции 3-7 производятся только с вейвлетом, а не с исследуемым сигналом, и т.о. могут быть проведены заранее, а результаты расчетов храниться в ПЗУ (вариант 2 устройства, реализующего вариант 2 предлагаемого способа),

Устройства, реализующие предлагаемый способ

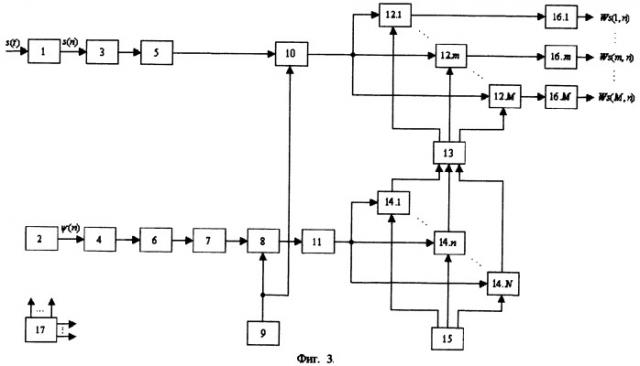
Вариант 1 устройства, реализующего вариант 1 предлагаемого способа вычисления ВП сигнала на основе оператора (8), приведен на фиг.3, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блок 2 - ПЗУ 1,

блок 3 - вычислитель БПФ 1,

блок 4 - вычислитель БПФ 2,

блок 5 - формирователь аналитического сигнала (устройство обнуления отрицательных частот) 1,

блок 6 - формирователь аналитического сигнала (устройство обнуления отрицательных частот) 2,

блок 7 - устройство комплексного сопряжения,

блок 8 - перемножитель,

блок 9 - ПЗУ 2,

блок 10 - делитель,

блок 11 - устройство логарифмического масштабирования (преобразования аргумента сигнальной функции вида f→ log_af),

блоки 12.1 - 12.М - комплексные перемножители,

блок 13 - оперативное запоминающее устройство (ОЗУ),

блоки 14.1 - 14.N - устройства сдвига,

блок 15 - ПЗУ 3,

блоки 16.1 - 16.М - вычислители обратного БПФ,

блок 17 - управляющее устройство.

Т.о. первый вариант устройства, реализующего первый вариант предлагаемого способа, содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, а выход которого соединен с входом первого вычислителя быстрого преобразования Фурье (блок 3), выход которого соединен с входом первого блока обнуления отрицательных частот (блок 5), выход которого соединен с первым входом делителя (блок 10), выход которого соединен с первыми входами перемножителей (блоки 12.1 - 12.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 16.1 - 16.M), выходы которых являются выходом устройства; первое постоянное запоминающее устройство (блок 2), выход которого соединен с входом второго вычислителя быстрого преобразования Фурье (блок 4), выход которого соединен со входом второго блока обнуления отрицательных частот (блок 6), выход которого соединен со входом блока комплексного сопряжения (блок 7), выход которого соединен с первым входом перемножителя (блок 8), выход которого соединен с входом устройства логарифмического масштабирования (блок 11), выход которого соединен с первыми входами N устройств сдвига (блоки 14.1 - 14.N), выходы которых соединены с N входами оперативного запоминающего устройства (блок 13), М выходов которого соединены со вторыми входами М перемножителей (блоки 12.1 - 12.M); управляющее устройство (блок 17), выходы которого соединены с управляющими входами аналого-цифрового преобразователя (блок 1), вычислителей быстрого преобразования Фурье (блоки 3 и 4), перемножителей (блоки 8, 12.1 - 12.М), устройств сдвига (блоки 14.1 - 14.N), оперативного запоминающего устройства (блок 13), вычислителей обратного быстрого преобразования Фурье (блоки 16.1 - 16.M).

Принцип действия устройства заключается в следующем. Анализируемый сигнал s(t) поступает на АЦП (блок 1), с выхода которого дискретная выборка s(n) длиной N отсчетов поступает на вход вычислителя БПФ 1 (блок 3). С выхода блока 3 комплексный спектр S(n) сигнала поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) 1 (блок 5). С выхода блока 5 спектр аналитического сигнала S_A(n) поступает на первый вход делителя (блок 10), на второй вход которого из ПЗУ 2 (блок 9) поступает массив значений (При этом первый (нулевой) отсчет S_A(0)=0 на ноль не делится и остается равным нулю).

С выхода блока 10 результат деления поступает одновременно на первые входы перемножителей (12.1 - 12.M).

Из ПЗУ 1 (блок 2) дискретная выборка "материнского" вейвлета Ψ (n) поступает на вход вычислителя БПФ 2 (блок 4). С выхода блока 4 комплексный спектр вейвлета Ψ _A(n) поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) 2 (блок 6). С выхода блока 6 спектр вейвлета Ψ _A(n) поступает на вход устройства комплексного сопряжения (блок 7). С выхода блока 7 сопряженный спектр вейвлета поступает на первый вход перемножителя 1 (блок 8), на второй вход которого из ПЗУ 2 (блок 9) поступает массив значений

С выхода перемножителя 1 (блок 8) результат перемножения длиной N отсчетов поступает на вход устройства логарифмического масштабирования (блок 11). С выхода блока 11 результат логарифмического масштабирования Ψ ₂(m) длиной М отсчетов (количество отсчетов М и основание логарифма масштабирования а выбираются исходя из заданного значения шага дискретизации масштаба и максимального значения коэффициента сжатия) одновременно поступает на первые входы устройств сдвига (блоки 14.1 - 14.N).

С выходов ПЗУ 3 (блок 15) на вторые входы устройств сдвига (блоки 14.1 - 14.N) одновременно поступают значения N сдвигов (здесь квадратные скобки означают операцию выбора целой части значения логарифма).

С выходов устройств сдвига (блоки 14.1 - 14.N) N сдвинутых версий Ψ ₂(m+ν _n), длиной по М отсчетов, одновременно поступают на входы ОЗУ (блок 13), в котором в итоге формируется двумерный массив значений Ψ ₃(m,n)=Ψ ₂(m+ν _n) из N строк и М столбцов. С выходов ОЗУ (блок 13) одновременно считывается М одномерных массивов (столбцов) Ψ ₃(n,m₀) длиной по N отсчетов и поступает на вторые входы перемножителей (блоки 12.1 - 12.M), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 16.1 - 16.М).

С выходов М вычислителей обратного БПФ (блоки 16.1 - 16.М) снимаются результаты вейвлет-преобразования входного сигнала s(t) в виде двумерного массива значений вейвлет-коэффициентов размером М масштабов на N сдвигов Wψ {s}(m,n)=Wψ {s}(log_aα _m,τ _n).

Устройство управления (блок 17) осуществляет синхронизацию работы блоков АЦП (блок 1), вычислителей БПФ (блоки 3 и 4), умножителей (блоки 8, 12.1 - 12.M), устройств сдвига (блоки 14.1 - 14.N), ОЗУ (блок 13), вычислителей обратного БПФ (блоки 16.1 - 16.M).

Для реализации данного способа вычисления дискретного избыточного ВП с произвольным логарифмическим дискретным шагом масштаба требуется:

- всего 1 операция логарифмического масштабирования спектральной функции исходного вейвлета (и, соответственно, одна интерполяционная процедура),

- 2 операции прямого БПФ и М операций обратного БПФ (соответственно, операций комплексного умножения).

Данное устройство, реализующее предлагаемый способ, позволяет выбирать для анализа входного сигнала различные типы вейвлет-функции, хранящиеся в ПЗУ 1 (блок 2).

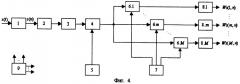
Вариант 2 устройства, реализующего вариант 1 предлагаемого способа вычисления ВП сигнала на основе оператора (8), приведен на фиг.4, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блок 2 - вычислитель БПФ,

блок 3 - формирователь аналитического сигнала (устройство обнуления отрицательных частот),

блок 4 - делитель,

блок 5 - ПЗУ 1,

блок 6.1 - 6.М - комплексные перемножители,

блок 7 - ПЗУ 2,

блоки 8.1 - 8.M - вычислители обратного БПФ,

блок 9 - управляющее устройство.

Т.о. второй вариант устройства, реализующего первый вариант предлагаемого способа, содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, а выход которого соединен с входом вычислителя быстрого преобразования Фурье (блок 2), выход которого соединен с входом блока обнуления отрицательных частот (блок 3), выход которого соединен с первым входом делителя (блок 4), выход которого соединен с первыми входами перемножителей (блоки 6.1 - 6.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 8.1 - 8.M), выходы которых являются выходом устройства; первое постоянное запоминающее устройство (блок 5), выход которого соединен со вторым входом делителя (блок 4); второе постоянное запоминающее устройство (блок 7), М выходов которого соединены со вторыми входами М перемножителей (блоки 6.1 - 6.M); управляющее устройство (блок 9), выходы которого подсоединены к управляющим входам аналого-цифрового преобразователя (блок 1), вычислителя быстрого преобразования Фурье (блок 2), перемножителей (блоки 4, 6.1 - 6.М), вычислителей обратного быстрого преобразования Фурье (блоки 8.1 - 8.M).

Принцип действия устройства заключается в следующем. Анализируемый сигнал s(t) поступает на АЦП (блок 1), с выхода которого дискретная выборка s(n) длиной N отсчетов поступает на вход вычислителя БПФ (блок 2). С выхода блока 2 комплексный спектр сигнала S(n) поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) (блок 3). С выхода блока 3 спектр аналитического сигнала S_A(n) поступает на первый вход делителя (блок 4), на второй вход которого из ПЗУ 1 (блок 5) поступает массив значений (При этом первый (нулевой) отсчет S_A(0)=0 на ноль не делится и остается равным нулю).

С выхода блока 4 результат деления поступает одновременно на первые входы перемножителей (6.1 - 6.М).

С выходов ПЗУ (блок 7) считывается М одномерных массивов Ψ ₃(n,m₀) длиной по N отсчетов и поступает на вторые входы перемножителей (блоки 6.1 - 6.M), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 8.1 - 8.M).

С выходов М вычислителей обратного БПФ (блоки 8.1 - 8.M) снимаются результаты вейвлет-преобразования входного сигнала s(t) в виде двумерного массива значений вейвлет-коэффициентов размером М масштабов на N сдвигов Wψ {s}(m,n)=Wψ {s}(log_aα _m,τ _n).

Устройство управления (блок 9) осуществляет синхронизацию работы блоков АЦП (блок 1), вычислителя БПФ (блоки 2), делителя (блок 4), умножителей (блоки 6.1 - 6.M), вычислителей обратного БПФ (блоки 8.1 - 8.M).

Для реализации первого варианта предлагаемого способа вычисления дискретного избыточного ВП с произвольным дискретным шагом масштаба устройством (вариант 2) требуется:

- 1 операция прямого БПФ и М операций обратного БПФ (соответственно, операций комплексного умножения).

Вариант 1 устройства, реализующего вариант 2 предлагаемого способа вычисления ВП сигнала на основе оператора (9), приведен на фиг.5, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блок 2 - ПЗУ 1,

блок 3 - вычислитель БПФ 1,

блок 4 - вычислитель БПФ 2,

блок 5 - формирователь аналитического сигнала (устройство обнуления отрицательных частот) 1,

блок 6 - формирователь аналитического сигнала (устройство обнуления отрицательных частот) 2,

блок 7 - устройство комплексного сопряжения,

блок 8 - перемножитель,

блок 9 - ПЗУ 2,

блок 10 - делитель,

блок 11 - устройство логарифмического масштабирования (преобразования аргумента сигнальной функции вида f→ log_af),

блок 12 - вычислитель БПФ 3,

блок 13 - ПЗУ 3

блок 14 - матричный перемножитель 1,

блок 15 - устройство возведения в степень,

блок 16 - ПЗУ 4,

блок 17 - матричный перемножитель 2,

блок 18 - вычислитель двумерного обратного БПФ,

блок 19 - управляющее устройство.

Т.о. первый вариант устройства, реализующего второй вариант предлагаемого способа, содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, а выход которого соединен с входом первого вычислителя быстрого преобразования Фурье (блок 3), выход которого соединен с входом первого блока обнуления отрицательных частот (блок 5), выход которого соединен с первым входом делителя (блок 10), выход которого соединен с первым входом второго матричного перемножителя (блок 17), выход которого соединен с входом вычислителя двумерного обратного быстрого преобразования Фурье (блок 18), выход которого является выходом устройства; первое постоянное запоминающее устройство (блок 2), выход которого соединен с входом второго вычислителя быстрого преобразования Фурье (блок 4), выход которого соединен со входом второго блока обнуления отрицательных частот (блок 6), выход которого соединен со входом блока комплексного сопряжения (блок 7), выход которого соединен с первым входом умножителя (блок 8), выход которого соединен с входом устройства логарифмического масштабирования (блок 11), выход которого соединен с входом третьего вычислителя быстрого преобразования Фурье (блок 12), выход которого соединен с первым входом первого матричного умножителя (блок 14), выход которого соединен со вторым входом второго матричного умножителя (блок 17); второе постоянное запоминающее устройство (блок 9), выход которого соединен со вторым входом делителя (блок 10) и со вторым входом умножителя (блок 8); третье постоянное запоминающее устройство (блок 13), выход которого соединен с первым входом устройства возведения в степень (блок 15); четвертое постоянное запоминающее устройство (блок 16), выход которого соединен со вторым входом устройства возведения в степень (блок 15), выход которого соединен со вторым входом первого матричного умножителя (блок 14); управляющее устройство (блок 19), выходы которого подсоединены к управляющим входам аналого-цифрового преобразователя (блок 1), перемножителей (блоки 8, 14, 17), вычислителей быстрого преобразования Фурье (блоки 3, 4, 12), делителя (блок 10), вычислителя двумерного обратного быстрого преобразования Фурье (блок 18).

Принцип действия устройства заключается в следующем. Анализируемый сигнал s(t) поступает на АЦП (блок 1), с выхода которого дискретная выборка s(n) длиной N отсчетов поступает на вход вычислителя БПФ 1 (блок 3). С выхода блока 3 комплексный спектр сигнала S(n) поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) 1 (блок 5). С выхода блока 5 спектр аналитического сигнала S_A(n) поступает на первый вход делителя (блок 10), на второй вход которого из ПЗУ 2 (блок 9) поступает массив значений (При этом первый (нулевой) отсчет S_A(0)=0 на ноль не делится и остается равным нулю).

С выхода блока 10 результат деления поступает на первый вход матричного перемножителя 2 (блок 17).

Из ПЗУ 1 (блок 2) дискретная выборка "материнского" вейвлета ψ (n) поступает на вход вычислителя БПФ 2 (блок 4). С выхода блока 4 комплексный спектр вейвлета Ψ (n) поступает на вход формирователя аналитического сигнала (устройства обнуления отрицательных частот) 2 (блок 6). С выхода блока 6 спектр вейвлета Ψ _A(n) поступает на вход устройства комплексного сопряжения (блок 7). С выхода блока 7 сопряженный спектр вейвлета поступает на первый вход перемножителя 1 (блок 8), на второй вход которого из ПЗУ 2 (блок 9) поступает массив значений

С выхода перемножителя 1 (блок 8) результат перемножения длиной N отсчетов, поступает на вход устройства логарифмического масштабирования (блок 11). С выхода блока 11 результат логарифмического масштабирования Ψ ₂(m) длиной М отсчетов (количество отсчетов М и основание логарифма масштабирования a выбираются исходя из заданного значения шага дискретизации масштаба и максимального значения коэффициента сжатия) поступает на вычислитель БПФ 3 (блок 12). С выхода блока 12 результат преобразования ψ ₂(m) поступает на первый вход матричного перемножителя 2 (блок 14).

Из ПЗУ 4 (блок 16) на первый вход устройства возведения в степень (