Способ сжатия и восстановления сообщений

Способ сжатия и восстановления сообщений

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи, а именно, к методам цифровых вычислений и обработки данных с сокращением избыточности передаваемой информации. Предлагаемый способ может быть использован для передачи неподвижных видеоизображений по цифровым каналам связи и относится к классу способов кодирования-восстановления на основе преобразования.

Известны способы кодирования видеоизображений на основе импульсно-кодовой модуляции, дифференциальной импульсно-кодовой модуляции, статистического кодирования и кодирования с предсказанием, см., например, книгу: У.Претт Цифровая обработка изображений Часть 2. - М.: Мир, 1982, с.641-688. Данные способы подразумевают кодирование изображений с поэлементной обработкой, когда непрерывный видеосигнал преобразуется в последовательность квантованных отсчетов и затем представляется кодовыми словами в виде нулей и единиц.

Известны также способы кодирования на основе преобразования, см., например, книгу: Н.Ахмед. К.Р.Рао Ортогональные преобразования при обработке цифровых сигналов. - М.: Радио и связь, 1980, с.192-201, включающие выполнение трех операций: сначала изображение подвергается двумерному ортогональному преобразованию, полученные в результате коэффициенты преобразования квантуются и в дальнейшем кодируются для передачи по каналу связи.

Недостатком перечисленных выше способов - аналогов является относительно низкая скорость передачи сообщений при заданном качестве их восстановления.

Наиболее близким по своей технической сущности к заявленному способу является способ сжатия и восстановления речевых сообщений, описанный в патенте РФ №2152646 А, МПК⁷ G 10 L 3/02 от 2000 г.

Известный способ-прототип заключается в том, что предварительно идентично на передающей стороне и на приемной стороне генерируют случайную квадратную матрицу квантованных дискретных отсчетов размером mxm элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала. Непрерывный речевой сигнал дискретизируют и квантуют дискретные отсчеты. Затем формируют матрицу нормированных значений речевого сигнала размером NxN элементов так, что каждому ее элементу А_j,i, где j=1,2,...,N; i=1,2,...,N, присваивают квантованное значение дискретного отсчета речевого сигнала, k-й номер которого определяют в соответствии с выражением: k=j+N·(i-1). Матрицу квантованных отсчетов речевого сигнала размером NxN элементов преобразуют к цифровому виду путем формирования множества нулевых и единичных элементов в виде прямоугольных матриц размером Nxm и mxN элементов. Для этого генерируют случайные прямоугольные матрицы из единичных и нулевых элементов размером Nxm и mxN элементов. Затем преобразуют случайные прямоугольные матрицы размером Nxm и mxN элементов путем деления элементов каждой строки случайной прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки и деления элементов каждого столбца случайной прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца. После этого вычисляют результирующую матрицу размером NxN элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером Nxm элементов, случайной квадратной матрицы квантованных дискретных отсчетов размером mxm элементов и полученной после преобразования прямоугольной матрицы размером mxN элементов. Вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером NxN элементов и элементами матрицы нормированных значений речевого сигнала размером NxN элементов. Затем последовательно инвертируют каждый элемент случайных прямоугольных матриц размером Nxm и mxN элементов, преобразуют их и последовательно перемножают полученную после преобразования прямоугольную матрицу размером Nxm элементов, случайную квадратную матрицу квантованных дискретных отсчетов размером mxm элементов и полученную после преобразования прямоугольную матрицу размером mxN элементов. Вычисляют сумму квадратов разностей между элементами полученной в результате перемножения результирующей матрицы размером NxN и элементами матрицы нормированных значений речевого сигнала размером NxN элементов. Вычитают эту сумму от аналогичной суммы, полученной на предыдущем шаге, и, в случае положительной разности, сохраняют инвертированное значение элемента, а в противном случае - выполняют его повторную инверсию. После этого передают множество нулевых и единичных элементов прямоугольных матриц размером Nxm и mxN элементов по каналу связи. Принимают множество нулевых и единичных элементов прямоугольных матриц размером Nxm и mxN элементов из канала связи и преобразуют путем деления элементов каждой строки прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки и деления элементов каждого столбца прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца. Затем формируют матрицу восстановленных нормированных значений сигнала размером NxN элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером Nxm элементов, случайной квадратной матрицы квантованных дискретных отсчетов размером mxm элементов и полученной после преобразования прямоугольной матрицы размером mxN элементов. На последнем этапе матрицу восстановленных нормированных значений речевого сигнала размером NxN элементов преобразуют в непрерывный речевой сигнал.

Способ-прототип позволяет, не ухудшая качества восстановления сообщений, повысить скорость передачи информации до величины, при которой возможно ведение телефонных переговоров по низкоскоростным цифровым каналам связи.

Недостатком этого способа-прототипа все же является относительно низкая скорость передачи информации. Поскольку в способе-прототипе кодируют непосредственно квантованные дискретные отсчеты сообщения, то для восстановления сообщения с заданным качеством необходимо кодировать большой массив данных, что ограничивает возможность применения данного способа для передачи неподвижных видеоизображений.

Целью изобретения является разработка способа сжатия и восстановления сообщений, обеспечивающего увеличение скорости передачи информации с сохранением заданного качества восстановления сообщений.

Поставленная цель достигается тем, что в известном способе сжатия и восстановления сообщений предварительно на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу размером mxm элементов, представляют информационный цифровой сигнал в виде матрицы нормированных значений, генерируют случайные прямоугольные матрицы размером Nxm и mxN элементов, преобразуют их путем деления элементов каждой строки случайной прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки и деления элементов каждого столбца случайной прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца, вычисляют результирующую матрицу размером NxN элементов, путем последовательного умножения преобразованной случайной прямоугольной матрицы размером Nxm на случайную квадратную матрицу размера mxm и на преобразованную случайную прямоугольную матрицу размером mxN элементов, затем вычисляют среднеквадратическую ошибку между элементами результирующей матрицы размером NxN элементов и элементами матрицы нормированных значений размером NxN элементов, после чего последовательно инвертируют каждый элемент случайных прямоугольных матриц размером Nxm и mxN элементов, и после инверсии каждого элемента в случайной прямоугольной матрице преобразуют ее путем деления элементов каждой строки случайной прямоугольной матрицы с инвертированным элементом размером Nxm элементов на сумму единиц соответствующей строки и деления элементов каждого столбца случайной прямоугольной матрицы с инвертированным элементом размером mxN элементов на сумму единиц соответствующего столбца, повторно вычисляют результирующую матрицу размером NxN элементов, путем последовательного умножения преобразованной случайной прямоугольной матрицей с инвертированным элементом размером Nxm на случайную квадратную матрицу размера mxm и на преобразованную случайную прямоугольную матрицу с инвертированным элементом размером mxN, после чего вычисляют среднеквадратическую ошибку между элементами повторно вычисленной результирующей матрицы размером NxN элементов с элементами матрицы нормированных значений размером NxN элементов, передают по каналу связи случайную прямоугольную матрицу размером Nxm, принимают из канала связи эту матрицу и на приемном конце преобразуют принятые случайные прямоугольные матрицы размера Nxm и mxN путем деления элементов строки каждой случайной прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки и деления элементов каждого столбца случайной прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца, вычисляют результирующую матрицу размера NxN элементов, путем последовательного умножения преобразованной случайной прямоугольной матрицы размера Nxm на случайную квадратную матрицу размера mxm и на преобразованную случайную прямоугольную матрицу размера mxN, формируют цифровой информационный сигнал, на приемной и передающей сторонах дополнительно генерируют по k случайных ключевых матриц размером Nxm и mxN элементов. Каждый элемент случайной квадратной матрицы размером mxm элементов принадлежит диапазону -500-+500, в качестве цифрового информационного сигнала принимают k-матриц квантованных отсчетов неподвижного полутонового изображения размерами МxМ, где k>1. Генерируют на приемной и передающей сторонах идентичную нормировочную матрицу размера NxN элементов, элементы которой C(i,j) вычисляют по формуле где i=1, 2,...,N, j=1, 2,...,N. В качестве случайной прямоугольной матрицы размером mxN элементов принимают на передающей стороне транспонированную случайную прямоугольную матрицу размером Nxm элементов. Формируют k-матриц коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов путем последовательного перемножения матрицы дискретно-косинусного преобразования размером МxМ элементов на каждую матрицу квантованных отсчетов неподвижного полутонового видеоизображения размером МxМ элементов и на транспонированную матрицу дискретно-косинусного преобразования размером МxМ элементов. Далее формируют k-матриц коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов, по формуле A_g(i,j)=L_g(i,j), где i=1, 2,...,N, j=1, 2,...,N, g=1,2,...,k, L_g(i,j) - i,j-й элемент g-й матрицы коэффициентов двумерного дискретного косинусного преобразования размером МxМ элементов, A_g(i,j) - i,j-й элемент g-й матрицы коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов, причем выбирают N<M. Затем формируют k-матриц нормированных значений размером NxN элементов, путем умножения каждого коэффициента матрицы коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов A_g(i,j) на соответствующий ему элемент нормировочной матрицы размером NxN элементов. Каждую из ключевых матриц размерами Nxm и mxN элементов суммируют по модулю 2 соответственно с прямой и транспонированной случайной прямоугольной матрицей размерами Nxm и mxN элементов, а после вычисления среднеквадратической ошибки между соответствующими элементами каждой результирующей матрицы размером NxN элементов и матрицы нормированных значений размером NxN элементов, вычисляют их итоговую сумму. После инвертирования каждого элемента случайной прямоугольной матрицы размером Nxm полученную итоговую сумму сравнивают с предыдущей итоговой суммой. По каналу связи передают случайную прямоугольную матрицу размером Nxm элементов, а на приемной стороне после перемножения k-случайных матриц размерами Nxm на случайную матрицу размером mxm и на k-случайных матриц размерами mxN, преобразуют результирующие матрицы размерами NxN элементов путем поэлементного деления их элементов на соответствующие элементы нормировочной матрицы размером NxN элементов. Полученные k-матрицы восстановленных коэффициентов размерами NxN элементов дополняют нулями до размеров МxМ элементов. Восстанавливают k-матриц неподвижных полутоновых изображений, путем последовательного перемножения транспонированной матрицы дискретно-косинусного преобразования размером МxМ элементов на k-матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов и на матрицу дискретно-косинусного преобразования размером МxМ элементов. Для формирования k-матриц квантованных отсчетов неподвижного полутонового видеоизображения размерами МxМ элементов каждому ее элементу S_g(x,y), где х=1,2,...,М; y=1,2,...,М, g=1,2,...,k, присваивают квантованное значение соответствующего пиксела k-неподвижных полутоновых видеоизображений, размером NxN. Для представления k-матриц квантованных отсчетов неподвижного полутонового видеоизображения размером МxМ элементов в виде k-неподвижных полутоновых видеоизображений каждому пикселу k-неподвижных полутоновых видеоизображений присваивают значение соответствующего элемента k-магриц восстановленных квантованных отсчетов неподвижных полутоновых видеоизображений размером МxМ элементов.

Благодаря новой совокупности существенных признаков за счет выполнения дискретного косинусного преобразования над k-матрицами квантованных отсчетов неподвижного полутонового видеоизображения обеспечивается переход к представлению видеоизображения в виде k-матриц спектральных коэффициентов. Для уменьшения цифрового представления видеоизображения кодируют и передают не все спектральные коэффициенты, а только N² спектральных коэффициентов из области спектра с максимальной энергией.

Все это позволяет, не ухудшая качества восстановления сообщений, повысить скорость передачи информации до величины, при которой возможна передача неподвижных полутоновых видеоизображений по низкоскоростным цифровым каналам связи (32 кбит/с).

Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности “новизна”. Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности “изобретательский уровень”.

Заявленный способ поясняется чертежами:

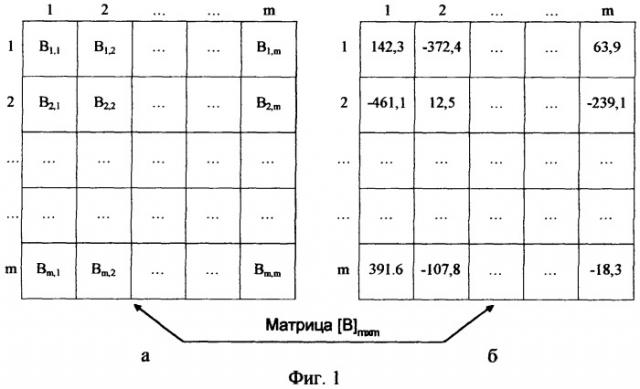
- Фиг.1а - формирование случайной квадратной матрицы размером mxm элементов.

- Фиг.1б - вариант случайной квадратной матрицы размером mxm элементов.

- Фиг.2 - формирование k-матриц коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов.

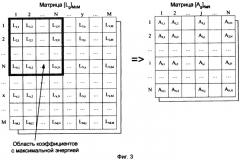
- Фиг.3 - формирование k-матриц коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов.

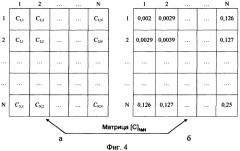
- Фиг.4а, 4б - формирование нормировочной матрицы размером NxN элементов.

- Фиг.5 - формирование k-матриц нормированных значений размером NxN элементов.

- Фиг.6а - формирование k-случайных ключевых матриц размером Nxm элементов.

- Фиг.6б - вариант k-случайных ключевых матриц размером Nxm элементов.

- Фиг.6в - формирование k-случайных ключевых матриц размером mxN элементов.

- Фиг.6г - вариант k-случайных ключевых матриц размером mxN элементов.

- Фиг 7а - формирование k-случайных прямоугольных матриц размером Nxm элементов.

- Фиг.7б - вариант k-случайных прямоугольных матриц размером Nxm элементов.

- Фиг.7в - формирование k-случайных прямоугольных матриц размером Nxm элементов.

- Фиг.7г - формирование k-случайных прямоугольных матриц размером mxN элементов.

- Фиг.7д - преобразование k-случайных прямоугольных матриц размером Nxm элементов.

- Фиг.7е - преобразование k-случайных прямоугольных матриц размером mxN элементов.

- Фиг.8 - формирование k-результирующих матриц размером NxN элементов.

- Фиг.9а - вариант инверсии элемента случайной прямоугольной матрицы размером Nxm элементов.

- Фиг.10 - передача случайной прямоугольной матрицы размером Nxm элементов по цифровому каналу связи.

- Фиг.11а - вариант матрицы коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов.

- Фиг.11б - график абсолютных значений первой строки матрицы коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов.

- Фиг.12 - формирование k-матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов.

- Фиг.13 - формирование k-матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов.

- Фиг.14 - формирование k-матриц восстановленных квантованных отсчетов неподвижного полутонового видеоизображения.

Возможность реализации заявленного способа сжатия и восстановления сообщений объясняется следующим. При необходимости передачи по каналу связи сообщения, объем которого превышает возможности канала связи или для передачи которого требуется недопустимо большой временной интервал, используют различные приемы сокращения объема передаваемого сообщения.

Например (см. книгу: У.Претт. Цифровая обработка изображений. Часть 1. - М.: Мир, 1982, с.96-118), кодируемое сообщение представляют в виде произведения матрицы опорных векторов на матрицу коэффициентов разложения. Для этой цели используют один из известных приемов: дискретное косинусное преобразование, быстрое преобразование Фурье, преобразование Карунена-Лоэва, Вейвлет-преобразование и другие.

Такой прием обуславливает некоторое снижение объема информации, необходимого для передачи по каналу связи, и одновременное достижение требуемого качества.

На приемном конце принятое сообщение восстанавливают.

Таким образом, при некотором ухудшении качества передаваемой информации обеспечивают снижение объема информации, необходимого для передачи. В то же время объем передаваемой информации о матрице опорных векторов и матрице коэффициентов разложения все еще велик, что не соответствует требованиям к современным каналам связи при сохранении требуемого качества. В предлагаемом способе решается задача снижения объема передаваемой информации при одновременном сохранении требуемого качества.

Предлагаемый способ предполагает проведение следующих действий.

Формирование на передающей и приемной сторонах случайной квадратной матрицы размером mxm элементов (в дальнейшем обозначим ее как [B]_mxm), каждый элемент которой принадлежит диапазону -500-+500 (см. фиг.1а, 1б). Размер m матрицы [В]_mxm выбирают опытным путем исходя из размера передаваемого сообщения - M. Экспериментальные исследования показывают, что для качественной аппроксимации передаваемого сообщения размер m составляет 1/5-1/4 размера передаваемого сообщения. Операция формирования матрицы [B]_mxm может быть выполнена с использованием датчика случайных чисел. Для выполнения требования идентичности матрицы [B]_mxm приемника аналогичной матрице передатчика элементы матрицы [B]_mxm могут быть сгенерированы на передающей стороне и переданы по цифровому каналу связи на приемную сторону, например, в составе синхропосылки.

В качестве k-сообщений, подлежащих сжатию и восстановлению, далее рассматриваются k-неподвижные полутоновые видеоизображения, из которых формируют k-матриц квантованных отсчетов неподвижного полутонового видеоизображения размером МxМ элементов, для каждого видеоизображения, присвоив каждому ее элементу S_g(х,y), где х=1,2,...,М; y=1,2,...,М, квантованное значение соответствующего пиксела неподвижного полутонового видеоизображения своей картинки, g=1,...,k номер неподвижного полутонового видеоизображения (см. рис.1 приложения 1).

С целью уменьшения объема информации, передаваемой по каналу связи, используют дискретное косинусное преобразование, описанное, например, в кн.: Н.Ахмед, К.Р.Рао Ортогональные преобразования при обработке цифровых сигналов. - М.: Связь, 1980, с.156-159.

Матрицу коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов формируют на основании выражения [L_g(x,y)]_MxM=[Г(x,y)]_MxMx[S_g(x,y)]_MxMx[Г(x,y)]_MxM, где [L_g(x,y)]_MxM - матрица коэффициентов двумерного дискретно-косинусного преобразования g-го неподвижного полутонового видеоизображения размером МxМ элементов, [S_g(x,y)]_MxM - матрица квантованных отсчетов g-го неподвижного полутонового видеоизображения размером МxМ элементов, [Г(х,y)]_MxM - матрица прямого дискретного косинусного преобразования, [Г(х,y)]_MxM^- матрица обратного дискретного косинусного преобразования (см. фиг.2).

Наиболее информативными, с точки зрения восстановления передаваемого видеоизображения, являются коэффициенты двумерного дискретно-косинусного преобразования с максимальной энергией, располагающиеся в левом верхнем квадранте матрицы коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов (см. фиг.11а). Их выделяют, формируя матрицу коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов (в дальнейшем обозначим ее как ), на основании выражения A_g(i,j)=L_g(i,j), где i=1, 2,...,N, j=1, 2,...,N, L_g(i,j) - i,j-й элемент матрицы коэффициентов двумерного дискретного косинусного преобразования g-го неподвижного полутонового видеоизображения размером МxМ элементов, A_g(i,j) - i,j-й элемент матрицы коэффициентов двумерного дискретно-косинусного преобразования g-го неподвижного полутонового видеоизображения размером NxN элементов, причем выбирают N≤M (см. фиг.3).

Величина коэффициентов двумерного дискретно-косинусного преобразования в большой степени зависит от их порядкового номера, о чем можно судить исходя из графика (см. фиг.11б), где по оси абсцисс отложены порядковые номера коэффициентов первой строки матрицы коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов, а по оси ординат - их абсолютные значения. Для того чтобы устранить зависимость величины элементов матицы коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов от их местоположения в матрице и в дальнейшем более точно их аппроксимировать, необходимо произвести операцию нормирования. Суть данной операции заключается в том, что на передающей и приемной сторонах идентично формируют нормировочную матрицу размером NxN элементов (в дальнейшем обозначим ее как [С]_NxN), элементы которой C(i,j) вычисляют по формуле (см. фиг.4), полученную опытным путем. При этом учтена особенность матрицы коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов, заключающаяся в расположении коэффициентов с максимальной энергией в левом верхнем квадранте и зависимости значений коэффициентов от их порядкового номера (i и j).

Затем формируют k-матриц нормированных значений двумерного дискретно-косинусного преобразования размером NxN элементов, путем умножения каждого элемента A_g(i,j) матрицы коэффициентов двумерного дискретно-косинусного преобразования g-го неподвижного полутонового видеоизображения размером NxN элементов на соответствующий ему элемент C(i,j) нормировочной матрицы размером NxN элементов (см. фиг.5). Аналогичным образом, используя нормировочную матрицу, нормируют коэффициенты дискретно-косинусного преобразования в стандарте сжатия JPEG.

Далее, аналогично способу-прототипу используют подход, основанный на представлении матрицы нормированных коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов [V(k)]_NxN в виде произведения трех матриц: преобразованной прямоугольной матрицы размером Nxm элементов (в дальнейшем обозначим ее как ), случайной квадратной матрицы размером mxm элементов [B]_mxm и преобразованной прямоугольной матрицы размером mxN элементов (в дальнейшем обозначим ее как ) (см. фиг.8). Тогда, при кодировании матрицы [V(k)]_NxN на передающем конце необходимо найти такие оптимальные матрицы и которые при перемножении с матрицей [B]_mxm образуют результирующую матрицу размером NxN элементов (в дальнейшем обозначим эту матрицу как ), наиболее близкую по заданному критерию к матрице [V(k)]_NxN.

Матрицы и формируют путем произведения случайной прямоугольной матрицы [E]_Nxm на k-тую случайную ключевую матрицу [Y_кл(k)]_Nxm и транспонированную случайную прямоугольную матрицу [Е]

T

Nxm

на k-тую случайную ключевую матрицу [X_кл(k)]_mxN соответственно, где матрицы [Y_кл(k)]_Nxm и [X_кл(k)]_mxN являются ключом k-го неподвижного полутонового видеоизображения размером mxN (см. фиг.7в, 7г).

Особенностью матриц и является то, что они могут быть легко приведены к цифровому виду. Это достигается тем, что на элементы этих матриц накладываются следующие ограничения:

- элементы матриц и принимают значения в диапазоне от нуля до единицы;

- ненулевые элементы каждой строки матрицы равны между собой и в сумме образуют единицу;

- ненулевые элементы каждого столбца матрицы равны между собой и в сумме образуют единицу.

При таких ограничениях, если элементы каждой строки матрицы умножить на количество ненулевых элементов в этой строке, то будет получена матрица [Y(k)]_Nxm, элементы которой определены только на множестве “1” и “0”. Аналогично, если элементы каждого столбца матрицы умножить на количество ненулевых элементов в столбце, то будет получена матрица элементы которой определены только на множестве “1” и “0”.

Процедура, реализующая поиск на передающей стороне оптимальных матриц и подробно описана в способе-прототипе (см. патент РФ №2152646 А, МПК⁷ G 10 L 3/02 от 2000 г.), отличие заключается в том, что инверсия производится только в матрице [E]_Nxm (см. фиг.9). При инвертировании элемента в матрице [Е]_Nxm одновременно инвертируют элементы случайных прямоугольных матриц [Y(k)]_Nxm и [X(k)]_mxN.

Таким образом, представление матрицы нормированных значений двумерного дискретно-косинусного преобразования размером NxN элементов [V(k)]_NxN в цифровом виде на передающей стороне осуществляют на основе генерирования множества нулевых и единичных элементов в виде случайной прямоугольной матрицы размером Nxm (матрица [Е]_Nxm) (см. фиг.7а, 7б) и k - случайных ключевых матриц размером mxN и Nxm элементов (матрица [X_кл(k)]_mxN и [Y_кл(k)]_Nxm) (см. фиг.6в, 6г). Затем данные матрицы преобразуют путем деления элементов каждой строки случайной прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки, т.е. ее вес - v_y(k) (см. книгу: Э.Берлекэмп. Алгебраическая теория кодирования - M.: Мир, 1971, с.12) (см. фиг.7д) и деления элементов каждого столбца случайной прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца, т.е. его вес - v_x. Тем самым формируют матрицы и (см. фиг.7е).

Аналогично способу-прототипу вычисляют результирующую матрицу размером NxN элементов, т.е. путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером Nxm элементов случайной квадратной матрицы размером mxm элементов [B]_mxm и полученной после преобразования прямоугольной матрицы размером mxN элементов (см. фиг.8).

Матрица должна быть наиболее близкой к матрице [V(k)]_NxN по некоторому критерию. Известно (см., например, книгу: У.Претт. Цифровая обработка изображений. Часть 1. - М.: Мир, 1982, с.121-127), что одним из основных объективных критериев близости является среднеквадратическая ошибка. Минимизируя среднеквадратическую ошибку, добиваются минимальных расхождений между матрицами [V(k)]_NxN и Поэтому, рассчитывают сумму квадратов разностей между элементами результирующей матрицы размером NxN элементов и соответствующими им элементами матрицы нормированных значений двумерного дискретно-косинусного преобразования размером NxN элементов [V]_NxN. Затем последовательно инвертируют каждый элемент случайной прямоугольной матрицы размером Nxm элементов (см. фиг.9) и преобразуют их аналогичным образом, как было описано при преобразовании матриц [Y(k)]_Nxm и [X(k)]_mxN (см. фиг.7а, 7б, 7в, 7г, 7д, 7е). Последовательно перемножают полученную после преобразования k-случайных прямоугольных матриц размером Nxm элементов случайную квадратную матрицу размером mxm элементов и полученную после преобразования k-случайных прямоугольных матриц размером mxN элементов.

Поскольку, в матрице [E]_Nxm содержался инвертированный элемент, что после преобразования привело к изменению значений элементов матриц [Y(k)]_Nxm и [X(k)]_mxN и соответственно привело к изменениям матриц и изменяются значения элементов результирующей матрицы Затем для оценки степени приближения матрицы к [V(k)]_NxN повторно рассчитывают k-сумм квадратов разностей между элементами k-результирующих матриц размером NxN элементов и элементами k-матриц нормированных значений двумерного дискретно-косинусного преобразования размером NxN элементов. Затем суммируют полученные k-суммы квадратов разности и вычитают полученную сумму квадратов разности от аналогичной суммы, полученной на предыдущем шаге. В случае положительной разности, т.е. уменьшения среднеквадратической ошибки, сохраняют инвертированное значение элемента, а в противном случае - выполняют его повторную инверсию.

Подобным образом производят инверсию всех битов в матрицы [Е]_NxN и добиваются минимальной среднеквадратической ошибки между матрицами и [V(k)]_NxN, что однозначно указывает на оптимальность сформированных матриц [Y(k)]_Nxm, [X(k)]_mxN и т.е. достижение наилучшего качества при заданном фиксированном объеме передаваемой информации.

Передают множество нулевых и единичных элементов прямоугольных матриц [Е]_Nxm по каналу связи (см. фиг.10). На фигуре 10 знак ⊕ обозначает перемножение матриц.

На приемной стороне принимают из канала связи множество нулевых и единичных элементов прямоугольных матриц [E]_Nxm. Затем вычисляют матрицы [Y(k)]_Nxm и [X(k)]_mxN путем произведения матрицы [E]_Nxm на матрицу [Y_кл(k)]_Nxm и произведения транспонированной матрицы [E]_Nxm на матрицу [X_кл(k)]_mxN соответственно. Затем преобразуют матрицы [Y(k)]_Nxm и [X(k)]_mxN путем деления элементов каждой строки прямоугольной матрицы размером Nxm элементов на сумму единиц соответствующей строки, т.е. ее вес v_y (см. фиг.7е) и деления элементов каждого столбца прямоугольной матрицы размером mxN элементов на сумму единиц соответствующего столбца, т.е. его вес v_x (см. фиг.7д). Тем самым на приемной стороне формируют матрицы и

Формируют матрицу восстановленных нормированных значений двумерного дискретно-косинусного преобразования размером NxN элементов путем последовательного перемножения k-случайных прямоугольных матриц случайной квадратной матрицы [В]_mxm и k-случайных прямоугольных матриц (см. фиг.8).

Для получения восстановленных коэффициентов реальной размерности необходимо произвести операцию денормирования. Учитывая, что на приемной стороне была сформирована нормировочная матрица [С]_NxN, k-матриц восстановленных значений двумерного дискретно-косинусного преобразования размером NxN элементов (в дальнейшем обозначим ее как ) формируют путем деления значения каждого i,j-го элемента матрицы на соответствующий элемент нормировочной матрицы размером NxN элементов (см. фиг.12).

Для восстановления передаваемого сообщения необходимо сформировать k-матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов (в дальнейшем обозначим ее как ). Эту операцию производят путем присвоения значения каждого i,j-го элемента матрицы восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером NxN элементов каждому i,j-му элементу матрицы восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов, а в качестве остальных элементов записывают нули (см. фиг.13).

Далее формируют k-матриц восстановленных квантованных отсчетов неподвижного полутонового видеоизображения путем перемножения транспонированной матрицы дискретно-косинусного преобразования размером МxМ элементов на k-матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером МxМ элементов и на матрицу дискретно-косинусного преобразования размером МxМ элементов (см. фиг.14), т.е. на основании формулы: , где - матрица восстановленных квантованных отсчетов g-го неподвижного полутонового видеоизображения размером МxМ элементов.

На последнем этапе представляют матрицу в виде неподвижного полутонового видеоизображения, присвоив каждому пикселу неподвижного полутонового видеоизображения значение соответствующего элемента матрицы

Для оценки возможности достижения сформулированного технического результата при использовании заявленного способа сжатия и восстановления сообщений было проведено имитационное моделирование на ПЭВМ. Размер случайной квадратной матрицы [B]_mxm составлял 128x128 элементов. Такой размер матрицы [В]_mxm выбран исходя из того, что в качестве исходного сообщения использовано неподвижное полутоновое видеоизображение ра