Способ построения сотовой связи

Способ построения сотовой связи

Иллюстрации

Показать все

Реферат

Способ построения сети сотовой связи относится к системам радиосвязи и может использоваться для оказания услуг электросвязи.

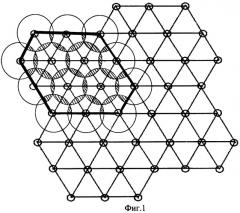
В основе организации систем сотовой связи лежит разделение обслуживаемой территории на микрозоны - соты. См., например, патент США №5418779 по классу H 04 L 12/48 “Архитектура сети с высокоскоростной коммутацией”, геометрия расположения базовых станций (малые кружки) и зоны связи (большие круги) известного устройства приведены на фиг.1.

Из фиг.1 видно, что в известной сотовой системе связи зона обслуживания полностью покрыта сотами, в центре которых размещены базовые станции, расположенные на равном расстоянии друг от друга, образуя правильные треугольники. В районе обслуживания осуществляется управление переключением каналов между радиозонами с таким расчетом, чтобы при переходе подвижного объекта из одной зоны в другую радиообмен мог продолжаться без перерыва. Для этого необходимо осуществить перекрытие зон. Полное покрытие плоской поверхности с помощью правильных многоугольников достигается только в трех случаях: для равносторонних треугольников, квадратов и шестиугольников. Условно геометрию отдельной сотовой ячейки с учетом перекрытия принимают правильным шестиугольником, в центре описанной окружности которого располагается базовая станция. Она является для упомянутых правильных многоугольников оптимальной по критерию минимальной площади перекрытия ячеек (21% от площади высоты, см. книгу Зыкова А.А. Основы теории графов. - М.: Наука, 1987. 381 с.), что предельные (минимальная и максимальная) оценки необходимого числа каналов связи соответствует хроматическому числу ориентированного графа Бержа, характеризующего взаимовлияние радиоэлектронных средств, обслуживающих эти каналы связи. При этом расчет осуществляется с использованием инвариантов ориентированного графа: А - максимальная степень вершин, α - вершинное число независимости, χ - хроматическое число дополнительного графа. Применительно к заявляемой сети сотовой связи, характеризуемой значительным числом секторов базовых станций, анализируемых с позиции их взаимовлияния, оценка максимально необходимого числа частотных каналов М_макс (хроматического числа графа сотовой сети) производится на основе расчета максимальной степени вершин графа Бержа Δ по формуле

Минимально необходимое число частотных каналов М_мин ограничивается “кликой” К, численно равной количеству вершин максимально полного подграфа, выделяемого из графа Бержа

М_мин=К.

В результате вычислений по приведенным двум формулам получены оценки в виде зависимостей минимально и максимально необходимых частотных каналов в зависимости от количества секторов базовой станции, одновременно привлекаемых для обслуживания общей зоны в интересах повышения графика сотовой сети.

Оценки, получаемые с помощью вышеприведенных формул, обеспечивают грубые оценки, так как не учитывают взаимовлияние секторов базовых станций по смежным частотным каналам и через один частотный канал; дополнительных ограничений на использование частотных каналов базовой станции по условиям обеспечения электромагнитной совместимости с радиоэлектронными средствами другого назначения, функционирующими в области энергетической доступности для помех от трансиверов базовых станций. Перечисленные факторы смещают оценки, получаемые с помощью приведенных формул, в сторону их максимизации. Использование приведенных формул показывает, что при расположении базовых станций в вершинах равносторонних пятиугольников достигается увеличение числа каналов в площади сектора S_сек примерно в 1,5 раза по сравнению с расположением базовых станций в вершинах правильных шестиугольников.

Наиболее близким по технической сущности к предлагаемому решению является способ построения сети сотовой связи, описанный в авторском свидетельстве СССР №1626412 А1 по классу Н 04 В 7/26 “Способ радиосвязи с подвижными объектами в системе связи сотовой структуры”, принятый за прототип.

Известная архитектура (геометрия) сотовой связи (фиг.1) состоит из базовых станций, расположенных в вершинах треугольников, а базовые станции управляются с условием, что при переходе подвижного объекта из одной зоны в другую телефонный обмен мог бы продолжаться без перерыва. Регулирование мощности передатчиков проводится на основании измерений и команд подвижных объектов, т.е. по схеме с обратной связью. Для каждого канала прямого трафика мощность регулируют индивидуально. В процессе регулирования мощности базовые станции периодически уменьшают мощность излучения в канале трафика. Мощность понижается до тех пор, пока подвижный объект не зарегистрирует превышение порогового уровня частоты ошибочных кадров и не пошлет запрос на увеличение мощности передатчика базовой станции. Получая команды подвижных объектов, базовые станции повышают мощность излучения в соответствующих каналах графика, при этом она перераспределяет выделенный ей системой и жестко ограниченный ресурс мощности.

Для обеспечения эффективности радиосвязи путем расширения зоны обслуживания при сохранении числа базовых станций в прототипе предлагается круговое сканирование с помощью фазированных антенных решеток, установленных на базовых станциях, куда поступают сигналы от подвижных объектов. Использование фазированных антенных решеток требует запоминания азимутального угла подвижного объекта относительно базовой станции и осуществления соединения с подвижным объектом только во время пересечения главного лепестка диаграммы направленности фазированной антенной решетки базовой станции подвижного объекта. Для нормальной загрузки системы связи требуется равномерное распределение подвижных объектов по азимутальному углу диаграммы направленности, что трудно обеспечить в реальных условиях, это является существенным недостатком способа-прототипа.

Для устранения указанных недостатков в предлагаемом способе построения сотовой связи, заключающемся в продолжении непрерывного радиообмена при переходе подвижной станции из одной зоны обслуживания в другую, согласно изобретению используют базовые станции двух радиусов зон обслуживания, которые располагают в вершинах одинаковых равносторонних пятиугольников с двумя несмежными прямыми углами, покрывающими обслуживаемую территорию без разрывов, причем базовые станции с меньшим радиусом обслуживания располагают в центре пересечения двух взаимно перпендикулярных линий, проходящих через три базовые станции, образуя квадрат.

Заявляемый способ построения сотовой связи основывается на решении задачи оптимального размещения на земной поверхности базовых станций сотовой сети с равномерной (круговой) зоной связи, обеспечивающего минимальное взаимное перекрытие зон связи. При этом зоны связи перекрываются без зазора (без зазоров между зонами связи), чем обеспечивается радиообмен без перерыва. Для этого используем следующий подход. Площадь взаимного перекрытия γ будет определяться по аналитической формуле

где β - смежный угол перекрытия, показанный на фиг.3.

Оптимальное решение отсюда определяется по формуле

cos2β=2cosβ+sinβ, (2)

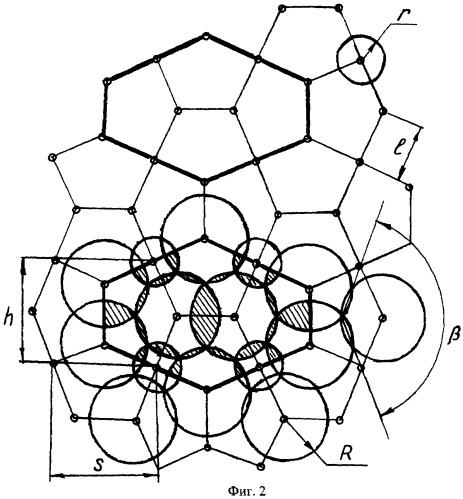
Действительными корнями уравнения (2) будут: β1=-90° и β₂=125,25. Для обеспечения покрытия плоской поверхности равносторонними пятиугольниками без разрывов, если выбраны два угла пятиугольника по 90°, остальными углами будут: 132° (между углами в 90°) и два угла по 114°. Длину стороны равностороннего пятиугольника обозначим через l. Вершины пятиугольника, находящиеся на пересечении взаимно перпендикулярных углов (90°), образуют квадрат со стороной h=s=1,827l (фиг.2). В этих вершинах располагаются базовые станции, обеспечивающие радиус зоны связи 0,4355l, а в вершинах с углами 114° и 132° передатчики с радиусом зоны связи 0,7574l.

Оптимальность выбранной геометрии подтверждается расчетами. Для гексагональных сот (фиг.1) и предложенной геометрии (фиг.2) выделим фрагменты в виде похожих шестиугольников, показанных сплошными жирными линиями. Степень перекрытия определим как отношение площади перекрытия к общей площади, ограниченной сплошными жирными линиями

где - суммарная площадь зон перекрытия, - площадь отдельной зоны перекрытия, S_общ - площадь шестиугольного фрагмента.

Зоны перекрытия () на фиг.1 и фиг.2 показаны в виде областей наложения пересекающихся окружностей и показаны штриховкой. Общая площадь (S_общ) ограничена сплошной толстой линией и представляется в виде шестиугольных фрагментов (фиг.1 и фиг.2), похожих на усеченные ромбы.

Сравним базовый вариант (фиг.1) и новый вариант (фиг.2). Обозначим расстояния между базовыми станциями через l. Нас будет интересовать отношение площадей, поэтому различные значения этого параметра на фиг.1 и фиг.2 не оказывают влияния на результат вычисления по формуле (3). Зоны обслуживания примем имеющими форму круга. Площадь отдельной зоны перекрытия найдем в виде суммы двух сегментов, ограниченных соответствующими дугами.

Базовый вариант.

Рассмотрим базовый вариант, представленный на фиг.1. Как видно, шестиугольный фрагмент содержит 16 равносторонних треугольника, в узлах которых расположены базовые станции. Для обеспечения непрерывного радиообмена (отсутствия промежутков между зонами обслуживания) необходимо иметь радиус зоны обслуживания R=0,577l. При этом площади отдельных треугольников будут S▿=0,144l², а общая площадь фрагмента будет S_общ=2,304l. Одна зона перекрытия имеет площадь =0,061l. Таких зон на фрагменте фиг.1 насчитывается 24. Поэтому суммарное перекрытие внутри фрагмента будет S_пер=1,464l². Подставляя в формулу (3), получим степень перекрытия δ=63,54%.

Новый вариант.

Рассмотрим новый вариант, представленный на фиг.2 и проведем аналогичные расчеты. Площадь одного пятиугольника составляет 1,661l², а суммарная площадь фрагмента, состоящего из 4 пятиугольников, будет S_общ=6,529l².

Зоны перекрытия, как видно из фиг.2, представлены 3 типов:

1) перекрытие двух зон большого радиуса, расстояние между центрами которых равно l. Эта площадь равна =0,397l²;

2) перекрытие двух зон большого радиуса, расстояние между центрами которых равно . Эта площадь равна =0,007l²;

3) перекрытие зоны малого радиуса с зоной большого радиуса. Эта площадь равна =0,0597l².

Суммарная площадь перекрытия фрагмента будет

S_пep=2+8(+)=1,327l².

Отсюда степень перекрытия будет δ=19,97%, т.е. в 3,182 раза меньше, чем у базового варианта.

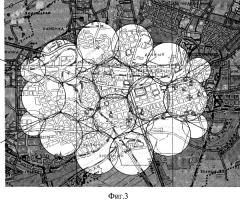
На фиг.3 изображен план местности, охваченной сотовой связью, где базовые станции распределены по вершинам пятиугольников. При покрытии сотовой связью большой (сравнимой с радиусом Земли) и неровной по высоте территории необходимо учитывать дополнительные преимущества заявляемого размещения базовых станций.

Плоскую поверхность возможно покрыть только равносторонними треугольниками, квадратами и правильными шестиугольниками. Однако, учитывая, что земная поверхность близка к сферической, которую можно вписать в додекаэдр (правильный многогранник, составленный из правильных пятиугольников), то при небольшой деформации (изменении внутренних углов) возможно покрытие различных неплоских поверхностей.

В то же время неплоскую поверхность невозможно покрыть правильными шестиугольниками. В этом смысле предлагаемый способ построения сотовой связи имеет преимущество, так как при деформации равносторонних пятиугольников возможно покрытие как плоских, так и неровных и выпуклых поверхностей.

Способ построения сотовой связи, заключающийся в продолжении непрерывного радиообмена при переходе подвижной станции из одной зоны в другую, отличающийся тем, что используют базовые станции двух радиусов зон обслуживания, которые помещают равномерно в вершинах пятиугольников, покрывающих обслуживаемую территорию без разрывов, причем базовые станции с меньшим радиусом зоны обслуживания располагают в вершинах квадратов.