Способ нарезания прямозубой цилиндрической шестерни

Способ нарезания прямозубой цилиндрической шестерни

Иллюстрации

Показать все

Реферат

Изобретение относится к области машиностроения и может быть использовано при нарезании прямозубой цилиндрической шестерни червячной фрезой.

Наиболее близким по технической сущности к заявляемому техническому решению является способ нарезания прямозубой цилиндрической шестерни, при котором червячную фрезу со стружечными канавками перемещают в направлении оси вращения цилиндрической шестерни и сообщают ей вращение, согласованное с вращением шестерни (Литвин Ф.Л., Теория зубчатых зацеплений, М.: Наука, 1968, с 232).

Недостатком известного способа нарезания цилиндрической шестерни является то, что в рабочем зацеплении между зубьями цилиндрической шестерни и плоского колеса плоскоцилиндрической передачи будет работать кромочный контакт, вызывающий повышенный шум и понижающий несущую способность передачи.

Задачей изобретения является создание цилиндрической шестерни плоскоцилиндрической передачи с заостренными зубьями к внешнему радиусу плоского колеса, который является параметром сопряжения поверхностей зубьев плоского колеса и цилиндрической шестерни.

Поставленная задача достигается тем, что в способе нарезания прямозубой цилиндрической шестерни, при котором нарезаемой шестерне сообщают вращение вокруг своей оси, а червячной фрезе, помимо вращательного движения, сообщают поступательное движение в направлении оси шестерни, траектория перемещения фрезы в осевом направлении шестерни осуществляется под углом к оси вращения цилиндрической шестерни, который выбирают из зависимости:

где

коэффициенты, определяющие положение боковых поверхностей зубьев цилиндрической шестерни, причем α - угол зацепления, ϕ₁, ϕ₂ – углы поворота плоского колеса и цилиндрической шестерни, i=ϕ₁/ϕ₂ - передаточное отношение, при этом верхние знаки относятся к правостороннему, нижние - к левостороннему вращению цилиндрической шестерни.

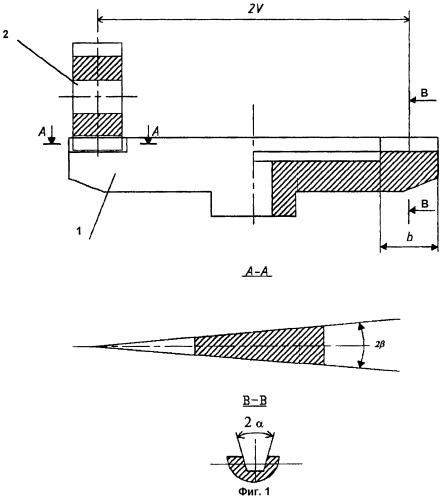
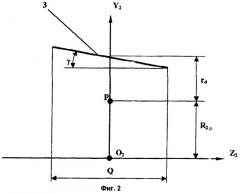
Изобретение поясняется чертежами, где на фиг.1 показана плоскоцилиндрическая передача в рабочем зацеплении, продольное сечение зуба А-А цилиндрической шестерни и торцевое сечение В-В впадины плоского колеса; на фиг.2 представлена схема нарезания цилиндрической шестерни.

Предлагаемый способ нарезания прямозубой цилиндрической шестерни реализован следующим образом.

Плоскоцилиндрическая передача содержит плоское колесо 1 с плоскими рабочими поверхностями и цилиндрическую шестерню 2 с выпуклыми рабочими поверхностями (фиг.1). Середина ширины венца Q (фиг.2) цилиндрической шестерни совмещена со средним диаметром 2V зубчатого венца b плоского колеса. Впадины между зубьями плоского колеса выполнены радиальными, равноширокими и равноглубокими, причем нормальный поперечный профиль сечения впадины В-В образован линиями, образующими угол 2α реечного контура. Зубья цилиндрической шестерни являются прямозубыми и выполнены разновысокими с криволинейным поперечным профилем. В продольном сечении А-А зубья цилиндрической шестерни имеют угол 2β заострения к внешнему радиусу плоского колеса, причем угол заострения зуба цилиндрической шестерни является углом сопряжения зубьев плоского колеса и цилиндрической шестерни.

Геометрические параметры плоскоцилиндрической передачи, а также параметр, определяющий способ нарезания прямозубой цилиндрической шестерни, получают аналитическим путем. Для этого используют три прямоугольные координатные системы, из которых две - подвижные, связанные с плоским колесом и цилиндрической шестерней, и одна неподвижная, относительно которой задаются положения подвижных систем.

Уравнения боковой поверхности зуба плоского колеса - плоскость, заданная уравнением AX+BY+CZ+D=0 (в подвижной системе координат плоского колеса). Уравнения боковых поверхностей зуба цилиндрической шестерни описываются прямыми, полученными от пересечения двух поверхностей первого порядка А₁Х+B₁Y+C₁Z+D₁=0 и А₂Х+B₂Y+C₂Z+D₂=0 (в подвижной системе координат цилиндрической шестерни). Эти линии и плоскость, проходящая через оси вращения ведущего и ведомого колес, определяют угол β сопряжения, который зависит от коэффициентов А_1,2, В_1,2, С_1,2. Задаваясь значением ϕ₁ и имея в виду, что ϕ₂=iϕ₁, и зная кривую линию, по которой описан поперечный профиль цилиндрической шестерни, получены углы наклона линий, описывающих боковую поверхность зуба. (Теория проектирования плоскоцилиндрических передач изложена в работе авторов: О.Л. Подгаевский, Г.В. Жужжалкин. "Проектирование плоскоцилиндрических передач (базовое колесо - плоское колесо)", см. "Вестник машиностроения", 2000, №10, с.38-44.)

При получении заостренного угла 2β в продольном сечении зуба цилиндрической шестерни к внешнему радиусу плоского колеса в полюсе зацепления плоскоцилиндрической передачи также используют уравнения боковых поверхностей зуба цилиндрической шестерни, которые описываются прямыми, полученными от пересечения двух поверхностей первого порядка. Линия, проходящая через полюс зацепления Р плоскоцилиндрической передачи, и плоскость, в которой лежит ось вращения цилиндрической шестерни и которая перпендикулярна оси вращения плоского колеса, определяют угол у наклона траектории перемещения червячной фрезы, который зависит от коэффициентов A_1,2, В_1,2, С_1,2.

Траектория 3 перемещения червячной фрезы (фиг.2) с делительным радиусом r_d в системе координат цилиндрической шестерни наклонена на угол γ к оси вращения Z₂ цилиндрической шестерни со средним радиусом R_2p. Средний радиус цилиндрической шестерни проходит через полюсную точку Р плоскоцилиндрической передачи, которая является средней точкой венца Q цилиндрической шестерни.

Пример расчета угла γ наклона траектории перемещения червячной фрезы к оси вращения цилиндрической шестерни в полюсе зацепления плоского колеса и цилиндрической шестерни.

Исходные данные:

1. Числа зубьев ведущего и ведомого колес соответственно Z_ш=18 и Z_K=216, передаточное отношение i=12, модуль зацепления m=3,9884 мм (рассчитывается на среднем диаметре плоского колеса 2V=861,5 мм), угол поворота цилиндрической шестерни и плоского колеса во время взаимного обката до полюса зацепления соответственно ϕ₂=23,267° и ϕ₁=1,939°, угол зацепления α=20°.

2. Расчетные коэффициенты для полюса зацепления при правостороннем вращении плоского колеса:

A₁=0,998; B₁=-0,057; С₁=0,032;

А₂=-0,711; В₂=-11,962; С₂=0,939.

3. Угол сопряжения зуба цилиндрической шестерни в полюсе зацепления

β=1,566°.

4. Угол наклона траектории перемещения червячной фрезы γ=4,579°.

Предложенный способ нарезания прямозубой цилиндрической шестерни позволит осуществить в полюсной точке плоскоцилиндрической передачи линейно-локализованный контакт между поверхностями зубьев плоского колеса и цилиндрической шестерни.

Способ нарезания прямозубой цилиндрической шестерни, при котором нарезаемой шестерне сообщают вращение вокруг своей оси, а червячной фрезе сообщают вращательное движение и поступательное движение с траекторией, расположенной под углом γ к оси вращения цилиндрической шестерни, отличающийся тем, что величину угла γ выбирают из зависимости

где A₁, A₂, B₁, B₂, C₁, C₂ - коэффициенты, определяющие положение боковых поверхностей зубьев цилиндрической шестерни;

A₁=± cosα cosϕ ₁cosϕ ₂±sinα sinϕ ₂;

B₁=-cosα cosϕ ₁sinϕ ₂+sinα cosϕ ₂;

C₁=cosα sinϕ ₁;

A₂=cosα sinϕ ₁cosϕ ₂i cosα cosϕ ₁sinϕ ₂±i sinα cosϕ ₂;

B₂=cosα sinϕ ₁sinϕ ₂-i cosα cosϕ ₁cosϕ ₂-i sinα sinϕ ₂;

C₂=cosα cosϕ ₁;

α - угол зацепления;

ϕ ₁, ϕ ₂ - углы поворота плоского колеса и цилиндрической шестерни во время взаимного обката до полюса зацепления;

i=ϕ ₁/ϕ ₂ - передаточное отношение;

при этом верхние знаки “+” или “-” относятся к правостороннему, а нижние - к левостороннему вращению цилиндрической шестерни.