Способ бесконтактного измерения координат точек объектов, находящихся в жидкости

Способ бесконтактного измерения координат точек объектов, находящихся в жидкости

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике, а именно к способам измерения длины, ширины и толщины посредством определения координат точек, в частности измерения размеров рыб, и может быть использовано в рыбоводстве для бесконтактного мониторинга ремонтно-маточных рыбных стад.

Известны оптический способ и устройство для контроля количества и формы подводных объектов, в частности рыб, основанных на принципах анализа цифровых изображений и стерео зрения (JP 4329496, G 01 B 11/24, 1992). Способ заключается в том, что рыба перекачивается из одного бассейна в другой через измерительную камеру с прозрачными стенками, через которые стереопара цифровых видеокамер регистрирует изображение перемещаемых рыб, которое анализируется блоком обработки и анализа изображений для измерения рыб и подсчета их количества.

Недостатком известного способа и реализующего его устройства являются низкая точность измерений из-за отсутствия учета преломляющих свойств воды, невозможность измерения рыб среднего и крупного размеров в условиях их естественного содержания, возможность травмирования рыбных особей, длительность и большие энергетические затраты процесса перекачивания воды и рыбы.

Известно устройство для контроля количества и формы подводных объектов, в частности рыб, основанное на принципах анализа цифровых изображений (JP 2157604, G 01 B 11/00, 1990). Способ заключается в том, что на одной из стенок бассейна с рыбами устанавливается многоэлементный источник света, а через противоположную стенку регистрируется изображение с помощью видеопреобразователя, которое обрабатывается в блоке анализа координат.

Недостатком известного устройства являются низкая точность измерений из-за отсутствия учета преломляющих свойств воды, громоздкость многоэлементного осветителя.

Наиболее близким из известных по своей технической сущности и достигаемому результату является способ бесконтактного определения пространственных координат точек объекта, включающий фотографирование объекта из нескольких позиций, опознавание точек изображения объекта на фотографических снимках и вычисление пространственных координат точек объекта, причем на каждом фотографическом снимке измеряют расстояния между опознанными точками и вычисляют пространственные координаты точек объекта (РФ №2173445, G 01 C 11/00, 2001).

Недостатком известного способа является то, что он не обеспечивает требуемой точности измерения координат точек объектов, находящихся в жидкости, так как он не учитывает преломляющих свойств жидкости, в которую погружен объект. Определение координат точек объекта по опорным точкам, расположенным безотносительно к поверхности жидкости, или использование обычных уравнений фотограмметрии приводит к существенным ошибкам определения координат, если объект полностью или частично погружен в преломляющую жидкость.

Задачей предлагаемого способа является разработка нового способа бесконтактного измерения координат точек объектов, погруженных в жидкость, в частности рыб. Учет преломляющих свойств жидкости должен повысить точность проводимых измерений по сравнению со способами, не учитывающими этого фактора. Измерения проводятся для любого размера рыбных особей в условиях их естественного освещения и содержания в бассейнах рыбоводного комплекса, то есть без перекачивания рыб из одного бассейна в другой. Бесконтактный способ позволяет исключить тяжелые ручные операции в процессе измерения средних и крупных рыбных особей.

Такой способ позволяет получать измерительную информацию для любого уровня воды и для интенсивно перемещающихся рыб.

Технический результат: повышение точности измерений за счет учета преломляющих свойств жидкости.

Поставленная задача решается тем, что предлагается способ бесконтактного измерения координат точек объектов, находящихся в жидкости, который включает регистрацию изображения объекта из нескольких позиций, опознавание точек изображения объекта и вычисление пространственных координат точек объекта, причем на поверхность жидкости помещают три опорных контрастных точки, расстояние между которыми фиксировано, затем регистрируют изображение опорных точек и объекта через поверхность жидкости, измеряют координаты опорных точек и точек объекта в системе координат изображения, вычисляют внешние параметры ориентирования изображения относительно поверхности жидкости, вычисляют координаты точек объекта в объектной системе координат, на основе уравнений фотограмметрии, которые учитывают влияние преломляющих свойств жидкости, исходя из формулы:

где h - глубина погружения точки F объекта,

- вектор нормали к поверхности жидкости,

n - показатель преломления жидкости,

- радиус-вектор точки преломления,

(Х_F,У_F) - координаты точки F в плоскости изображения,

f - фокусное расстояние камеры,

- вектор, соединяющий центр проектирования S и точку преломления М,

- единичный вектор луча SM,

- радиус вектор, соединяющий начало объектной системы координат и центр проекции S,

- касательная составляющая единичного вектора падения у поверхности воды,

Аr_i - вектор, соответствующий i-той строке матрицы А, то есть,

X_S, Y_S, Z_S - линейные элементы внешнего ориентирования,

ψ, θ, γ - угловые элементы внешнего ориентирования,

- радиус-вектор точки F объекта.

Сущность способа состоит в том, что расположение опорных точек на поверхности жидкости позволяет определить параметры ориентирования камер относительно ее поверхности, предложенные уравнения фотограмметрии позволяют учесть преломляющие свойства жидкости на основе определенных параметров внешнего ориентирования камер. Учет преломляющих свойств жидкости, обуславливающих смещение на изображении точек, находящихся в жидкости, позволяет устранить методическую ошибку измерений координат этих точек. Предложенный способ устраняет эту методическую ошибку измерений, и это, в свою очередь, повышает точность измерений координат точек объекта, находящегося в жидкости.

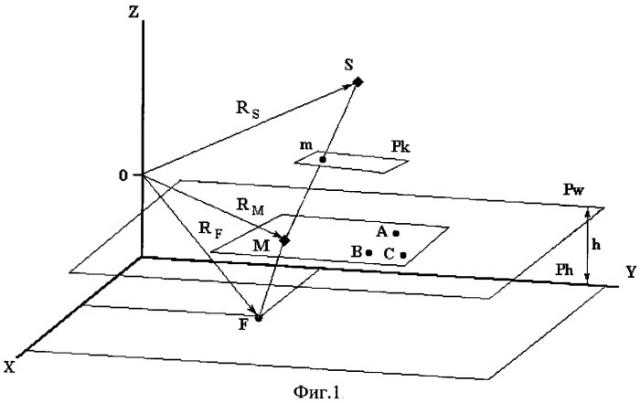
На фиг.1 изображена геометрия расчетной модели.

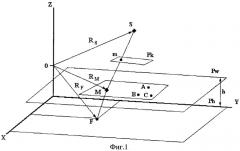
На фиг.2 показан процесс обработки и анализа изображения опорных точек и объектов-рыб.

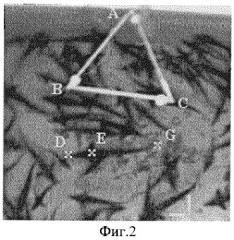
На фиг.3. отображен процесс измерения рыб в бассейне рыбоводного комплекса.

На фиг.4. приведена одномоментная стереопара изображений бассейна с рыбами и контрастными опорными точками.

Способ осуществляется следующим образом. Помещают три опорных контрастных точки А, В, С (фиг.1) на поверхность жидкости, - расстояние между которыми известно (то есть измерено обычными средствами измерения длины) и жестко зафиксировано. Если уровень жидкости изменяется, то соответственно должно измениться и положение опорных точек А, В, С. В качестве приспособления для таких опорных контрастных точек целесообразно использовать светодиоды, размещенные в вершинах равностороннего треугольника (фиг.2), который должен обладать свойством плавучести. Стороны треугольника изготавливают из жесткого материала, так как они фактически являются эталонами длины на каждом изображении. Поперечное сечение сторон треугольника должно быть минимальным, чтобы они не заслоняли элементы измеряемого объекта. Регистрируют изображения опорных точек и объекта, погруженного в преломляющую среду - для этого камера должна быть ориентирована так, чтобы в поле зрения одновременно попадали и опорные точки А, В, С и измеряемый объект. Центр проектирования S (фиг.1) и изображение точки объекта m, лежащее в плоскости изображения Pk, позволяют построить траекторию падающего луча SM, где М - точка преломления, находящаяся на поверхности жидкости Pw. Преломленный луч MF соединяет точку преломления М и точку измеряемого объекта F, находящуюся в жидкости на глубине h в плоскости Ph. Камера должна быть предварительно откалибрована, то есть должны быть определены: f - фокусное расстояние, координаты главной точки кадра (x₀, у₀). Начало координат изображения будем считать находящимся в главной точке. Измеряют координаты опорных точек и точек объекта в системах координат изображения - каждая точка на изображении имеет две координаты. Вычисляют внешние параметры ориентирования изображений относительно поверхности преломляющей жидкости. Для этого используют измеренные координаты опорных точек А, В, С на снимке (х_i, у_i) и в объектной системе координат (X_i, Y_i, Z_i), где i{1,2,3}. Начало координат объектной системы координат целесообразно поместить в одну из опорных точек, ось абсцисс провести через вторую опорную точку, а вертикальную ось координат Z полагать перпендикулярной, к плоскости, в которой расположены опорные точки, то есть к поверхности жидкости. В таком случае, для решения стоящей задачи будет достаточно информации о расстоянии между опорными точками, а точное положение треугольника с опорными точками будет не нужно. Линейные и угловые элементы внешнего ориентирования X_S, Y_S, Z_S, ψ, θ, γ определяются из следующей известной системы уравнений (РФ №2173445, G 01 C 11/00, 2001):

где R_i=(X_i,Y_i,Z_i)^T - радиус-вектор, соединяющий начало объектной системы координат и i-тую опорную точку,

R_S=(X_S,Y_S,Z_S)^T - радиус-вектор, соединяющий начало объектной системы координат и центр проекции S,

Ас_i - вектор, соответствующий i-тому столбцу матрицы А, определяющей преобразование системы координат при повороте на углы ψ,θ,γ,

то есть А=(Ас₁ Ас₂ Ас₃).

Данная система имеет 6 неизвестных и столько же уравнений, то есть является определенной. Вычисляют координаты точек объекта в объектной системе координат на основе уравнений фотограмметрии, которые учитывают влияние преломляющих свойств жидкости. Искомые координаты точки F измеряемого объекта вычисляют исходя из формулы:

где h - глубина погружения точки F объекта,

- вектор нормали к поверхности жидкости,

n - показатель преломления жидкости,

- радиус-вектор точки преломления,

(х_F,у_F) - координаты точки F в плоскости изображения,

f - фокусное расстояние камеры,

- вектор, соединяющий центр проектирования S и точку преломления М,

- единичный вектор луча SM,

- радиус-вектор, соединяющий начало объектной системы координат и центр проекции S,

- касательная составляющая единичного вектора падения у поверхности воды,

Аr_i - вектор, соответствующий i-той строке матрицы А, то есть

A=(Ar₁ Ar₂ Ar₃)^T

X_S, Y_S, Z_S - линейные элементы внешнего ориентирования,

ψ, θ, γ - угловые элементы внешнего ориентирования,

- радиус-вектор точки F объекта.

Таким образом, получены искомые координаты точки объекта F, находящейся в жидкости.

Пример.

Проводились измерения длин рыб, находящихся в бассейне рыбоводного комплекса. Для проведения измерений была развернута измерительная система (фиг.3). В состав системы входили: 1 - две цифровые видеокамеры, 2 - контрастные метки на поверхности воды, 3 - ЭВМ для обработки изображений, 4 - передвижной штатив, 5 - бассейн с рыбами.

На поверхность воды помещают три опорных точки, реализованных в виде приспособления. Это приспособление представляет собой три светодиода, размещенных в вершинах треугольника, обладающего плавучестью.

Изображения объекта и опорных точек одномоментно регистрируют двумя цифровыми камерами CVR-PC1-USB-RP. Разрешение камер 640×480 пикселов, фокусное расстояние 50 мм. С помощью специального штатива камеры располагались над центральной частью бассейна. Высота возвышения составляла от 2 до 5 метров, что зависело от размеров бассейна. Полученная стереопара приведена на фиг.4. Фрагмент одного из изображений увеличен и приведен на фиг.2.

Измеряют координаты опорных точек А, В, С и точек объекта D, E, G в системе координат двух цифровых изображений (х1,у1) и (х2,у2). Результаты измерений приведены в таблице 1.

Таблица 1.
Точка	х1 (пиксел)	у1 (пиксел)	х2(пиксел)	у2(пиксел)
А	498	73	259	31
В	451	150	197	106
С	548	152	297	118
D	428	220	196	179
Е	452	215	220	177
G	515	204	287	169

Вычисляют внешние параметры ориентирования изображений относительно поверхности жидкости. Начало объектной системы координат помещено в точку В, ось абсцисс направлена из точки В в точку С. Результаты вычислений:

для первой камеры X_S=-578 мм, Y_S=-1580 мм, Z_S=4615 мм, ψ=-1.5°, θ=-0.9°, γ=-13.2°,

для второй камеры X_S=813 мм, Y_S=-1506 мм, Z_S=4403 мм, ψ=-7.2°, θ=0.1°, γ=-11.6°.

Вычисляют координаты точек объекта в объектной системе координат, на основе уравнений фотограмметрии, которые учитывают преломляющие свойства воды (n=1.33). Результаты вычислений приведены в таблице 2.

Таблица 2.
Точка	Х (мм)	У (мм)	Z (мм)
D	-58	-218	-854
Е	84	-184	-815
G	456	-110	-817

Длина рыбы определяется как сумма длин звеньев ломаной линии, проведенной по средней продольной линии изображения рыбы. В рассматриваемом примере ломаная линия соединяет точки: D-E-G. Применяются полученные координаты для определения, для измерения длины рыбы, находящейся в естественном состоянии. Длина рыбы в данном случае составила 520 мм. Проверка точности способа проводилась путем сравнения с результатами, полученными прямыми измерениями рыб в процессе их пересадки в соседний бассейн. Результаты измерений приведены в таблице 3.

Таблица 3.
№ рыбы	Измерения предлагаемым способом (мм)	Измерения линейкой (мм)
1	595	570
2	588	580
3	600	600
4	630	600
5	630	600
6	655	630
7	665	640
8	671	640
9	673	650
10	698	650
11	701	670
12	711	680
13	733	710
14	742	710
15	747	710
16	751	780
17	761	790
18	771	790
19	839	810
20	856	810
	Среднее: 701	Среднее: 681

Если считать, что ошибки измерений подчинены нормальному закону распределения, то статистический анализ экспериментальных данных позволяет утверждать, что доверительной вероятности 0.95 соответствует ошибка измерений не более 37 мм (Новицкий П.В., Зограф И.А. Оценка погрешностей измерений. - Л.: Энергоатомиздат, 1991, с.143-144).

Проверка способа была осуществлена на рыбоводном комплексе Волжской ГЭС, основу которого составляет 44 бассейна трех типовых размеров, в которых содержится ремонтно-маточное стадо численностью более 5000 особей. Повышение точности измерений и исключение ручных операций измерения размеров рыб за счет внедрения предлагаемого способа позволит более эффективно реализовать технологический цикл выращивания рыб.

Способ бесконтактного измерения координат точек объектов, находящихся в жидкости, согласно которому регистрируют изображение объекта из нескольких позиций, опознают точки изображения объекта и вычисляют пространственные координаты точек объекта, отличающийся тем, что на поверхность жидкости помещают три опорные контрастные точки, расстояние между которыми фиксировано, затем регистрируют изображение опорных точек и объекта через поверхность жидкости, измеряют координаты опорных точек и точек объекта в системе координат изображения, вычисляют внешние параметры ориентирования изображения относительно поверхности жидкости, вычисляют координаты точек объекта в объектной системе координат на основе уравнений фотограмметрии, которые учитывают влияние преломляющих свойств жидкости исходя из формулы

где h - глубина погружения точки F объекта,

- вектор нормали к поверхности жидкости,

n - показатель преломления жидкости,

- радиус вектор точки преломления,

(х_F,y_F) - координаты точки F в плоскости изображения,

f - фокусное расстояние камеры,

- вектор, соединяющий центр проектирования S и точку преломления М,

- единичный вектор луча SM,

- радиус-вектор, соединяющий начало объектной системы координат и центр проекции S,

- касательная составляющая единичного вектора падения у поверхности воды,

Аr_i - вектор, соответствующий i-й строке матрицы А, то есть

A=(Ar₁ Ar₂ Ar₃)^T,

X_S, Y_S, Z_S - линейные элементы внешнего ориентирования,

ψ, θ, γ - угловые элементы внешнего ориентирования,

- радиус-вектор точки F объекта.