Способ определения местоположения абонентской мобильной станции
Иллюстрации
Показать всеИзобретение относится к области радиолокации и может быть использовано в сотовых системах связи для определения местоположения мобильной станции (МС). Задача, которую решает предлагаемый способ, - повышение точности и надежности определения местоположения абонентской МС. В предлагаемом способе, в отличие от уже известных способов, предлагается не удалять измерения спутников, содержащих аномальные ошибки, а уменьшать вес этих ошибочных измерений и затем искать заново местоположение абонентской МС с использованием скорректированных весовых коэффициентов. Данная операция выполняется до тех пор, пока сумма взвешенных мер ошибок, соответствующих скорректированному местоположению абонентской МС, с использованием уточненных весовых коэффициентов не станет меньше порога. Полученная таким образом скорректированная оценка местоположения абонентской МС принимается за окончательную оценку местоположения абонентской МС. 2 з.п. ф-лы, 5 ил.
Реферат
Предлагаемое изобретение относится к области радиолокации и может быть использовано в сотовых системах связи для определения местоположения мобильной станции (МС).
Постоянное повышение качества и расширение сферы услуг в системах сотовой мобильной связи делает особенно актуальным решение задачи определения местоположения абонентской МС.
Данная задача имеет очень широкий спектр применения. Определение местоположения МС (локация) необходимо для нахождения пользователей, нуждающихся в медицинской, полицейской или другой помощи, для осуществления диспетчерских функций парка машин, например, ″ скорой помощи″ или такси, для специальных полицейских или военных целей и др. Одним из распространенных способов локации является способ с использованием спутниковых навигационных систем, среди которых наиболее распространенной является система Global Positioning System (GPS) (GPS SPS Signal Specification, June 2, 1995, 2nd Edition)[1]. GPS - это система передатчиков спутниковых сигналов, которые передают информацию, на основе которой можно определить местоположение наблюдателя. Полностью действующая GPS включает в себя более 21 спутников Земли, приблизительно равномерно расположенных по шести круговым орбитам, по четыре спутника на каждой, орбиты находятся под углом 55 градусов относительно экватора и отделены друг от друга кратными 60 градусам долготы. Орбиты имеют радиус 26,560 км и приблизительно круговые. Период обращения одного спутника вокруг Земли составляет 11,967 часов. Система GPS рассчитана таким образом, что минимум четыре спутника GPS видны из самых удаленных точек на поверхности Земли. Это позволяет использовать GPS систему для определения положения наблюдателя в любом месте Земли. На каждом спутнике находятся цезиевые или рубидиевые атомные часы, обеспечивающие синхронизацию сигналов, переданных спутниками. В GPS системе осуществляется постоянный контроль за ходом часов на спутниках и в случае необходимости осуществляется коррекция часов для каждого спутника.
Каждый спутник GPS непрерывно передает навигационные сигналы. В передаваемых сигналах содержится информация о том, когда этот сигнал был передан, какие координаты спутника были в данные момент и т.д. Расстояние между спутником и GPS приемником может быть определено посредством измерения временной задержки между временем приема сигнала на GPS приемнике и временем, когда этот сигнал был передан спутником. GPS приемник генерирует такой же сигнал, как и спутник, благодаря чему GPS приемник может оценить временную задержку между сигналами. Но так как часы GPS приемника не точно синхронизированы с атомными часами на спутники, то GPS приемник оценивает псевдорасстояния.
Наиболее часто прием сигналов во время локации осуществляется в городских условиях, в связи с чем большинство измерений псевдорасстояний будут содержать ошибки, связанные с непрямым распространением сигналов в городских условиях.
Поэтому возникает задача определения того, измерения каких спутников содержат аномально большие ошибки, т.е. ошибки, которые могут приводить к большим погрешностям в определении местоположения. Другой не менее важной задачей является задача уменьшения влияния этих измерений на окончательную оценку местоположения МС.
Решение этих задач необходимо для увеличения точности определения местоположения МС.
Один из способов определения спутников с аномально большими ошибками и уменьшения влияния этих измерений на окончательную оценку местоположения описан в патенте US N№5,841,399 "Fault Detection and Exclusion Used in a Global Positioning System GPS Receiver" J. Yu, H 04 B 7/185; G 01 S 5/02, Nov. 24, 1998 [2].
В патенте [2] предлагается в процессе локации составить взвешенную сумму мер ошибок измерений расстояний от всех БС, причем за меру ошибки принять квадрат разности между измеренным расстоянием и расстоянием до предполагаемого местоположения МС. Находят местоположение МС, соответствующее минимуму взвешенной суммы мер ошибок, использующей измерения всех базовых станций (БС), и сравнивают ее значение с порогом, по которому принимают решение о наличии ошибочных измерений. Если будет принято решение о наличии ошибок, то составляют для каждой БС взвешенную сумму мер ошибок от всех БС, кроме данной. Для каждой суммы находят местоположение МС, соответствующее минимуму для данной суммы. Затем находят среди множества данных взвешенных сумм минимальную и сравнивают ее с порогом. Данные операции повторяются до тех пор, пока взвешенная сумма не окажется меньше порога, тогда полученные координаты МС принимают за окончательные или принимают решение о том, что локация не удалась.
Недостатком такого решения является невозможность достоверного обнаружения ошибочных измерений в случае, когда два или более измерений псевдорасстояний содержат аномальные ошибки, что очень характерно в случае локации в городских условиях. В случае, когда аномальные ошибки содержаться в двух или более измерениях, может сложиться ситуация, когда удаление одного неошибочного измерения приведет к тому, что значение взвешенной суммы ошибок не превысит порог, тогда данная оценка местоположения будет принята за окончательную, что приведет к увеличению ошибки в оценке местоположения.
Наиболее близким к заявляемому решению является способ, описанный в патенте US №5,831,576 “Integrity Monitoring of Location and Velocity Coordinates from Differential Satellite Positioning System Signals, H 04 B 7/185; G 01 S 5/02, Nov. 3, 1998 [3].
Такой способ локации заключается в том, что:
1) принимают N сигналов локации, соответствующих каждой из N БС;
2) по принятым сигналам локации оценивают псевдорасстояния от МС до каждой из N БС;
3) для каждой БС определяют меру ошибки по оцененному псевдорасстоянию до МС как квадрат разности между суммой оцененного псевдорасстояния с предполагаемым рассогласованием часов и расстоянием до предполагаемого местоположения МС;
4) для каждой БС определяют весовой коэффициент меры ошибки;
5) суммируют взвешенные меры ошибки;
6) сравнивают взвешенные меры ошибки с порогом;
7) за начальное местоположение МС принимают то, для которого сумма взвешенных мер ошибок минимальна;
8) если сумма взвешенных мер ошибок, соответствующая начальному местоположению МС, больше порога, определяют разность между двумя максимальными взвешенными мерами ошибок, соответствующими начальному местоположению МС;
9) если разность между двумя максимальными взвешенными мерами ошибок, которые соответствуют начальному местоположению МС, превышает порог, то из суммы взвешенных мер ошибок исключают взвешенную меру ошибки, которая соответствует спутнику с максимальной взвешенной мерой ошибки;
10) в качестве окончательной оценки местоположения МС принимают то, для которого сумма взвешенных мер ошибок минимальна.
Согласно данному способу для определения местоположения используются сигналы навигационных спутниковых систем. Одной из основных особенностей навигационных спутниковых систем является точная синхронизация передаваемых сигналов. Это позволяет оценить расстояния до спутников посредством измерения временных задержек между временем передачи сигналов от спутников и временем приема данных сигналов на МС. Но даже при отсутствии ошибок в измерениях временных задержек, в связи с неточной синхронизацией часов МС и глобального времени навигационной спутниковой системы, вычисленные расстояния не будут совпадать с истинными расстояниями от спутника до МС. Расстояния, полученные в результате оценки временных задержек сигналов (псевдорасстояния), будут отличаться от истинных расстояний на одинаковое неизвестное значение, равное временному рассогласованию часов МС, и глобального времени навигационной спутниковой системы, умноженному на скорость света. Тогда расстояние от МС до спутника будет представлять сумму из псевдорасстояния pri до этого спутника и неизвестного рассогласования часов τ , умноженного на скорость света:
rangei=pri+τ · c, где i∈ [1,N] (1)
На основании выше сказанного для каждого спутника может быть сформировано уравнение следующего вида:
pri+τ · c=, i∈ [1,N] (2)
где - {xi,yi,zi}, - координаты i-го спутника. Таким образом составляется система из N уравнений. Решением данной системы уравнений является оценка местоположения МС и оценка временного рассогласования часов МС и глобального времени навигационной спутниковой системы. Для решения подобной переопределенной системы применяется метод наименьших квадратов, а именно для каждого спутника формируется мера ошибки между оцененным расстоянием до спутника и расстоянием между спутником и предполагаемым местоположением МС {x, y, z}
, i∈ [1,N] (3)
Суммарная мера ошибок измерений для всех спутников определяется как взвешенная сумма квадратов значений мер ошибок, сформированных для каждого спутника,
где σ
| 2 |
| i |
За оценку местоположения МС принимается такая точка , в которой функция (4) достигает своего абсолютного минимума. В описываемом способе минимум функции (4) ищется методом Ньютона. Для обнаружения аномально больших ошибок, в рассматриваемом способе предлагается значение функции F(x,y,z,τ ) (4) в точке сравнить с порогом hFA. Значения порога для различных значений вероятности ложной тревоги РFA и количества степеней свободы, определяемых как μ =N-4, приведены в рассматриваемом патенте. Значение вероятности ложной тревоги РFA задается исходя из требований к системе локации.
Если значение функции F в найденной точке минимума не превышает порог hFA, то координаты берутся за окончательную оценку местоположения. В противном случае считается, что в измерениях псевдорасстояний содержатся аномальные ошибки, которые могут привести к большим ошибкам в оценке местоположения. Для определения, в каком именно измерении псевдорасстояния содержатся аномальные ошибки, формируют взвешенные меры ошибок для каждого спутника следующим образом:
i∈ [1,N] (5)
где Si,i -диагональные элементы матрицы S.
Затем находятся две максимальные взвешенные меры ошибок , , и формируется разность
Δ res=-, (6)
которая сравнивается с порогом:
где и - вероятности того, что взвешенные меры ошибок для спутников J1 и J2 примут соответствующие значения и . Если разность (6) больше порога (7), т.е.
то из системы уравнений, применяемой для нахождения оценки местоположения МС, удаляются измерения. J1 спутника и операции, описанные выше, повторяются еще раз. В противном случае считается, что невозможно обнаружить аномальные ошибки в данном наборе измерений, и полученные координаты берутся за окончательную оценку местоположения МС.
Данное изобретение позволяет для случаев, когда величина ошибки в одном измерении псевдорасстояния намного превосходит величины ошибок в остальных измерениях псевдорасстояний, успешно обнаружить в каком из измерений содержится данная ошибка и удалить измерения данного спутника из системы уравнений, которая используется для нахождения оценки местоположения МС.
Однако данное изобретение имеет несколько существенных недостатков.
Исключение измерений спутника из системы уравнений может привести к существенному увеличению геометрического фактора GDOP (Geometric Dilution of Precision), т.е. ухудшению точности ("Сетевые спутниковые радионавигационные системы", 2-е изд., переработанное и дополненное под ред. проф. B.C.Шебшаевича. "Радио и связь", М., 1993) [4]. За счет этого может значительно возрасти среднеквадратичное отклонение оценки местоположения (СКО). В результате, действительная ошибка может оказаться гораздо больше, чем при оценке местоположения с использованием измерений спутника, содержащего аномально большую ошибку.
Наиболее часто определения местоположения МС происходит в городских условиях, в связи с чем аномально большие ошибки, вызываемые многолучевым распространением сигнала, могут содержаться в нескольких измерениях псевдорасстояния. Это может привести к тому, что значения несколько взвешенных мер ошибок будут примерно одинаковыми и
тогда согласно описанному способу определения местоположения для оценки местоположения МС или будут использоваться измерения, содержащие аномальные ошибки, что отрицательно скажется на точности оценки местоположения, или будет дан отказ в локации, что недопустимо в некоторых условиях.
Задача, которую решает предлагаемый способ, - повышение точности и надежности определения местоположения абонентской МС.
Для решения этой задачи в способ определения местоположения абонентской МС, заключающийся в том, что принимают N сигналов локации, соответствующие каждой из N БС, по принятым сигналам локации оценивают псевдорасстояния от МС до каждой из N БС, для каждой БС определяют меру ошибки по оцененному псевдорасстоянию до абонентской МС, для каждой БС определяют весовой коэффициент меры ошибки, суммируют взвешенные меры ошибки и сравнивают их с порогом, за начальное местоположение абонентской МС принимают то, для которого сумма взвешенных мер ошибок минимальна,
дополнительно введены следующие операции:
- если сумма взвешенных мер ошибок, соответствующих начальному местоположению абонентской МС, больше порога, то уточняют весовые коэффициенты мер ошибок таким образом, что,
- для БС, для которых взвешенная мера ошибки, соответствующая начальному местоположению абонентской МС, меньше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок оставляют без изменения,
- для БС, для которых взвешенная мера ошибки, соответствующая начальному местоположению абонентской МС, больше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок уменьшают,
- корректируют местоположение МС с использованием уточненных весовых коэффициентов,
- определяют сумму взвешенных мер ошибок, соответствующих скорректированному местоположению абонентской МС, с использованием уточненных весовых коэффициентов,
- если сумма взвешенных мер ошибок, соответствующих скорректированному местоположению абонентской МС, больше порога, уточнение весовых коэффициентов мер ошибок и коррекцию местоположения абонентской МС продолжают до тех пор, пока сумма взвешенных мер ошибок не станет меньше порога,
- за окончательную оценку местоположения абонентской МС принимают то, для которого сумма мер ошибок, взвешенных уточненными весовыми коэффициентами минимальна.
Меру ошибки по оцененному псевдорасстоянию до абонентской МС определяют как квадрат разности между суммой оцененного псевдорасстояния с предполагаемым рассогласованием часов и расстоянием до предполагаемого местоположения абонентской МС.
Весовые коэффициенты мер ошибок уменьшают, нормируя их на взвешенные меры ошибок.
Сопоставительный анализ способа определения местоположения МС с прототипом показывает, что предлагаемое изобретение существенно отличается от прототипа, так как позволяет повысить точность и надежность определения местоположения абонентской МС.
Сопоставительный анализ заявляемого способа с другими техническими решениями в данной области техники не позволил выявить признаки, заявленные в отличительной части формулы изобретения.
Графические материалы, используемые для пояснения предлагаемого решения.
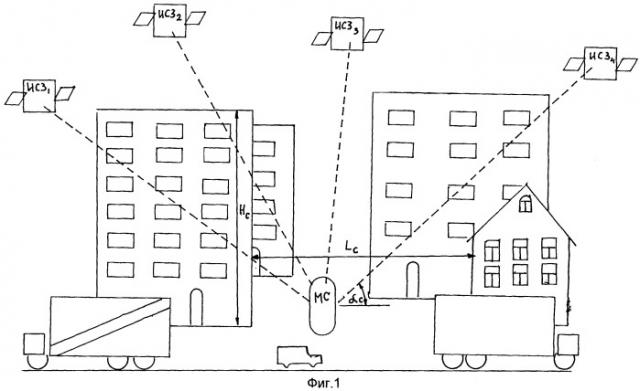
Фиг.1 - рисунок, отражающий информацию о характере застройки в районе, где осуществляется локация.
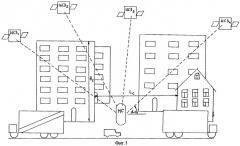
Фиг.2 - рисунок сети сотовой связи, включающей в себя МС и БС.
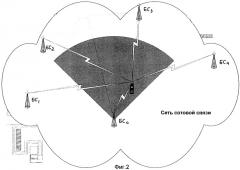
Фиг.3 - пример структурной схемы для реализации предложенного способа.
Фиг.4 - вариант выполнения блока формирования оценок координат МС.
Фиг.5 - рисунок, качественно иллюстрирующий связь оценки вероятности наличия аномальной ошибки, характеристик застройки района и угла возвышения спутника.
Предлагаемый способ заключается в следующем:
1) принимают N сигналов локации, соответствующих каждой из N БС;
2) по принятым сигналам локации оценивают псевдорасстояния от МС до каждой из N БС;
3) для каждой БС определяют меру ошибки по оцененному псевдорасстоянию до МС как квадрат разности между суммой оцененного псевдорасстояния с предполагаемым рассогласованием часов и расстоянием до предполагаемого местоположения МС;
4) для каждой БС определяют весовой коэффициент меры ошибки;
5) суммируют взвешенные меры ошибки;
6) сравнивают взвешенные меры ошибки с порогом;
7) за начальное местоположение МС принимают то, для которого сумма взвешенных мер ошибок минимальна;
8) если сумма взвешенных мер ошибок, соответствующих, начальному местоположению МС, больше порога, уточняют весовые коэффициенты мер ошибок следующим образом:
а) для БС, для которых взвешенная мера ошибки, соответствующая начальному местоположению МС, меньше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок оставляют без изменения,
b) для БС, для которых взвешенная мера ошибки, соответствующая начальному местоположению МС, больше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок уменьшают,
с) корректируют местоположение МС с использованием уточненных весовых коэффициентов,
d) определяют сумму взвешенных мер ошибок, соответствующих скорректированному местоположению МС, с использованием уточненных весовых коэффициентов,
е) если сумма взвешенных мер ошибок, соответствующих скорректированному местоположению МС, больше порога, уточнение весовых коэффициентов мер ошибок и коррекцию местоположения МС продолжают, в соответствии с п.8-a-8-d, до тех пор, пока сумма взвешенных мер ошибок не станет меньше порога,
9) в качестве окончательной оценки местоположения МС принимают то, для которого сумма мер ошибок, взвешенных уточненными весовыми коэффициентами, минимальна.
В предлагаемом способе определения местоположения под термином БС имеются в виду спутники, наземные БС, различные наземные излучатели спутниковых сигналов и сигналов БС, а также различные их комбинации. Одной из основных особенностей навигационных спутниковых систем, как и систем сотовой связи CDMA (системы с множественным доступом с кодовым разделением каналов), является точная синхронизация передаваемых сигналов. Это позволяет оценить расстояния до спутников посредством измерения временных задержек между временем передачи сигналов от спутников и временем приема данных сигналов на МС.
На фиг.1 и фиг.2 изображена ситуация, которая возможна при локации в городских условиях. Данные рисунки иллюстрируют, каким образом могут быть расположены спутники и окружающие здания вокруг МС, возможную конфигурацию сети сотовой связи, а также какая информация доступна о характере застройки в районе, где осуществляется локация.
Однако даже при отсутствии ошибок в определении расстояния, связанных с шумом, федингом и многолучевостью, в связи с неточной синхронизацией часов МС и глобального времени навигационной спутниковой системы, вычисленные расстояния не будут совпадать с истинными расстояниями от спутника до МС. А будут отличаться на одинаковое неизвестное значение, равное временному рассогласованию часов МС и глобального времени навигационной спутниковой системы, умноженному на скорость света. Тогда расстояние от МС до спутника будет представлять сумму из псевдорасстояния (pri) до этого спутника и неизвестного рассогласования часов (τ ), умноженного на скорость света,
rangei=pri+τ · c, где i∈ [1,N]. (9)
Для каждого спутника формируется мера ошибки между расстоянием до спутника, равным сумме псевдорасстояния и предполагаемого рассогласования часов τ , умноженного на скорость света, и фактическим расстоянием между спутником и предполагаемыми координатами МС {x,y,z}
i∈ [1,N] (10)
где – {xi,yi,zi} координаты i-го спутника.
Суммарная мера ошибок измерений для всех спутников определяется как взвешенная сумма квадратов значений мер ошибок, сформированных для каждого спутника
где W - веса, которые устанавливаются исходя из точности измерения псевдорасстояния для каждого спутника. Чем выше точность измерения псевдорасстояния, тем с большим весом данное измерение входит в функцию (11).
За оценку местоположения МС принимается такая точка , в которой функция (11) достигает своего абсолютного минимума.
Минимум функции (11) может быть найден известными математическими методами, например градиентным методом, описанным в справочнике Г. Корн, ″ Справочник по математике″ , М., 1996 [5].
Если предположить, что измерения псевдорасстояний для спутников содержат только независимые ошибки, описываемые гауссовским законом распределения с нулевыми математическими ожиданиями и дисперсиями Di=σ
| 2 |
| i |
pri=pr
| 0 |
| i |
где pr
| 0 |
| i |
Di=σ
| 2 |
| i |
и в качестве весового коэффициента, в формуле (11), взять величину, обратную дисперсии данной ошибки, т.е.
то тогда в точке оценки положения МС распределение случайной величины будет описываться распределением "хи-квадрат" с N-4 степенями свободы (Brown, R.G., "Receiver Autonomous Integrity Monitoring", in "Global Positioning System: Theory and Applications, Volume 2", eds. B.W. Parkinson and J.J. Spilker Jr., American Institute of Aeronautics and Astronautics, 1996 [6]). Этот факт можно использовать для обнаружения аномальных ошибок в измерениях псевдорасстояний. В большинстве случаев прием навигационных сигналов происходит в городских условиях, в связи с чем большинство измерений псевдорасстояний содержат ошибки, обусловленные многолучевым распространением сигнала, шумом и федингом. Поэтому полученные значения могут не совпадать с истинным местоположением МС {x0,y0,z0}. Ошибки в измерениях псевдорасстояний, обусловленные шумом, описываются гауссовским законом распределения с нулевым математическим ожиданием. Такие ошибки будем называть нормальными. Аномальными будем называть ошибки, обусловленные многолучевым распространением сигнала. Наличие аномальных ошибок в измерениях псевдорасстояний можно определить способом, описанным в [6]. Для обнаружения наличия аномальных ошибок значение функции (11) в точке сравнивается с порогом hFA. Порог hFA может быть найден из трансцендентного выражения
где РFA - вероятность того, что при превышении порога ошибки в измерениях псевдорасстояний будут только нормальными. Значение РFA задается исходя из требований к системе локации.
Если значение функции в найденной точке минимума не превышает порог hFA, то считается, что ошибка в оценке местоположения МС обусловлена только наличием гауссовских ошибок, и координаты берутся за окончательную оценку местоположения. В противном случае считается, что в измерениях псевдорасстояний содержаться аномальные ошибки, которые могут привести к большим ошибкам в оценке местоположения. В случае превышения значением порога hFA необходимо определить в каких из измерений псевдорасстояний содержатся аномальные ошибки и при возможности уменьшить влияние данных ошибок на окончательную оценку местоположения. В данном методе предлагается решить эту задачу следующим образом. Значения взвешенных квадратов ошибок для каждого спутника, определяемые следующим образом:
resi=Wif
| 2 |
| i |
сравниваются с порогом
Если значения взвешенного квадрата ошибки (15) для данного спутника превышает порог (16), то значение весового коэффициента, соответствующего данному спутнику, изменяется следующим образом:
i∈ [1,N]. (17)
Затем ищется новая оценка местоположения, т.е. минимум функции (11), с использованием новых весовых коэффициентов (17). Процедура, описанная выше, повторяется до тех пор, пока значение функции (11) в точке минимума не станет меньше порога hFA.
Полученные таким образом координаты берутся за окончательную оценку местоположения МС.
Процесс локации может быть выполнен с помощью устройства, блок-схема которого приведена на фиг.3, которое состоит из М демодуляторов 1 сигналов локации, М блоков 2 вычисления расстояния между МС и каждой БС, М блоков 3 оценки отношения сигнал-шум, М блоков 4 оценок вероятностей наличия аномальных ошибок и блока 5 формирования оценок координат. Демодуляторы 1 сигналов локации располагаются на МС. Блоки 3 оценки отношения сигнал-шум и блоки 4 оценки вероятности наличия аномальных ошибок также находятся в составе МС.
М демодуляторов принимают сигналы локации, каждый от соответствующей БС. С первых выходов демодуляторов 1 на входы блоков 2 вычисления расстояния поступают значения временных интервалов между моментами передачи и приема соответствующих сигналов локации. В блоках 2 вычисления расстояния по этим значениям формируется величина расстояния согласно формуле pri=c(ti-t), где t - время передачи сигнала БС, ti - время приема на МС сигнала от i-й БС.
На втором и третьем выходах каждого из демодуляторов 1 сигналов локации формируются значения оценки амплитуды и мощности шума соответственно. Эти значения поступают на первый и второй входы каждого из блоков 3 оценки отношения сигнал-шум.
Полученные в демодуляторе 1 оценки амплитуды сигнала и мощности шума поступают на вход блока 3 оценки отношения сигнал-шум, где формируется соответствующая оценка. На вход блока 4 формирования оценки вероятности наличия аномальной ошибки r поступают данные из сети о углах возвышения спутников, а также информация о застройке района, в котором находится МС. В зависимости от углов возвышения спутников и информации о застройке в блоке 4 формируется оценка вероятности наличия аномальной ошибки r. Оценка вероятности наличия аномальной ошибки r может быть сформирована, например, следующим образом:
,
где α ci - угол возвышения i-го спутника, принимающего участие в локации, Нc - средняя высота зданий в районе предполагаемого нахождения МС, Lc - среднее расстояние между зданиями в районе предполагаемого нахождения МС. На фиг.5 приведен рисунок, который качественно иллюстрирует связь оценки вероятности наличия аномальной ошибки r, характеристик застройки района и угла возвышения спутника.
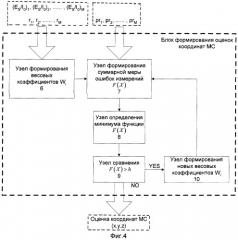
Вариант выполнения блока 5 формирования оценок координат представлен на фиг.4.
Блок 5 формирования оценок координат содержит узел 6 формирования весовых коэффициентов Wi, узел 7 формирования суммарной меры ошибок измерения F{X), узел 8 определения минимума сформированной функции F{X), узел 9 сравнения сформированной функции с порогом и узел 10 формирования новых весовых коэффициентов Wi.
Блок 5 формирования оценок координат работает следующим образом.
На вход узла 6 формирования коэффициентов поступает информация о канале распространения, а именно отношение сигнал-шум и оценка вероятности наличия аномальной ошибки для каждой БС.
Весовые коэффициенты Wi устанавливаются исходя из точности измерения псевдорасстояния для каждого спутника. Чем выше точность измерения псевдорасстояния, тем с большим весом данное измерение входит в суммарную меру ошибок измерения.
Весовые коэффициенты Wi могут быть сформированы, например,
следующим способом:
Wi=bi· ci,
где bi=1 для сигналов локации, принятых при достаточно высоком отношении сигнал-шум, обеспечивающем хорошую точность измерения;
bi<1 для сигналов локации, принятых при низком отношении сигнал-шум;
сi=1, для сигналов локации, у которых значение оценки вероятности наличия аномальной ошибки ниже порога;
сi<1, для сигналов локации, у которых значение оценки вероятности наличия аномальной ошибки выше или равно порогу. Этот порог выбирается на основе результатов полевых испытаний алгоритма локации.
Не исключаются и другие способы формирования весовых коэффициентов, которые позволят повысить точность оценки координат.
Весовые коэффициенты с выхода узла 6 формирования весовых коэффициентов и измеренные расстояния с входа блока 5 формирования оценок координат МС поступают на вход узла 7 формирования суммарной меры ошибок измерения. В нем для каждого спутника формируется мера ошибки (см. формулу (10)) между расстоянием до спутника, равным сумме псевдорасстояния и предполагаемого рассогласования часов τ , умноженного на скорость света, и фактическим расстоянием между спутником и предполагаемыми координатами МС {x,y,z}:
Суммарная мера ошибок измерения формируется согласно формуле (11). Сформированная суммарная мера ошибок измерения поступает с выхода узла 7 формирования суммарной меры ошибок измерения на вход узла 8 определения минимума суммарной меры ошибок измерения. В нем за оценку местоположения МС принимается такая точка , в которой функция (11) достигает своего абсолютного минимума.
Минимум функции (11) может быть найден известными математическими методами, например градиентным методом, описанным в [5]. Оценка местоположения МС и значение суммарной меры ошибок измерения в точке этой оценки поступают с выхода узла 8 определения минимума на вход узла 9 сравнения, где сравниваются значения суммарной меры ошибок измерения с порогом.
Для обнаружения наличия аномальных ошибок значение функции F{x,y,z,τ ) (11) в точке сравнивается с порогом hFA. Порог hFA может быть найден из трансцендентного выражения (14).
В узле 9 сравнения значение функции в найденной точке минимума сравнивается с порогом. Если значение функции в найденной точке минимума не превышает порог hFA, то считается, что ошибка в оценке местоположения МС обусловлена только наличием гауссовских ошибок, и координаты берутся за окончательную оценку местоположения и передаются на выход блока формирования оценок координат МС 5. В противном случае суммарная мера ошибок измерения передается с выхода узла 9 сравнения на вход узла 10 формирования новых весовых коэффициентов. Считается, что в измерениях псевдорасстояний содержатся аномальные ошибки, которые могут привести к большим ошибкам в оценке местоположения и необходимо определить в каких из измерений псевдорасстояний содержатся аномальные ошибки и при возможности уменьшить влияние данных ошибок на окончательную оценку местоположения. В узле 10 формирования новых весовых коэффициентов по суммарной мере ошибок измерения определяются значения взвешенных квадратов ошибок для каждого спутника согласно формуле (15) и сравниваются с порогом (16).
Если значения взвешенного квадрата ошибки (15) для данного спутника превышает порог (16), то значение весового коэффициента, соответствующего данному спутнику, изменяется согласно выражению (17).
Затем полученные новые весовые коэффициенты с выхода узла формирования новых весовых коэффициентов передаются на вход узла формирования суммарной меры ошибок измерения, в котором ищется новая оценка местоположения, т.е. минимум функции (11), с использованием новых весовых коэффициентов (17).
Таким образом, в предлагаемом способе в отличие от уже известных способов предлагается не удалять измерения спутников, содержащих аномальные ошибки, а уменьшать вес этих ошибочных измерений, и затем искать заново местоположение абонентской МС с использованием скорректированных весовых коэффициентов. Данная операция выполняется до тех пор, пока сумма взвешенных мер ошибок, соответствующих скорректированному местоположению абонентской МС, с использованием уточненных весовых коэффициентов не станет меньше порога. Полученная таким образом скорректированная оценка местоположения абонентской МС принимается за окончательную оценку местоположения абонентской МС.
Таким образом, полученное решение является адаптивным способом оценки точности измерений и изменения весов этих измерений на основе полученных оценок. Предложенная методика позволяет определить долю участия каждого измерения в окончательном решении. Такой способ оценки, в отличие от большинства известных методов, которые направлены на исключение измерений с большими ошибками из рассмотрения, позволяет использовать все имеющиеся измерения. Это обеспечивает более высокое качество оценки в условиях, когда нет возможности выделить достаточное для решения навигационной задачи число измерений с малыми ошибками.
1. Способ определения местоположения абонентской мобильной станции (МС), заключающийся в том, что принимают N сигналов локации, соответствующих каждой из N базовых станций (БС), по принятым сигналам локации оценивают псевдорасстояния от МС до каждой из N БС, для каждой БС определяют меру ошибки по оцененному псевдорасстоянию до абонентской МС, для каждой БС определяют весовой коэффициент меры ошибки, суммируют взвешенные меры ошибки и сравнивают их с порогом, за начальное местоположение абонентской МС принимают то, для которого сумма взвешенных мер ошибок минимальна, отличающийся тем, что если сумма взвешенных мер ошибок, соответствующих начальному местоположению абонентской МС, больше порога, то уточняют весовые коэффициенты мер ошибок таким образом, что для БС, у которых взвешенная мера ошибки, соответствующая начальному местоположению абонентской МС, меньше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок оставляют без изменения, для БС, у которых взвешенная мера ошибки, соответствующая начальному местоположению абонентской МС, больше средней взвешенной меры ошибки по всем БС, весовые коэффициенты мер ошибок уменьшают, корректируют местоположение МС с использованием уточненных весовых коэффициентов, определяют