Способ определения громкости тонов для произвольной частоты звуков по е.л.овчинникову с учетом закона вебера-фехнера
Иллюстрации
Показать всеИзобретение относится к медицинской технике и практике, в частности к оториноларингологии, а именно к аудиометрическим методам исследования слуха. Способ включает обоснование и расчет громкости акустического сигнала произвольной частоты по известной его интенсивности (звуковому давлению). Установлена зависимость отношения энергий равногромких - исследуемого и стандартного - звуков, имеющая смысл коэффициента преобразования их энергии по частоте. Представлен вывод закона Вебера-Фехнера по Е.Л.Овчинникову для произвольной частоты звуковых волн. 2 з.п. ф-лы, 16 ил.
Реферат
Изобретение относится к медицинской технике и практике, в частности к оториноларингологии, конкретно к аудиометрическим методам исследования слуха.
Известно, что стандартное ухо человека способно воспринимать звуки в очень большом диапазоне частот: Δ f = 20 Гц - 20 кГц, что соответствует ее изменению на три порядка [1].
Еще более обширен диапазон звуковой энергии (интенсивности, или силы звука, и звукового давления) [2]. Физиологические значения этих величин (не приводящие к деструктивным изменениям органа слуха) по абсолютному значению составляют интервалы:
- для интенсивности I: от минимального значения Io=10-12 до максимального
- для звукового давления Δ р: от минимального значения Δ ро=2· 10-5 до максимального Δ pmo=63 Па=2· 101,5 Па.
Существует особая единица измерения величин, изменяющихся в больших пределах, - единица логарифмической относительной величины (десятичного логарифма отношения двух однородных величин) [3]. Единица измерения некоторой произвольной величины X, определяемая по отношению к Хо, принимаемой за некоторую предельную, как
(1)
называется белом: [L]=1 Б.
Величина, в 10 раз меньшая бела, называется децибелом: 0,1 Б=1 дБ.
Шкала интенсивности звука (звукового давления) в белах устанавливается как отношение интенсивности данного звука I (звукового давления Δ р) к минимальному, пороговому, (Δ po=2· 10-5 Па соответственно):
Интенсивность I по определению [4] устанавливается соотношением
где W - полная механическая (кинетическая колебательного движения Wk и потенциальная взаимодействия Wp частиц среды) энергия звуковой волны.
Интенсивность I и звуковое давление Δ P акустических волн связаны между собой соотношением
причем эффективное (измеряемое на практике и воспринимаемое ухом) звуковое давление
где Δ ра - его амплитудное значение, ρ v=z - волновое (акустическое) сопротивление среды.
Тогда единица логарифмической относительной интенсивности
Наличие пороговых (максимальных) значений интенсивности звука Imo = 10 Вт/м2 и звукового давления Δ рmo=63 Па=2· 101,5 Па, превышение которых приводит к дискомфортным слуховым эффектам и даже к деструктивным изменениям структур органа слуха, дает возможность определить соотношение между верхним и нижним значениями относительных интенсивностей звука (звуковых давлений). Оно составляет
и
или
Это позволяет разделить весь воспринимаемый ухом диапазон интенсивностей звука (звуковых давлений) на 13 единиц такой равномерной (линейной) шкалы, каждая из которых соответствует отношению интенсивностей двух звуков, равному 10 (отношению двух звуковых давлений, равному ). Тогда 1 бел интенсивности звука (звукового давления) - это единица равномерной (линейной) шкалы уровней интенсивности звука (звукового давления), соответствующая изменению интенсивности в 10 раз (изменению звукового давления в раз).
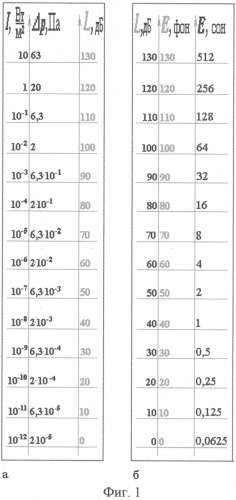
На фиг.1а представлено соответствие между шкалами интенсивности звука I в ваттах на квадратный метр, звукового давления Δ р в паскалях, и уровней интенсивностей (уровней звукового давления) L в децибелах.
Экспериментально выявлено (E.H.Weber, 1834) [5, цит. по: 6], что существует наличие закономерных соотношений между силой воздействия внешних физических раздражителей и вызываемыми ею субъективными реакциями рецепторных систем - ощущениями. E.H.Weber установил так называемый психофизический закон: за счет адаптации рецепторных систем воспринимается не абсолютный АХ, а относительный прирост раздражителя величины X, причем
Математическое обоснование (G.Th.Fechner, 1858) этого закона (6) привело к закону Вебера - Фехнера [7, цит. по: 8], по которому интенсивность ощущения S выражается соотношением
S=klnX+c, (7)
где k и с постоянные.
В биологической акустике закон Вебера - Фехнера для слуха устанавливает связь силы раздражителя - интенсивности звука I (или звукового давления Δ р) - с вызываемым ею субъективным ощущением - громкостью звука Е.
По Веберу, для слуха восприятие приращения громкости Δ Е прямо пропорционально относительному приращению интенсивности звука
По Фехнеру, переход от конечных разностей к бесконечно малым дает дифференциальное уравнение
интегрирование которого в неопределенных пределах
приводит к общему решению
E=klnI+c. (10)
Константа интегрирования с определяется использованием начального условия, по которому минимальная пороговая интенсивность звука вызывает, по определению, ощущение громкости Еo=0.
Оно устанавливает, что с=klnIo, так что
Далее декларативно принимается условие, что коэффициент k в решении (11) выбирается таким, что при стандартной частоте fc=1 кГц при переходе от натурального логарифма к десятичному он становится равным 1. Такой способ представления закона Вебера - Фехнера излагается во всех учебниках, руководствах и пособиях, научной литературе. В итоге закон Вебера - Фехнера предстает в виде
Закон Вебера - Фехнера для стандартной частоты fc=1 кГц в форме (12) устанавливает единицу громкости слухового ощущения. При этой частоте 1 дБ по шкале интенсивности принято считать равным 1 дБ по шкале громкости:
1 дБгромкости=1 дБинтенсивности.
1 дБ громкости характеризует уровень слухового ощущения и называется фоном:
1 дБгромкости=1 фон,
Тогда громкость звука произвольной интенсивности в фонах определяется как
На практике используется также шкала громкости с единицей измерения сон [9]: "1 сон равен громкости тона в 1000 Гц при уровне звукового давления 40 дБ". Установлена связь между единицами громкости тонов в сонах и белах (децибелах).
На фиг.1б представлено соответствие между шкалами уровней интенсивностей звука (уровней звукового давления) L в децибелах, уровней громкости Е в фонах и уровней громкости Е в сонах.
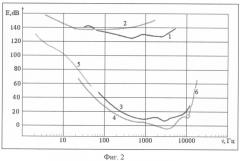
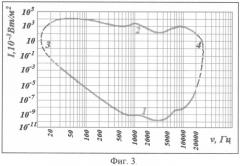
Для остальных частот звукового диапазона закон Вебера - Фехнера установлен только экспериментально ([10-15, 17], фиг.2: аудиограмма 1 - по R.L.Wegel, 1932; аудиограмма 2 - по G.Bekesy, 1936; аудиограмма 3 - по R.S.Dadson, J.A.King, 1952; аудиограмма 4 - по D.W.Robinson, R.S.Dadson, 1965; аудиограмма 5 - по N.S.Yeowart, M.Bryan, W.Tempest, 1967; аудиограмма 6 - по J.L.Northern, M.P.Downs, R.S.Dadson, A.Glorig, J.Fletcher, 1972; рисунок выполнен по [16] с изменениями). Аудиограммы пороговых значений громкости звуковых волн оригинально представлены на фиг.3 [17, с изменениями]: аудиограмма 1 соответствует порогу слышимости, аудиограмма 2 - болевому порогу. Пунктирными кривыми 3 и 4 показано вероятное соединение обеих кривых для тех частот, для которых аудиометрический эксперимент затруднителен. Этими кривыми ограничена вся область слышимости для человеческого уха.
Аудиометрические исследования слуха свидетельствуют: понижение частоты звука f в звуковом диапазоне от стандартной fc=1 кГц до минимально воспринимаемой fo=20 Гц и повышение ее от стандартной до максимально воспринимаемой fmo=20 кГц (фиг.2) для равногромких звуков на любом уровне громкости n требует для увеличения интенсивности тестируемого звука Inf относительно стандартной Inс. Эти эксперименты противоречат закону Вебера - Фехнера, которым утверждается обратное, а именно, - равенство интенсивностей равногромких звуков Inf=Inc, поскольку Enf=Enc и . Экспериментально наблюдается и противоположный эффект, по которому звуки равных интенсивностей производят ощущение разных громкостей, хотя по закону Вебера - Фехнера это не может быть исполнимо. Эти парадоксы восприятия звука в литературе не описаны, хотя аудиограммы свидетельствуют об их наличии.
Способа расчета громкости звуков произвольных частот и интенсивностей (звукового давления) не представлено. Отмечается только экспериментальный способ определения громкости звука сравнением его интенсивности с интенсивностью звука стандартной частоты, приводящей на слух к ощущению той же громкости [4] и оцениваемой уровнем громкости звука стандартной частоты. Звуки разных частот, соответствующие одному уровню громкости, называются (считаются) равногромкими. На практике используют анализаторы шума (например, АШ-2М) и измерители интенсивности шума и вибрации (ИШВ-1) [Каспаров А.А. Гигиена труда и промышленная санитария. - М.: Медицина, 1981. - С.143-150]. Они позволяют оценить общий уровень шума и уровень звука на конкретных фиксированных частотах.
Целью данного изобретения является построение способа определения громкости звука произвольной частоты и интенсивности (звукового давления).
Сущность изобретения заключается в том, что на основе закона Вебера - Фехнера для стандартной частоты fc=1 кГц и биофизической (волновой) модели слуха, механизма восприятия высоты и равногромкости тонов, включая использование аудиометрического метода исследования спектральных характеристик уха на фиксированных частотах, устанавливается закон Вебера - Фехнера для произвольной частоты и интенсивности звука в общем виде
или в виде
Enf=Enc+(Еmо-Еnc) OE(f),
где - искомая громкость исследуемого сигнала произвольной частоты f и интенсивностью Inf, в декафонах, при минимальной пороговой интенсивности на стандартной частоте fc=1 кГц, декафон - максимальная комфортно воспринимаемая на слух громкость звукового сигнала стандартной частоты интенсивностью , - громкость звукового сигнала стандартной частоты, равногромкого тестируемому интенсивностью Inf; - громкость звукового сигнала исследуемой частоты интенсивностью Iof, равногромкого пороговому на стандартной частоте, OE(f) - частотная функция, равная
для которой v
| * |
| с |
| * |
| f |
Технический результат изобретения состоит в достоверном определении искомого уровня громкости тонов для звуков произвольной частоты и интенсивности.
В законе Вебера - Фехнера переход от натурального логарифма к десятичному в (11) происходит как .
Для граничного (второго предельного) условия дифференциального уравнения (9), его общего (10) и частного (11) решений, для которых максимальная пороговая интенсивность звука Imo=10 вызывает громкость, по определению равную Еmо, имеем Еmо=, откуда и
Но поскольку по определению , или , то устанавливается привычная форма записи закона Вебера - Фехнера для слуха (12)
справедливая, однако, только для стандартной частоты fc=1 кГц.
Именно этим законом определяется единица измерения громкости звука - фон. Громкость в сонах устанавливает закон Стивенса [9]. По этому закону в отличие от логарифмического Вебера - Фехнера, утверждается, что ощущение громкости звука носит степенной характер и нарастает пропорционально интенсивности звукового стимула:
Ecoн=kIn. (14)
Имея определенную величину в 1 сон при эталонном тоне в 1000 мел (звуке стандартной частоты 1 кГц), громкость звука в Е сонов определяется при интенсивности, в Е раз превышающей его первоначальную. Для эталонного тона 1000 мел между громкостью звука в фонах и сонах установлено соотношение (фиг.5):
1 сон=40 фонов=4 декафона (дафон).
Связь между громкостью в фонах и сонах можно установить не только графически, но аналитически. При этом оказывается, что оба закона: и Вебера - Фехнера, и Стивенса, - являются тождественными. Автору не удалось отыскать в доступной ему литературе установления этого заключения, и он приводит собственное математическое обоснование.
Уравнение соответствия между законами Вебера - Фехнера и Стивенса, определяемое прямой (фиг.5), можно записать в виде
log2Ecoн=Едафон-4=LБ-4=,
откуда получается закон Стивенса
выраженный действительно в виде степени (14), где показатель степени
n=lg2=0,3010,
а коэффициент , при этом
и
I
| lg2 |
| o |
Таким образом, утверждение, что закон Стивенса является альтернативным [23], не вполне корректно - это просто иная запись одного и того же эффекта. Однако значение закона Стивенса велико потому, что он позволяет пользоваться не относительными параметрами интенсивности звука, а их абсолютными значениями.
Но, с другой стороны, закон Вебера - Фехнера устанавливает линейное определение относительной интенсивности звука, а закон Стивенса определяет эту интенсивность звука в виде степени.
На фиг.6 представлены результаты собственных расчетов по установлению тождественности законов Вебера - Фехнера и Стивенса. Заданы константы n=lg2 и Io=10-12 Вт/м2, интервал изменения возможных значений реальной интенсивности звука: N∈ [-12, 1], так что I(N)∈ [10-12, 10], представлены законы (12) и (14). Приведено графическое представление Ефон(I) и Есон(I). Нижний график точно соответствует закону Стивенса, а верхний показывает его степенной характер (14).
Акустоволновая модель слуха [19], построенная на результатах классических экспериментов [11, 24], устанавливает механизм звукопроведения на первом этапе дорецепторного звена слухового органа и описывает образование стоячей волны на преддверной мембране улиткового протока, трансформируя распространение энергии волны стимула в направлении сенсорных клеток (перпендикулярно длиннику улиткового протока).
Теория механизма стимуляции сенсорных (волосковых: и внутренних, и наружных) клеток слухового анализатора трактуется еще довольно противоречиво [25, 26]. Но то, что генерация ими электрического потенциала связана с колебаниями покровной мембраны относительно ВК на базилярной пластинке, бесспорно. Выбор же возбуждаемого рецептора устанавливается распределением того звукового поля, которое формируется стоячей волной на преддверной мембране [19].
Итак, первый этап преобразования акустической энергии волны в электрический потенциал во внутреннем ухе представлен (качественно и количественно) акустоволновой моделью слуха [19]. После создания в вестибулярной лестнице продольных звуковых волн частотой f колебательным движением основания стремени в окне преддверия происходят эффекты, приводящие к дисперсии волн с параметром
так что скорость волн с учетом (15)
v(f)=vmo(1+22lg(f/fmo))/2. (16)
После отражения волн на апексе улиткового протока в вестибулярной лестнице и на преддверной мембране наблюдается интерференция прямых и отраженных волн. Ее результатом является образование на преддверной мембране поперечных стоячих волн. Их максимумы (пространственные хmах(f) и lmax(f) и временные tmax(f)) целиком определены частотой звукового сигнала, поступающего в ухо. Для мембраны стандартной длины Lo они представлены соотношениями [19]
Xmax(f)=Lo(1-δ (f)), (17)
lmax(f)=Loδ(f), (18)
tmax(f)=Lo(1+δ (f)/v(f)+n/f, (19)
где х - продольные координаты максимумов стоячих волн на преддверной мембране, отсчитываемые от базального участка улиткового протока; δ =(Lo-x)/Lo=22lg(f/fmo) - безразмерные (относительные), l=Lo-x=Loδ- продольные координаты тех же максимумов на преддверной мембране, отсчитываемые от апекса улиткового протока, n=0, 1, 2, ... - целое число, имеющее смысл номера временного максимума стоячей волны частотой f.
Второй этап преобразования акустической энергии волн в электрический потенциал во внутреннем ухе феноменологически может быть представлен следующим образом. Он начинается преобразованием механической энергии стоячих волн - колебаний преддверной мембраны (в координате xmax(f) или lmax(f)) - в волновой процесс. Рожденная волна той же частоты, распространяясь в эндолимфатическом протоке перпендикулярно текториальной мембране, вызывает ее колебания и воздействие на сенсорные клетки, провоцируя в них появление электрического (генераторного) потенциала.
Автором было показано [22], что за восприятие частоты звуков (измеряемой в герцах) как высоты тонов (определяемой в мелах) ответственны сенсорные (волосковые) клетки внутреннего ряда спирального органа - ВВК. Распределение на базилярной пластинке ВВК, имеющих порядковый номер N при отсчете от апекса улиткового протока и воспринимающих частоту f(N) как тон высотой P(N), удовлетворяет соотношению [21]
в то время как частота, ответственная за ощущение тона высотой P(N)
устанавливается соотношением
Тогда расстояния между ВВК могут быть рассчитаны по очевидному соотношению
λ (N)=lВВК(N+1)-lВВК(N). (23)
Теперь обоснуем предложение, что громкость звука определяется числом n вовлеченных в процесс восприятия акустической энергии сенсорных (волосковых) клеток наружных рядов спирального органа - НВК, которые по координатам соотнесены с волосковыми клетками внутреннего ряда, отвечающими за восприятие частоты. При этом номер n-ого уровня громкости может быть отождествлен с указанным числом n НВК, участвующих в преобразовании акустической энергии в рецепторный потенциал.
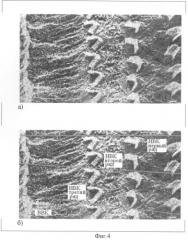
Количество НВК на базилярной пластинке, расположенных в три ряда, превышает число ВВК примерно в шесть раз [27]. Простой расчет показывает, что плотность распределения НВК на базилярной пластинке вдвое больше, чем ВВК (микрофотография [28], фиг.4а; ее анализ, подтверждающий вывод о более плотном распределения НВК по сравнению с ВВК - на фиг.4б).
При этом расстояния между НВК также являются функцией частоты Λ (f) или тона Λ (N).
Громкость звука - субъективная характеристика слуха в том смысле, что она интимно (индивидуально) воспринимается рецепторами спирального органа, для которых и предназначен закон Вебера - Фехнера (8).
Два звука, произвольной и стандартной частот, будут равногромкими (иметь равные уровни громкости E
| * |
| nf |
| * |
| nc |
| * |
| nf |
| * |
| nc |
наблюдаемого в рецепторном отделе уха. Равенство отражает ответ сенсоров на их раздражение, проявляясь в субъективности слуховых ощущений. Но, по Веберу, оно является объективным для количественных соотношений при преобразовании энергии в рецепторном отделе.
Тогда во внутреннем ухе для равногромких сигналов с интенсивностями I
| * |
| nf |
| * |
| nc |
| * |
| nf |
| * |
| nc |
I
| * |
| nf |
| * |
| nc |
или
так что, используя (2),
В этом уравнении S
| * |
| f |
| * |
| c |
| * |
| с |
| * |
| f |
где v
| * |
| f |
| * |
| c |
Привлекая два последних соотношения к равенству (24), имеем
Здесь частотный коэффициент равногромкости тонов G(f) - величина, определяющая отношение энергий равногромких - исследуемого и стандартного, - звуков, имеет смысл коэффициента преобразования их энергии по частоте и не зависит от номера уровня.
На практике интенсивность звука определяется измерением ее величины в наружном слуховом проходе. Поступающая в наружный слуховой проход энергия звуковых волн Wnf произвольной частоты f, отнесенная к предельно воспринимаемой Woc, (мы будем рассматривать, как принято в акустике, относительное значение энергии относительно пороговой Woc) равна относительной интенсивности этих волн. Для равногромких звуков n-ого уровня будет выполнимо условие
так как звуковая энергия приходится на одну и ту же барабанную перепонку и длительности времени прохождения волнами расстояния от входного отверстия наружного слухового прохода до барабанной перепонки можно считать равными из-за малости эффекта дисперсии в воздухе.
Преобразование энергии происходит в соответствии с законом сохранения и превращения энергии. Он, в виде
приводит к равенству
Закон Вебера - Фехнера (12) для произвольного n-ого уровня громкости звука частотой f предстанет в виде
так как на стандартной частоте и - громкость звука стандартной частоты fc, равногромкого звуку частоты f. Поэтому
С другой стороны, привлекая (27), получаем
Enf-Enc=kln G(f).
Для частот f→ fo и f→ fmo, для которых Inf→Imo, имеем Enf→Еmо и G(f)→ Gmo. Тогда
Emo-Enc=kln Gmo,
откуда
Это приводит к соотношению
,
где частотная функция
OE(f)=lgG(f)lge, (29)
как и частотный коэффициент G(f), имеет смысл отношения энергий равногромких звуков разных частот и также не зависит от номера уровня.
Аудиограммы и расчеты показывают, что для любой частоты OE(f)>OE(fc), причем OE(fmo)=lg G(fmo) lge=1.
Поскольку на любом уровне G(t)>G(fc), то Wnf|f<fc>W
| * |
| nc |
Исходя из этих представлений, закон Вебера - Фехнера для n-ого уровня громкости звука произвольной частоты f можно представить в виде
Enf=(Emo-Enc)OE(f)+Enc. (30)
Для нулевого уровня
Eof=EmoOE(f), (31)
откуда находим зависимость используя которую, получаем новую форму записи закона Вебера - Фехнера в авторской форме
Упрощение (32) приводит к изящной записи закона Вебера - Фехнера в авторской форме
Иллюстрацией выводов автора подтверждается созданной им компьютерных программ "Loudness_W-F" разных серий и назначений в расчетной среде Math-CAD [29]. Программа "Loudness_W-F_01" (фиг.7а, б, в, г) дает общее представление о параметрах структур внутреннего уха и их соотношениях между собой и расчет громкости звука по формуле (30). На фиг.8 приведена только итоговая, четвертая, страница исполнения программы "Loudness_W-F_02" с расчетом громкости звука по формуле (32).
С учетом связи (22) частоты звукового сигнала с высотой тона, ощущаемого на слух человеком, формулы (30) и (32) приобретут вид
EnN=(Emo-Enc)OE(N)+Enc. (34)
На фиг.9 представлена также только итоговая, четвертая, страница программы "Loudness_W-F_03" с расчетом громкости тонов по формуле (34), а на фиг.10 страница программы "Loudness_W-F_04" с расчетом громкости тонов по формуле (35).
На фиг.11-13 приведены результаты расчета громкости звука для тонов по формуле (34) в пространственной системе координат EnN в трех разных проекциях.
Для граничных (очень низких и очень высоких) частот звукового диапазона выполнение закона Вебера - Фехнера в авторской форме нарушается в связи с допущением условия постоянства просвета эндолимфатического протока (24), поскольку до сих пор еще не определены морфологические параметры этого просвета в местах крепления мембран к улитке как костному образованию и вблизи апикальной связки мембран [30]. Кроме того, здесь не учитывается также влияние интенсивности звука в области максимальной чувствительности уха [31], приводящей к повышению уровня громкости для частот Δ f~3,5-4 кГц.
Для того чтобы, зная интенсивность (звуковое давление) тестируемого акустического сигнала заданной частоты fт, установить громкость, которую он будет оказывать на наш орган слуха - уши, надо задать величину его интенсивности Iт (звукового давления Δ рт) или измерить ее виброметром (или измерительным микрофоном) [32], вычислить или по установочному графику (фиг.14) определить частотный коэффициент преобразования акустической энергии OE(fт) и рассчитать громкость n сигнала по компактной формуле, вытекающей из (30), в форме
где - минимально воспринимаемая на слух интенсивность звукового сигнала, , Enc=nт, декафон - максимальная комфортно воспринимаемая на слух громкость звукового сигнала. Считая значения OE(f) известными для любой частоты, искомый уровень громкости для установленной интенсивности звукового сигнала I определяется соотношением
а при установленном звуковом давлении тестируемого сигнала Δ рт - с использованием соотношения (6)
где Δ ро=2· 10-5 Па, - минимальное пороговые значение комфортно воспринимаемых ухом звукового давления, Δ рmо=6,5 декафон - максимальный комфортно ощущаемый на слух уровень звукового давления.
При известной связи (22) частоты звукового сигнала с высотой тона, ощущаемого на слух человеком, формулы (33) и (34) приобретут вид
где OE(Nт) - тоновый коэффициент преобразования энергии равногромких тонов в диапазоне Δ Р=0-3250 мел (его величину для тестируемого сигнала можно определить также по установочному графику, фиг.15). При этом изменится вид изофон - кривых равных громкостей, но их тенденция и суть процессов, естественно, останутся прежними. Примеры расчетов громкости тонов с выводом результатов для различных высот (частот звуков) приведены на фиг.16.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Голямина И.П. Звук//Физика. БЭС. - Бол. Рос. Энцикл. - 1999. - С.198.
2. Звуковое давление//Физика. БЭС. - Бол. Рос. Энцикл. - 1999. - С.198-199.
3. Бел//Физика. БЭС. - Бол. Рос. Энцикл. - 1999. - С.49.
4. Яворский Б.М., Детлаф А.А. Справочник по физике. - М.: Наука. - 1964.
5. Weber E.H. Die Pulsu, Resorbtion, Auditu und Tactu. - Lipsiae. - 1834.
6. Ярошевский М.Г. Вебер Х.Ф.//БСЭ. - Т.4. - 1971. - С.348-349.
7. Fechner G.Th. Elemente der Psychophysic. - Lpz. - 1860.
8. Ярошевский М.Г. Фехнер Г.Т.//БСЭ. - Т.27. - 1977. - С.326-326.
9. Stevens S.S. A scale for the meassurement of a psychological magnitude: Loudness. - Psych. Rev. - 1936. - V.43. - P.405-416.
10. Wegel R.L. Physical data and physiology of excitation of the auditory nerve.//Ann. Otol. - 1932. - v.41. - pp.740-779.
11. G. Experiments in Hearing. - N.Y. McGraw-Hill. - 1960.
12. Dadson R.S., King J.A. A determination of the normal threshold of hearing and its relation to the standardization of audiometers.//J. Laring. Otol. - 1978. - V.46. - Р.368-378.
13. Robinson D.W., Dadson R.S. A re-determination of the equal loudness relations for pure tones.//Brit. J. Appl. Phys. - 1956. - V.7. - P.166-181.
14. Yeowart N.S., Bryan M., Tempest W. The monaural MAP threshold of hearing at frequencies from 1.5 to 100 c/s.//J. Sound. Vib. - 1967. - V.6. - P.335-342.
15. Northern J.L., Downs M.P., Dadson R.S., Glorig A., Fletcher J. Recommended high-frequency audiometric threshold levels (8000-18000 Hz).//J. Acoust. Soc. Amer. - 1972. - V.5. - P.585-595.
16. Гельфанд С.А. Слух: введение в психологическую и физиологическую акустику./Пер. с англ. - M.: Медицина. - 1984.
17. Цедрик М.С., Бирич Е.В., Макеева Г.П., Савицкая И.Ф. Физика в графиках. - Минск: Высшая школа. - 1964.
18. Руководство по оториноларингологии./Под ред. И.Б.Солдатова. - M.: Медицина. - 1997.
19. Овчинников Е.Л., Еремина Н.В. Способ выявления биофизических процессов, реализующих механизм и биофизическую (волновую) модель слуха человека. Патент РФ №2146878//Бюлл. изобр. - 2000. - №9 (II).
20. Овчинников Е.Л., Еремина Н.В., Голенищев В.Ю. Способ неинвазивного определения длины базилярной пластинки внутреннего уха человека. Патент РФ №2160038//Бюлл. изобр. - 2000. - №34.
21. Овчинников Е.Л., Еремина Н.В., Хохлова Н.Ю. Способ установления координатного распределения внутренних волосковых клеток на базилярной пластинке периферического отдела слухового анализатора человека. Патент РФ №2184485//Бюлл. изобр. - 2002. - №19.
22. Овчинников Е.Л. Способ установления единицы высоты тона (мел) и определение его физического смысла. Патент РФ №2196508//Бюлл. изобр. - 2003. - №2.
23. Пузырей А.А. Стивене С.С.//БСЭ. - М.: Советская Энциклопедия - Т.24. - Кн.1. - С.511.
24. Schuknecht H.F. Pathology of the Ear. A Commonwealth Fund Book./Harward Univ. Press. - Cambridgem Massachusets. - 1974.
25. Ryan A., Dallos P. Physiology of the inner ear./Hearing Disorders//Ed. J.L.Northem, Boston: Little Brown. - 1976. - P.89-101.
26. Ходжкин А. Нервный импульс. - М.: Мир. - 1965.
27. Гистология/Под ред. В.Г.Елисеева, Ю.И.Афанасьева, Н.А.Юриной. - М.: Медицина. - 1983.
28. Lin D.J. Fine morphology of the tectorial memdranes: Itsrelationship tothe organ of Corti. Arch. Otol. - 1972. - N96. P.199-215.
29. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. - М.: СК Пресс. - 1997.
30. Овчинников Е.Л. Способ установления эффекта возрастной эволюции улиткового протока внутреннего уха человека и определение биофизических параметров его временных изменений. Патент РФ №2169523//Бюлл. изобр. - 2001. - №18.
31. Овчинников Е.Л., Еремин С.А., Еремина Н.В. и др. Способ определения и расчета линейных параметров наружного слухового прохода уха человека. Патент РФ №2194434//Бюлл. изобр. - 2001. - №35.
32. Колесников А.Е. Ультразвуковые измерения. М.: Изд. стандартов. - 1970.
1. Способ определения громкости тонов для произвольной частоты звуков с учетом закона Вебера-Фехнера, включая использование аудиометрического метода исследования спектральных характеристик уха на фиксированных частотах, отличающийся тем, что на основе биофизической волновой модели слуха, механизма восприятия высоты и равногромкости тонов устанавливают закон Вебера-Фехнера для произвольной частоты и интенсивности в общем виде
или в виде
Enf=Enc+(Emo-Eno)OE(f),
где - искомая громкость исследуемого сигнала произвольной частоты f и интенсивностью Inf, в декафонах, при минимальной пороговой интенсивности на стандартной частоте fc=1 кГц,
декафон - максимальная комфортно воспринимаемая на слух громкость звукового сигнала стандартной частоты интенсивностью
- громкость звукового сигнала стандартной частоты, равногромкого тестируемому интенсивностью Inf,
- громкость звукового сигнала исследуемой частоты интенсивностью Iof, равногромкого пороговому на стандартной частоте,
OE(f) - частотная функция, для тестируемой частоты fт равная
для которой и - скорости звуковых волн стандартной и тестируемой частот, диспергированных в пери- и эндолимфатическом протоках,
Λс и Λfт - расстояния между наружными волосковыми клетками, воспринимающими энергию звуков этих частот,
после чего искомый уровень громкости nт тестируемого сигнала частотой fт и интенсивности Iт определяют по формуле
2. Способ по п.1, отличающийся тем, что для тестируемого сигнала частотой fт инструментально измеряют звуковое давление Δрт, устанавливают значение частотной функции ОЕ(fт) и определяют искомый уровень громкости nт по формуле
где Δро=2·10-5 Па - минимальное пороговое значение воспринимаемых ухом звукового давления,
- максимальный уровень звуков