Способ формирования многолепестковых диаграмм направленности антенной решётки

Способ формирования многолепестковых диаграмм направленности антенной решётки

Иллюстрации

Показать все

Реферат

Изобретение относится к антенной технике и может быть использовано для формирования многолепестковых диаграмм направленности (ДН) в антенных решетках (АР) с амплитудно-фазовым (комплексным) управлением.

Известен способ формирования ДН антенной решетки с максимальным коэффициентом направленного действия (КНД) [1], основанный на взвешивании сигналов, принятых каждым излучателем, и последующем их суммировании, при котором комплексные весовые коэффициенты (КВК) находят как главный вектор пучка эрмитовых форм, соответствующий наибольшему характеристическому числу пучка, причем при определении главного вектора пучка используют информацию о направлении ориентации максимума диаграммы направленности, а в качестве первой и второй эрмитовых форм пучка используют соответственно квадрат модуля ДН в направлении максимума луча и среднее значение ДН по мощности.

Существо известного способа заключается в представлении КНД (здесь рассматривается двухмерный вариант)

в виде отношения эрмитовых форм

В(1) и (2) приняты следующие обозначения:

ϕ₀ - направление ориентации максимума ДН;

|J〉 - вектор-столбец КВК с элементами J_n, где n - номер излучателя (n=1,2,...N);

[А1] и [B1] - эрмитовы матрицы порядка N с элементами

f(ϕ) - ненормированная амплитудная ДН системы, возбужденной током |J〉, которая может быть представлена в виде

Через (f) обозначена N-мерная вектор-строка ненормированных парциальных диаграмм f_n(ϕ) решетки, n-й излучатель которой возбужден током единичной амплитуды.

Поскольку матрицы [А1] и [B1] эрмитовы, то D1(J) является отношением эрмитовых форм. Входящие в (2) эрмитовы формы определяют пучок форм

который является регулярным, так как форма |J〉*[B1]·|J〉 положительно определена, что обусловлено ее физическим смыслом.

Максимум (2) равен наибольшему характеристическому числу пучка форм (6), причем этот максимум достигается только на соответствующем этому числу главном векторе пучка [2].

В соответствии с [2] максимальным собственным значением пучка эрмитовых форм (6) является максимальное собственное значение матрицы [D1], определяемой как

а собственный вектор, соответствующий максимальному собственному значению матрицы [D1] и будет решением задачи оптимизации (1). При определении главного вектора пучка используют информацию о направлении ориентации луча диаграммы направленности, а в качестве первой и второй эрмитовых форм пучка используют квадрат модуля ДН в направлении максимума луча и среднее значение ДН по мощности.

Известный способ обеспечивает максимизацию КНД решетки с произвольным расположением элементов (линейных, дуговых, кольцевых, плоских и т.д.).

Недостатком известного способа максимизации КНД является то, что он обеспечивает возможность формирования лишь однолучевых ДН. В ряде случаев на практике антенна должна обеспечивать обслуживание не одного направления, а двух-трех либо даже большего числа направлений, положение которых может изменяться. Требуемый КНД антенны в этих направлениях в общем случае может быть различным.

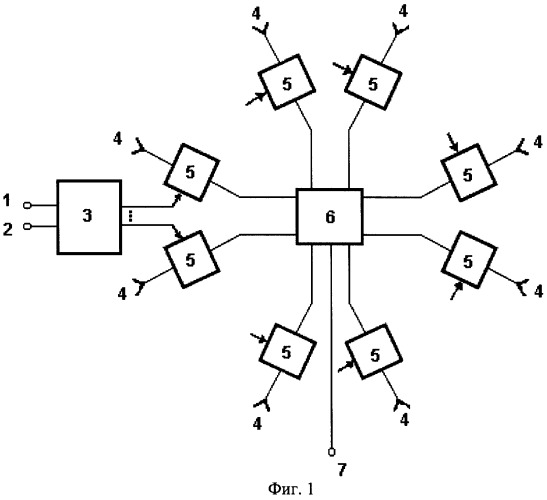
Предлагаемый способ направлен на устранение упомянутого недостатка известного способа. Структурная схема кольцевой антенной решетки, функционирующей по предлагаемому способу, представлена на фиг.1. На фиг.2 и 3 представлены сформированные на базе предлагаемого метода диаграммы направленности с различным числом лепестков и разными весовыми коэффициентами.

Рассмотрим существо предлагаемого способа. Как и в прототипе, сигналы, принятые каждым излучателем, взвешивают с помощью КВК, после чего их суммируют, причем комплексные весовые коэффициенты находят как главный вектор пучка эрмитовых форм, соответствующий наибольшему характеристическому числу пучка, а в качестве второй эрмитовой формы пучка выбирают среднее значение диаграммы направленности по мощности. Однако в отличие от прототипа при определении главного вектора пучка эрмитовых форм используют информацию о направлениях ориентации основных лепестков (“лучей”) диаграммы направленности и их относительных уровнях. При этом в качестве первой эрмитовой формы пучка выбирают квадрат модуля взвешенной суммы значений диаграммы направленности в направлениях формируемых лепестков.

Проведенный сравнительный анализ заявленного способа и прототипа показывает, что заявляемый и известный способы отличаются режимом выполнения операции взвешивания, так как при определении главного вектора пучка эрмитовых форм используют информацию о направлениях ориентации лепестков диаграммы направленности и их относительных уровнях, а в качестве первой эрмитовой формы пучка выбирают квадрат модуля взвешенной суммы значений диаграммы направленности в направлениях формируемых лепестков.

Рассмотрим предлагаемый способ формирования многолепестковых диаграмм направленности на примере N-элементной кольцевой антенной решетки радиуса R (фиг.1), в каждом канале которой имеется устройство комплексного взвешивания J_n (n=1,2,...N). Выходы всех устройств комплексного взвешивания соединены с входами сумматора, на выходе которого формируется диаграмма направленности f(ϕ).

Для формирования в диаграмме направленности в направлениях ϕ_s (s=1,2,...S) “лучей” с относительной амплитудой w_s будем искать N-мерный вектор-столбец комплексных амплитуд токов в излучателях, максимизирующий следующий энергетический функционал

где fS - взвешенная сумма значений ДН f(ϕ) в S направлениях

С учетом (5) взвешенная сумма значений ДН в S направлениях может быть представлена в следующем виде:

Здесь (fs) - N-мерная вектор-строка с элементами

При этом квадрат модуля взвешенной суммы значений ДН в S направлениях может быть записан в следующем виде:

Здесь * - знак комплексного сопряжения скалярной величины и эрмитова сопряжения матрицы; через [А] обозначена квадратная эрмитова матрица N-го порядка с элементами

Аналогично можно записать и для знаменателя (8)

где [В] - квадратная эрмитова матрица N-го порядка с элементами

В итоге оптимизируемый функционал (8) может быть приведен к виду

Поскольку матрицы [А] и [B] эрмитовы, то K(J) является отношением эрмитовых форм. Входящие в (16) эрмитовы формы определяют пучок форм

который является регулярным, так как форма |J〉*[В]·|J〉 положительно определена, что обусловлено ее физическим смыслом.

Максимум (16) равен наибольшему характеристическому числу пучка форм (17), причем этот максимум достигается только на соответствующем этому числу главном векторе пучка [2].

В соответствии с [2] максимальным собственным значением пучка эрмитовых форм (17) является максимальное собственное значение матрицы [D], определяемой как

а собственный вектор, соответствующий максимальному собственному значению матрицы [D], и будет решением задачи оптимизации (8).

Максимальное собственное значение и соответствующий ему собственный вектор матрицы [D] могут быть определены одним из известных способов, например QR разложения [3]. Однако в данном случае можно поступить проще. Поскольку ранг матрицы [А] равен единице, то вектор токов, доставляющий максимум функционалу (16), может быть найден аналитически из выражения [4]

Работа устройства, функционирующего по предложенному способу, может быть проиллюстрирована с помощью фиг.1. Информация о направлениях ϕ_s максимумов формируемых лепестков и соответствующих весах w_s поступает на входы 1 и 2 вычислителя КВК 3, функционирующего в соответствии с выражением (19). Принятые каждым излучателем 4 сигналы взвешивают с помощью устройств комплексного взвешивания 5 в соответствии с КВК, определяемыми вычислителем 3, после чего они поступают на входы высокочастотного сумматора 6. В результате на выходе 7 высокочастотного сумматора 6 формируется диаграмма направленности f(ϕ), имеющая S лепестков (“лучей”) с относительными уровнями w_s.

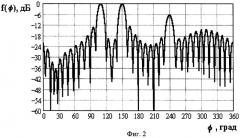
В качестве примера на фиг.2 приведена трехлепестковая ДН, сформированная кольцевой АР с изотропными излучателями при следующих исходных данных: число излучателей N=36, шаг решетки λ/2, углы ориентации лепестков ДН ϕ₁=110°, ϕ₂=150°, ϕ₃=240°, весовые коэффициенты w₁=1, w₂=1, w₃=0.5.

При проведении расчетов диаграммы направленности элементов принимались в виде

где ϕ_n - угловая координата n-го излучателя.

Комплексные амплитуды токов в элементах АР находились как с помощью выражения (18), т.е. через определение собственных чисел и собственных векторов матрицы D, так и с помощью выражения (19). Как и следовало ожидать, оба пути приводят к одному и тому же результату. Из фиг.2 видно, что положения “лучей” (лепестков) ДН и их уровни соответствуют заданным.

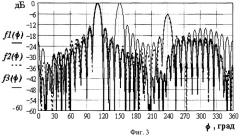
На фиг.3 продемонстрирована возможность последовательного формирования с помощью алгоритма (19) однолепестковой (f1(ϕ)), двухлепестковой (f2((ϕ)) и трехлепестковой (f3(ϕ)) ДН. В первом случае формируется лепесток с номером s=1 (т.е. с весом w₁ и ориентацией ϕ₁), во втором - лепестки с номерами 1 и 3, а в третьем - все три лепестка, приведенные на фиг.1.

Таким образом, изменение режима выполнения операции взвешивания, проявившееся в том, что при определении главного вектора пучка эрмитовых форм используют информацию о направлениях ориентации лепестков диаграммы направленности и их относительном уровне, а в качестве первой эрмитовой формы пучка выбирают квадрат модуля взвешенной суммы значений диаграммы направленности в направлениях формируемых лепестков, обеспечивает формирование многолепестковых диаграмм направленности с заданными положениями и уровнями основных лепестков.

Источники информации

1. Э.И.Крупицкий. О максимальной направленности антенн, состоящих из дискретных излучателей // Доклады АН СССР, 1962, т.143, №3, с.257-259.

2. Ф.Р.Гантмахер. Теория матриц. - 4-е изд. - М.: Наука, гл. ред. физ-мат. лит., 1988, 552 с.

3. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, гл. ред. физ-мат. лит., 1984, 320 с.

4. Cheng David К. Optimization techniques for antenna arrays, "Proc. IEEE", 1971, 59, №12, 1664-1674.

Способ формирования многолепестковых диаграмм направленности антенной решетки, основанный на взвешивании сигналов, принятых каждым излучателем, и последующем их суммировании, при котором комплексные весовые коэффициенты находят как главный вектор пучка эрмитовых форм, соответствующий наибольшему характеристическому числу пучка, причем в качестве второй эрмитовой формы пучка выбирают среднее значение диаграммы направленности по мощности, отличающийся тем, что при определении главного вектора пучка эрмитовых форм используют информацию о направлениях ориентации основных лепестков диаграммы направленности и их относительном уровне, а в качестве первой эрмитовой формы пучка выбирают квадрат модуля взвешенной суммы значений диаграммы направленности в направлениях формируемых лепестков.