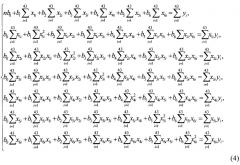Способ контроля тепловыделения пчелиной семьи в пассивный период

Способ контроля тепловыделения пчелиной семьи в пассивный период

Иллюстрации

Показать все

Реферат

Изобретение относится к сельскому хозяйству и может быть использовано в пчеловодстве, предназначено для контроля тепловыделения пчелиной семьи во время зимовки.

Известно, что исход зимовки зависит от энергетических затратах пчелиной семьи. Известные методы оценки тепловыделения пчелиной семьи основаны на использовании косвенных показателей, например по количеству потребляемого кислорода и выделяемой углекислоты. Метод позволяет с достаточной точностью определить энергетические затраты пчелосемьи, но очень сложен [1].

Наиболее близким по технической сущности к изобретению является способ контроля тепловыделения пчелиной семьи во время зимовки пчел, основанный на моделировании процесса тепловыделения членами пчелиной семьи. Суть способа состоит в том, что для генерации тепла применен генератор тепла, изготовленный с использованием пластин размером 430Х30Х1,5 мм, расположенных между сотовыми рамками в улье без пчел. Нагрев пластин (электроподогревателей) происходит за счет электрического тока. Его автоматическое включение происходит в тот момент, когда температура над рамками модели опускается ниже, чем в той же точке над контролируемым пчелиным гнездом, заселенного улья [2, 3].

Недостаток этого способа заключается в его сложности (необходимо построить автоматическую следящую систему, отслеживающую все изменения температуры в контрольном улье с пчелами, и регулирующую нагрев улья без пчел, с одновременной непрерывной регистрацией и температуры, и электрической энергии, затрачиваемой на нагрев улья без пчел), и большой длительности эксперимента (в течение всей зимовки). При этом определяется тепловыделение только одной конкретной пчелиной семьи. Распространять полученные результаты на другие семьи практически невозможно как в силу больших различий в силе пчелиных семей, так и из-за существенных различий теплообмена различных ульев с окружающей средой.

Технической задачей, на решение которой направлено предлагаемое изобретение, является упрощение процесса контроля тепловыделения и возможность одновременного контроля тепловыделения нескольких пчелиных семей.

Решение указанной задачи достигается тем, что первоначально изготавливают модель теплогенератора с применением электроподогрева, которую выполняют из пластин, помещаемых в улей без пчел в межсотовое пространство, вокруг этой модели располагают на равных расстояниях от рамок с сотами термодатчики, изменяют внешнюю температуру в пределах температур зимовки, изменяют мощность теплогенератора, одновременно измеряя ее, и проводят периодический замер температур термодатчиков, а затем, используя многомерный регрессионный анализ, определяют математическую модель в виде где у(х) - значения мощностей теплогенератора, x_i - значения температур, b_i - значения коэффициентов устанавливаемых экспериментально, которая связывает выделяемую мощность теплогенератора в точках размещения термодатчиков внутри улья и внешней температурой, а в последующем, имея эту математическую модель для определения тепловыделения пчелиных семей в ульях пасеки, проводят замеры температур вокруг пчелиных клубов, где термодатчики размещены в тех же точках, как в улье с электрическим теплогенератором и, подставив измеренные значения температур, а также значение наружной температуры, вычисляют тепловыделение каждой контролируемой пчелиной семьи.

Для построения математической модели, по которой можно будет определить тепловыделение пчелиной семьи, был применен многомерный регрессионный анализ [4]. Уравнение регрессии, которое будет представлять математическую модель для определения тепловыделения пчелиной семьи представляется следующим выражением

где у(х) - значения мощностей теплогенератора, x_i - значения температур, b_i - значения коэффициентов устанавливаются экспериментально.

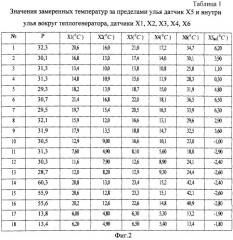
Необходимо определить коэффициенты b₀, b_i,... , b_m. Исходными данными является выборка из многомерной совокупности мощности и температур, которые приведены в табл.1 (фиг.1), приведенного примера. Эти значения представляют матрицу температур Х и вектора Y, соответствующих мощностям тепловыделения модели теплогенератора:

Диапазон вариаций мощности, потребляемой теплогенератором, и наружной температуры в экспериментальных данных должен перекрывать реальные диапазоны вариаций этих величин, а число измерений n должно быть много больше числа определяемых коэффициентов регрессии. Далее для определения этих коэффициентов используется метод наименьших квадратов [4].

Составляют систему нормальных уравнений

которую можно решить любым способом, известным из линейной алгебры [4]. Для выборки табл.1 (фиг.2-фиг.4), которую можно считать, что она является нормально распределенной генеральной совокупностью необходимо проверить значимость оценок коэффициентов регрессии (табл.5, [4]). Также надо провести оценку значимости уравнения регрессии (1) (табл.4, [4]). После оценки значимости коэффициентов b₀...b_m уравнения регрессии и значимости самого уравнения регрессии полученное уравнение принимают к сведению, а вычисленным результатам по этому уравнению доверяют. В случае незначимости коэффициентов уравнения регрессии и отсутствия значимости самого уравнения регрессии число экспериментов увеличивают, проводят повторный перерасчет.

Пример. Для построения математической модели контроля тепловыделения пчелиной семьей в качестве теплогенератора были применены электронагреватели, расположенные между рамок с пчелиными сотами. На равных расстояниях и в разных местах фиг.1 были размещены термодатчики, с помощью которых осуществлялся съем температуры на измерительный прибор.

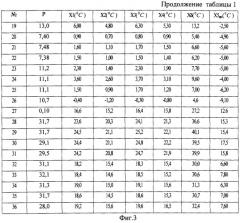
Измеренные значения температур после каждого изменения мощности регистрировались после установления термодинамического равновесия в пространстве вокруг рамок (когда показания соответствующих термодатчиков переставали изменяться). Эксперимент проводился с 10-рамочным ульем системы Дадан. Все экспериментальные данные приведены в табл.1 (фиг.2-фиг.4).

В ходе проведения эксперимента измерялось напряжение электропитания, подаваемое на нагревательные элементы. По известному сопротивлению нагревательных элементов для каждого измеренного напряжения определяли мощность. Внешняя температура Х5 за время эксперимента варьировалась в пределах от -9° С до +17° С.

С помощью температурных датчиков XI-Х4, Х6 регистрировали значения температур вокруг рамок с сотами, между которыми устанавливались электроподогреватели фиг1.

Для составления системы уравнений согласно экспериментальным данным табл.1 (фиг.2-фиг.4), была определена мощность тепловыделения Р и суммы произведений мощности на температуры Рх1, Рх2, Рх3, Рх4, Рх5,

Рх6_внешн., табл.2 (фиг.5-фиг.7), суммы квадратов температур , , , , , табл.3 (фиг.8-фиг.10), суммы произведения температур х₁х₂, х₁х₃, х₁х₄, x₁x₅, x₁x₆, х₂x₃, х₂x₄, х₂x₅, х₂x₆, х₃x₄, х₃x₅, х₃x₆, х₄x₅, х₄x₆, х₅x₆, табл. 4 (фиг.11-фиг.16)

С использованием полученных экспериментальных данных табл. 1 (фиг.2-фиг.4) и вычисленных данных табл.2-табл.4 (фиг.5-фиг.16) составлена система уравнений:

На базе составленной системы уравнений (4) с использованием табличных данных табл.1-табл.4 (фиг.5-фиг.16) были определены коэффициенты b_o, b₁, b₂, b₃, b₄, b₅, b₆. Полученные значения коэффициентов были подставлены в уравнение регрессии (1), было получено уравнение регрессии (5):

Для проверки значимости уравнения регрессии (5) была проведена оценка остаточной дисперсии. Для этого, используя уравнение регрессии (5) для каждого значения температур х₁ х₂ х₃ x₄ x₅ х₆, приведенных в табл.1 (фиг.2-фиг.4), вычислена величина у(х_i). Все вычисления сведены в табл.5 (фиг.17-фиг.19). Проверена нулевая гипотеза H₀:β *=0. Вычислена статистика F=(Q₁/Q_оcm)(k₂/k₁). Согласно табл. 5 (фиг.17-фиг.19) Q_ocm=792,35, Q=7941,08; отсюда Q₁=Q-Q_ocm=7148,73. Число степеней свободы: k₂=n-m-1=38, k₁=m=6. Тогда F=(7148,73*38)/792,35*6=57,1. По табл.4 [4] приложений для уровня значимости α =0,05 критическое значение F_(0,05;6;38)=2,34. Т.е. 57,1>2,34, следовательно, вычисленное уравнение регрессии (5) значимо.

Были проведены дополнительные опыты. Замерены температуры и мощность. Затем по полученным дополнительным экспериментальным данным (температурам) с применением уравнения регрессии (5) вычислили мощности тепловыделения и сравнили с реальной, имевшейся на теплогенераторе. Результаты дополнительного опыта приведены в табл. 6 (фиг.20). Согласно этому опыту установлено, что даже при других вариантах температур, не вошедших в табл.1 (фиг.1), вычисляемая мощность по регрессионной модели (5) и реальная замеренная имеют близкие значения.

Данная математическая модель получена для системы улья Дадан 10-рамочный позволяет достаточно точно установить тепловыделение пчелиной семьи в пассивный период ее жизнедеятельности.

Таким образом, предлагаемый способ контроля тепловыделения пчелиной семьей в пассивный период позволяет без применения аппаратных средств, а только по замерам температур контролировать тепловыделения пчелиных семей всей пасеки. Найдет применение в практическом пчеловодстве при компьютеризации пасек и при оснащении ульев с пчелами термодатчиками. Контроль тепловыделения всех ульев пасеки позволит оптимально организовать зимовку пчел.

Источники информации

1. Еськов Е.К. Микроклимат пчелиного жилища // Москва. Россельхозиздат. 1983.

2. Пат. № 1477346. Способ контроля функционального состояния пчелиной семьи в пассивный период ее жизнедеятельности и устройство для его осуществления // Опубл. 07.05.89. Бюл. № 17 (прототип).

3. Еськов Е.К. Управление процессами жизнедеятельности медоносных пчел и их оптимизация / Методические указания //Москва. 1982.

4. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. / Математическая статистика. // Москва "Высшая школа", 1981, (стр. 269-274).

Способ контроля тепловыделения пчелиной семьи в пассивный период, заключающийся в экспериментальном исследовании распределения температуры в улье без пчел, с размещенным внутри него теплогенератором с электроподогревом, который выполняют из пластин, помещаемых в улей в межсотовое пространство, отличающийся тем, что термодатчики располагают на равных расстояниях сверху и с боков теплогенератора, при изменениях внешней температуры в пределах температур зимовки изменяют мощность теплогенератора в пределах реально возможной для пчелосемьи, и после установления термодинамического равновесия в ульевом пространстве проводят замер показаний термодатчиков, а затем определяют математическую модель в виде линейного уравнения регрессии, связывающего выделяемую мощность теплогенератора с температурой в точках размещения термодатчиков внутри улья и внешней температурой, а в последующем, имея эту математическую модель, проводят замеры температур вокруг пчелиных клубов, где термодатчики размещены в тех же точках, как в улье с теплогенератором и, подставив измеренные значения температур, а также значение наружной температуры в полученное уравнение регрессии, вычисляют тепловыделение каждой контролируемой пчелиной семьи.