Способ снижения сопротивления трения тела посредством формирования вязкоупругого покрытия

Способ снижения сопротивления трения тела посредством формирования вязкоупругого покрытия

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение относится к способу разработки вязкоупругого покрытия для снижения сопротивления трения в турбулентном потоке жидкости.

Предшествующий уровень техники

Вязкоупругое покрытие поглощает энергию из турбулентного потока и модифицирует механизм обмена энергии между стенкой и потоком, в результате чего изменяется локальный профиль скорости и развитие пограничного слоя. С изменением профиля скорости вблизи стенки также снижается частота турбулентных выбросов и уменьшается диссипация энергии турбулентности с удалением от стенки, что дает снижение сопротивления трения порядка 30%.

Если колебания поверхности вязкоупругого покрытия малы, меньше, чем толщина вязкого подслоя турбулентного пограничного слоя (ТПС), то возмущения, генерированные в жидкости колеблющейся поверхностью, будут оставаться возле стенки внутри вязкого подслоя. Методика определения подходящих параметров вязкоупругого покрытия для снижения его сопротивления рассматривает и развитие ТПС при заданных граничных условиях для скорости, и обмена энергии на поверхности, и деформацию поверхности, и поглощение энергии вязкоупругим слоем при заданном поверхностном поле давления, моделирующем ТПС.

С тех пор как M.O.Крамер заявил об успешных результатах экспериментов в 1957 году, был предпринят ряд попыток снизить сопротивление трения в жидком турбулентном потоке на поверхности, применяя пассивные податливые покрытия. Экспериментальные данные в этой области были разнородными. Большинство исследователей получили повышение сопротивления, и только несколько заявили о снижении сопротивления в турбулентном потоке. Множество теоретических исследований характеризовали устойчивость ламинарного пограничного слоя на деформируемой поверхности, другие характеризовали реакцию покрытия на пульсационную нагрузку.

Однако до сих пор не было предложено способа разработки вязкоупругих покрытий для снижения упругого сопротивления трения, успешно снижающего сопротивление в турбулентном потоке.

В прошлом пассивные покрытия тестировались без задания полной системы критических физических параметров, таких как модуль сдвига, зависящий от частоты, плотность и толщина. Для того чтобы достичь достоверного снижения сопротивления с помощью вязкоупругого покрытия, нужна методика подбора подходящих свойств материала и оценки ожидаемого снижения сопротивления как функции геометрии и скорости.

Соответствующая информация по связанным техническим вопросам имеется и может быть полезна. Классическое обсуждение теории пограничного слоя, включая формулировку уравнений Навье-Стокса и уравнений турбулентного пограничного слоя, представлено в Boundary-Layer Theory, Dr. Hermann Schlichting, опубликованное McGraw Hill, New York, seventh edition, 1979. Описание структуры и масштабов в турбулентных потоках приведено в Turbulence, 1975, McGraw Hill, автор J.O.Hinze, и в “Coherent Motions in the Turbulent Boundary Layer”, в Annual Review of Fluid Mechanics, 1991, том 23, стр.601-39, автор Steven K.Robinson. Обоснование моделей турбулентности типа напряжений Рейнольдса раскрыто в главе “Turbulent Flows: Model Equations and Solution Methodology”, автор Tom Gatski, включенной в Handbook of Computational Fluid Mechanics, опубликованное Academic Press в 1996. Уравнения в механике жидкости и твердого тела часто выражены в индексной или тензорной форме, для краткости. Глава 2 в тексте A First Course in Continuum Mechanics, Y.C.Fung, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1977, дает краткое введение в тензорные обозначения и уравнения механики. Введение в конечно-разностные методы, которые используются для решения системы уравнений импульсов и неразрывности, представлено в Computational Fluid Dynamics for Engineers, Klaus Hoffman, и опубликованном the Engineering Education System in Austin, Texas в 1989.

Описание измеренных и математически моделированных физических свойств полимеров дано в Viscoelastic Properties of Polymers, J.D.Ferry, Wiley, New York, 1980, третье издание. В статье “Loss Factor Height and Width Limits for Polymer Relaxation”, Bruce Hartmann, Gilbert Lee, and John Lee, Journal of the Acoustical Society of America, Vol.95, No.1, January 1994, обсуждается математическое описание модулей сдвига для реальных вязкоупругих полимерных материалов, включая моделированные в соответствии с подходом Havriliak-Negami.

Недавно в публикации K.S.Choi, X.Yang, B.R.Clayton, E.J.Glover, M.Atlar, B.N.Semonev, and V.M.Kulik, “Turbulent Drag Reduction Using Compliant Surfaces”, Proceedings of the Royal Society of London, 1997, 453, pp.2229-2240 сообщалось об экспериментальных измерениях снижения турбулентного сопротивления трения до 7% на осесимметричном теле, покрытом вязкоупругим материалом.

Эти эксперименты были выполнены в Великобритании и использовали покрытия, разработанные и изготовленные в Новосибирском Институте теплофизики Российской Академии Наук группой, возглавляемой Б.Н. Семеновым. Подход к разработке является полуэмпирическим и не учитывает характеристики комплексного модуля сдвига вязкоупругого материала, в частности время релаксации материала. Этот подход не учитывает зависимости свойств материала от частоты колебаний. Более того, концепция Семенова справедлива только для мембранных покрытий, таких как пленка, состоящая из вспененной резины, пропитанной водой или глицерином, где рассматриваются только нормальные к поверхности колебания.

Структура покрытия, предназначенного для снижения сопротивления, рассматривалась в литературе, начиная с патента Германии 1938 г., No.669-897, “An Apparatus for the Reduction of Friction Drag”, на имя Крамера. Позднее Kрамером получены патенты 3161385 и 3585953, для покрытий, продлевающих ламинарный пограничный слой. В советских авторских свидетельствах: USSR 1413286 “A Damping Covering”, 1974; USSR 1597866 “An Adjustable Damping Covering”, 1978, и USSR 1802672 “A Damping Covering for Solid Bodies”, 1981 также описаны структуры снижающих сопротивление покрытий, содержащих вязкоупругие материалы. Эти авторские свидетельства идентифицируют трехмерную структуру в снижающих сопротивление покрытиях, но не рассматривают способ для определения подходящих параметров вязкоупругого материала, который можно было бы использовать при изготовлении таких покрытий. Структурные свойства включают многослойные материалы, продольные включения типа ребер из упругих, вязкоупругих или жидких материалов, подогреваемые элементы. Вязкоупругие покрытия могут быть скомбинированы с другими формами структуры, такими как продольные ребра, сформованные на или внутри поверхности покрытия. Как описано в публикациях, таких как “Secondary Flow Induced by Riblets”, автор D.B.Goldstein и T.C.Tuan, опубликованной в Journal of Fluid Mechanics, volume 363, 25 May 1998, стр.115-152, двухмерные жесткие ребра сами по себе показали в эксперименте снижение сопротивления трения до 10%.

Краткое изложение существа изобретения

В основу настоящего изобретения поставлена задача создания способа разработки вязкоупругих покрытий для снижения турбулентного сопротивления трения, который позволяет разрабатывать вязкоупругие покрытия, обеспечивающие снижение турбулентного сопротивления трения.

Покрытия со свойствами материала, разработанного согласно способу, раскрытому в этом изобретении, снижают сопротивление трения более чем на 10%. Способ позволяет определять зависящий от частоты комплексный модуль сдвига, плотность и толщину изотропного вязкоупругого материала, который будет снижать турбулентное сопротивление трения относительно конкретных условий потока на жесткой поверхности.

Изобретение позволяет оценить количественно уровень снижения сопротивления. Приведены примеры для турбулентного течения на жесткой гладкой пластине, а также на гладкой вязкоупругой пластине, где учитываются и нормальное и продольное колебания поверхности.

Согласно изобретению раскрыты свойства покрытия, составленного из нескольких слоев изотропных вязкоупругих материалов или из анизотропных материалов, а также минимизированы эффекты кромки для покрытий конечной длины. Изобретение позволяет стабилизировать продольные вихри посредством комбинации конструкции вязкоупругого покрытия с дополнительными элементами, такими как ребра.

При взаимодействии турбулентного пограничного слоя (ТПС) с вязкоупругим (ВУ) слоем осуществляется:

1) определение параметров турбулентного пограничного слоя при данных граничных условиях для жесткой, упругой или вязкоупругой поверхности, и

2) определение реакции вязкоупругой или упругой поверхности на периодическую возмущающую функцию, которая аппроксимирует нагрузку турбулентного пограничного слоя.

Согласно изобретению осуществляют определение амплитуд и скоростей колебания поверхности и потока энергии для вязкоупругого покрытия.

Эти две задачи связаны друг с другом коэффициентами, относящимися к граничным условиям на поверхности для поглощения энергии и амплитуд колебания поверхности (далее называемые динамическими и кинематическими граничными условиями соответственно). Определение ТПС решается сначала для жесткой поверхности, давая необходимые исходные данные для описания возмущающей функции на поверхности, а также исходные значения сопротивления трения для сравнения. Далее решается ВУ проблема при заданной периодической возмущающей функции, которая аппроксимирует пульсации сдвига и давления в пограничном слое. Начальный выбор параметров материала основан на теоретических и эмпирических соображениях. Оптимальные параметры материала выбираются в результате последовательных приближений так, что удовлетворяются следующие критерии:

1) поток энергии в вязкоупругое покрытие максимальный, и

2) амплитуды колебаний поверхности меньше, чем толщина вязкого подслоя турбулентного пограничного слоя на покрытии.

Если амплитуды колебания превышают толщину вязкого подслоя турбулентного потока, то колебания существенно усиливают шероховатость поверхности, приводя к увеличению сопротивления трения. Более того, поскольку фазовая скорость возмущений в пограничном слое превосходит скорость сдвиговой волны в материале, возникает резонансное взаимодействие с большими амплитудами волны. Такие условия нужно избегать.

Однако умеренный поток энергии в материал, когда энергия трансформируется во внутренние сдвиговые волны и в конечном итоге рассеивается как тепло, приводит к качественным и количественным изменениям в балансе энергии с соответствующим снижением сопротивления трения. Оптимальные физические свойства вязкоупругого материала будут изменяться со скоростью набегающего потока, положением вдоль тела, градиентом давления и другими факторами, которые влияют на развитие пограничного слоя и характеристики локальных турбулентных пульсаций.

При решении ТПС уравнений можно количественно оценить турбулентное сопротивление трения на вязкоупругой, упругой или жесткой поверхности. В случае вязкоупругой поверхности, где энергия поглощается и поверхностные колебания ненулевые, задаются динамические и кинематические граничные условия. Эти граничные условия выводятся из решения ВУ уравнений для потока энергии и амплитуд колебания поверхности, и затем переносятся в граничные условия для диссипации и напряжений Рейнольдса для решения ТПС уравнений.

Вертикальные колебания влияют на эффективную шероховатость поверхности, и среднеквадратичное значение вертикального колебания классифицируется как динамическая шероховатость. Если амплитуды колебания меньше, чем толщина вязкого подслоя, то можно оценивать напряжения Рейнольдса как нулевые. Уравнения турбулентного пограничного слоя описывают турбулентную диффузию как градиентное приближение, которое вмещает динамическое граничное условие. Вводятся функции для описания перераспределения энергии турбулентности в пристенном районе для различных поверхностей.

Краткое описание чертежей

В дальнейшем изобретение поясняется описанием предпочтительных вариантов его воплощения со ссылками на сопровождающие чертежи, на которых:

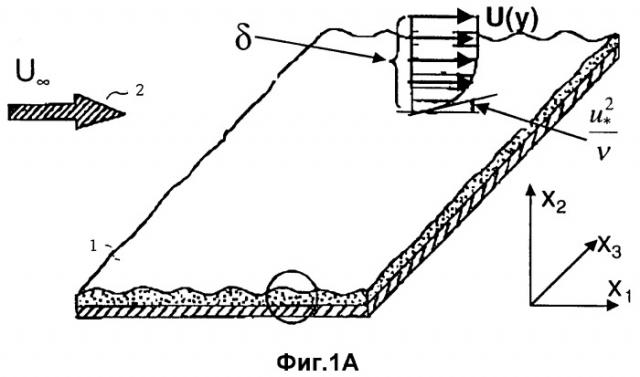
фиг.1А изображает схему взаимодействия пассивного вязкоупругого покрытия с турбулентным пограничным слоем, где низкоамплитудная бегущая волна развивается на поверхности, согласно изобретению;

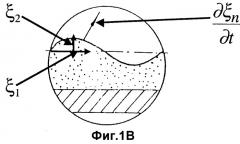
фиг.1В изображает участок внутри круга (масштаб увеличен), показанного на фиг.1А, и амплитуды смещения, согласно изобретению;

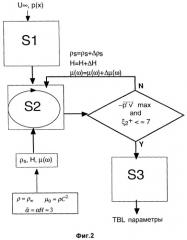
фиг.2 изображает блок-схему алгоритма способа для а) выбора вязкоупругого материала, который снижает турбулентное сопротивление трения при данных условиях потока, и б) количественной оценки снижения сопротивления относительно жесткой поверхности, согласно изобретению;

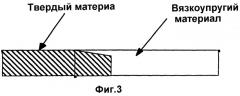
фиг.3 изображает элемент конструкции, введенный в область между вязкоупругим покрытием и жесткой поверхностью для уменьшения локальной амплитуды колебания и эффектов кромки, согласно изобретению.

Описание предпочтительных вариантов воплощения изобретения

Согласно изобретению определяют физические и геометрические параметры вязкоупругого покрытия, которое снижает сопротивление трения для данных условий потока. Изобретение позволяет оценить ожидаемую эффективность снижения сопротивления данного материала с известными физическими свойствами для тела данной конфигурации и определенных условий потока. Способ использовался для определения покрытий для турбулентного потока на плоских пластинах и осесимметричных телах и может быть также применен для тел более сложной геометрии с кривизной и градиентами давления.

Жидкий пограничный слой – это очень тонкий слой жидкости, прилегающий к поверхности, над которой течет жидкость. Это область, где силы трения играют главную роль и где поток перестраивается от условий на поверхности к условиям в свободном потоке. Внешний край пограничного слоя традиционно определяется как место, где отношение β средней скорости U к скорости свободного потока U∞ является константой, приблизительно равной 1:

Значение выбранной константы β зависит от конфигурации и соображений численной устойчивости. Для плоской пластины значение этой константы принимают равным 0,9975.

Турбулентный пограничный слой характеризуется спектром пульсаций давления и напряжения сдвига. Их частота, фазовая скорость и амплитудные характеристики являются функциями таких факторов, как скорость свободного потока, конфигурация тела, условия на поверхности и градиент давления. В случае жесткой поверхности движения на поверхности нет. Для упругой или вязкоупругой поверхности, пульсации давления и сдвига на стенке действуют как возмущающая функция, которая деформирует поверхность, создавая поверхностные волны. Для вязкоупругой поверхности энергия из турбулентного пограничного слоя может быть поглощена и диссипирована покрытием, что требует правильного задания граничных условий на стенке для напряжения Рейнольдса и для поглощения энергии (т.е. кинематических и динамических граничных условий).

На фиг.1 представлена схема пассивного вязкоупругого покрытия, которое взаимодействует с турбулентным пограничным слоем толщины δ. Для простоты рассматривается поток со скоростью U∞ на покрытой пластине, где координаты x, y, и z соответствуют направлениям вдоль осей. Предполагается, что жидкость вязкая и несжимаемая и что материал покрытия вязкоупругий, т.е. обладает комбинацией упругих и вязких физических свойств.

Если поверхность жесткая, не будет колебаний и поглощения энергии. Если поверхность упругая или вязкоупругая, будут колебания поверхности и, если она вязкоупругая, будет также обмен энергией. Компоненты продольного и вертикального смещения поверхности вязкоупругого материала заданы как ξ ₁ и ξ ₂, и динамическая скорость определяется как:

где τ_w - это напряжение сдвига на стенке и ρ - плотность жидкости. Взаимодействие турбулентного пограничного слоя с вязкоупругим покрытием приводит к образованию квазипериодической поверхностной волны. Движение покрытия и поглощение им энергии (кинематические и динамические граничные условия), в свою очередь, влияют на баланс энергии в турбулентном пограничном слое и величину сопротивления трения, последняя из которых есть поверхностный интеграл напряжения сдвига на стенке.

Алгоритм операций заявленного способа представлен на фиг.2.

При взаимодействии турбулентного пограничного слоя (ТПС) с вязкоупругим (ВУ) слоем осуществляется определение:

1) параметров турбулентного пограничного слоя (ТПС), включая сопротивление трения на жесткой, упругой или вязкоупругой пластинах; и

2) поглощения энергии и амплитуд колебания вязкоупругой (ВУ) пластины, возбуждаемых периодической нагрузкой, которая аппроксимирует нагрузку турбулентного пограничного слоя.

Эти две части решения связаны друг с другом граничными условиями для энергии, поглощенной поверхностью, и для амплитуд движения поверхности и являются частью общего подхода выбора снижающих сопротивление покрытий и количественного определения снижения сопротивления при данных условиях потока. Ниже описываются эти две части решения.

Определение параметров турбулентного пограничного слоя на жесткой, упругой или вязкоупругой поверхностях (ТПС задача)

На фиг.2 ТПС параметры вначале определяются для жесткой поверхности – шаг S1, и затем определяются физические свойства вязкоупругого материала - шаг S3. На шаге S3 применяется тот же подход, что и на шаге S1, за исключением того, что динамические и кинематические граничные условия определяются по-другому. На жесткой поверхности нет движения и поглощения энергии. На упругой поверхности есть движение, но нет поглощения энергии. На вязкоупругой поверхности есть движение поверхности и поглощение энергии.

Общая система уравнений неразрывности, движения и энергии

Параметры турбулентного пограничного слоя определяются посредством решения системы уравнений неразрывности, движения и энергии с соответствующими граничными условиями. Эти уравнения выводятся из законов сохранения массы, сохранения количества движения (второй закон Ньютона) и баланса энергии (основанного на первом начале термодинамики).

В декартовых координатах общее уравнение неразрывности для сжимаемой жидкости с плотностью ρ и компонентами скорости U, V, и W в продольном, нормальном и трансверсальном направлениях:

Иначе уравнение 3 может быть записано в индексной форме (как в уравнении 4), где x, y, и z представлены как x₁, x₂, и x₃ соответственно, и U, V, и W представлены как U₁, U₂ и U₃ соответственно. Индекс i может иметь значения 1,2 или 3, и повторяющийся индекс i обозначает суммирование:

Уравнение 3 упрощается для несжимаемой жидкости, т.е. если плотность жидкости постоянна:

Обобщенные уравнения движения, называемые уравнениями Навье-Стокса, в случае несжимаемой жидкости с постоянной вязкостью выражаются в декартовых координатах:

где P - среднее давление;

g_i - вектор объемной силы вследствие внешних полей, таких как гравитация, которые действуют на элемент;

ν - кинематическая вязкость (константа).

Выражение 6а,b,c, записанное в индексной форме, представляет три уравнения для трех компонентов скорости в направлениях x, y, и z.

Компоненты турбулентной скорости могут быть описаны как сумма средней и пульсационной компоненты U_i и u' соответственно, где U₁, U₂, и U₃ эквивалентны U, V и W, а u'₁, u'₂, и u'₃ эквивалентны u', v', и w':

Черта сверху обозначает суммирование по времени:

Подставляя выражения 7а-7с в 6а-6с и осредняя по времени, получим следующую систему трех комплексных нелинейных уравнений движения турбулентного потока в частных производных второго порядка:

В уравнениях 9a-9c компоненты и называются нормальными напряжениями Рейнольдса, и компоненты в форме , , и называются сдвиговыми напряжениями Рейнольдса. Кинетическая энергия турбулентности k определятся как:

Замыкание обобщенной системы уравнений, включая уравнение 5 неразрывности и уравнения 9а–9с движения для турбулентного потока, требует семи дополнительных уравнений для определения шести напряжений Рейнольдса и скорости изменения турбулентной энергии k. Это изобретение определяет изотропную скорость диссипации ε, которая связана с переносом энергии в жидкости и через границу жидкость - поверхность. Уравнение переноса энергии основано на первом законе термодинамики, согласно которому изменение тепла dQ в объеме за время dt служит для изменения внутренней энергии dE и выполнения работы dWK:

В литературе существует множество подходов для вывода дополнительных уравнений для членов напряжений Рейнольдса. В заявленном изобретении используют перенос напряжений Рейнольдса, которые принимают следующую общую форму:

где P_ij - порождение, П_ij - тензор корреляций давление-напряжение, J_ijk - диффузионный поток напряжений Рейнольдса и ε _ij - тензор диссипации.

В общем случае должны рассматриваться уравнения для всех шести компонент тензора напряжений Рейнольдса и для скорости диссипации. Уравнение для изотропной скорости диссипации ε схоже по структуре с уравнениями переноса напряжений Рейнольдса. Полные математические выражения для напряжений Рейнольдса и изотропной скорости диссипации будут представлены для отдельного случая двухмерного пограничного слоя.

Из вышесказанного следует, что уравнения, которые решаются для определения параметров турбулентного пограничного слоя, включают:

уравнение непрерывности 5,

три уравнения движения 9a,9b,9c,

шесть уравнений для сдвиговых и нормальных напряжений Рейнольдса 12a-12f, и

уравнение для изотропной скорости диссипации ε (16 ниже).

Для определения параметров турбулентного пограничного слоя осуществляют конечно-разностную аппроксимацию системы уравнений движения и неразрывности с соответствующими граничными условиями.

Уравнения турбулентного пограничного слоя

Полная математическая формулировка дана для частного случая несжимаемого турбулентного пограничного слоя в стационарном двухмерном осредненном потоке со скоростью U∞ . Уравнения двухмерного турбулентного пограничного слоя выводятся из общего уравнения неразрывности 5 и уравнений движения 9а-9с, в предположении, что:

Средняя трансверсальная скорость W равна нулю.

Гравитацией можно пренебречь.

Градиент давления в направлении y приблизительно равен нулю.

Средняя скорость U в продольном направлении намного больше, чем средняя скорость V в нормальном направлении.

Скорость изменения параметров в направлении x намного меньше, чем скорость изменения параметров в направлении y.

Вышеперечисленные предположения позволяют сделать упрощение для системы уравнений, нужных для нахождения параметров турбулентного пограничного слоя, которое будет включать модифицированное уравнение неразрывности (13):

и уравнение движения для компоненты скорости U 14:

В общем случае, когда нужны уравнения переноса для шести компонент тензора напряжений Рейнольдса, сдвиговые напряжения Рейнольдса и предполагаются пренебрежимо малыми, так что только уравнения для , и формулируются в формате уравнения (12) (повторяемого ниже как уравнения 15а-15d):

где P_ij – член порождения, П_ij - тензор корреляций давление-напряжение, J_ijk - диффузионный поток напряжений Рейнольдса, и ε _ij - тензор диссипации. Пятое уравнение для ε такое:

где выражение для вязкой диффузии может также моделироваться как:

если это нужно для численной устойчивости решения для вязкоупругих неколеблющихся поверхностей в пристенной области.

В уравнениях 15a-15d член P_ij можно выразить как:

В уравнении 16 член P_Σ можно выразить как:

Тензор П_ij корреляций давление-напряжение, который перераспределяет энергию между различными компонентами напряжений Рейнольдса, можно выразить как:

где представляет пристенное перераспределение турбулентной энергии от продольной компоненты к нормальной и трансверсальной, представляет пристенное изменение компонентов тензора порождения напряжений Рейнольдса, и представляет пристенное перераспределение турбулентной энергии пропорционально локальной завихренности:

Здесь - это однозначная демпфирующая функция в пристенной области:

где

и

Здесь D_ij – тензор диффузии:

- градиент турбулентного и вязкого потока напряжений Рейнольдса в пограничном слое, где только один компонент остается в погранслойном представлении:

где A равно 6 в уравнениях для А равно 2 для и и А равно 4 для (т.е. эффективные градиенты диффузии различны для разных компонентов напряжений Рейнольдса), и коэффициент турбулентной диффузии, ε _t равен:

за исключением уравнения 16, где

Тензор диссипации, , записывается как:

где характеризует поток в пристенной области:

и

Уравнение 16 включает две функции и которые также вносят поправки в пристенный поток:

Значения констант для потока на плоской пластине

приведены в таблице 1.

Таблица 1
С1	C2	Cε1	Cε2	Ct	Cε	C1'	C2'	C3'
1,34	0,8	1,45	1,9	0,12	0,15	0,36	0,45	0,036

Для случая двумерного пограничного слоя параметры турбулентного пограничного слоя при различных координатах x и y определяются из решения уравнения 13 неразрывности, уравнений 14 движения в направлении x, уравнений 15а–15d переноса для напряжений Рейнольдса и , и уравнения 16 скорости изотропной диссипации энергии, при заданных граничных условиях. Задача решается численно с использованием конечно-разностной аппроксимации. Все уравнения приводятся к стандартному виду параболического уравнения с заданной функцией, и решение получается в точках расчетной сетки в системе координат (x,y).

Граничные условия – это значения параметров на границах пограничного слоя, т.е. на поверхности и в свободном потоке. Скорость свободного потока равна U∞ . Граничные условия на поверхности задаются для нормальных и сдвиговых напряжений Рейнольдса (кинематические граничные условия), а также для изотропной скорости диссипации (динамические граничные условия). Для произвольной геометрии должны быть заданы координаты поверхности x и y. Если поверхность плоская, граничные условия задаются на линии y=0.

Поскольку амплитуды колебания на поверхности малы, можно применять линеаризованные кинематические граничные условия, при которых средние скорости на поверхности полагаются нулевыми. Граничные условия для пульсационных компонентов скорости на поверхности плоской пластины выражаются как:

где и - это продольное и вертикальное смещения поверхности соответственно, - динамическая скорость (определенная выше) и - угол наклона среднего потока к продольной оси в плоскости x₁-x₃. При линеаризованных граничных условиях средние скорости на поверхности полагаются нулевыми. Смещения поверхности аппроксимируются первыми модами ряда Фурье:

где α_e – это волновое число, соответствующее максимуму энергии в пограничном слое, оно равно:

где энергонесущая частота ω_e:

и фазовая скорость, соответствующая энергонесущим возмущениям в пограничном слое, предполагается такой:

Поскольку существует диапазон частот, на которых существует перенос энергии, как отражено в научной литературе, полезно также выполнить вычисления для случая, когда:

В отсутствии резонанса целесообразно осреднять по времени компоненты напряжений Рейнольдса на стенке:

где - это среднеквадратичная амплитуда смещения.

Для пассивного изотропного вязкоупругого покрытия, возбуждаемого вынужденной нагрузкой, реакция приобретает форму бегущей волны, так что сдвиг фаз между нормальным и продольным смещением будет около , и сдвиговое напряжение Рейнольдса на поверхности будет нулевым. Для анизотропных материалов сдвиг фаз может быть другим, так что на стенке могут генерироваться отрицательные сдвиговые напряжения Рейнольдса. Для жесткой стенки движения на стенке не будет, так что нормальные и сдвиговые напряжения Рейнольдса будут равны нулю.

Граничное условие для изотропной скорости диссипации:

где первый член отражает вязкую диссипацию и второй – поглощение энергии вязкоупругим материалом. Для жесткой поверхности на стенке нет поглощения энергии и второй член равен нулю. Поглощение турбулентной энергии покрытием эквивалентно и может быть аппроксимировано выражением которое является диффузионным потоком энергии через границу и характеризуется с помощью градиентного механизма для турбулентной диффузии. Это выражение динамического граничного условия совместимо с методологией переноса напряжений Рейнольдса для замыкания модели турбулентности.

Уравнения 13,14, 15a-15d и 16 решаются для компонент средней скорости, нормальных и сдвиговых напряжений Рейнольдса и диссипации энергии при заданных динамических и кинематических граничных условиях (уравнения 44-48), основанных на решении вязкоупругой задачи (описано в следующем разделе). Эта задача решается численно, используя конечно-разностные аппроксимации параболических уравнений. Сопротивление трения тела с вязкоупругим покрытием вычисляется как интеграл напряжения сдвига на стенке τ_w по всей поверхности тела:

для двумерного тела, и - динамическая вязкость. Сравнение результатов с вычисленными для жесткого тела такой же геометрии при таких же граничных условиях дает оценку ожидаемого снижения сопротивления трения.

Чтобы снизить сопротивление трения, необходимо минимизировать амплитуды колебания поверхности и обеспечить максимальный поток турбулентной энергии из потока в покрытие . Если амплитуды колебания поверхности ξ

+

2

не превышают толщину вязкого подслоя:

то нормальные напряжения Рейнольдса на границе (уравнения 44-46) могут считаться нулевыми. Для покрытия, которое поглощает энергию с низким уровнем колебания, напряжения сдвига в пристенной области уменьшаются, и также уменьшается порождение турбулентности в пограничном слое. Для покрытия, которое колеблется с амплитудой, большей вязкого подслоя, поверхность может действовать как элемент динамической шероховатости и тем самым увеличивать уровень турбулентности, генерируемой в пограничном слое.

Реакция вязкоупругого материала на турбулентный пограничный слой (ВУ задача)

Способ позволяет также определить реакцию вязкоупругого материала на турбулентный пограничный слой (шаг S2). Для жесткой поверхности напряжения Рейнольдса (уравнения 44-47) на поверхности равны нулю и изотропная скорость диссипации содержит только вязкий член. Однако для вязкоупругого материала кинематические и динамические граничные условия определяются из решения двумерного уравнения сохранения количества движения для вязкоупругого материала:

где ρ_s – плотность материала; и - продольное и нормальное смещения по толщине покрытия; - амплитуда тензора напряжений. Тензор напряжений для вязкоупругого материала типа Фойгта-Кельвина записывается как:

где - тензор деформации:

и

- зависящая от частоты константа Ламе, которая определена в терминах объемного модуля сжатия