Способ определения коэффициента нелинейности показателя преломления оптических сред

Способ определения коэффициента нелинейности показателя преломления оптических сред

Иллюстрации

Показать все

Реферат

Величина коэффициента нелинейности показателя преломления n₂ является одной из важнейших характеристик оптических материалов, используемых для изготовления элементов тракта мощных лазерных систем. Наиболее важно знать значения n₂ собственно активной среды и стекла, из которого изготавливается основная масса остальных оптических элементов тракта (линзы, делительные зеркала и т.п.). Коэффициент нелинейности показателя преломления складывается из четырех составляющих (электронной, ядерной, стрикционной и термической), каждая из которых имеет свой механизм возникновения, инерционность и проявляется при своей определенной длительности взаимодействия электрического поля световой волны с нелинейной средой (электронная составляющая имеет время отклика ~10^-15 сек, ядерная - менее пикосекунды, стрикционная - порядка нескольких наносекунд, термическая - несколько микросекунд).

Изобретение относится к способам определений коэффициента нелинейности показателя преломления оптических сред.

Известен способ определения коэффициента нелинейности показателя преломления стекол, в котором образец облучают сфокусированным лазерным излучением, измеряют мощность излучения, падающего на образец, наблюдают наличие треков разрушения стекла вследствие мелкомасштабной самофокусировки излучения, определяют критическую мощность самофокусировки и вычисляют коэффициент нелинейности показателя преломления. (См. Journal of Quantum

Electronics, Vol.QE-9, No.11, November 1973, p.1054-1061). Способ позволяет учесть ядерную, электронную, стрикционную и тепловую составляющие коэффициента нелинейности показателя преломления. К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относится то, что в известном способе происходит разрушение исследуемых образцов в процессе измерения, а также то, что область применения ограничена измерением коэффициента нелинейности показателя преломления твердых сред.

Известен способ определения относительного коэффициента нелинейности показателя преломления, в котором два образца: исследуемый и эталонный с известной величиной коэффициента нелинейности показателя преломления, облучают импульсным лазерным излучением двух длин волн разной интенсивности, измеряют энергетические характеристики волн, падающих на образцы, в результате трехволнового взаимодействия получают сигнал на третьей длине волны, смещенной относительно первых двух по частоте, измеряют интенсивность сигнала на третьей длине волны для исследуемого образца и эталона и вычисляют относительный коэффициент нелинейности показателя преломления (См. Journal of Optical Society of America, Vol.4, No.6, June 1987, p.875-881). К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относится то, что в известном способе наличие сдвига частот, который не может быть менее 60 см^-1, ограничивает время взаимодействия поля с веществом величиной порядка 5· 10^-13 секунды, что, в свою очередь, ограничивает определение относительного коэффициента нелинейности показателя преломления только вкладом ядерной и электронной составляющих. Кроме того, этим методом принципиально невозможно произвести абсолютные измерения коэффициента нелинейности показателя преломления.

Наиболее близким по совокупности признаков способом того же назначения к заявленному изобретению является способ определения коэффициента нелинейности показателя преломления оптических сред, в котором образец облучают импульсным лазерным излучением пикосекундной длительности мощностью до 25 ГВт, с помощью фотоприемника с пикосекундным разрешением во времени регистрируют интерферограмму, полученную взаимодействием пучка, прошедшего образец, с неискаженным опорным пучком, измеряют мощность излучения, падающего на образец, и искривление полос интерферограммы, вычисляют коэффициент нелинейности показателя преломления (см. Journal of Applied Physics, Vol.47, №6, June 1976, p.2497-2501), принятый за прототип.

К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, принятого за прототип, относится то, что известный способ требует для наблюдения фазовых изменений волнового фронта прошедшего пучка, возникающих вследствие эффекта крупномасштабной самофокусировки, большой мощности падающего излучения, что, в свою очередь, накладывает ограничения на длительность импульса. Указанное ограничение приводит к тому, что с помощью известного метода, принятого за прототип, можно определить только ядерную и электронную составляющие коэффициента нелинейности показателя преломления, кроме того, из-за работы на режимах, близких к порогу разрушения стекла, существует опасность разрушения образца. Помимо этого, метод имеет существенную относительную ошибку измерений (20%) для сред с небольшим значением коэффициента нелинейности показателя преломления (например, кварц, ряд стекол типа кронов, фосфатные стекла и т.п.), и возможность повышения точности измерений также ограничивается порогом разрушения стекла. К недостаткам метода также можно отнести его сложность вследствие необходимости использования уникального дорогостоящего оборудования: интерферометр, фотоприемник с пикосекундным разрешением во времени, пикосекундный лазер большой мощности (с энергией в импульсе до 1 Дж).

Сущность изобретения заключается в следующем.

Изобретение направлено на решение задачи определения коэффициента нелинейности показателя преломления оптических сред без их разрушения и без ограничений на длительность импульса тестирующего излучения и агрегатное состояние тестируемой среды.

Технический результат, который может быть достигнут при осуществлении заявленного способа, заключается в определении коэффициента нелинейности показателя преломления с возможностью учета вклада всех (ядерной, электронной, стрикционной и тепловой) его составляющих, при небольшой (с точки зрения формирования нелинейных эффектов самовоздействия среды) мощности падающего излучения (до 1-2 ГВт), для оптических сред в любом агрегатном состоянии вещества без разрушения среды, а также повышение точности определения по сравнению с известными методами.

Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения коэффициента нелинейности показателя преломления оптических сред, включающем направление пучка лазерного излучения на оптическую среду, определение коэффициента нелинейности показателя преломления оптической среды, регистрируют пространственно-временное распределение интенсивности и определяют распределение фазы падающего излучения в плоскости, перпендикулярной направлению распространения излучения и являющейся плоскостью падения пучка на среду, регистрируют пространственно-временное распределение интенсивности излучения, прошедшего среду, в плоскости, расположенной за средой по ходу излучения и оптически сопряженной с плоскостью пространства, перпендикулярной направлению распространения излучения, и расположенной перед оптической средой, определение коэффициента нелинейности показателя преломления осуществляют расчетным путем из сравнения распределений для падающего на среду и прошедшего пучков.

При облучении исследуемой среды вследствие взаимодействия электромагнитного поля световой волны с веществом внутри образца возникают неоднородности показателя преломления, связанные с полем соотношением:

Δ n(r)=n₂·I(r),

где Δ n(r) - величина неоднородностей показателя преломления, зависящая от пространственной координаты r;

r - пространственная координата;

n₂ - коэффициент нелинейности показателя преломления;

I(r) - интенсивность световой волны внутри образца.

Наведенные неоднородности показателя преломления, в свою очередь, воздействуют на световую волну и вызывают фазовые деформации ее волнового фронта. Таким образом, возникает эффект аберрационного самовоздействия световой волны, проходящей сквозь исследуемую среду. В процессе дальнейшего распространения в такой световой волне происходит перераспределение интенсивности по сравнению с исходным распределением (например, наблюдается эффект крупномасштабной самофокусировки), и его можно зарегистрировать с помощью фотоприемника, например видеокамеры. Наиболее ярко этот эффект будет проявляться в пучках с большими перепадами интенсивности по поперечному сечению (например, пучков с Эйри-распределением, “гауссовских” и так называемых “супергауссовских” - с уплощенной вершиной и т.п.). Однако для этих пучков для любой плоскости регистрации распределения интенсивности, находящейся за средой по ходу луча, наблюдается сильная и статистически неустойчивая зависимость пространственного распределения интенсивности излучения от незначительных изменений энергии падающего пучка, что приводит к недопустимым погрешностям в измерениях. Нами обнаружено, что если регистрировать распределение интенсивности пучка, прошедшего среду, в плоскости, находящейся за средой по ходу излучения, но оптически сопряженной с плоскостью пространства, перпендикулярной направлению распространения и расположенной перед средой, этого удается избежать. Под оптическим сопряжением мы подразумеваем следующее из гауссовской общей теории оптических систем определение, что каждой точке пространства объектов соответствует в идеальной оптической системе точка пространства изображений, эти точки называются оптически сопряженными. Точно так же каждой прямой или плоскости пространства объектов должна соответствовать оптически сопряженная прямая или плоскость пространства изображений. Подход к указанному выше преобразованию прошедшего пучка при регистрации его распределения известен. Этого можно достичь, например, путем введения в пучок, прошедший среду, оптической системы, которая преобразует пучок таким образом, чтобы на плоскость регистрации, где расположен фотоприемник, находящуюся за средой по ходу луча, проектировалась некоторая плоскость пространства, ортогональная направлению распространения пучка и находящаяся перед средой.

При этом положение плоскости фотоприемника и оптически сопряженной с ней плоскости в пространстве объектов выбирается из соображений согласования параметров фотоприемника (например, таких как размер ПЗС-матрицы, ее разрешающая способность, число возможных градаций "серого" ("яркости") в изображении) и формируемого оптической системой изображения.

Распределение интенсивности пучка, прошедшего среду и преобразованное оптической системой указанным образом, также несет в себе информацию о неоднородностях показателя преломления, наведенных в среде при прохождении световой волны, и может быть использовано для расчета коэффициента нелинейности показателя преломления. При этом обнаружено, что при наблюдении распределения интенсивности преобразованного таким образом излучения отсутствует эффект сильного и статистически неустойчивого изменения пространственного распределения интенсивности излучения при небольших случайных изменениях мощности падающего пучка. Обнаружено также, что эффект перераспределения интенсивности в пучке после его преобразования по сравнению с исходным распределением проявляется ярко уже при относительно небольших мощностях падающего излучения, далеких от порога разрушения, на эффект не накладывает ограничений длительность воздействия падающего излучения. При этом образец измеряемой среды может быть в любом агрегатном состоянии, а его длина должна быть такова, чтобы его можно было считать оптически тонким, т.е. при распространении излучения внутри образца не происходило бы существенного перераспределения электромагнитного поля за счет нелинейных эффектов и дифракции света. В частности, для наиболее распространенных стекол образец может иметь длину от нескольких сантиметров до одного-двух дециметров при условии, что волновой фронт падающего излучения не сильно отличается от плоского. Поперечные размеры образца выбираются такими, чтобы исключить влияние стенок на картину взаимодействия световой волны, т.е. он должен быть существенно больше диаметра пучка. Способ может быть реализован для любого вида распределения интенсивности падающего пучка, однако особенности наблюдаемого изображения таковы, что наиболее точное определение нелинейной части показателя преломления обеспечивается при использовании пучков с распределением интенсивности типа Эйри, “гауссова”, “супергауссова”, для которых максимальная интенсивность в изображении пучка, прошедшего среду и преобразованное оптической системой указанным образом, слабее всего (по сравнению с другими типами распределений), зависит от мощности падающего на среду излучения и определяется, при прочих равных условиях эксперимента, величиной коэффициента нелинейности показателя преломления.

Моменты измерений распределений интенсивности падающего и прошедшего среду пучков отделены временным промежутком, в течение которого излучение проходит расстояние от плоскости падения пучка на среду до плоскости, в которой осуществляется измерение распределения интенсивности прошедшего среду пучка.

Распределения интенсивности в плоскости падения излучения на среду и в плоскости, расположенной за тестируемой средой по ходу луча, но оптически сопряженной с плоскостью, находящейся до среды, связаны между собой уравнением, получающимся в результате преобразования Френеля, описывающего распространение световой волны, с учетом параметров оптической схемы измерений. В общем виде для пространственно-временного распределения интенсивности пучка, прошедшего среду, при произвольном распределении интенсивности и фазы падающего на среду пучка, уравнение записывается в виде:

где

I· (x₁,y₁,t), I(x₂,y₂,t) - пространственно-временное распределение интенсивности излучения падающего и прошедшего среду, соответственно;

x₁,y₁ и х₂,у₂ - пространственные координаты в плоскости падения и плоскости, находящейся перед оптической средой, которая оптически сопряжена с плоскостью регистрации распределения интенсивности прошедшего среду пучка соответственно;

t - время;

- комплексная амплитуда поля, падающего на среду лазерного пучка;

ϕ (x₁,y₁) - распределение фазы в падающем на среду пучке;

λ - длина волны излучения;

L₁ - расстояние от плоскости падения пучка на среду до передней главной плоскости оптической системы;

L₂ - расстояние от задней главной плоскости оптической системы до плоскости регистрации распределения интенсивности прошедшего среду пучка;

Ф - оптическая сила оптической системы, причем выполняются соотношения Ф=1/L+1/L₂ и L>L₁. Первое из этих соотношений является условием передачи изображения оптической системой, второе определяет место проецируемой плоскости впереди среды;

L - расстояние от плоскости, находящейся перед средой, с которой оптически сопрягается плоскость регистрации распределения интенсивности прошедшего среду пучка, до передней главной плоскости преобразующей пучок оптической системы;

n₂ - коэффициент нелинейности показателя преломления;

L_S - длина образца оптической среды.

Коэффициент нелинейности показателя преломления вычисляется путем решения уравнения (1) численным методом.

Для регистрации пространственно-временного распределения интенсивности пучка можно использовать как измерительную аппаратуру, регистрирующую интегральные характеристики пучка за время импульса облучения при одновременной регистрации формы импульса, так и высокоскоростную аппаратуру, регистрирующую "мгновенные" распределения интенсивности пучка и временное распределение мощности. Тогда в первом случае можно использовать, например, видеокамеру, калориметр, осциллограф, а во втором в качестве фотоприемника может быть использован скоростной фотоэлектронный регистратор с пикосекундным разрешением во времени и измеритель мощности.

При этом величина I(x₁,y₁,t) определяется для первого и второго случаев из соотношений (2) и (3), соответственно:

где E - энергия импульса лазерного излучения;

F(x₁,y₁) - распределение градаций “серого” в изображении пучка, падающего на исследуемую среду, полученное на фотоприемнике;

θ _S(t) - описывает временную зависимость мощности излучения в образце;

θ (t) - форма импульса излучения, зарегистрированная осциллографом;

P(t) - временная зависимость мощности;

S - площадь изображения падающего на среду пучка, по которой осуществляется интегрирование.

Подобным же образом определяют и величину I(х₁,у₁,t).

Вся совокупность признаков заявляемого способа измерения позволяет достичь указанного выше технического результата.

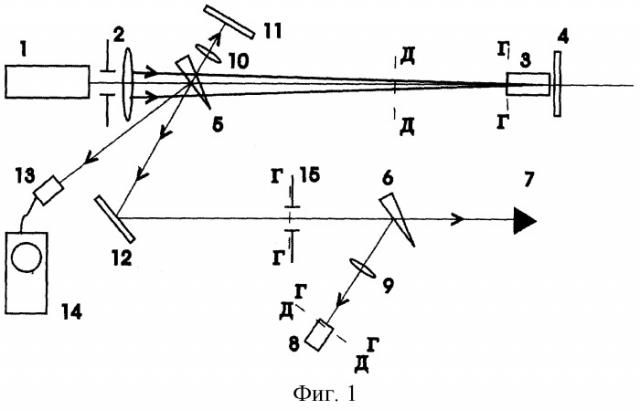
На фиг.1 приведена оптическая схема установки для измерения коэффициента нелинейности показателя преломления, где 1 - лазер; 2 - оптическая система; формирующая в плоскости падения пучка на среду некоторое распределение интенсивности и фазы; 3 - измеряемая оптическая среда; 4, 11, 12 - зеркала; 5, 6 - клинья; 7 - калориметр; 8 - фотоприемник; 9, 10 - объективы; 13 - фотоэлемент; 14 - осциллограф; 15 - диафрагма, Г-Г - плоскость падения пучка на среду и оптически сопряженные с ней плоскости диафрагмы 15 и видеокамеры 8, Д-Д - плоскость, находящаяся за средой по ходу пучка, оптически сопряженная с плоскостью, расположенной перед средой.

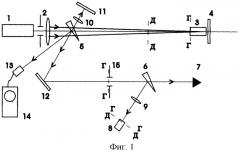
На фиг.2 приведен пример зарегистрированных видеокамерой изображений падающего и прошедшего среду пучков, реализованных в примере конкретного выполнения, (А) и графики распределения плотности энергии в поперечном сечении пучка, полученные для образца из стекла ГЛС-22 при плотности энергии на оси падающего пучка 9,2 Дж/см² (Б и В). Б - график распределения плотности энергии в поперечном сечении пучка в плоскости падения пучка на среду, В - график распределения плотности энергии в поперечном сечении прошедшего среду пучка в плоскости, оптически сопряженной с плоскостью, находящейся на расстоянии 150 см перед измеряемой оптической средой.

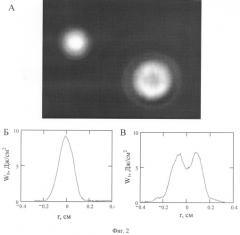
На фиг.3 представлены расчетные зависимости осевой плотности энергии W₁(0) в прошедшем нелинейную среду пучке от осевой плотности пучка, падающего на среду W₀(0), для плавленого кварца КУ2 для n₂=0,97· 10^-12 м³/Дж (сплошная линия) и лазерного стекла ГЛС 22 для n₂=2,1· 10^-12 м³/Дж (пунктирная линия). Крестики (для КУ-2) и квадраты (для стекла ГЛС-22) - экспериментально измеренные значения.

Заявленный способ был экспериментально осуществлен для измерения коэффициента нелинейности показателя преломления плавленого кварца КУ-2 и лазерной активной среды - стекла ГЛС-22. Для этого была создана экспериментальная установка, оптическая схема которой представлена на фиг.1.

Лазер 1 генерирует моноимпульс с длительностью τ =3.6 нс по полувысоте и энергией до 1 Дж. Длина волны излучения 1,06 мкм. Оптическая система 2 на выходе лазера формирует в плоскости падения пучка на исследуемую среду 3 (плоскопараллельная пластина длиной 10 см) пучок с плоским волновым фронтом и Эйри-распределением интенсивности с диаметром первого темного кольца 3,4 мм. Для усиления эффекта самовоздействия вплотную к образцу размещалось зеркало 4, отражающее 100% излучения в обратном направлении. Достижение указанного выше технического результата возможно и без применения зеркала 4, т.е. в схеме “на один проход”. Мы использовали зеркало для дополнительного усиления эффекта самовоздействия. Клинья 5 и 6 отводят часть излучения в калориметр 7 и видеокамеру 8, использованную в нашем случае в качестве фотоприемника, регистрирующую в требуемом масштабе изображение пучка в плоскости, оптически сопряженной с плоскостью Г-Г падения пучка на среду 3, с помощью объектива 9. Наряду с этим изображением, характеризующим пространственное распределение интенсивности пучка в плоскости падения излучения на среду, видеокамера регистрирует пространственное распределение интенсивности в поперечном сечении прошедшего среду пучка в плоскости, оптически сопряженной с плоскостью Д-Д, находящейся на расстоянии 150 см перед измеряемой оптической средой.

Преобразование пучка осуществляется объективами 9, 10 и зеркалами 11, 12. Таким образом, в каждой вспышке лазера видеокамера в одном кадре записывает два изображения пучка - одно характеризует падающий на среду пучок, второе - пучок, прошедший через среду и затем преобразованный введенной в схему оптической системой 9, 10, 11, 12. Для измерения временных характеристик импульса излучения использовались показанные на схеме фотоэлемент 13 (ФЭК-20) и осциллограф 14 (С7-19). Диафрагма 15 расположена в плоскости, сопряженной с плоскостью падения пучка на среду Г-Г, и ее изображение также проецируется объективом 9 на фотоприемник. В нашем случае регистрировались интегральные характеристики: видеокамера фиксировала интегральное распределение градаций “серого” (“яркости”) изображения, пропорциональное распределению интенсивности за все время импульса облучения, а калориметр - полную энергию импульса, временное распределение регистрировалось с помощью осциллографа.

Для того, чтобы избежать влияния нестабильности работы лазерной системы, измерения входящих в формулу величин для падающего и прошедшего среду пучков осуществлялись в одном импульсе излучения. При этом видеокамера фиксирует изображения падающего и прошедшего среду пучков в одном кадре, длительность экспозиции которого превышает длительность импульса.

В описываемом примере конкретного выполнения исследуемая среда размещалась в каустике длиннофокусной (F=20 м) линзы, где волновой фронт падающего пучка является плоским, соответственно, в этом случае распределение фазы определяется как ϕ (х₁,у₁)=0 и множитель в уравнении для фазы

Регистрация распределения интенсивности прошедшего среду пучка осуществлялась видеокамерой, расположенной за средой по ходу излучения, при этом введенная в пучок оптическая система строила изображение плоскости, расположенной перед средой, в плоскости размещения видеокамеры.

На фиг.2 приведен кадр с зарегистрированными видеокамерой изображениями падающего (слева) и прошедшего (справа) среду пучка, (А) и графики распределения плотности энергии в поперечном сечении пучка, полученные для образца из стекла ГЛС-22 при плотности энергии на оси падающего пучка 9,2 Дж/см² (Б и В). Б - график распределения плотности энергии в поперечном сечении пучка в плоскости падения пучка на среду, В - график распределения плотности энергии в поперечном сечении прошедшего среду пучка в плоскости, оптически сопряженной с плоскостью, находящейся на расстоянии 150 см перед измеряемой оптической средой.

Из сравнения полученных распределений (Б) и (В) расчетным путем с учетом параметров формирующей оптической системы был определен коэффициент нелинейности показателя преломления для стекла ГЛС-22 n₂=(2,1±0.13)· 10^-12м³/Дж. Из аналогичным образом проведенных экспериментов было получено значение n₂=(0,97±0.1)· 10^-12 м³/Дж для плавленого кварца. Сравнение с известными из литературы данными измерений показывают, что результат получен с большой точностью. Метод прост и удобен в реализации, не требует для своего осуществления дорогостоящей аппаратуры, может быть использован для измерения коэффициента нелинейности показателя преломления в широком диапазоне длительностей воздействия излучения на среду и для сред в любом агрегатном состоянии. Для измерений требуется сравнительно небольшая (1-2 ГВт) мощность излучения, что предохраняет среду от разрушения.

Дополнительно заявляемый способ был реализован для случая, когда падающий пучок осесимметричен и регистрируется интегральная картина распределения градаций “серого” за время импульса излучения, а для вычисления коэффициента нелинейности П2 используются значения осевой плотности энергии пучка W(0). В этом случае уравнение, лежащее в основе расчетов, существенно упрощается и принимает вид:

где ƒ (r,t) - комплексная амплитуда поля осесимметричного лазерного пучка в плоскости падения на среду;

I(r,t) - интенсивность излучения в плоскости падения на среду;

r - поперечный радиус-вектор.

Прочие параметры, входящие в уравнение, те же, что и в уравнении (1). Оптическая схема эксперимента аналогична приведенной на фиг.1, оптическая система, преобразующая прошедший среду пучок, имела те же параметры, что и в предыдущем примере конкретного выполнения. Полученные результаты проиллюстрированы фиг.3, где представлены расчетные зависимости осевой плотности энергии в возмущенном нелинейной средой пучке от осевой плотности пучка, падающего на образец, для двух сред - плавленого кварца КУ2 (сплошная линия) и лазерного стекла ГЛС-22 (пунктирная линия). Там же нанесены экспериментально полученные точки (Х - для КУ-2, □ - для стекла ГЛС-22), на основе которых и были вычислены значения n₂, использованные для построения расчетных зависимостей. Из чертежа видно, что наблюдается очень хорошее совпадение расчетных значений и экспериментально полученных точек. По сравнению с описанными выше аналогами и прототипом результат получен с большей точностью.

Способ определения коэффициента нелинейности показателя преломления оптических сред, включающий направление на оптическую среду пучка лазерного излучения, определение коэффициента нелинейности показателя преломления, отличающийся тем, что регистрируют пространственно-временное распределение интенсивности и определяют распределение фазы падающего излучения в плоскости, перпендикулярной направлению распространения излучения и являющейся плоскостью падения пучка на среду, регистрируют пространственно-временное распределение интенсивности излучения, прошедшего среду, в плоскости, расположенной за средой по ходу пучка и оптически сопряженной с плоскостью пространства, перпендикулярной направлению распространения излучения и расположенной перед оптической средой, определение коэффициента нелинейности показателя преломления осуществляют расчетным путем из сравнения полученных распределений для падающего и прошедшего среду пучков.