Способ отождествления пеленгов источников радиоизлучений в угломерных двухпозиционных пассивных радиолокационных системах

Способ отождествления пеленгов источников радиоизлучений в угломерных двухпозиционных пассивных радиолокационных системах

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к радиолокационным системам, в частности к угломерным двухпозиционным пассивным радиолокационным системам (УДПРЛС).

В радиолокации весьма обширный и важный класс лоцируемых объектов составляют источники радиоизлучений (ИРИ), наблюдение за которыми осуществляется по принятым на приемных позициях (ПП) излученным ими радиосигналам. Широкое применение на практике нашли УДПРЛС, базирующиеся на пеленгационных методах [Черняк B.C. Многопозиционная радиолокация. - М.: Радио и связь, 1993, стр.73-74, 392-396], [Радиоэлектронные системы: Основы построения и теория. Справочник. / Ширман Я.Д., Лосев Ю.И., Минервин Н.Н. и др. / Под ред. проф. Я.Д.Ширмана. - М.: ЗАО” Маквис”, 1998, стр.608]. Одной из основных задач, которую необходимо решать при радиолокационном наблюдении в УДПРЛС, является задача отождествления пеленгов ИРИ, измеренных в различных ПП [Радиоэлектронные системы: Основы построения и теория. Справочник. / Ширман Я.Д., Лосев Ю.И., Минервин Н.Н. и др. / Под ред. проф. Я.Д.Ширмана. - М.: ЗАО “Маквис”, 1998, стр.608], [Теоретические основы радиолокации под ред. проф. Ширмана Я.Д. - М.: Сов. радио, 1970, стр.494-495]. Указанная задача установления соответствия между сигналами, принятыми в различных позициях от одного и того же источника, особенно актуальна, когда в секторе обзора УДПРЛС имеется несколько ИРИ.

Известны способы отождествления пеленгов, рассмотренные в работе [Радиоэлектронные системы: Основы построения и теория. Справочник. / Ширман Я.Д., Лосев Ю.И., Минервин Н.Н. и др. / Под ред. проф. Я.Д.Ширмана. - М.: ЗАО “Маквис”, 1998, стр.608] и [Теоретические основы радиолокации под ред. проф. Ширмана Я.Д. - М.: Сов. радио, 1970, стр.494-495], заключающиеся в том, что измеренные в двух ПП пеленги (углы места и азимуты ИРИ) относят к одному и тому же ИРИ, если линии положения, построенные по значениям измеренных пеленгов, имеют только одну общую точку (малую окрестность) пересечения. Недостаток этих способов: значительные вычислительные ресурсы при большом числе ИРИ.

Известен также способ отождествления пеленгов ИРИ, основанный на проверке условия компланарности векторов, два из которых совпадают с соответствующими линиями визирования, соединяющими ИРИ и приемные позиции, а третий вектор совмещен с базой приемных позиций [Колесса А.Е. Оценивание координат совокупности объектов, наблюдаемых многопозиционной системой пеленгации // Радиотехника и электроника, 1987, т.32, №12, стр.25-37]. Здесь и далее под базой понимается расстояние между приемными позициями. Этот способ также характеризуется большой сложностью при вычислениях, связанных с процедурой отождествления пеленгов.

Инвариантно-групповой способ отождествления пеленгов, рассмотренный в работе [Булычев Ю.Г., Таран В.Н. Инвариантно-групповой метод отождествления пеленгов цели в триангуляционных многопозиционных системах пассивной локации // Радиотехника и электроника, 1987, т.32, №4, стр.756-757], является наиболее близким аналогом (прототипом) заявленного изобретения. Он позволяет минимизировать вычислительные и аппаратурные затраты по сравнению с упомянутыми выше способами. Данный способ предполагает использование инвариантов, т.е. некоторых функций f(α , β , t) (где α , β - азимут и угол места ИРИ, см. фиг.1), значения которых остаются неизменными при подстановке в них значений пеленгов (то есть азимутов и углов места) ИРИ, полученных с различных точек визирования и лежащих на одной прямой. Для любого другого ИРИ указанные функции принимают иные значения. В качестве инварианта в прототипе используется тангенс угла (см. фиг.2, угол Θ ) между плоскостью, проходящей через ИРИ и базу угломерной системы (см. фиг.2, плоскость ПП₁ПП₂-ИРИ) и горизонтальной плоскостью (см. фиг.2, плоскость XOZ). Суть способа сводится к тому, что в некоторый момент времени в каждой i-ой приемной позиции для каждого j-ого ИРИ определяется значение инварианта f_i(α _j, β _j, t) и далее находится разность значений этих инвариантов, вычисленных для различных приемных позиций. Если эта разность меньше заданного порога отождествления, то пеленги считаются истинными, в противном случае - ложными.

Основной недостаток прототипа заключается в том, что в случае нахождения нескольких ИРИ в одной плоскости отождествление пеленгов этих ИРИ становится невозможным, поскольку для указанного способа отождествления плоскости пеленгации разных ИРИ совпадать не могут [Булычев Ю.Г., Коротун А.А. Применение совокупности инвариантов для решения задачи отождествления пеленгов в угломерных системах // Радиотехника и электроника, 1989, т.34, №1, стр.97]. Под плоскостью пеленгации здесь и далее понимается плоскость, проходящая через ИРИ и приемные позиции (см. фиг.2, плоскость -ПП₁ПП₂-ИРИ₁).

Таким образом, задачей изобретения является отождествление пеленгов нескольких ИРИ даже в случае нахождения их в одной плоскости и, тем самым, расширение возможности пассивного радиолокационного способа наблюдения ИРИ.

Для облегчения понимания средств достижения поставленной задачи поясним физические принципы, положенные в основу заявляемого способа. Решение задачи базируется на двух геометрических положениях:

- во-первых, один и тот же ИРИ не может не находиться на линии (см. фиг.1, линия ИРИ_г-ИРИ) пересечения двух вертикальных плоскостей, каждая из которых проходит через одну из приемных позиций и соответствующую этой позиции линию визирования ИРИ (см. фиг.2, плоскости ПП₁-ИРИ_г-ИРИ и ПП₂-ИРИ_г-ИРИ);

- во-вторых, на этой линии имеется единственная точка (см. фиг.1, точка ИРИ), в которой пересекаются линии визирования, соединяющие данный ИРИ с каждой из приемных позиций (см. фиг.2, линии ПП₁-ИРИ и ПП₂-ИРИ).

Отсюда следуют два вывода:

1) если две ПП находятся в одной горизонтальной плоскости, то измеренные или оцененные в каждой из них значения высоты ИРИ (см. фиг.1 и 2, линия h) должны быть равны, т.е. h₁=h₂, где h₁ - значение высоты h ИРИ, измеренное первой приемной позицией, h₂ - значение высоты h ИРИ, измеренное второй ПП;

2) если две ПП находятся не в одной горизонтальной плоскости, то расстояние между горизонтальными плоскостями, в которых находятся эти ПП, равно разности оцененных значений высот ИРИ, рассчитанных в двух ПП.

Следовательно, высоту ИРИ h можно считать инвариантом.

Таким образом, для отождествления пеленгов ИРИ в УДПРЛС необходимо: по измеренным, в каждой из двух приемных позициях, значениям пеленгов ИРИ найти значение высоты ИРИ относительно высоты каждой из приемных позиций; оценить разность этих высот; определить значение порога отождествления и сравнить разность высот ИРИ с этим порогом, по результатам сравнения принять решение об отождествлении пеленга ИРИ.

Итак, заявленный способ отождествления пеленгов ИРИ в УДПРЛС осуществляют следующим образом:

- в первой приемной позиции (ПП₁) измеряют значения азимута α _i и угла места β _i каждого i-гo здесь и в дальнейшем черта в формуле над текстом указывает, что значения переменной изменяются от 1 до максимального значения, в данном случае до I, с шагом 1) из всех I ИРИ, а также значения собственных координат x₁, z₁ и y₁ в земной прямоугольной системе координат;

- передают измеренные значения азимутов α _i, углов места β _i всех обнаруженных ИРИ и собственных координат x₁, z₁, y₁ во вторую приемную позицию (ПП₂);

- во второй приемной позиции измеряют значения собственных координат x₂, z₂, у₂ в той же системе координат, а также значения азимута α _j и угла места β _j каждого j-гo из всех J (J=I) ИРИ, причем во второй приемной позиции:

- определяют значение базы d - расстояния между ПП₁ и ПП₂ по формуле

где x₁, z₁, y₁ и x₂, z₂, у₂ - координаты ПП₁ и ПП₂, соответственно, в земной прямоугольной системе координат;

- вычисляют высоту h_i i-гo ИРИ по отношению к высоте первой приемной позиции:

где α _i, α _j - измеренные значения азимута i-гo ИРИ в ПП₁ и j-го ИРИ в ПП₂, соответственно;

β _i и β _j - измеренные значения угла места i-гo ИРИ в ПП₁ и j-го ИРИ в ПП₂, соответственно;

- вычисляют высоту h_j j-го ИРИ по отношению к высоте второй приемной позиции

- вычисляют значение Δ h_ij - модуля разности высот ИРИ

где | ... | - знак математической операции нахождения модуля числа;

- определяют значение - дисперсии ошибки вычисления модуля разности высот ИРИ Δ h_ij по формуле

где kα _i, kα _j, kβ _i и kβ _j - весовые коэффициенты, значения которых находят по формулам:

а , и , - дисперсии ошибок измерения азимута и угла места в ПП₁ и ПП₂, соответственно;

- находят порог отождествления ε _ij по формуле

где μ - постоянный коэффициент, зависящий от заданной вероятности правильного отождествления пеленгов;

- принимают решение об отождествлении пеленгов ИРИ по правилу:

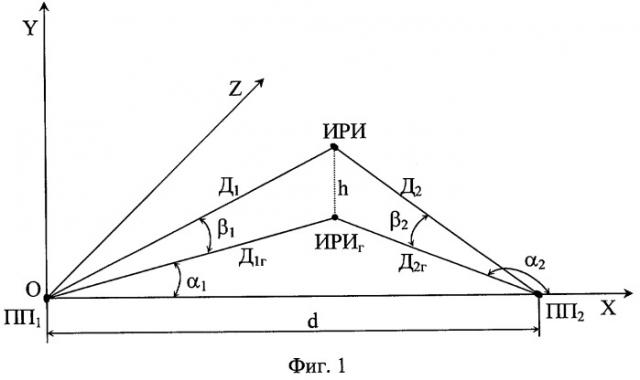
Фиг.1 и 2 поясняют геометрию решения задачи отождествления пеленгов на основе инвариантности высоты ИРИ.

На фиг.1 обозначено:

OYXZ - прямоугольная система координат с началом, совмещенным с первой приемной позицией, ось ОХ проходит через вторую приемную позицию, оси OY и OZ - перпендикулярны оси ОХ и образуют правую прямоугольную систему координат, в которой плоскость ZOX - горизонтальная плоскость;

ИРИ, ИРИ_г - источник радиоизлучения и его проекция на горизонтальную плоскость, соответственно;

α ₁ и β ₁ - азимут и угол места ИРИ, измеренные угломером первой приемной позиции;

α ₂ и β ₂ - азимут и угол места ИРИ, измеренные угломером ПП₂;

h - высота ИРИ;

Д₁, Д_{1 г} - дальность от ПП₁ до ИРИ и ее проекция на горизонтальную плоскость, соответственно;

Д₂, Д_{2 г} - дальность от ПП₂ до ИРИ и ее проекция на горизонтальную плоскость, соответственно;

d - база.

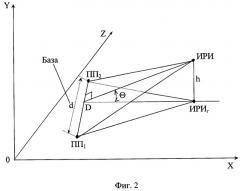
На фиг.2 обозначено:

OYXZ - прямоугольная система координат;

ИРИ, ИРИ_г - источник радиоизлучения и его проекция на горизонтальную плоскость, соответственно;

h - высота ИРИ;

ПП₁, ПП₂ - местоположения первой и второй приемных позиций;

линия ИРИ-D - перпендикуляр, опущенный из точки ИРИ на базу d;

Θ - угол между плоскостями ПП₁-ПП₂-ИРИ и ПП₁-ПП₂-ИРИ_г.

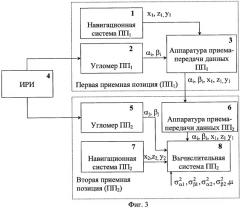
На фиг.3 представлена упрощенная структурная схема УДПРЛС, в котором может быть реализован заявленный способ отождествления пеленгов ИРИ, где:

1 - навигационная система ПП₁;

2 - угломер ПП₁;

3 - аппаратура приема-передачи данных ПП₁;

4 - источники радиоизлучений;

5 - угломер ПП₂;

6 - аппаратура приема-передачи данных ПП₂;

7 - навигационная система ПП₂;

8 - вычислительная система ПП₂.

В Приложении приведены пояснения к некоторым используемым в заявленном способе формулам.

Рассмотрим функционирование УДПРЛС при использовании заявленного способа отождествления пеленгов ПРИ.

В состав УДПРЛС входят первая и вторая приемные позиции, которые могут быть стационарными либо подвижными. Первая приемная позиция (ПП₁) содержит: навигационную систему 1; угломер 2 (называемый часто в литературе пеленгатором); аппаратуру приемо-передачи данных 3. Вторая приемная позиция (ПП₂) содержит: угломер 5; аппаратуру приемо-передачи данных 6; навигационную систему 7; вычислительную систему 8. Принципы функционирования этих устройств подробно описаны в научно-технической литературе [Черняк B.C. Многопозиционная радиолокация. - М.: Радио и связь, 1993, стр.73-74, 392-396; Радиоэлектронные системы: Основы построения и теория. Справочник / Ширман Я.Д., Лосев Ю.И., Минервин Н.Н. и др. / Под ред. проф. Я.Д.Ширмана. - М.: ЗАО “Маквис”, 1998, стр.608; Теоретические основы радиолокации под ред. проф. Ширмана Я.Д. - М.: Сов. радио, 1970, стр.494-495]. К принципам их построения и функционирования заявляемый способ не предъявляет никаких дополнительных требований, поэтому ниже, при описании функционирования УДПРЛС, используется общая характеристика данных устройств.

После включения УДПРЛС в вычислительную систему 8 ПП₂ вводят значения и - дисперсий ошибок измерения азимутов и углов места угломером 2 ПП₁ и угломером 5 ПП₂, соответственно, а также значение постоянного коэффициента μ .

Источники радиоизлучения 4, количество которых может быть от 1 до I, излучают радиосигналы, принимаемые угломером 2 ПП₁ и угломером 5 ПП₂.

Угломер 2 ПП₁ по принятым радиосигналам измеряет значения пеленгов ИРИ, то есть значения азимута α _i угла места каждого i-го из всех I ИРИ, и передает их в аппаратуру приемо-передачи данных 3 ПП₁.

Угломер 5 ПП₂ по принятым радиосигналам также измеряет значения пеленгов этих ИРИ, то есть значения азимута α _j и угла места каждого j-го из всех J (J=I) ИРИ, и передает их в вычислительную систему 8 ПП₂. В силу того, что в каждой приемной позиции ведется своя независимая нумерация источников радиоизлучения, то ИРИ в каждой из них обозначаются соответственно индексами - i и j.

Навигационная система 1 ПП₁ определяет местоположение первой приемной позиции в земной прямоугольной системе координат в виде значений x₁, z₁, y₁ и передает их в аппаратуру приемо-передачи данных 3 ПП₁.

Навигационная система 7 ПП₂ определяет местоположение второй приемной позиции в той же системе координат в виде значений x₂, z₂, y₂ и передает их в вычислительную систему 8 ПП₂.

С помощью аппаратуры приемо-передачи данных 3 ПП₁ измеренные значения азимутов α _i, углов места β _i всех I ИРИ, а также значения координат ПП₁ x₁, z₁, y₁ передают в аппаратуру приема-передачи данных 6 ПП₂, которая их принимает и передает далее в вычислительную систему 8 ПП₂.

Вычислительная система 8 ПП₂, используя полученные значения пеленгов ИРИ и значения координат ПП₁ и ПП₂, выполняет следующее:

- по формуле (1) вычисляет значение базы d между ПП₁ и ПП₂;

- по формуле (2) вычисляет значение высоты h₁ каждого i-го ИРИ по отношению к плоскости, проходящей через базу d и i-ым ИРИ;

- по формуле (3) вычисляет значение высоты h_j каждого j-го ИРИ по отношению к плоскости, проходящей через базу d и j-ым ИРИ;

- по формуле (4) для каждой пары высот h_i и h_j вычисляет значение Δ h_ij - модуля разности высот ИРИ;

- по формулам (6)-(9) для каждого модуля разности высот ИРИ Δ h_ij вычисляет значения весовых коэффициентов

- по формуле (5) для каждого модуля разности высот ИРИ Δ h_ij вычисляет - значение дисперсии ошибки вычисления модуля разности высот;

- по формуле (10) для каждого модуля разности высот ИРИ Δ h_ij вычисляет порог отождествления ε _ij;

- принимает решение об отождествлении пеленгов ИРИ по правилу (11).

К принципам построения и алгоритмам функционирования навигационных систем, угломеров, аппаратуры передачи данных и вычислительной системы заявленный способ не предъявляет никаких особых требований: в качестве указанных устройств могут быть использованы любые из существующих в настоящее время. Все это подтверждает практическую применимость заявленного способа.

Заявленный способ отождествления пеленгов ИРИ, базирующийся на инвариантности высоты ИРИ, расширяет возможности локационного наблюдения ИРИ в пространстве.

Кроме того, использование в заявленном способе адаптивного порога отождествления позволяет автоматически учесть влияние на точность определения пеленгов местоопределения ИРИ относительно ПП, что значительно повышает вероятность правильного отождествления пеленгов ИРИ.

Приложение

Ряд пояснений к используемым в заявленном способе формулам

1. Формула (2) получена из треугольника ПП₁-ИРИ-ИРИ_г (см. фиг.1), в котором

где β ₁ - угол места ИРИ, измеренный из ПП₁, h - высота ИРИ, а Д_{1 г} - проекция дальности Д₁ на горизонтальную плоскость, рассчитываемая по формуле

где α ₁, α ₂ - азимуты ИРИ, измеренные в первой и второй ПП, соответственно.

2. Формула (3) получена из треугольника ПП₂-ИРИ-ИРИ_г (см. фиг.1), в котором

где β ₂ - угол места ИРИ, измеренный из ПП₂, а Д_{2 г} - проекция дальности Д₂ на горизонтальную плоскость, рассчитываемая по формуле

3. Из чертежа (см. фиг.1) и формул (2) и (3) следует, что значение высоты h ИРИ, вычисляемое по формуле (2), в общем случае не будет совпадать с его значением, вычисленным по формуле (3), поскольку при вычислении этих значений высот используются углы β ₁, β ₂, α ₁, α ₂, значения ошибок измерения Δ α ₁, Δ α ₂, Δ β ₁ и Δ β ₂ которых в основном предопределяются местоположением ИРИ относительно ПП₁ и ПП₂. Поэтому в основе предлагаемого способа отождествления лежит использование вычисляемого для каждого ИРИ порога отождествления ε _ij, значение которого зависит от значения - дисперсии ошибки вычисления модуля разности высот ИРИ Δ h_ij (4).

При описанном способе измерений пеленгов ИРИ ошибки Δ α _i, Δ α _j, Δ β _i, и Δ β _j измерения углов α _i, α _j, β _i и β _j являются нормально распределенными случайными величинами с нулевыми математическими ожиданиями и соответствующими дисперсиями , , , и . Для высокоточных измерений случайную величину Δ h_ij=|h₁-h_j| - модуль разности высот ИРИ - также можно считать распределенной по нормальному закону. Линеаризация случайной величины Δ h_ij в окрестности ее истинного значения, с учетом статистической независимости ошибок измерения углов α _i, α _j, β _i и β _j и пренебрежения ошибками измерения базы d позволяет получить выражение для нахождения дисперсии (5). В выражении (5) весовые коэффициенты kα _i, kα _j, kβ _i и kβ _j, описываемые соответственно формулами (6)-(9), были получены из следующих соотношений:

Поскольку для высокоточных измерений справедливо следующее известное соотношение [Справочник по радиолокации./Под ред. М.Сколника. Нью-Йорк, 1970. Пер. с англ. (в четырех томах) под общей ред. К.Н.Трофимова. Том 4. Радиолокационные станции и системы. - М.: Сов. Радио, 1978, стр.235]:

M{f(x)}≈ f(M{x}),

где f(x) -произвольная функция случайного аргумента, а математическое ожидание случайной величины М{х}=М{Δ h_ij}, то

Таким образом, случайная величина Δ h_ij распределена по нормальному закону, моменты которого определяются из формул (5) и (3П). Отличительной особенностью дисперсии является то, что ее нельзя вычислить заранее, поскольку она зависит от конкретного местоположения ИРИ относительно приемных позиций.

4. Порог отождествления ε _ij (10) однозначно связан с вероятностными характеристиками алгоритма отождествления пеленгов, которые, в свою очередь, определяются дисперсией . В частности, для истинных значений пеленгов ИРИ вероятность выполнения условия (11) (вероятность правильного отождествления) при фиксированном i можно охарактеризовать как вероятность попадания нормально распределенной случайной величины Δ h_ij в заданный интервал:

где: P(| Δ_hii | < ε_ii) - вероятность правильного отождествления пеленгов ИРИ; - функция Лапласа; - среднеквадратичное отклонение ошибки определения высоты одного и того же ИРИ разными ПП.

Из (4П) можно найти значение порога отождествления ε _ij, если задаться вероятностью правильного отождествления пеленгов. Однако значение порога отождествления ε _ij не может быть вычислено заранее, так как оно зависит не только от заданной вероятности правильного отождествления, но и неизвестной дисперсии которая определяется соотношением (5). Отсюда следует, что значение порога отождествления ε _ij должно рассчитываться после каждого цикла измерений по формуле (10), в которой μ - постоянный коэффициент, зависящий от заданной вероятности правильного отождествления пеленгов P(|Δ_hii | < ε) (4П). Например, при вероятности правильного отождествления близкий к единице коэффициент μ берется равным 3.

5. Пояснения к выражению (11).

Решение об отождествлении пеленгов ИРИ по правилу (11) основано на следующем.

Если азимут α _i и угол места β _i i-го ИРИ, измеренные в ПП₁, и азимут α _j и угол места β _j j-гo ИРИ, измеренные в ПП₂, относятся к одному и тому же ИРИ, то разность Δ h_ij будет меньше порога отождествления ε _ij.

Если азимут α _i и угол места β _i i-го ИРИ, измеренные в ПП₁, и азимут α _j и угол места β _j j-гo ИРИ, измеренные в ПП₂, относятся к разнесенным в пространстве ИРИ, то значение порога отождествления ε _ij, характеризующего суммарную ошибку определения оценок высот двух ИРИ, будет меньше, чем разность высот Δ h_ij этих ИРИ. В этом случае применение правила (11) приведет к принятию решения о том, что отождествляемые пеленги принадлежат разным ИРИ.

Для отождествления всех I пеленгов ИРИ, измеренных угломером первой ПП, необходимо последовательно каждый i-й пеленг, начиная с i=1 и заканчивая i=I, отождествить последовательно с каждым пеленгом, зафиксированным второй ПП, начиная c j=1 и заканчивая j=J.

Способ отождествления пеленгов источников радиоизлучений в угломерных двухпозиционных пассивных радиолокационных системах, заключающийся в том, что в первой приемной позиции (ПП₁) измеряют значения азимута α₁ и угла места β₁ каждого i-гo (, черта в формуле над текстом указывает, что значения переменной изменяются от 1 до максимального значения, в данном случае до I, с шагом 1) из всех I источников радиоизлучений (ИРИ), а также значения собственных координат x₁, z₁, y₁ в земной прямоугольной системе координат, передают измеренные значения азимутов α_i, углов места β_i всех обнаруженных ИРИ и собственных координат x₁, z₁, y₁ во вторую приемную позицию (ПП₂), во второй приемной позиции измеряют значения собственных координат х₂, z₂, y₂ в той же системе координат, а также значения азимута α_j и угла места β_j каждого j-гo () из всех J (J = I) ИРИ, отличающийся тем, что во второй приемной позиции определяют значение базы d - расстояния между ПП₁ и ПП₂ по формуле

где x₁, z₁, y₁ и x₂, z₂, y₂ - координаты ПП₁ и ПП₂, соответственно, в земной прямоугольной системе координат,

вычисляют высоту h_i i-гo ИРИ по отношению к высоте ПП₁ по формуле

где α_i, α_j - измеренное значение азимута i-гo ИРИ в ПП₁ и j-гo ИРИ в ПП₂, соответственно;

β₁ и β_j - измеренные значения угла места i-гo ИРИ в ПП₁ и j-гo ИРИ в ПП₂, соответственно,

вычисляют высоту h_j j-гo ИРИ по отношению к высоте ПП₂ по формуле

находят Δh_ij - значение модуля разности высот ИРИ по формуле

где |...| - знак математической операции нахождения модуля числа, определяют значение - дисперсии ошибки вычисления модуля разности высот ИРИ Δh_ij согласно выражению

где kα_i, kα_j, kβ_i и kβ_j - весовые коэффициенты, значения которых находят по формулам

a , и , - дисперсии ошибок измерения азимута и угла места первой и второй приемными позициями, соответственно, находят порог отождествления ε_ij по формуле

где μ - постоянный коэффициент, по правилу:

принимают решение об отождествлении пеленгов ИРИ.