Способ определения диэлектрических характеристик поликристаллических материалов, в частности ферритов

Способ определения диэлектрических характеристик поликристаллических материалов, в частности ферритов

Иллюстрации

Показать все

Реферат

Изобретение относится к области контрольно-измерительной техники и может быть использовано для определения диэлектрических характеристик ферритовых материалов при различных температурах в широком диапазоне частот измерительного сигнала.

Наиболее близким, принятым за прототип, является способ определения диэлектрических характеристик поликристаллических материалов, в частности, ферритов (Суржиков А.П., Пешев В.В., Гынгазов С.А. Известия ВУЗов. Физика. №10, 2000 г., с.49-52). Согласно способу на противоположные стороны плоского образца наносят тонкопленочные электроды так, чтобы один из них перекрывал площадь другого, проводят нормализующий отжиг, охлаждают образец до температуры не менее 77 К, постепенно нагревают образец до температуры 500-520 К, одновременно измеряют при различных значениях температуры на измерительном напряжении заданной частоты с амплитудой 200-300 мВ величины емкости образца С и полной проводимости G, определяют для различных значений температуры образца величины действительной ε ’ и мнимой ε ’’ частей диэлектрической проницаемости материала образца по формулам:

где tgδ - тангенс угла диэлектрических потерь;

ε ₀=8.85· 10^-12 Ф/м - диэлектрическая постоянная;

d - толщина образца;

s - площадь перекрытия электродов;

ω - частота измерительного сигнала,

строят графики температурных зависимостей ε ’, ε ’’ для заданной частоты измерительного сигнала, из графика для величины ε ’ по количеству участков, характеризующих увеличение ε ’ с увеличением температуры, определяют количество типов электрических диполей, преобладающих в образце, исходя из анализа температурных зависимостей ε ’ и ε ’’ определяют характеристические параметры для материала образца: величину статической диэлектрической проницаемости; значения предэкспоненциальных факторов, характеризующих постоянное время переориентации каждого типа диполей; значения величин, характеризующих перенос носителей заряда в электрическом поле, используя определенные таким образом значения характеристических параметров, из выражений, устанавливающих аналитическую связь величин ε ’, ε ’’, tgδ с характеристическими параметрами, частотой измерительного сигнала и температурой образца, определяют величины ε ’, ε ’’, tgδ для заданных температуры образца и частоты измерительного сигнала.

Недостатками способа являются невысокая точность определения величин ε ’, tgδ и ε ’’.

Задачей изобретения является повышение точности определения диэлектрических характеристик.

Решение данной задачи достигается за счет того, что способ определения диэлектрических характеристик поликристаллических материалов в частности, ферритов, так же, как в прототипе, включает в себя нанесение на противоположные стороны плоского образца тонкопленочных электродов так, чтобы один из них перекрывал площадь другого. Проводят нормализующий отжиг, охлаждают образец до температуры не менее 77 К, затем постепенно нагревают образец до температуры 500-520 К. Одновременно измеряют при различных значениях температуры на измерительном напряжении заданной частоты с амплитудой 200-300 мВ величины емкости образца С и полной проводимости G. Определяют для различных значений температуры образца величины действительной ε ’ и мнимой ε ’’ частей диэлектрической проницаемости материала образца по формулам:

где tgδ - тангенс угла диэлектрических потерь;

ε ₀=8.85· 10^-12 Ф/м - диэлектрическая постоянная;

d - толщина образца;

s - площадь перекрытия электродов;

ω - частота измерительного сигнала.

Затем строят графики температурных зависимостей ε ’, ε ’’ для заданной частоты измерительного сигнала, определяют из графика для величины ε ’ по количеству участков, характеризующих увеличение ε ’ с увеличением температуры, количество типов электрических диполей, преобладающих в образце. Определяют исходя из анализа температурных зависимостей ε ’ и ε ’’ характеристические параметры для материала образца: величину статической диэлектрической проницаемости; значения предэкспоненциальных факторов, характеризующих постоянное время переориентации каждого типа диполей; значения величин, характеризующих перенос носителей заряда в электрическом поле. Используя определенные таким образом значения характеристических параметров из выражений, устанавливающих аналитическую связь величин ε ’, ε ’’, tgδ с характеристическими параметрами, частотой измерительного сигнала и температурой образца определяют величины ε ’, ε ’’, tgδ для заданных температуры образца и частоты измерительного сигнала.

Согласно изобретению, после нанесения тонкопленочных электродов на противоположные стороны образца вокруг одного из электродов наносят охранный электрод, который при проведении электрических измерений заземляют, поверх тонкопленочных электродов наносят токопроводяшую пасту, во время нагрева образца измерение величин С и G проводят на трех - пяти фиксированных частотах измерительного сигнала, для каждой частоты измерительного сигнала проводят вышеуказанную последовательность действий по определению характеристических параметров материала, затем определяют средние значения этих параметров для совокупности значений частот измерительного сигнала, используя которые определяют величины ε ’, ε ’’, tgδ для произвольных температуры и частоты измерительного сигнала. Повышение точности определения величин ε ’, tgδ и ε ’’ достигается за счет: 1 - устранения поверхностных токов по поверхности образца от одного электрода к другому посредством их замыкания на землю через охранный электрод; 2 - выравнивания потенциала измерительного напряжения по поверхности тонкопленочных электродов вследствие увеличения их проводимости за счет токопроводящей пасты; 3 - более точного определения величин характеристических параметров материала вследствие их усреднения по количеству измерений на различных частотах измерительного напряжения.

Минимальное количество частот, на которых проводятся измерения температурных зависимостей проводимости и емкости образца, равно трем, так как при этом количестве достигается относительная погрешность в определении характеристических параметров не хуже 10%, что является достаточным условием для проведения корректной оценки величин ε ’, tgδ и ε ’’. Для количества частот менее трех относительная погрешность может достигать 30% и более. Для количества измерительных частот равному трем-пяти относительная погрешность лежит в пределах от 10% до 7%. Увеличение количества частот более пяти практически не изменяет погрешность в определении характеристических параметров. Поэтому оптимальным является интервал количества измерительных частот три - пять.

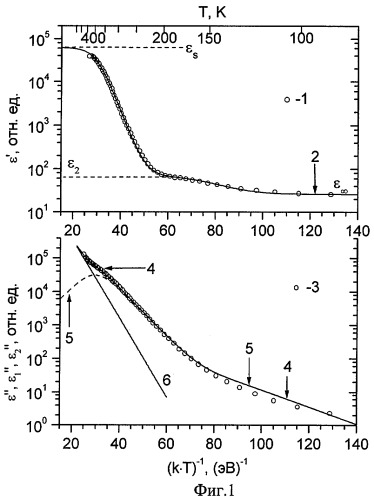
На фиг.1. представлены графики зависимостей электрофизических свойств Li-Ti феррита от температуры, полученные экспериментальным (кривые 1, 3), и расчетным путем (кривые 2, 4, 5, 6).

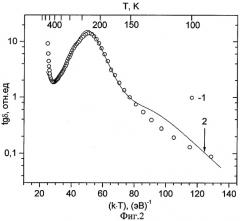
На фиг.2 представлены графики зависимости тангенса угла диэлектрических потерь от температуры, полученные экспериментальным (кривая 1) и расчетным путем (кривая 2).

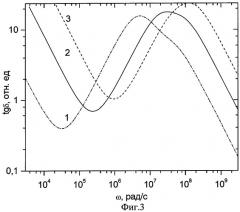
На фиг.3 представлены графики прогнозируемых частотных зависимостей тангенса угла диэлектрических потерь при различных температурах Т, К:1-223, 2-273, 3-323.

В таблице представлены значения характеристических параметров материала образца, определенные из анализа температурных зависимостей ε ’, ε ’’, полученных по результатам измерений величин С и G на различных частотах измерительного напряжения, и их средние значения по совокупности измерений.

Способ осуществляется следующим образом. Образец литий-титанового феррита, спеченный при температуре T=1370 К в течение времени t=4 ч имел форму таблетки диаметром 12.7 мм и толщиной 1 мм. Для получения однородного по объему состава таблетки окисленные слои с обеих сторон таблетки удалялись путем шлифования с последующей полировкой. Конечная толщина таблетки составляла d=0.32 мм. С обеих сторон таблетки методом термического испарения в вакууме были нанесены серебряные электроды толщиной 0.0015 мм. Диаметр одного электрода был равен 12 мм, диаметр второго электрода составлял 5 мм. Затем вокруг меньшего электрода на поверхность таблетки также методом термического испарения в вакууме был нанесен серебряный электрод толщиной 0.001 мм в виде кольца с внутренним диаметром 7 мм. Ширина кольца была 1 мм. Далее таблетка с контактами подвергалась нормализующему отжигу в печи МПЛ-6 при T=520 К в течение t=2 ч. Затем на поверхность измерительных электродов была нанесена путем намазывания кистью паста токопроводящая серебряная полимерная ПТСП-2 ЭПО.035.003 ТУ толщиной около 0.05 мм.

Отвердение пасты проводили в печи МПЛ-6 при температуре 478± 5 К в течение 25 мин на воздухе. После чего таблетка помещалась в терморегулирующую ячейку. К охранному электроду прижимался проволочный электрод, который заземлялся, а на оставшиеся два электрода подавалось через прижимные проволочные электроды измерительное напряжение с прибора Е7-12. Частота и напряжение измерительного сигнала были 1 МГц и 250 мВ, соответственно. Использовалась схема замещения: параллельное соединение конденсатора и сопротивления. Образец охлаждался до температуры 77 К с помощью жидкого азота. Путем прогрева терморегулирующей ячейки при подаче напряжения на нагревательный элемент, расположенный в корпусе ячейки, температура образца была постепенно увеличена до 500 К. Скорость нагрева регулировалась величиной напряжения, подаваемого на нагревательный элемент терморегулирующей ячейки, и составляла 0.5 град/мин. По мере нагрева образца проводились измерения его проводимости G и емкости С для различных значений температуры. По результатам измерений проводилось вычисление для различных значений температуры образца величин действительной ε ’ и мнимой ε ’’ частей диэлектрической проницаемости материала образца по формулам (1), (2), (3).

По вычисленным значениям построили графики температурных зависимостей ε ’, ε ’’ для заданной частоты измерительного сигнала. На фиг.1 представлены экспериментальные и расчетные температурные зависимости электрофизических параметров, измеренные на переменном напряжении. На графиках фиг.1 кривые: 1 и 2 - ε ’; 3 и 4 - ε ’’; 5 - ε ’’₁, слагаемое мнимой части комплексной диэлектрической проницаемости, обусловленное поляризационными токами, совпадающими по фазе с напряженностью поля; 6 - ε ’’₂, второе слагаемое, обусловленное проводимостью. При анализе этих зависимостей исходили из следующих соображений. С понижением температуры образца найдется такая температура T_L внутри вышеуказанного интервала, при которой переориентация диполей, имеющих минимальное значение характеристического времени τ этого процесса, будет "замороженной" и невозможной. Тогда значение ε ’(T_L) возможно равно или, по крайней мере, близко к значению ε_∞ . С повышением температуры найдется температура Т_H, при которой все виды диполей, даже с большим значением τ , будут успевать переориентироваться в фазе с электрическим полем. Тогда значение ε ’(T_H) возможно равно или, по крайней мере, близко к значению ε _s. Поэтому увеличение температуры (т.е. уменьшение 1/kT, где k - постоянная Больцмана), также как уменьшение частоты должны увеличивать число диполей, участвующих в процессе поляризации. Поэтому вид температурных зависимостей электрофизических параметров должен быть подобным виду их частотных зависимостей. Таким образом, электрофизические параметры диэлектрика определяют вид зависимостей ε ’(1/kT), ε ’’(1/kT) и, следовательно, из них можно получить значения этих параметров.

Из графика фиг.1 видно, что на экспериментально полученной зависимости действительной части диэлектрической проницаемости (кривая 1) с увеличением температуры наблюдаются две стадии увеличения ε ’. Это свидетельствует о наличии в образце двух типов диполей. В этом случае ε ’ описывается выражением, являющимся простой модификацией известной формулы (Богородицкий Н.П., Волокобинский Б.М., Воробьев А.А., Тареев Б.М. Теория диэлектриков. - Ленинград: Энергия, 1965, - 344 с., Уэрт Ч., Томсон Р. Физика твердого тела. М.: Мир, 1968, 560 с.):

где τ₁(x)=τ₁·exp(U₁·х) и τ₂(х)=τ₀₂·exp(U₂·х) - характеристические времена,

U₁ и U₂ - энергии активации переориентации релаксаторов первого и второго типов,

τ ₀₁ и τ ₀₂ - предэкспоненциальные факторы,

x=1/(k· T).

ε ₂ имеет смысл статической диэлектрической проницаемости при отсутствии диполей второго типа.

В общем случае выражение (4) - перепараметризовано (overparameterized), из-за чего невозможно использовать его для регрессионного анализа экспериментальных данных. Однако эту трудность можно избежать. Вначале для анализа использовалась низкотемпературная область на кривой 1, в которой поляризация, обусловленная вторым типом диполей, отсутствует (х≥ 62). В этом случае второе слагаемое в (4) отсутствовало. Использовались экспериментальные значения ε₂, ε_∞ (фиг.1).

В результате были найдены значения τ ₀₁ и U₁. Эти значения были занесены в таблицу.

Далее использовалась вся температурная область, и проводился анализ с использованием всего выражения (4), который дал значения ε _s, τ ₀₂ и U₂, которые были занесены в таблицу.

Из графика фиг.1 (кривая 3) видно, что образец обладает проводимостью, которая маскирует пики, связанные с наличием поляризационных токов. Вид этой кривой не исключает наличие переноса заряда с двумя значениями энергий активации. В этом случае мнимая часть описывается (Богородицкий Н.П., Волокобинский Б.М., Воробьев А.А., Тареев Б.М. Теория диэлектриков. - Ленинград: Энергия, 1965, - 344 с., Уэрт Ч., Томсон Р. Физика твердого тела. М.: Мир, 1968, 560с.):

где ε ’’₁, ε ’’₂ - слагаемые мнимой части диэлектрической проницаемости, первое из которых обусловлено поляризационными токами, совпадающими по фазе с напряженностью поля, второе - токами проводимости;

σ₁(х)=σ₀₁·ехр(-U_σ1·х) и σ₂(х)=σ₀₂·ехр(-U_σ2·х) - удельные электрические проводимости с энергиями активации U_σ1 и U_σ2;

σ ₀₁, σ ₀₂ - константы.

Оставались неоптимизированными параметры, характеризующие проводимость: σ₀₁,U_σ1 σ₀₂,U_σ2. Чтобы избежать перепараметризации выражения (5), для регрессионного анализа сначала использовали высокотемпературную область на кривой 3, постепенно расширяя ее до низких температур. При этом проводимость с меньшей энергией активации σ₁(х) отсутствовала в выражении (5). Анализ показал, что такой проводимости действительно нет и дал значения σ₀ и U_σ , которые приведены в таблице. С использованием значений величин, приведенных в таблице, были рассчитаны зависимости ε ''₁, ε ’’₂ (фиг.1) и tgδ (фиг.2).

Аналогичным образом были определены характеристические параметры для частот измерительного сигнала 100 Гц, 10 КГц и 100 КГц. Полученные значения характеристических параметров представлены в таблице. По совокупности числа измерительных частот были определены средние значения характеристических параметров, которые также представлены в таблице.

Далее был проведен расчет прогнозируемых частотных зависимостей tgδ (ω )=ε ’’(ω )/ε ’(ω ) путем подстановки определенных описанным выше способом средних значений характеристических параметров в выражения (4)-(7). Графики рассчитанных зависимостей для трех значений температуры Т: 1-223 К, 2-273 К, 3-323 К представлены на фиг.3. По этим зависимостям для данных температур были определены значения tgδ для частоты измерительного сигнала 1000 МГц, соответственно, 0,6; 2; 8, которые удовлетворительно совпали со значениями, определенными в заводских условиях для исследуемых образцов феррита. Таким образом, предлагаемый способ позволяет с высокой точностью определять диэлектрические характеристики материала.

Способ определения диэлектрических характеристик поликристаллических материалов в частности, ферритов.

Таблица
Электрофизические параметры Li-Ti феррита
Параметр	ε s, отн.ед	ε 2, отн. ед.	ε ∞ , отн.ед.	τ 01, с	τ 02, с
Значение на ω =1 МГц	6.3· 104	69	27	1.7· 10-9	1.37· 10-9
Значение на ω =100 Гц	6.1· 104	73	24	2.1· 10-9	1.13· 10-9
Значение на ω =10 КГц	6.4· 104	68	23	1.2· 10-9	1.36· 10-9
Значение на ω =100 КГц	6.0· 104	70	30	1.4· 10-9	1.66· 10-9
Среднее значение	6.2· 104	70	26	1.6· 10-9	1.38· 10-9
параметр	σ 0	Uσ , эВ	U1, эВ	U2, эВ
Значение на ω =1 МГц	4.3· 1013, с-1 СГСЕ	0.275	0.062	0.162
Значение на ω =100 Гц	3.9· 1013, с-1 СГСЕ	0.267	0.052	0.167
Значение на ω =1 КГц	4.1· 1013, с-1 СГСЕ	0.270	0.067	0.151
Значение на ω =100 КГц	4.5· 1013, с-1 СГСЕ	0.276	0.059	0.164
Среднее значение	4.2· 1013, с-1 СГСЕ	0.272	0.060	0.161

Способ определения диэлектрических характеристик поликристаллических материалов, в частности ферритов, заключающийся в том, что на противоположные стороны плоского образца наносят тонкопленочные электроды так, чтобы один из них перекрывал площадь другого, проводят нормализующий отжиг, охлаждают образец до температуры не менее 77 К, постепенно нагревают образец до температуры 500-520 К, одновременно измеряют при различных значениях температуры на измерительном напряжении заданной частоты с амплитудой 200-300 мВ величины емкости образца С и полной проводимости G, определяют для различных значений температуры образца величины действительной ε’ и мнимой ε’’ частей диэлектрической проницаемости материала образца по формулам:

где tgδ - тангенс угла диэлектрических потерь;

ε₀=8,85·10^-12 Ф/м - диэлектрическая постоянная;

d - толщина образца;

S - площадь перекрытия электродов;

ω - частота измерительного сигнала,

строят графики температурных зависимостей ε’, ε’’ для заданной частоты измерительного сигнала, из графика для величины ε’ по количеству участков, характеризующих увеличение ε’ с увеличением температуры, определяют количество типов электрических диполей, преобладающих в образце, исходя из анализа температурных зависимостей ε’ и ε’’ определяют характеристические параметры для материала образца: величину статической диэлектрической проницаемости; значения предэкспоненциальных факторов, характеризующих постоянное время переориентации каждого типа диполей; значения величин, характеризующих перенос носителей заряда в электрическом поле, используя определенные таким образом значения характеристических параметров, из выражений, устанавливающих аналитическую связь величин ε’, ε’’, tgδ с характеристическими параметрами, частотой измерительного сигнала и температурой образца, определяют величины ε’, ε’’, tgδ для заданных температуры образца и частоты измерительного сигнала, отличающийся тем, что на поверхность образца вокруг одного из электродов наносят охранный электрод, который при проведении электрических измерений заземляют, поверх тонкопленочных электродов наносят токопроводящую пасту, во время нагрева образца измерение величин С и G проводят на трех-пяти фиксированных частотах измерительного сигнала, для каждой частоты измерительного сигнала проводят вышеуказанную последовательность действий по определению характеристических параметров материала, затем определяют средние значения этих параметров для совокупности значений частот измерительного сигнала, используя которые определяют величины ε’, ε’’, tgδ для произвольных температуры образца и частоты измерительного сигнала.