Способ прогнозирования параметров землетрясения

Способ прогнозирования параметров землетрясения

Иллюстрации

Показать все

Реферат

Изобретение относится к сейсмологии и может найти применение при космическом мониторинге природных сред для прогнозирования землетрясений.

Множеством проведенных наблюдений в стадиях как до, так и после землетрясения, установлены корреляционные зависимости между сейсмической активностью в земной коре и интенсивностью электромагнитных процессов, проходящих в ионосфере и магнитосфере Земли. Исходя из общих физических принципов следует, что какой бы мощностью ни обладал источник возмущений, между двумя событиями - начальным и вновь установившимся состоянием - всегда существует переходный во времени процесс.

Измеряя характеристики переходного процесса (аномалии физических полей) до наступления природной катастрофы, можно рассчитать параметры ожидаемого удара: время, магнитуду, гипотетический центр очага. Аномалия, как правило, является результатом одновременного воздействия в некоторой области пространства разнородных физических факторов.

Известен способ обнаружения аномалий подстилающей поверхности (Патент RU №2.160.912, 2000 г. - аналог).

В способе-аналоге получают изображение подстилающей поверхности в виде цифровой функции яркости I(x,y) от пространственных координат, разбивают изображение на сравнительно однородные участки на основе априорных данных, вычисляют функции фрактальной размерности каждого участка, составляют матрицу эталонов из коэффициентов фрактальной размерности каждого участка, а аномалию фиксируют по выходу разности между текущими и эталонным значениями фрактальной размерности за пороговый уровень для анализируемого участка.

Недостатком способа-аналога являются:

- невозможность непосредственного использования для анализа физических полей природных сред;

- априорная неопределенность разбиения матрицы изображения на участки, искажающая числовые характеристики фрактальной размерности в пограничных областях.

Развитие космической техники предоставляет возможность непосредственного измерения физических полей, возникающих в околоземном космическом пространстве, путем соответствующего выбора высоты орбит космических систем и размещения на них регистрирующей аппаратуры. Ближайшим аналогом является способ предсказания землетрясений (Патент КП №2.205.430, 2003 г.).

В способе ближайшего аналога регистрируют волновой процесс, возникающий в ионосфере, в виде регистрограмм дискретных отсчетов электростатического потенциала внешней поверхности космических аппаратов при их полете по орбитам непосредственно через область ионосферного образования, фазовый центр волнового процесса находят как точку пересечения траверз восходящих и нисходящих витков космических аппаратов, проведенных к участкам регистрограмм, где доплеровская частота измеряемого процесса равна нулю, отождествляют эту точку с проекцией гипоцентра очага на ионосферу, вычисляют период Т₀, магнитуду М и время ожидаемого удара t_х из соотношений:

где Δ L=L₂-L₁ - разница между пространственными периодами двух симметричных относительно траверзы полуволн регистрограмм;

- отношение пространственных периодов двух симметричных относительно траверзы полуволн регистрограмм;

V - скорость акустических волн в ионосфере;

V_r - радиальная скорость движения измерителя относительно фазового центра волнового процесса;

d, l - коэффициенты регрессии;

dekr - натуральный логарифм отношений амплитуд сигнала двух смежных периодов.

Недостатками ближайшего аналога следует считать:

- математическая некорректность регрессионных зависимостей вычисления параметров землетрясения, в частности чем больше период Т₀, тем магнитуда М ожидаемого удара должна быть больше;

- неточность расчета параметров, связанная с визуально-графическим методом анализа регистрограмм;

- неопределенность значений V - скорости акустических волн в плазме и V_r - радиальной скорости движения носителя относительно фазового центра, непосредственно не измеряемые в способе, что снижает конечную точность прогноза.

Задача, решаемая заявляемым способом, состоит в повышении достоверности, статической устойчивости и точности определения прогнозируемых параметров землетрясения путем вычисления фрактальной размерности трехмерной матрицы, синтезируемой из регистрограмм нескольких физических полей (магнитного и электрического) околоземного космического пространства над очагом землетрясения и отслеживания динамики изменения фрактальной размерности по серии проходов измерителя (КА) над очаговой зоной.

Поставленная задача решается тем, что в способе прогнозирования параметров землетрясения, при котором получают регистрограммы дискретных отсчетов электромагнитных процессов на восходящем и нисходящем витках орбит КА, проходящих непосредственно через области физических полей, выделяют аномалии физических полей путем расчета фрактальной размерности их изображений и сравнения с эталонными значениями, определяют фазовый центр процесса и характеристики ожидаемого землетрясения по серии регистрограмм, дополнительно измеряют характеристики магнитного Н(x,y,z) и электрического Е(x,y,z) полей околоземного космического пространства раздельными датчиками в трех взаимно ортогональных плоскостях, формируют синтезированную матрицу из скалярных произведений векторов: R_i=Н_xiЕ_хi+Н_yiЕ_yi+Н_ziЕ_zi, вычисляют дисперсию сигнала по массиву R=R(R_i) измерений: и направляющие косинусы вектора переноса энергии:

рассчитывают фрактальную размерность D синтезированной матрицы и постоянную времени Т ее изменения из соотношения: прогнозируют время удара: t_y≅4,7Т, магнитуду М из соотношения как lg t_y[сут]=0,54М-3,37 и гипоцентр очага как точку пересечения векторов переноса энергии на восходящем и нисходящем витках,

где Δ t=t₂-t₁ - интервал времени между двумя измерениями для формирования синтезированных матриц;

D₁,D₂ - фрактальные размерности синтезированных матриц в моменты t₁, t₂;

D₀ - установившиеся значение фрактальной размерности накануне удара;

Изобретение поясняется чертежами, где:

фиг.1 - трехкоординатный датчик (IМSС) магнитного (Н) поля;

фиг.2 - трехкоординатный датчик (IСЕ) электрического (Е) поля;

фиг.3 - одна из реализаций измерений физического поля по трассе полета (l) над очаговой зоной;

фиг.4 - определение гипоцентра как точки пересечения векторов переноса энергии нисходящего и восходящего витков;

фиг.5 - функции фрактальной размерности физического поля: а) невозмущенного, б) аномального;

фиг.6 - динамика изменения фрактальной размерности синтезированной матрицы;

фиг.7 - функциональная схема устройства, реализующего способ.

Техническая сущность способа состоит в следующем.

Любое событие материального мира оставляет информационный след. На этом свойстве материи основаны телепатические методы передачи информации (см., например, Грабовой Г.П. Система беспроводной передачи информации. Патент RU №2.163.419, 2000 г.), экстрасенсорные обследования биополя человека для выявления заболевания и др. Чем больше энергетика объекта наблюдения, тем менее зашумленным оказывается его информационный след. Очаг землетрясения аккумулирует огромную энергию тектонических напряжений. В потенциальном поле механических напряжений, в окрестностях очаговой зоны, наблюдаются аномалии других физических полей: электрического, магнитного, гравитационного. Следует ожидать, что при наличии объективных способов выделения скрытой информации можно визуализировать и прогнозировать процессы, связанные с подготовкой таких энергетически мощных явлений природы, как землетрясения. Установлено, что психологическое восприятие образа человеком-оператором происходит на уровне контурного рисунка. Следовательно, наиболее информационно емким признаком объекта является его форма (топология). Узор рисунка объекта, его орнамент обеспечивают достоверную идентификацию образа на фоне многообразия других образов, например лица человека среди миллионов других лиц. Топологическим признаком объекта является введенная Мандельбротом фрактальная размерность [см., например, Мandelbrot В. Fгасtаls fоrms. Сhаnсе аnd Dimension. Freeman, Sаn-Francisco, 1997].

Под фракталом понимают минимальный структурный элемент множества, содержащий все его признаки и самоподобно воспроизводящейся при аффинных преобразованиях (масштабирование, сдвиг, поворот). В математике для количественной оценки фрактальной размерности используют так называемую размерность Хаусдорфа [см., например, Р.А.Вurrough. Fractal dimensions of landscapes and other еnvironmental data. Nаturе 294, 1981, р.240]. По определению размерность Хаусдорфа вычисляется:

где ε - размер ребра элементов измерения, которыми покрывается объект (например площадь квадратика, объем кубика);

Ω _ε - число элементов измерения размером ε , содержащих хотя бы одну точку объекта.

Аномальные процессы изменяют структуру природного образования, картину физического поля и производные от него - параметры сигнала в пространственных координатах. Вследствие этого фрактальные размерности двух видов физического поля - эталонного и измененного будут отличаться. На фиг.1 и 2 представлены датчики для измерения электрической Е и магнитной Н составляющих физического поля в трех взаимно ортогональных плоскостях. Совокупность дискретных отчетов Е(l) и Н(l) по трассе полета КА над очаговой зоной образует массив измерений, подлежащий обработке. Вид одной из возможных реализации Е(l) иллюстрируется фиг.3. Изменение физической картины поля так или иначе связано с энергетическим воздействием на него очаговой зоны. В качестве характеристики физического поля используют вектор, равный произведению составляющих К=Н× Е, длина которого в любой точке равна произведению соответствующих проекций:

R_i=Н_xiЕ_хi+Н_yiЕ_yi+Н_ziЕ_zi

Каждый вектор характеризуется величиной (длиной) и направлением. Направление вектора соответствует направлению переноса энергии в окружающем пространстве. Его определяют путем обработки массива зарегистрированных измерений. По физическому смыслу дисперсия сигнала представляет собой мощность переменной составляющей: Вычисляя дисперсию сигнала по соответствующим координатам, рассчитывают направляющие косинусов вектора в пространстве относительно плоскости орбиты витка: Направление вектора переноса энергии определяют в двух взаимно ортогональных плоскостях. Поскольку основные сейсмоопасные регионы планеты располагаются в низких широтах, то для этих широт плоскости орбит восходящего и нисходящего витков практически перпендикулярны. Пересечение векторов R восходящего и нисходящего витков определяет фазовый центр возмущений физического поля, который отождествляют с гипоцентром очага. Поскольку возмущения физического поля от Солнца и других планет не имеют фазового центра на поверхности Земли, то пересечение векторов однозначно указывает на источник аномалии, имеющий земное происхождение. Процедура определения фазового центра возмущений, идентифицируемого как проекция гипоцентра очага землетрясения на околоземное пространство, иллюстрируется фиг.4. Предсказать землетрясение - это значит рассчитать параметры предстоящего удара. Существуют два принципиально различных подхода по расчету характеристик ожидаемого землетрясения по данным об аномальных полях.

Первый подход основан на зависимости Гутенберга-Рихтера, связывающий магнитуду землетрясения со временем существования признака предвестника. В частности, для различных предвестников (более 1000 реализаций) получены эмпирические коэффициенты для формулы Гутенберга-Рихтера [см., например, “Краткосрочный прогноз катастрофических землетрясений с помощью радиофизических наземно-космических методов”, Доклады конференций, О.И.Ф.З. им. О.Ю.Шмидта, РАН, М, 1998 г., стр.9-13]. Для сейсмических волн (колебательного процесса) зависимость для расчета магнитуды удара имеет вид:

lg t_y[сут]≅0,54М-3,37,

где t_y - время существования признака предвестника, отсчитываемое от момента его появления до удара. Второй подход устанавливает связь размеров (Q, км) области сейсмического возбуждения с магнитудой:

lg Q≅ 0,46М-0,35.

Как отмечалось выше, в качестве топологического признака-предвестника аномалии физического поля предложено использовать фрактальную размерность синтезированного массива данных измерений R=Н× Е, Для вычисления фрактальной размерности использован алгоритм расчета методом вариаций.

Результат программного расчета иллюстрируется фиг.5, где представлены функции фрактальной размерности: а) невозмущенного физического поля, б) аномального поля.

Переход от невозмущенного состояния к аномальному сопровождается количественным изменением отслеживаемого признака-предвестника - фрактальной размерности. Сам признак-предвестник и скорость изменения его во времени связаны дифференциальным уравнением первой степени. Из математики известно [см., например, Н.С. Пискунов “Дифференциальное и интегральное исчисления для втузов”, т.1, 5-е издание, Наука, М., 1964 г, стр.158], что общим решением линейного дифференциального уравнения первой степени является экспонента. Начальными условиями для экспоненты являются постоянная времени Т и установившееся значение D₀. Начальные условия определяют по серии последовательных во времени t₁ t₂ t₃ измерений над очаговой зоной. Из свойств экспоненты следует, что

Динамика отслеживаемого процесса иллюстрируется фиг.6. Если интервалы между последовательными измерениями t₁ t₂ t₃ выбрать равными (например, осуществлять регистрацию на смежных витках, через 1,5 часа), то из уравнения экспоненты можно рассчитать, что Из уравнения экспоненты следует, что с вероятностью 0,99 время установления переходного процесса t_y≅4,7 Т, которое является расчетным для определения магнитуды.

Пример реализации способа

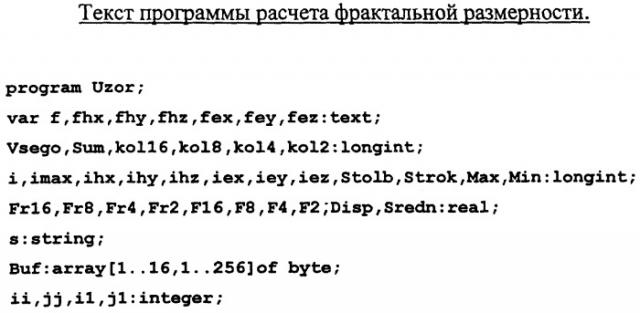
Заявляемый способ может быть реализован на базе системы зондирования по схеме фиг.7. Функциональная схема системы (фиг.7) содержит группировку космических аппаратов 1 (типа "Вулкан"), на каждом из которых установлены датчик 2 (типа IМSС, Франция) и датчик 3 (типа IСЕ, Франция) измерений магнитной и электрической составляющих околоземного космического пространства в трех взаимно ортогональных плоскостях. Включение датчиков в режим измерений над заданным районом земного шара осуществляют по суточной программе или разовым командам, закладываемым в бортовой комплекс управления (БКУ) 4 посредством радиолинии управления 5 из центра управления полетом (ЦУП) 6. Последовательность отчетов измеряемых параметров записывают в бортовое запоминающее устройство 7 (типа "Нива") и в сеансах видимости КА передают телеметрической системой 8 (типа "БИТС") по автономной радиолинии 9 на наземные пункты приема информации 10, где записывают на магнитофон 11 (типа "Арктур"). Затем информацию перегоняют в Геофизический Центр обработки (ГФЦ) 12, где на основе служебных признаков (время съемки, виток, метки бортового времени) формируют массивы измерений для каждого наблюдаемого региона. По запросам потребителей скомпонованные кадры измерений пересылают в региональные центры 13, где создают их долговременный архив 14. Формирование синтезированной матрицы измерений, ее обработку, расчет фрактальной размерности и прогнозирование параметров землетрясения осуществляют на ПВЭМ 15, в стандартном наборе элементов: процессор 16, оперативное запоминающее устройство 17, винчестер 18, дисплей 19, принтер 20, клавиатура 21. Результаты обработки заносят в базу данных, которую выводят на сайт сети "Интернет" 22. Предварительно в постоянное ЗУ 18 ПВЭМ 15 записывают программу расчета фрактальной размерности синтезируемой матрицы (см. в конце описания). Результаты программного расчета функций фрактальной размерности физических полей а) невозмущенного и б) аномального иллюстрируются рисунком фиг.5. Для повышения достоверности обнаружения отслеживаемого события, при допустимой вероятности ложной тревоги, назначают порог, величину которого выбирают в зависимости от широты и долготы наблюдаемого района. При превышении фрактальной размерности порогового уровня констатируют начало переходного процесса, от момента которого отсчитывают ожидаемое время удара t_y≅4,7 Т. Значения параметров переходного процесса Т и D₀ рассчитывают по серии измерений на последовательных витках. Обработке подвергался массив измерений из 3· 2¹² отсчетов. Пространственное разрешение отсчетов соответствовало разрешению массива измерений способа-аналога порядка 100 м.

Значение фрактальной размерности невозмущенного поля 2,12.

Расчетные значения параметра D в моменты времени t₁ t₂ t₃ соответствовали D₁=2,15, D₂=2,25, D₃=2,326, откуда D₀=2,6, а постоянная времени процесса Т=5,4 час. Ожидаемое время удара t_y=4,7· Т=4,7· 5,4=25,38 час≅ 1,06 сут. Ожидаемая магнитуда удара: lg1,04=0,54М-3,37; М=6,3.

Эффективность способа благодаря измерению нескольких параметров физического поля, а также его формы в протяженном объеме околоземного космического пространства над очаговой зоной существенно выше (по достоверности, точности и статической устойчивости) известных аналогов.

Способ прогнозирования параметров землетрясения, при котором получают регистрограммы дискретных отсчетов характеристик электромагнитных процессов на восходящем и нисходящем витках орбит космического аппарата (КА), проходящих непосредственно через области физических полей, выделяют аномалии физических полей путем расчета фрактальной размерности их изображений и сравнения с эталонными значениями, определяют фазовый центр процесса и характеристики ожидаемого землетрясения по серии регистрограмм, отличающийся тем, что измеряют характеристики магнитного Н (x, y, z) и электрического Е (x, y, z) полей околоземного космического пространства раздельными датчиками в трех взаимно ортогональных плоскостях, формируют синтезированную трехмерную матрицу из скалярных произведений векторов: R_i=Н_xiЕ_xi+Н_yiЕ_yi+H_ziE_zi, вычисляют дисперсию сигнала по массиву R(R_i) измерений: и направляющие косинусы вектора переноса энергии:

рассчитывают фрактальную размерность Д синтезированной матрицы и постоянную времени Т ее изменения из соотношения:

прогнозируют время удара t_y=4,7T, магнитуду М из соотношения lg t_y[сут]≅0,54M-3,37 и гипоцентр очага как точку пересечения векторов переноса энергии на восходящем и нисходящем витках, где Δ t=t₂-t₁ - интервал времени между двумя измерениями для формирования синтезированных матриц,

D₁, D₂ - фрактальные размерности синтезированных матриц изображений в моменты t₁, t₂;

D_o - установившееся значение фрактальной размерности накануне удара.