Нейронная сеть для коррекции ошибок в модулярных нейрокомпьютерах

Нейронная сеть для коррекции ошибок в модулярных нейрокомпьютерах

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерных системах.

Известно устройство для контроля и исправления ошибок в избыточном модулярном коде (Патент №2022472, 5 Н 03 М 13/00, RU, БИ №20, 1994), содержащее входной преобразователь кода, вычитатель, выходной преобразователь, блок групп элементов сравнения, блок групп элементов ИЛИ, блок элементов И.

Однако данное устройство обладает следующими недостатками: низкое быстродействие, большие аппаратурные затраты, малые функциональные возможности, так как в устройстве используется один избыточный модуль; коррекция ошибок осуществляется по большому модулю, равному машинному диапазону корректирующих чисел.

Наиболее близким по сущности технического решения к изобретению является устройство для обнаружения ошибок в информации, представленной в системе остаточных классов (А.С. 798846, G 06 F 11/081, СССР, БИ №3, 1981), содержащее входной регистр, кольцевой сдвиговый регистр, преобразователь чисел из системы остаточных классов (СОК) в обобщенную позиционную систему счисления (ОПСС), блок сравнения проекции числа с константой, группы элементов И и ИЛИ.

Недостатком известного устройства является низкое быстродействие, которое определяется вычислением всех n проекций (где n - число оснований СОК).

Цель изобретения - повышение скорости коррекции ошибок в избыточном модулярном коде.

Поставленная цель достигается тем, что в устройство, содержащее нейронную сеть конечного кольца (НСКК), соединенную со входом данных, демультиплексор, нейронную сеть (НС) Хопфилда, мультиплексор, вход которого является выходом НС коррекции ошибок.

Предлагаемое устройство использует метод обнаружения и коррекции ошибок на основе использования модулярных НСКК и НС Хопфилда.

Известные способы обнаружения и коррекции ошибок при использовании избыточной СОК с двумя контрольными основаниями не всегда позволяют исправить одиночную ошибку, если ошибка появилась одновременно с переполнением. Это один из примеров, когда остаточная арифметика не способна полностью решить вопрос абсолютной коррекции ошибочных данных.

Для решения этой проблемы воспользуемся свойствами СОК и НС, а именно обнаружение ошибки проведем на базе свойств СОК, а локализацию и коррекцию ошибки - на базе свойств НС. Архитектура НС обнаружения и коррекции ошибок данных, представленных в модулярном коде, представляет собой многослойную сеть, состоящую из НСКК обнаружения ошибок и НС Хопфилда для локализации и исправления ошибок.

Модулярная НСКК обнаруживает ошибку в данных, представленных в СОК с основаниями р₁, p₂,... , p_n, по значению коэффициентов a_n и a_n-1 обобщенной позиционной системы счисления (ОПСС). Если a_n=a_n-1=0, то ошибки нет, в противном случае ошибка есть.

Сигналы a_n и a_n-1 подаются на управляющие входы демультиплексора и мультиплексора. Если a_n-1=a_n=0, то неискаженные данные через демультиплексор и мультиплексор поступают на выход блока коррекции данных.

Если a_n≠0 или a_n-1≠0, т.е. данные имеют ошибочные разряды, происходит активация управляющих (адресных) входов мультиплексора и демультиплексора, и данные с ошибкой через демультиплексор поступают на вход НС Хопфилда в бинарном коде, т.е. каждый остаточный разряд представлен двоичным кодом. Сеть Хопфилда, обладающая ассоциативным свойством, позволяет восстанавливать искаженные данные. Общая разрядность кода определяется выражением

где: n - количество модулей СОК, p_i - модуль СОК. Сеть Хопфилда состоит из одного слоя нейронов, которые принимают решение асинхронно, связь между ними осуществляется мгновенно и все связи симметричны, т.е. w_ij=w_ji, тогда синаптические веса НС имеют вид

Функционирование сети определяется выражением

где: w_ij - i-й синаптический вес j-ого нейрона; х_i - i-й элемент входного сигнала сети; - i-й элемент входного вектора-образца; y_j - выход j-го нейрона; N - размерность входного вектора; М - количество образцов (разрешенных кодов). Сеть функционирует циклически. В процессе функционирования уменьшается энергетическая функция

В результате релаксационного процесса сеть достигает устойчивого состояния, при котором ни один из ее элементов не меняет своего состояния.

Сеть выбирает эталон с минимальным хэмминговым расстоянием от предъявленного входного вектора путем активации только одного выхода сети, соответствующего этому эталону. Расстояние Хэмминга между двумя бинарными последовательностями Х и X’ определяется как число координат, в которых цифры различны. Хэмминговое расстояние представляет собой пример меры сходства, или, вернее, различия, первоначально введенной для бинарных функций образа в декартовое пространство. Она применима для сравнения любых упорядоченных наборов, принимающих дискретные значения, и, вероятно, является наилучшей из известных мер сходства между цифровыми кодами.

Например, в избыточной СОК, состоящей из 4-х модулей p₁=2, р₂=3, p₃=5, p₄=7, входной набор будет состоять из 9-ти двоичных разрядов. Если взять модули р₃ и р₄ избыточными, тогда рабочий диапазон будет равен р₁·р₂=6, а области разрешенных и запрещенных значений в двоичном коде можно представить в виде

Например, для искаженного вектора X’=(1, 0, 1, 3)=(1, 00, 001, 011), образом является вектор X=(1, 0, 3, 3)=(1, 00, 011, 011), тогда для бинарных последовательностей X и X' хэмминговое расстояние определяется как

Здесь функция ƒ является зависимостью от числа модулей СОК, имеющих в наборах значение "1".

Легко показать, что в данном примере логическая единица будет по модулю р₃=5, т.е. ошибка произошла по этому модулю.

Сеть Хопфилда определяет номер эталона, ближайшего к предъявляемому вектору, таким будет образ (1, 00, 011, 011), так как у него с искаженным вектором наименьшее хэмминговое расстояние. Таким образом, используя ассоциативные свойства и хэмминговое расстояние, сеть Хопфилда локализует и исправляет ошибку. Для увеличения емкости сети и повышения качества распознавания образов можно использовать сети высших порядков.

В качестве входных данных сети Хопфилда можно использовать двоичные сигналы 1 и 0 или вводят обозначения соответственно +1 и -1.

Комбинированный ввод элемента определяется выражением

где s_i обозначает состояние элемента с номером i.

При обновлении состояние изменяется в соответствии с правилом

где s_j - знаковая функция s_j=sign{net_j).

Весовые значения для сети Хопфилда определяются непосредственно из данных, и нет необходимости проведения обучения в более привычном смысле.

Сеть Хопфилда ведет себя как память, и процедура сохранения отдельного вектора представляет собой вычисление прямого произведения вектора с ним самим. Этим самым определяется весовая матрица для сети Хопфилда, в которой все диагональные элементы должны быть установлены равными 0. Итак, весовая матрица, соответствующая сохранению вектора X, задается выражением

где I - единичная матрица.

Рассмотрим способ определения весовых значений сети Хопфилда.

Пример 1. Найти набор весовых значений сети Хопфилда, соответствующий хранению одного бинарного образа Y=100011011, тогда

При вычитании единичной матрицы обнуляем диагональные элементы, и матрица будет иметь следующий вид:

Первый столбец соответствует весовым значениям первого нейронного элемента, второй - второго и т.д. Сеть Хопфилда может работать в синхронном или асинхронном режимах.

Асинхронный режим. Если на вход сети подать неискаженный входной вектор , то все элементы после обновления окажутся в том же состоянии, причем элементы обновятся в случайном порядке. Пусть, в момент времени t₀=1 выберем первый нейронный элемент, состояние которого будет изменяться. Первый элемент обновится путем умножения вектора подсказки на первый столбец матрицы весов, тогда

Видно, что первый элемент остается в том же состоянии. Аналогичным образом можно убедиться, что при обновлении останутся неизменными и остальные элементы.

Теперь рассмотрим, как будет меняться состояние нейронных элементов, если на вход сети поступает искаженный вектор. Элементы обновляются в случайном порядке, но мы для определенности проверки обновления элементов примем естественный порядок, т.е. 1, 2, 3, 4, 5, 6, 7, 8, 9, тогда

Таким образом, элемент 1 останется в том же состоянии. Следующим является элемент 2.

Элемент 2 также находится в том же состоянии. Далее находим s₃=-6, sign(-6)=-1, s₄=-6, sign(-6)=-1. Теперь проверим

Отсюда видно, что нейронный элемент 5 изменил свое состояние с -1 на 1. При дальнейшем функционировании сеть перестает изменять свое состояние, т.е. элементы s₆, s₇, s₈ и s₉ останутся в прежнем состоянии, что говорит о переходе сети в устойчивое состояние.

В результате произошло исправление ошибочного образа со значения X’=(1, 0, 1, 3) до X=(1, 0, 3, 3).

Синхронный режим. В этом режиме функционирование сети можно представить как y(t+1)=sign(s(t))

Пусть, в первом такте на вход сети подается искаженный вектор Y=(100001011), тогда

Во 2,3 и 4 тактах s(1)=s(2)=s(3)=-6, a sign(-6)=-1, т.е. состояние элементов не изменилось. В 5-м такте s(4)=8, a sign(8)=1, т.е. 5-й элемент изменил свое состояние с -1 на 1. Теперь Y=[1 -1 -1 -1 1 1 -1 1 1]. В 6, 7, 8 тактах s(5)=8, s(6)=-8, s(7)=8 и s(8)=8, sign(s(8))=1, sign(s(-8))=-1. После 5-го такта состояние элементов не изменялось. В результате чего произошло исправление 5-го разряда.

Для сохранения нескольких образов в сети Хопфилда необходимо вычислить все прямые произведения для каждого вектора, и полученные таким образом весовые матрицы сложить.

Пример 2. Определить весовую матрицу сети Хопфилда, соответствующую сохранению следующих двух векторов

[-1 1-1-11 -1 -1 1 -1], [1 -1 -1-111-11 1].

Весовая матрица этих векторов имеет вид

сложим матрицы и обнулим диагональные элементы

Можно сделать вывод, что сочетание СОК и НС обеспечивает обнаружение и коррекцию ошибок во всех случаях, когда переполнение диапазона происходит одновременно с появлением ошибки. Предложенный подход позволяет создавать высокопроизводительные и надежные вычислительные структуры.

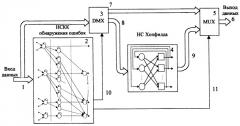
На чертеже приведена НС сеть для коррекции ошибок в модулярных нейрокомпьютерах.

НС состоит из входной шины данных 1, НСКК 2, состоящей из n подсетей (где n - число оснований системы остаточных классов), демультиплексора 3, сети Хопфилда 4, мультиплексора 5, выходной шины данных 6, внутренних шин 7, 8 и 9, шины управления демультиплексором 10, шины управления мультиплексором 11.

Входные данные 1 поступают на вход НСКК 2 и демультиплексор 3. Адресные (управляющие) входы демультиплексора не активны. НСКК 2 вычисляет коэффициенты ОПСС. Если коэффициенты а_n=a_n-1=0, то ошибки нет, формируются адресные сигналы 10,11, которые поступают соответственно на вход демультиплексора 3 и мультиплексора 5. Под действием сигнала 10 демультиплексор 3 коммутирует данные на вход мультиплексора 5, а под действием сигнала 11 - на выход мультиплексора 5, шина 6.

Если во входных данных есть ошибка, то старшие коэффициенты ОПСС a_n и a_n-1, формируемые НСКК 2, не равны 0. При этом на адресные входы демультиплексора 3 по шине 10 поступает код, который коммутирует входные данные на шину 8. Входные данные с ошибкой поступают на вход сети Хопфилда 4, где исправляются, и по шине 9 в исправленном виде поступают на вход мультиплексора 5, который под действием кода, поступающего на адресные входы по шине 11, передает их на вход 6. Итак, обнаружение и исправление ошибки осуществляется за три цикла синхронизации: два цикла синхронизации НСКК и один цикл синхронизации сети Хопфилда, чем и обеспечивается высокая скорость коррекции чисел.

Достоинство данного изобретения перед известным состоит в том, что коррекция числа осуществляется без определения n проекций.

Нейронная сеть для коррекции ошибок в избыточном модулярном коде, содержащая нейронную сеть Хопфилда, демультиплексор, мультиплексор, нейронную сеть конечного кольца, предназначенную для вычисления коэффициентов обобщенной позиционной системы счисления, которые являются адресными сигналами демультиплексора, в которой входные данные поступают на вход нейронной сети конечного кольца и информационные входы демультиплексора, на адресные входы которого поступают управляющие сигналы с выхода нейронной сети конечного кольца, выходы демультиплексора подключены ко входу мультиплексора и входу нейронной сети Хопфилда, выходы которой являются входами мультиплексора, адресные входы которого подключены к управляющему выходу нейронной сети конечного кольца, выходы мультиплексора являются выходами нейронной сети коррекции ошибок в модулярных нейрокомпьютерах.