Нейронная сеть для расширения кортежа числовой системы вычетов

Нейронная сеть для расширения кортежа числовой системы вычетов

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и предназначено для расширения кортежа числовой системы вычетов по введенным дополнительным основаниям и может быть использовано для кодирования данных в модулярных нейрокомпьютерах.

Известно устройство для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления (А.С. №705443 М. Кл². G 06 F 5/02, СССР, БИ №47, 1979), содержащее входной регистр, состоящий из входных регистров по каждому основанию, матрицу элементов И, первую группу элементов ИЛИ, матрицу элементов И второй ступени, вторую группу элементов ИЛИ, выходной регистр, состоящий из выходных регистров по каждому основанию и группы элементов ИЛИ и И. К недостаткам устройства относится сложность и низкая скорость преобразования кодов.

Наиболее близким техническим решением к предложенному является устройство для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления (А.С. №652556 М. Кл². G 06 F 5/02, СССР, БИ №10, 1979), содержащее входной регистр, состоящий из регистров по основаниям, матрицу элементов И первой ступени, первую группу элементов ИЛИ, матрицу элементов И второй ступени, вторую группу элементов ИЛИ, матрицу элементов И третьей ступени, третью группу элементов ИЛИ, матрицу элементов И четвертой ступени, четвертую группу элементов ИЛИ, элементы И и ИЛИ и преобразователь кода.

Недостатком известного устройства является его сложность и низкое быстродействие.

Цель изобретения - упрощение устройства и повышение быстродействия.

Указанная цель достигается тем, что предложенная нейронная сеть содержит входной слой нейронов, нейронные сети конечного кольца для формирования усеченной треугольной матрицы, без учета расширяемого основания, нейронные сети конечного кольца для выполнения модульного суммирования (модульные сумматоры) и нейронную сеть конечного кольца для выполнения финального шага вычисления вычета по дополнительному расширяемому основанию.

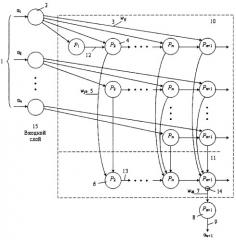
На фиг.1 представлена структура нейронной сети для расширения кортежа числовой системы вычетов, которая содержит входной слой 15 для фиксирования некоторого числа с нейронами 2, на вход которых поступает входной кортеж числовой системы вычетов (а₁, а₂,... ,а_n) 1 нерасширенной системы оснований, треугольную матрицу 10, состоящую из нейронных сетей конечного кольца с нейронами 4, весовыми коэффициентами w_ij 3 и переносами 12, модульные сумматоры 11, состоящие из нейронных сетей конечного кольца с нейронами 6 и переносами 13, весовыми коэффициентами w_jk 5 и выход 14 модулярного сумматора по расширенному основанию р_n+1, в дополнительном коде (p_n+1-a_n+1), где а_n+1 - коэффициенты ОПСС, выходной модулярный сумматор 8 с весовыми коэффициентами 7 и выходом нейронной сети для выполнения финального шага 9 для формирования вычета α _n+1 по расширенному основанию. В настоящее время система остаточных классов (СОК) привлекает все более пристальное внимание из-за ее способности поддерживать высокоскоростную арифметику при параллельной обработке данных. СОК определяется набором модулей p_i из относительно простых чисел.

Пусть р₁, р₂,... ,p_n - попарно взаимно простые целые числа, и α _i=xmodp_i. Тогда соответствие Х→ (α ₁, α ₂,... , α _n) между целыми числами в интервале [0,Р) и набором системы вычетов вида (α ₁, α ₂,... ,α _n), 0<α _i<р_i, 0<i≤ n взаимно однозначно. Кортеж числовой системы вычетов (α ₁, α ₂,... ,α _n) называется модулярным представлением или представлением числа X в СОК.

Основными операциями, выполняемыми в СОК (кроме модульных), являются операции вычисления позиционных характеристик и расширения системы оснований. К ним относятся любые другие немодульные операции, и от времени, затрачиваемого на их выполнение, существенно зависит производительность ЭВМ.

Расширение системы оснований является одной из основных немодульных операций в СОК. Выполнение этой операции бывает необходимо при выполнении ряда других операций, например, при выполнении операции деления чисел, вычислении позиционных характеристик, обнаружении переполнения и других. Кроме того, при обнаружении и исправлении ошибок также необходимо добавление одного или нескольких контрольных оснований.

Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям, т.е. найти остаток от деления на число, если известны остатки от деления на другие числа.

Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычислении остатка от деления на новый модуль. Надо признать, что этот путь не является рациональным с точки зрения числа операций.

Предлагается метод расширения системы оснований, который позволяет определить вычет числа по новому основанию, базируясь на использовании китайской теоремы об остатках (КТО) и обобщенной позиционной системы счисления (ОПСС). Пусть вновь задана система оснований p₁, p₂, ... ,p_n с диапазоном Р=р₁р₂...р_n, ортогональными базисами B₁, B₂, ... , В_n, веса которых m₁, m₂,... , m_n и определяются из сравнения . По определению Пусть в системе задано число А=(α ₁, α ₂,... ,α _n), где α _i=A mod p_i. Расширим систему оснований, добавляя основание p_n+1, тогда диапазон системы станет = р_n+1·Р, ортогональные базисы системы , ,... , , их веса причем . Задача состоит в определении цифры а_n+1 числа А по основанию p_n+1.

Рассмотрим число A в системе оснований p₁, р₂, …,p_n, p_n+1, тогда

где: - диапазон расширенной системы оснований;

- ортогональные базисы расширенной системы оснований.

Представим ортогональные базисы , в обобщенной позиционной системе счисления, тогда

где: - коэффициенты ОПСС;

i,j=1,2,... ,n.

На основании (2) запишем выражение (1) в виде

Из выражения (3) можно определить коэффициенты а_i числа А, тогда

где: α _i - вычеты числа А по mod p_i;

- ортогональные базисы, представленные в ОПСС.

Цифры а_i в представлении ОПСС получаются суммированием по модулю p_i всех произведений и переносом, генерируемым при формировании а_i-1. Перенос генерируется как число раз, когда сумма цифр в ОПСС переполняется по модулю р_i. Этот перенос используется для формирования цифр а_i+1. Последний перенос, генерируемый при получении последней цифры числа в ОПСС, отбрасывается. Рассмотренный метод выполняется в параллельном режиме. Выигрыш в быстродействии данного метода с итеративным методом очевиден, поскольку он уменьшает время преобразования с n циклов синхронизации до трех циклов. Цифры изменяют значения от 0 до р_i-1, причем являются константами, поэтому произведение можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений являются вычеты α _i числа А по модулю р_i.

Для иллюстрации этого метода приведем пример 1.

Пусть p₁=2, p₂=3, р₃=5, р₄=7, ϕ =2· 3· 5· 7=210, B₁=105, B₂=70, B₃=126, B₄=120.

Тогда на основании (2) определим :

Пусть А=11=(1, 2,1,4). Тогда в ПЗУ поместим следующие числа:

Преобразование числа А из СОК в ОПСС имеет вид

Рассмотрим метод определения вычета по расширенному основанию. Пусть СОК состоит из оснований р₁,р₂...,р_n.Объем диапазона этой системы будет Добавим к числу оснований СОК новое основание р_n+1. Объем диапазона этой системы Тогда любое число х из диапазона [0, ϕ ) в обобщенной позиционной системе счисления представимо в виде Если число х будет лежать в первоначальном диапазоне [0; Р), то в ОПСС цифра а_n+1=0. Этот факт и используется для получения остатка (вычета) от деления числа х на новое основание COK p_n+1.

Пусть число х имело представление (α ₁, α ₂,... ,α _n) по основаниям р₁, р₂,... , р_n. Добавляем новое основание p_n+1, тогда число x=(α ₁, α ₂,... , α _n, ) в системе оснований p₁, p₂,... ,p_n, p_n+1, где - остаток от деления числа х на p_n+i, т.е. искомая цифра по новому основанию.

Для определения этой цифры используем метод перевода числа из СОК в ОПСС, включая неизвестную цифру в проводимые операции. При этом мы параллельно получим цифры ОПСС а₁, а₂,... , а_n и выражение для цифры a_n+1. Но так как по предположению число х∈ [0; Р), то цифра а_n+1=0. Из полученного соотношения и определяем искомую цифру .

Рассмотрим этот метод на примере 2.

Пусть задана система модулей р₁= 2, р₂=3, р₃=5, тогда Р=2· 3· 5=30. И пусть задано число х=11=(1, 2, 1). Расширим систему оснований, добавляя р₄=7. Тогда x=11=(1, 2, 1, ) в системе оснований p₁=2, p₂=3, р₃=5, p₄=7.

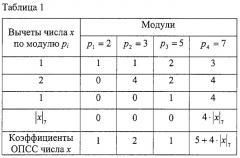
Набор констант b_ij приведен в (5) и задается матрицей

Процесс решения задачи приведен в таблице 1.

Так как но по условию а₄=0, т.е. или

Мультипликативная обратная величина и так как число 5 отрицательное, возьмем его дополнение по модулю 7.

Итак, вычет числа х по модулю 7 определяется выражением

Тогда, расширенное представление числа будет х=11=(1, 2, 1, 4).

Так как результат образования цифры в СОК по новому основанию p_n+i зависит только от первых цифр, то операцию расширения вычетов можно проводить сразу по нескольким основаниям.

Преимущества предложенного метода расширения системы вычетов состоит в том, что:

- все вычисления выполняются в параллельных каналах по отдельным модулям, причем каждый модуль отождествляется с отдельным каналом;

- не требуется вычисления большого количества дополнительных величин, необходимо только наличие констант и мультипликативных величин по расширенным основаниям;

- возможно получение расширенного представления вычетов числа сразу по нескольким дополнительным основаниям, что не влияет на быстродействие всей операции расширения.

Принцип работы нейронной сети для расширения кортежа числовой системы вычетов излагается ниже. Нейронная сеть, приведенная на фиг.1, позволяет определить вычет α _n+1 по дополнительно введенному основанию р_n+1 по известным вычетам (α ₁, α ₂,... ,α _n) 1 исходной системы оснований р₁, р₂, ... ,р_n. Входной кортеж (α ₁, α ₂,... ,α _n) системы вычетов 1 по системе оснований р₁, р₂, ... ,р_n поступает на нейроны 2, расположенные во входном слое 15, а вычет α _n+1 по расширенному основанию р_n+1 появляется на выходе модулярного сумматора 8, выход 9.

С выходов нейронов 2 входного слоя 15 значения вычетов по модулям р₁, р₂, ... ,p_n поступают на входы НСКК, нейроны 4, по соответствующим модулям треугольной матрицы 10. Весовые коэффициенты нейронов 4, выполняющие роль распределенной памяти, определяются значением w_ij=. Нейроны 4 вычисляют значение с учетом переноса 12. Выходные значения НСКК, нейроны 4 треугольной матрицы 10, подаются на вход НСКК с весовыми коэффициентами w_jk=1 для выполнения модульного суммирования 11, нейроны 6, где суммируются согласно правилу сложения цифр в представлении ОПСС, т.е. данные в i-м канале будут суммироваться с учетом переноса 13 в (i-1) канале по модулю р_i в представлении ОПСС.

Перенос представляет собой число раз, превышающее величину модуля p_i, который поступает к (i+1) каналу. Поскольку в каждой строке усеченной треугольной матрицы имеется (i-1) нулей перед первым значащим элементом, а сумма чисел может переноситься (n-1) раз, то абсолютная величина каждого переноса ограничивается величиной (n-1):

где w_ij=.

Из выражения (7) видно, что значение по расширенному основанию α _n+1w_n(n+1) в суммировании не участвует. С выхода НСКК по расширенному модулю, полученное значение суммы в дополнительном коде 14, подается на вход нейронной сети для выполнения финального шага, нейроны 8, весовой коэффициент которого w_kl 7 определяются мультипликативной величиной На выходе нейрона 8 формируется вычет а_n+1 9 по расширенному основанию.

Данное устройство может быть применено для определения вычетов по любому количеству l различных модулей. При этом определенные внешние параметры нейронных сетей для выполнения финального шага вычисления вычета по дополнительным расширенным модулям будут определяться мультипликативной величиной где l –количество расширенных модулей.

Время расширения кортежа числовой системы вычетов по любому количеству модулей определяется тремя циклами синхронизации: один цикл для формирования произведений один цикл для формирования где s=1, 2,... , l и один цикл для выполнения финального шага.

Изобретение преимущественно предназначено для построения функциональных блоков отказоустойчивых модулярных нейрокомпьютеров.

Нейронная сеть для расширения кортежа числовой системы вычетов машинного диапазона модулярного нейрокомпьютера, содержащая входной слой нейронов для фиксирования числа нейронов и вычисления значений вычетов по модулям p₁, p₂, …, p_n, усеченную треугольную матрицу нейронных сетей конечного кольца по модулям системы остаточных классов, нейронной сети конечного кольца по модулям системы остаточных классов, при этом упомянутые нейронные сети конечного кольца предназначены для вычисления значения с учетом переноса, где - коэффициенты обобщенной позиционной системы счисления, - вычеты из числа А по mod p_i, в нее введены нейронные сети конечного кольца для выполнения модульного суммирования по всем основаниям и дополнительному расширяемому модулям и нейронная сеть для выполнения финального шага вычисления вычета по дополнительно расширяемому модулю, отличающаяся тем, что в ней выходы нейронов входного слоя разветвлены на входы нейронных сетей конечного кольца усеченной треугольной матрицы, выполненной в виде распределенной памяти, выходы которых соединены с входами нейронных сетей конечного кольца с единичными синаптическими весами для выполнения модульного суммирования по всем основным и дополнительно расширяемому модулям, выходы переносов которых iмодулей, где i= 2, 3, … n, соединены с входами i+1 модулей, а выход суммы n+1 модуля соединен со входом нейронной сети для выполнения финального шага вычисления вычета по дополнительно расширяемому основанию.