Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе

Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к способам управления летательных аппаратов (ЛА) при их наведении на источники радиоизлучений (ИРИ), в частности к способам управления ЛА в угломерных двухпозиционных радиолокационных системах (УДПРЛС).

В практике применения авиации часто возникают задачи, когда с помощью УДПРЛС необходимо определить местоположение ИРИ с высокой точностью за минимально короткое время. Решение этой задачи во многом зависит от способа управления обоими ЛА, поскольку в процессе их управления изменяются взаимные положения как ЛА, так и ИРИ, значительно влияющие на точность определения местоположения последнего [В.В.Дрогалин, В.А.Ефимов, А.И.Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. - Успехи современной радиоэлектроники. Зарубежная радиоэлектроника, 2003, №5, стр.38].

Известен способ управления двух ЛА по курсу в горизонтальной плоскости (прототип) [Катулев А.Н., Тухватулин В.В. Формирование управлений движением пеленгаторов угломерной системы // Радиотехника, 1989, №10, стр.3-5], согласно которому:

на каждом из ЛА измеряют пеленг ИРИ и собственные координаты ЛА;

измеренные значения пеленга ИРИ и координат ЛА оценивают;

осуществляют взаимный обмен между ЛА оцененными значениями пеленгов ИРИ и координат ЛА;

по оцененным значениям пеленгов ИРИ и координат ЛА на каждом ЛА формируют сигналы управления движением каждого ЛА таким образом, что в каждый момент времени обеспечивается минимум корреляционной матрицы ошибок измерений координат ИРИ.

Недостатки прототипа:

- достаточно сложная процедура нахождения значений оптимальных перемещений летательных аппаратов, при которых достигается максимально быстрое убывание нормы корреляционной матрицы ошибок измерений;

- способ, из-за наличия нелинейных преобразований при формировании сигналов управления ЛА, накладывает существенные ограничения на допустимые максимальные ошибки измерений пеленгов: при средней квадратичной ошибке (СКО) измерения пеленга больше 15 угловых минут возможны срывы управления;

- достаточно жесткие требования к характеру движения пеленгуемого ИРИ: допускается лишь равномерное и прямолинейное движение ИРИ;

- способ не учитывает того, что при формировании сигналов управления ЛА необходимо одновременно решать две задачи: управление ЛА с целью обеспечения минимального времени подлета наводимого на ИРИ летательного аппарата и формирование таких траекторий движения обоих ЛА, при которых создаются условия для наиболее точного для УДПРЛС определения координат ИРИ.

В связи с этим актуальна проблема разработки способов управления ЛА, предусматривающих решение задачи управления процессом наблюдения с одновременным наведением на ИРИ. При этом наиболее трудоемким является процесс управления ЛА в горизонтальной плоскости.

Таким образом, задача настоящего изобретения состоит в обеспечении такого наведения летательными аппаратами по курсу в УДПРЛС, при котором обеспечивается минимум времени подлета первого ЛА к ИРИ, а траектория движения другого ЛА обеспечивает условия для наиболее точных измерений координат ИРИ.

Решение поставленной задачи основано на следующем.

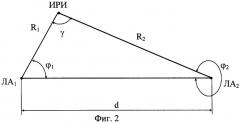
Анализ, выполненный в [В.В.Дрогалин, В.А.Ефимов, А.И.Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. - Успехи современной радиоэлектроники. Зарубежная радиоэлектроника, 2003, №5, стр.25-38] показал, что ошибки определения местоположения ИРИ зависят от взаимного положения летательных аппаратов друг относительно друга и относительно ИРИ, при этом существуют точки нахождения ИРИ относительно летательных аппаратов, в которых оценивание координат ИРИ осуществляется с достаточной для практики точностью. Как показано в приведенной статье, погрешность определения координат ИРИ достигает минимума для точек, лежащих на окружности, радиус которой равен половине расстояния между летательными аппаратами. При таком положении ИРИ относительно ЛА линии пеленгов ИРИ пересекаются под прямым углом (см. фиг.2). При случайных ошибках пеленгации и при использовании в качестве показателя точности СКО местоопределения ИРИ σ _r при одинаковых ошибках пеленгации σ ϕ ₁=σ ϕ ₂=σ ϕ имеет место соотношение [там же, стр.32].

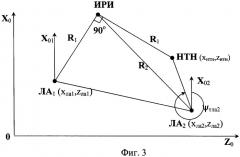
Из приведенной формулы следует, что минимальная СКО местоопределения ИРИ, равная σ _rmin=0,0175σ ϕ d, будет при R₁=R₂ и γ =90° ; т.е. для любого расстояния R₁, оптимальное положение второго ЛА находится на перпендикуляре к направлению пеленга ИРИ из точки нахождения первого ЛА, проходящем через ИРИ. При γ =90° и текущем значении R₁ ошибка местоопределения ИРИ тем меньше, чем меньше R₂, и, следовательно, чем меньше размер базы d. Такой геометрии взаимного расположения ЛА и ИРИ (см. фиг.3) соответствует некоторая точка, называемая в дальнейшем наилучшей точкой наблюдения (НТН), положение которой непрерывно изменяется в пространстве, так как ИРИ и ЛА движутся.

При решении поставленной задачи выбор первого ЛА можно осуществлять различными способами, например, сравнением расстояния от ЛА до ИРИ: первым ЛА считается тот, расстояние от которого до ИРИ меньше (так для взаимного положения ЛА и ИРИ, показанного на фиг.2 и 3, первым ЛА будет ЛА₁, так как R₁<R₂).

Управление первым ЛА может выполняться любым из известных способов самонаведения, например, методом прямого наведения или наведением в наивыгоднейшую точку встречи [Авиационные системы радиоуправления. Т.2. Под ред. А.И.Канащенкова, В.И.Меркулова. - М.: Радиотехника, 2003, стр.15-23].

Управление вторым ЛА при его наведении в НТН также может выполняться любым из известных способов самонаведения (см. там же, 15-23]. Простейшим способом наведения второго ЛА является способ, согласно которому его продольная ось совмещается с направлением на НТН. Для реализации такого наведения необходимо для каждого момента управления вторым ЛА знать x_НТН, z_НТН - координаты НТН, х_ЛА2, z_ЛА2 - координаты второго ЛА в прямоугольной горизонтальной системе координат, Ψ _ЛА2, Ψ _ЛА2 - текущий и требуемый курсы, соответственно, второго ЛА.

Координаты НТН можно найти по формулам:

х_НТН=х_ИРИ-R_зад sin(Ψ _ЛА1-ϕ ₁)

z_НТН=z_ИРИ+R_зад cos(Ψ _ЛА1-ϕ ₁)

где Ψ _ЛА1 - текущий курс первого ЛА,

ϕ _ЛА1 - бортовой пеленг ИРИ из точки нахождения первого ЛА.

Значение требуемого курса Ψ _тЛА2 можно вычислить по формулам

Наличие двух формул для вычисления значений требуемого курса объясняется тем, что курс ЛА может иметь только положительное значение и изменяться в диапазоне от 0 до 360° .

Параметр управления вторым ЛА можно сформировать по формуле

Δ Ψ ₂=Ψ _ЛA2-Ψ _тЛA2,

где Ψ _ЛА2 - курс второго ЛА.

Заявленный технический результат достигается тем, что

- измеряют значения пеленгов ϕ ₁, ϕ ₂ ИРИ соответственно на первом и втором ЛА;

- измеряют координаты х_ЛА1, z_ЛА1 первого и х_ЛА2, z_ЛА2 второго ЛА в прямоугольной горизонтальной системе координат и их курсы Ψ _ЛА1 и Ψ _ЛА2;

- между ЛА осуществляют взаимный обмен результатами измерений пеленгов ϕ ₁, ϕ ₂ ИРИ, координат х_ЛА1, z_ЛА1 и х_ЛА2, z_ЛА2 ЛА и их курсов Ψ _ЛА1 и Ψ _ЛА2;

- на каждом ЛА одним из известных способов, например описанным в [В.В.Дрогалин, В.А.Ефимов, А.И.Канащенков А.И. и др. Алгоритмы оценивания координат и параметров радиоизлучающих целей в угломерных двухпозиционных бортовых радиолокационных системах. - Информационно-измерительные и управляющие системы, 2003, т.1, №1, стр. 4-22], оценивают координаты ИРИ х_ири; z_ири в прямоугольной горизонтальной системе координат и расстояния R₁, R₂ до ИРИ от соответствующего ЛА,

- выбирают (например, методом сравнения расстояний R₁, R₂) ЛА, обеспечивающий минимальное время полета ЛА к ИРИ: если R₁≤R₂, то таким ЛА считают ЛА₁, иначе – ЛА₂.

- осуществляют самонаведение выбранного ЛА на ИРИ одним из известных способов, например описанным в [Авиационные системы радиоуправления. Т.2. Под ред. А.И.Канащенкова, В.И.Меркулова. - М.: Радиотехника, 2003, стр. 15-23];

- находят координаты х_НТН, z_НТН HTH в прямоугольной горизонтальной системе координат по полученным на основе решения геометрической задачи фиг.3 формулам

где Ψ _ЛА1 - курс первого ЛА;

ϕ ₁ - бортовой пеленг ИРИ из точки нахождения первого ЛА;

- рассчитывают значение требуемого курса второго ЛА по полученным на основе решения геометрической задачи фиг.3 формулам

формируют параметр управления вторым ЛА по формуле

Δ Ψ _ЛA2=Ψ _ЛA2-Ψ _тЛA2, (3)

где Ψ _ЛА2 - текущий курс второго ЛА.

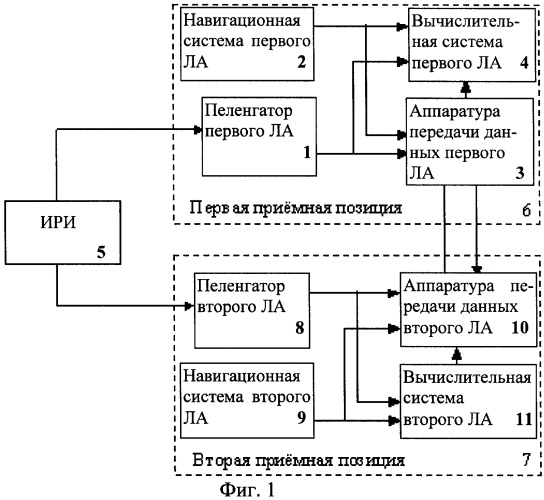
На фиг.1 представлена упрощенная структурная схема возможного варианта построения УДПРЛС, реализующей предлагаемый способ управления, где

1 - пеленгатор первого ЛА;

2 - навигационная система первого ЛА;

3 - аппаратура передачи данных первого ЛА;

4 - вычислительная система первого ЛА;

5 - ИРИ;

6 - первая приемная позиция (ПП);

7 - вторая ПП.

8 - пеленгатор второго ЛА;

9 - навигационная система второго ЛА;

10 - аппаратура передачи данных второго ЛА;

11 - вычислительная система второго ЛА.

На фиг.2 графически показаны величины, входящие в формулу для ошибок оценивания местоположения ИРИ в УДПРЛС, где введены следующие обозначения: R₁ и R₂ - расстояния от ИРИ (точка ИРИ) до первого и второго, соответственно, летательных аппаратов (точки ла₁ и ЛА₂); γ - угол пересечения пеленгов ϕ ₁ и ϕ ₂ ИРИ из точек ЛА₁ и ЛА₂ соответственно; d - база.

Фиг.3 поясняет геометрию наведения ЛА в горизонтальной плоскости, где обозначено: точки ЛА₁, ЛА₂ и ИРИ соответствуют проекциям на горизонтальную плоскость центров масс летательных аппаратов и ИРИ в прямоугольной горизонтальной системе координат X₀OZ₀. Оси ЛА₁X₀₁, ЛА₂Х₀₂ параллельны оси ОХ₀. R₁ и R₂ - расстояния от ИРИ (точка ИРИ) до первого и второго, соответственно, летательных аппаратов (точки ЛА₁ и ЛА₂); Ψ _тЛА2 - требуемый курс второго ЛА.

Рассмотрим возможный вариант функционирования УДПРЛС при использовании заявленного способа управления ЛА по курсу.

В состав УПДРЛС входят первая 6 и вторая 7 подвижные ПП. Каждая ПП содержит одинаковый состав оборудования: пеленгатор 1 (8), навигационную систему 2 (9), аппаратуру передачи данных 3 (10) и вычислительную систему 4 (11).

ИРИ - любое радиоэлектронное средство, излучающее радиосигналы.

Пеленгатор первого ЛА 1 измеряет значение пеленга ϕ ₁ ИРИ, которое с его выхода поступает на первый вход аппаратуры передачи данных 3 первого ЛА и на первый вход вычислительной системы 4 первого ЛА. Пеленгатор 8 второго ЛА также измеряет значения пеленга ϕ ₂ ИРИ, которое с его выхода поступает на первый вход аппаратуры передачи данных 10 второго ЛА и на первый вход вычислительной системы 11 второго ЛА.

Навигационная система 2 первого ЛА определяет координаты х_ЛА1, z_ЛА2 первого ЛА в прямоугольной горизонтальной системе координат и его курс Ψ _ЛА1, которые с ее выхода поступают на второй вход аппаратуры передачи данных 3 первого ЛА и на второй вход вычислительной системы 4 первого ЛА. Навигационная система 9 второго ЛА определяет координаты х_ЛА2, z_ЛА2 второго ЛА в той же системе координат и его курс Ψ _ЛА2, которые с ее выхода поступают на второй вход аппаратуры передачи данных 10 второго ЛА и на второй вход вычислительной системы 11 второго ЛА.

Предпочтительным вариантом для определения координат ЛА является использование спутниковой радионавигационной системы как наиболее точной.

Значение пеленга ϕ ₁ ИРИ, измеренного пеленгатором 1 первого ЛА, значения координат х_ЛА1, z_ЛА1 первого ЛА и значение его курса Ψ _ЛА1 аппаратура передачи данных 3 первого ЛА передает с первой ПП 6 на вторую ПП 7, где их принимает аппаратура передачи данных 10 второго ЛА и передает их на третий вход вычислительной системы 11 второго ЛА.

Значение пеленга ϕ ₂ ИРИ, измеренного пеленгатором 8 второго ЛА, значения координат х_ЛА2, z_ЛА2 второго ЛА и значение его курса Ψ _ЛА2 аппаратура передачи данных 10 второго ЛА передает со второй ПП 7 на первую ПП 6, где их принимает аппаратура передачи данных 3 первого ЛА и предает их на третий вход вычислительной системы 4 первого ЛА.

Вычислительные системы первого 4 и второго 11 ЛА по полученным данным известным способом, например описанным в [В.В.Дрогалин, В.А.Ефимов, А.И.Канащенков А.И. и др. Алгоритмы оценивания координат и параметров радиоизлучающих целей в угломерных двухпозиционных бортовых радиолокационных системах. - Информационно-измерительные и управляющие системы, 2003, т.1, №1, стр.4-22] оценивают координаты ИРИ. Кроме этого, они сравнением расстояний R₁ и R₂ определяют первый ЛА, который будет лететь в направление ИРИ, и второй ЛА, который будет обеспечивать наилучшие условия радиолокационного наблюдения ИРИ.

Вычислительная система 4 первого ЛА по известной формуле [Меркулов В.В., Дрогалин В.В. и др. Авиационные системы радиоуправления. Т.2. / Под ред. Меркулова В.И., Канащенкова А.И. - М.: Радиотехника, 2003, стр. 15]

где к_р - размерный коэффициент, вырабатывает сигнал управления первым ЛА, который используется в системе управления первым ЛА для его наведения на ИРИ.

Вычислительная система 11 второго ЛА по формулам (1) вычисляет координаты x_нтн, z_HTH HTH в прямоугольной горизонтальной системе координат, используя которые по формулам (2) рассчитывает требуемое значение курса второго ЛА Ψ _тЛА2, по которому по формуле (3) формируют параметр управления вторым ЛА, который используется для его самонаведения в HTH.

Таким образом, заявленный способ существенно расширяет возможности практического применения летательных аппаратов в УДПРЛС: он позволяет наводить ЛА на воздушные ИРИ, обеспечивая минимум времени подлета одного из ЛА к ИРИ, при этом не накладывая никаких ограничений на характер его движения. Достоинством способа является также относительная простота его реализации. Кроме того, использование заявленного способа не налагает ограничений на элементную базу и не предъявляет существенных требований к быстродействию и объему памяти вычислительных систем.

Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе, заключающийся в том, что измеряют значения пеленгов ϕ₁, ϕ₂ источника радиоизлучений (ИРИ) соответственно на первом и втором летательных аппаратах (ЛА), измеряют координаты х_ЛА1, z_ЛА1 первого и х_ЛА2, z_ЛА2 второго ЛА в прямоугольной горизонтальной системе координат и их курсы Ψ_ЛА1 и Ψ_ЛА2, между летательными аппаратами осуществляют взаимный обмен результатами измерений пеленгов ϕ₁, ϕ₂ ИРИ, координат х_ЛА1,z_ЛА1 и х_ЛА2, z_ЛА2 летательных аппаратов и их курсов Ψ_ЛА1 и Ψ_ЛА2, на каждом ЛА оценивают координаты ИРИ х_ИРИ, z_ИРИ в прямоугольной горизонтальной системе координат и расстояния R₁, R₂ до ИРИ от соответствующего ЛА, отличающийся тем, что выбирают ЛА, обеспечивающий минимальное время полета ЛА к ИРИ, осуществляют самонаведение выбранного ЛА на ИРИ, находят координаты х_НТН, z_НТН наилучшей точки наведения в прямоугольной горизонтальной системе координат по формулам

х_НТН=х_ИРИ-R₁sin(Ψ₁-ϕ₁); z_НТН=z_ИРИ+R₁cos(Ψ₁-ϕ₁),

где Ψ₁ - курс первого ЛА,

ϕ₁ - бортовой пеленг ИРИ из точки нахождения первого ЛА,

рассчитывают требуемый курс второго ЛА по формулам

и формируют параметр управления вторым ЛА по формуле

ΔΨ_ЛА2=Ψ_ЛА2-Ψ_тЛA2,

где Ψ_ЛA2 - текущий курс второго ЛА.