Цифровой рекурсивный фильтр

Цифровой рекурсивный фильтр

Иллюстрации

Показать все

Реферат

Изобретение относится к цифровой вычислительной технике и может быть использовано в системах цифровой обработки радиотехнических сигналов для решения задач оптимальной нелинейной фильтрации.

Известно устройство [1], недостатком которого является ограниченность функциональных возможностей, обусловленная линейной структурой обрабатываемых процессов.

Наиболее близким по технической сущности к заявленному изобретению является расширенный калмановский фильтр [2], содержащий первый блок формирования суммы, первый и второй блоки формирования матричных функций, первый блок формирования разности, первую линию задержки, первый блок коррекции. Недостатком данного устройства является низкая точность формируемых оценок информационного процесса.

Улучшение точностных характеристик фильтрации случайных процессов является актуальным направлением.

Заявленное изобретение направленно на повышение точности при формировании оценки информационного процесса в измерительных системах, что весьма важно при радиолокационном сопровождении целей, и содержит блоки: первый, второй и третий блоки формирования разности, первый, второй и третий блоки коррекции, блок формирования и выдачи априорных данных, первый, второй и третий блоки формирования суммы, первый, второй, третий, четвертый, пятый и шестой блоки формирования матричных функций, первую, вторую и третью линии задержки, при этом первый, второй, третий и четвертый выходы блока формирования и выдачи априорных данных соединены соответственно со вторым, третьим, четвертым, пятым информационным входами первого, второго и третьего блока коррекции, первый информационный выход первого блока коррекции соединен с первым информационным входом первого блока формирования суммы, выход которого соединен с информационным входом первого блока формирования матричной функции, выход которого соединен с информационным входом первой линии задержки, выход которой соединен со вторым информационным входом первого блока формирования суммы, с седьмым информационным входом первого блока коррекции и с информационным входом второго блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом первого блока коррекции, первый информационный выход второго блока формирования матричной функции соединен со вторым информационным входом блока формирования разности, выход которого соединен с первым информационным входом первого блока коррекции; второй информационный выход первого блока коррекции соединен с восьмым информационным входом второго блока коррекции, выход которого соединен с первым информационным входом второго блока формирования суммы, выход которого соединен с информационным входом третьего блока формирования матричной функции, выход которого соединен с информационным входом второй линии задержки, выход которой соединен со вторым информационным входом второго блока формирования суммы, седьмым информационным входом второго блока коррекции и с информационным входом четвертого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом блока коррекции, первый информационный выход четвертого блока формирования матричной функции соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом второго блока коррекции; второй информационный выход второго блока коррекции соединен с восьмым информационным входом третьего блока коррекции, выход которого соединен с первым информационным входом третьего блока формирования суммы, выход которого является выходом устройства и соединен с информационным входом пятого блока формирования матричной функции, выход которого соединен с информационным входом третьей линии задержки, выход которой соединен со вторым информационным входом третьего блока формирования суммы, седьмым информационным входом третьего блока коррекции и с информационным входом шестого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом блока коррекции, первый информационный выход шестого блока формирования матричной функции соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с первым информационным входом третьего блока коррекции; первый информационный вход первого блока формирования разности, первый информационный вход второго блока формирования разности и первый информационный вход третьего блока формирования разности являются входами устройства.

Одним из способов, способствующих повышению точности фильтров оценки параметров динамических систем, является использование методов решения некорректных задач на основе принципов регуляризации. Эффективность применения регуляризации для непрерывных систем доказана для случая метода А.Н.Тихонова [3] и его разновидности в виде метода итерационной регуляризации [4]. Покажем, как получить уравнения фильтрации с использованием метода итерационной регуляризации для дискретной системы [7].

Пусть динамика измеряемых параметров описывается системой разностных уравнений в дискретном времени

где x(k)=[x¹(k),x²(k),... ,x^M(k)]^T∈Е^M - вектор состояния исследуемой системы;

η (k)=[η ¹(k),η ²(k),... ,η ^M(k)]^T∈Е^M - вектор неизвестных внешних воздействий;

F(x(k),k)=[F^l(x(k),k),F²(x(k),k),... ,F^M(x(k),k)]^T∈Е^M - переходная функция непрерывная вместе с частными производными вектор-функция своих аргументов;

G∈ Е^M×Е^M - матрица интенсивности внешних воздействий;

k, N, M - натуральные числа. Предполагается, что матрица имеет обратную.

Наблюдаемый сигнал, получаемый на выходе модели измерительной системы, описывается дискретным уравнением

где y(k)=[y¹(k),y²(k),... ,y^L(k)]^Т∈E^L - вектор наблюдения,

n(k)=[n¹(k),n²(k),... ,n^L(k)]^Т∈E^L - вектор дискретного белого гауссовского шума с известными локальными характеристиками

M[n(k)]=0,

M[n(k)n^T(l)]=Wδ (k-l),

W - ковариационная матрица размерности L× L,

δ (· ) - векторная дельта-функция;

H(x(k))=[H¹(x(k)),H²(x(k)),... H^L(x(k))]^T∈E^L - сигнальная вектор-функция, непрерывна вместе с частными производными;

L, l - натуральные числа.

Поставим задачу синтеза рекуррентного фильтра оценки x*(k), оптимального в смысле минимума функционала, характеризующего ошибку измерения

В силу непрерывности вектор-функции F(· ) решение уравнения (1) непрерывно зависит от η (k), поэтому функционал ошибки (3) на каждом решении системы (1) непрерывно зависит от η (k). Таким образом, задача определения оценки x^*(k), доставляющей минимум (3), равносильна задаче определения

Задача (1), (2), (4) является некорректно поставленной обратной задачей [5]. Найти значения векторов x^*(k), η ^*(k), путем решения совокупности уравнений (1), (2), (4) в условиях некорректности исходной задачи достаточно сложно, в связи с этим широкое распространение получили итерационные градиентные методы. Однако использование таких методов может привести к расходящейся последовательности приближений. Поэтому применение любого итерационного метода для решения задачи (1), (2), (4) требует определения регуляризирующего семейства операторов, в котором параметром регуляризации является номер итерации.

В соответствии с общим определением регуляризирующего семейства операторов по А.Н.Тихонову [5] будем говорить, что итерационный метод

в котором числовой параметр α _n удовлетворяет условиям

порождает регуляризирующее семейство операторов, в котором параметром является номер итерации, если для любого начального приближения η ₀ и для любого значения погрешности исходных данных σ , удовлетворяющего условию 0<|σ |<σ ₀, σ ₀=const, существует номер n(σ ) такой, что

то есть полученные приближения сходятся к точному решению в норме пространства при стремлении погрешности исходных данных к нулю.

Для реализации итерационного метода (5) требуется определить градиент функционала (3). Согласно [6] выражение для определения градиента в точке η _n(k) имеет вид

gradJ[x_n(k),η _n(k)]=G^Tψ _n(k),

где x_n(k) - решение задачи (1) при η _n(k), а вектор ψ _n(k) определяется из условий

Приняв за нулевое приближение η ₀(k)=0, , запишем итерационную последовательность (5) в развернутой форме для ,

η ₀(k)=0,

η ₁(k)=η ₀(k)-α ₀G^Tψ ₀(k)=-α ₀G^Tψ ₀(k),

η ₂(k)=η ₁(k)-α ₁G^Tψ ₁(k)=-α ₀G^Tψ ₀(k)-α ₁G^Tψ ₁(k),

...

В результате с учетом (7) имеем последовательность дискретных двухточечных краевых задач (ДДТКЗ) вида

ψ _i(N)=0,x_i(0)=x^*(0),

,

Введем обозначение и домножим каждое из уравнений для сопряженных векторов ψ _i на величину α _i, тогда уравнения (8) принимают следующий вид

x_n(k+1)=F(x_nk),k)-GG^Tλ _n,

λ _n(N)=0, x_i(0)=x^*(0),

Для получения алгоритма рекуррентного оценивания вектора состояния необходимо воспользоваться методом инвариантного погружения в дискретном варианте. Заметим, что уравнение для вектор-функций λ в ДДТКЗ (9) записано в обратном времени. Это требует его преобразования к виду, отражающему зависимость λ _n(k+1) от λ _n(k) и x_n(k). Производя соответствующие преобразования с учетом выражения для x_n(k+1) из (9) и используя разложение в ряд Тейлора в окрестности F(x_n(k),k), получим следующую последовательность ДДТКЗ:

x_n(k+1)=F(x_n(k),k)+GG^Tλ _n(k)=β [x_n(k),λ _n(k),k],

x_i(k+1/k)=F(x_i(k),k),

x_i(0)=x^*(0), λ _n(N)=0,

где функции β и γ вводятся для сокращения записи.

Заменим условие на конце λ _n(N)=0 более общим условием λ _n(N)=с и пусть N и с - переменные величины. Тогда значение вектора x_n(N) определяется как функция величин N и с

x_n(N)=r[c,N].

Изменение величины N на N+1 дает приращение Δ с, тогда

Запишем выражение для r(c+Δ c, N+1), используя аппарат конечных разностей

r(с+Δ с,N+1)=r(c,N)+Δ r_c(с,N)+Δ r_N(с,N)+Δ ²r_cN(c,N),

или, учитывая (11), получим

где

Δ r_c(c,N)=r(c+Δ c,N)-r(c,N),

Δ r_N(c,N)=r(c,N+1)-r(c,N),

Δ ²r_cN(c,N)=Δ r_c(c,N+1)-Δ r_c(c,N).

Согласно (10) выражения для Δ х_n и Δ с имеют вид

Разрешить разностное уравнение (12) относительно r(c,N}, т.е. найти общее аналитическое решение, не удается, и обычно обращаются к приближенным методам. Предположим, что r(c,N) линейна по с

где - оценка вектора состояния в момент N, P_n(N) - некоторая матрица размерности М× М.

Вычислим разности, входящие в выражение (12), используя выражение (14)

Подставив выражения (13), (14), (15) в (12), получим

Разлагая β и γ в ряд Тейлора в окрестности и пренебрегая членами порядка выше первого, можно записать уравнение (16) в виде

Соотношение (17) выполняется при с→ 0, поэтому, приравнивая коэффициенты при первой и нулевой степени с, получим разностные уравнения для и P_n(N+1)

Запишем ДДТКЗ (10) для случая, когда k=N, при этом учтем, что это все ДДТКЗ для i=0,... ,n-1 являются разрешенными и соответственно оценки х_i представляют собой известные функции параметра k. Таким образом, имеем

Тогда уравнение (18) преобразуется следующим образом:

где

Введем обозначения

Тогда уравнение (20) запишем в виде

Поскольку разницы в переобозначении матриц Р_n и нет, запишем последовательность уравнений для оценки , процесса (1), предполагая, что N постоянно изменяется и k=N, в виде

Последовательность уравнений (22) представляет собой цифровой итеративный фильтр, который позволяет осуществить процесс цифровой обработки измерительной информации для дискретных динамических систем. Если сравнить полученные уравнения с уравнениями дискретного фильтра Калмана, то становится ясно, что они отличны друг от друга за счет возникновения дополнительных связей оценки с совокупностью предыдущих оценок , учитываемых с весовыми коэффициентами, определяемыми последовательностью параметров α _i, и изменяющих общий коэффициент обратной связи в уравнении для оценки . Таким образом, выбор последовательности параметров α _i, удовлетворяющих условиям

позволяет реализовать фильтр цифровой обработки измерительной информации повышенной точности. Следует отметить, что полученный результат предполагает, что исходная система, параметры которой подлежат оценке, нелинейна. Алгоритм (22) дает оптимальную для нелинейной системы оценку параметров в смысле минимума функционала, характеризующего среднеквадратическую ошибку измерительного канала. В отличие от него фильтр Калмана дает лишь первое приближение оптимальной оценки и таким образом является менее точным.

Оценка эффективности функционирования разработанного фильтра произведена на основе численного моделирования задачи определения неизвестного постоянного параметра d дискретной нелинейной системы третьего порядка

x(k+1)=x(k)+τ · r(k)+τ · η ¹(k),

d(k+1)=d(k)+τ · η ³(k),

где параметр τ имеет смысл интервала времени, через который поступает измерительная информация в виде

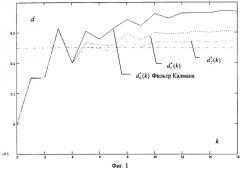
Моделирование проводилось для значений параметров α ₀=1, α ₁=0.333, α ₂=0.1. Графики оценок параметра d=0.25 для i=0,1,2 приводятся на фиг.1 при τ =0.3 при общем интервале T=5. Визуальный анализ показывает, что оценка превосходит по точности оценку .

Таким образом, как следует из соотношений (22), введение новых структурных элементов и связей позволяет в совокупности с общими признаками получить технический результат, состоящий в уменьшении дисперсии ошибок полученных на выходе фильтра оценок входных процессов.

Заявленное устройство может быть применено в информационных системах, связанных со сбором и обработкой информации, например, в информационных системах радиолокационных и радионавигационных комплексов.

Сущность изобретения поясняется фиг.2-6, где представлены структурные схемы итеративного цифрового фильтра, первого, второго и третьего блоков коррекции, блока расчета точностных характеристик.

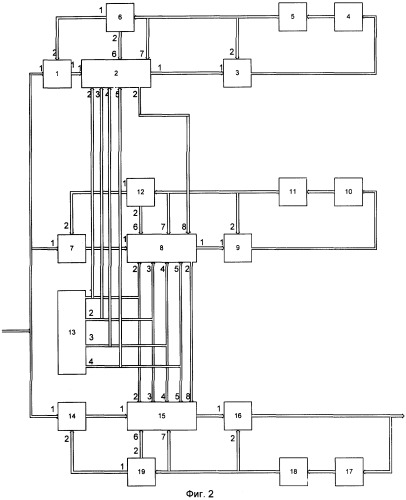
На фиг.2 представлена структурная схема цифрового итеративного фильтра. Устройство содержит первый блок 1, второй блок 7 и третий блок 14 формирования разности, первый блок 2, второй блок 8 и третий блок 15 коррекции, первый блок 3, второй блок 9 и третий блок 16 формирования суммы, первую линию задержки 5, вторую линию задержки 11 и третью линию задержки 18, первый блок 4, второй блок 6, третий блок 10, четвертый блок 12, пятый блок 17 и шестой блок 19 формирования матричных функций, блок 13 формирования и выдачи априорных данных.

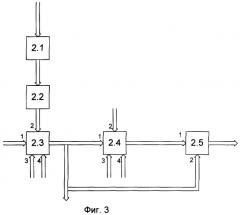
На фиг.3 представлена структурная схема первого блока коррекции, которая содержит блок 2.1 формирования частных производных, блок 2.2 транспонирования матричной функции, блок 2.3 формирования произведения, блок 2.4 вычисления точностных характеристик, блок 2.5 формирования произведения.

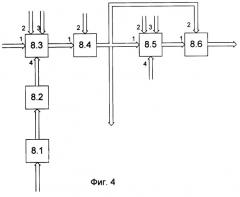
На фиг.4 представлена структурная схема второго блока коррекции, который содержит блок 8.1 формирования частных производных, блок 8.2 транспонирования матричной функции, блок 8.3 формирования произведения, блок 8.4 формирования суммы, блок 8.5 расчета точностных характеристик, блок 8.6 формирования произведения.

На фиг.5 представлена структурная схема третьего блока коррекции, который содержит блок 15.1 формирования частных производных, блок 15.2 транспонирования матричной функции, блок 15.3 формирования произведения, блок 15.4 формирования суммы, блок 15.5 расчета точностных характеристик, блок 15.6 формирования произведения.

На фиг.6 представлена структурная схема блока расчета точностных характеристик, входящего в первый, второй и третий блоки коррекции, который содержит блок 20 формирования частных производных матричной функции, блок 21 транспонирования матриц, блок 22 формирования произведения, линию 23 задержки, блок 24 транспонирования матриц, блок 25 формирования произведения, блок 26 формирования суммы, блок 27 формирования частных производных матричной функции, блок 28 формирования произведения, блок 29 формирования разности, устройство 30 обращения матриц, блок 31 формирования произведения.

Первый, второй, третий, четвертый информационные выходы блока 13 формирования и выдачи априорных данных (фиг.2) соединены соответственно со вторым, третьим, четвертым, пятым информационными входами первого блока 2, второго блока 8 и третьего блока 15 коррекции, второй информационный выход первого блока 2 коррекции соединен с восьмым информационным входом второго блока 8 коррекции, выход которого соединен с первым информационным входом второго блока 9 формирования суммы, выход которого соединен с информационным входом третьего блока 10 формирования матричной функции, выход которого соединен с информационным входом второй линии 11 задержки, выход которой соединен со вторым информационным входом второго блока 9 формирования суммы, с седьмым информационным входом второго блока 8 коррекции и информационным входом четвертого блока 12 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом блока 8 коррекции; первый информационный выход четвертого блока 12 формирования матричной функции соединен со вторым информационным входом второго блока 7 формирования разности, выход которого соединен с первым информационным входом второго блока 8 коррекции; первый информационный выход первого блока 2 коррекции соединен с первым информационным входом первого блока 3 формирования суммы, выход которого соединен с информационным входом первого блока 4 формирования матричной функции, выход которого соединен с информационным входом первой линии 5 задержки, выход которой соединен со вторым информационным входом первого блока 3 формирования суммы, с седьмым информационным входом первого блока 2 коррекции и информационным входом второго блока 6 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом первого блока 2 коррекции; первый информационный выход второго блока 6 формирования матричной функции соединен со вторым информационным входом блока 1 формирования разности, выход которого соединен с первым информационным входом первого блока 2 коррекции; второй информационный выход второго блока 8 коррекции соединен с восьмым информационным входом третьего блока 15 коррекции, выход которого соединен с первым информационным входом третьего блока 16 формирования суммы, выход которого является выходом устройства, а также соединен с информационным входом пятого блока 17 формирования матричной функции, выход которого соединен с информационным входом третьей линии 18 задержки, выход которой соединен со вторым информационным входом третьего блока 16 формирования суммы, с седьмым информационным входом третьего блока 15 коррекции и информационным входом шестого блока 19 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом блока 15 коррекции; первый информационный выход шестого блока 19 формирования матричной функции соединен со вторым информационным входом третьего блока 14 формирования разности, выход которого соединен с первым информационным входом третьего блока 15 коррекции; первый информационный вход первого блока 1 формирования разности, первый информационный вход второго блока 7 и первый информационный вход третьего блока 14 формирования разности являются входами устройства.

Первый и второй информационные выходы блока 13 формирования и выдачи априорных данных соединены с третьим и четвертым информационными входами блока 2.3 формирования произведения (фиг.3); информационный выход первого блока 1 формирования разности соединен с первым информационным входом блока 2.3 формирования произведения; второй информационный выход второго блока 6 формирования матричной функции соединен с информационным входом блока 2.1 формирования частных производных, выход которого соединен с информационным входом блока 2.2 транспонирования матричной функции, выход которого соединен со вторым информационным входом блока 2.3, выход которого соединен с первым информационным входом блока 2.4 расчета точностных характеристик, выход которого соединен с первым информационным входом блока 2.5 формирования произведения, выход которого является выходом первого блока 2 коррекции; информационный выход линии задержки 5 (фиг.2) соединен со вторым информационным входом блока 2.4 расчета точностных характеристик; третий и четвертый выходы блока 13 формирования и выдачи априорных данных соединены с третьим и четвертым информационными входами блока 2.4 расчета точностных характеристик; выход блока 2.3 формирования произведения соединен со вторым информационным входом блока 2.5 формирования произведения и вторым информационным входом блока 8.4 формирования суммы (фиг.4).

Информационный выход второго блока 7 формирования разности соединен с первым информационным входом блока 8.3 формирования произведения (фиг.4). Первый и второй информационные выходы блока 13 формирования выдачи априорных данных соединены со вторым и третьим информационными входами блока 8.3 формирования произведения; второй информационный выход четвертого блока 12 формирования матричной функции соединен с первым информационным входом блока 8.1 формирования частных производных, выход которого соединен с информационным входом блока 8.2 транспонирования матричной функции, выход которого соединен с четвертым информационным входом блока 8.3, выход которого соединен с первым информационным входом блока 8.4 формирования суммы, второй информационный вход которого соединен с информационным выходом блока 2.3 (фиг.3), выход блока 8.4 формирования суммы соединен с первым информационным выходом блока 8.5, со вторым информационным входом блока 15.4 формирования суммы (фиг.5), а также со вторым информационным выходом блока 8.6 формирования произведения; третий и четвертый информационные выходы блока 13 формирования выдачи априорных данных соединены со вторым и третьим информационными входами блока 8.5 расчета точностных характеристик; информационный выход линии задержки 11 соединен с четвертым информационным входом блока 8.5 расчета точностных характеристик, выход которого соединен с первым информационным входом блока 8.6 формирования произведения, выход которого является выходом второго блока 8 коррекции (фиг.2).

Информационный выход третьего блока 14 формирования разности соединен с первым информационным входом блока 15.3 формирования произведения (фиг.5). Первый и второй информационные выходы блока 13 формирования выдачи априорных данных соединены со вторым и третьим информационными входами блока 15.3 формирования произведения; второй информационный выход шестого блока 19 формирования матричной функции соединен с первым информационным входом блока 15.1 формирования частных производных, выход которого соединен с информационным входом блока 15.2 транспонирования матричной функции, выход которого соединен с четвертым информационным входом блока 15.3, выход которого соединен с первым информационным входом блока 15.4 формирования суммы, второй информационный вход которого соединен с информационным выходом блока 8.4 (фиг.4), выход блока 15.4 формирования суммы соединен с первым информационным выходом блока 15.5, а также со вторым информационным выходом блока 15.6 формирования произведения; третий и четвертый информационные выходы блока 13 формирования выдачи априорных данных соединены со вторым и третьим информационными входами блока 15.5 расчета точностных характеристик; информационный выход линии задержки 18 соединен с четвертым информационным входом блока 15.5 расчета точностных характеристик, выход которого соединен с первым информационным входом блока 15.6 формирования произведения, выход которого является выходом второго блока 15 коррекции (фиг.2).

Выход блока 2.3 формирования произведения (фиг.3) соединен с информационным входом блока 27 формирования частных производных (фиг.6), выход которого соединен с информационным входом блока 28 формирования произведения, выход которого соединен с первым информационным входом блока 29 формирования разности, выход которого соединен с информационным входом устройства 30 обращения матриц, выход которого соединен с первым информационным входом блока 31 формирования произведения, выход которого является выходом блока 2.4 (фиг.3) расчета точностных характеристик; четвертый выход блока 13 формирования и выдачи априорных данных соединяется с вторым информационным входом блока 29 формирования разности; выход блока 31 формирования произведения соединен с информационным входом линии 23 задержки, выход которой соединен с третьим информационным входом блока 22 формирования произведения, выход которого соединен со вторым информационным входом блока 26 формирования суммы, выход которого соединен со вторыми информационными входами блоков 28 и 31 формирования произведения; выход первой линии задержки 5 (фиг.2) соединен с информационным входом блока 20 формирования частных производных, выход которого соединен с информационным входом блока 21 транспонирования матриц и первым информационным входом блока 22 формирования произведения, второй информационный вход которого соединен с выходом блока 21; третий информационный выход блока 13 формирования и выдачи априорных данных соединен с информационным входом блока 24 транспонирования матриц и вторым информационным входом блока 25 формирования произведения, первый информационный вход которого соединен с информационным выходом блока 24; выход блока 25 соединен с информационным входом блока 26 формирования суммы.

Блоки 8.5, 15.5 расчета точностных характеристик (фиг.4, 5) имеют структуру и связи, аналогичные блоку 2.4.

Устройство работает следующим образом (фиг.2). В исходном состоянии в блоке 13 формирования и выдачи априорных данных записаны значения матриц W^-1, G, I и значения α ₁, α ₂, α ₃. Значение оценки информационного процесса в (k+1)-й момент времени с выхода блока 3 формирования суммы поступает на вход блока 4 формирования матричной функции, с выхода которого значение поступает на вход линии задержки 4, с выхода которой значение поступает на вход блока 3 формирования суммы, вход блока 2 коррекции и вход блока 6 формирования матричной функции , значение которой с выхода блока 6 поступает на вход блока 2 и на вход блока 1, на выходе которого формируется значение невязки измерения, которое поступает на вход блока 2 коррекции, на остальные входы которого поступают значения α ₁, G, W^-1, I; в блоке 2 формируется произведение матричного коэффициента усиления и невязки измерения, которое суммируется в блоке 3 со значением , с одного из выходов блока 2 коррекции значение M₁(k+1/k) поступает на вход блока 8 коррекции, в котором формируется значение

которое поступает на вход блока 9; значение на выходе блока 9 поступает на вход блока 10, с выхода которого значение поступает на вход линии задержки 11, на выходе которой формируется значение , которое суммируется со значением (25) в блоке 9, на выходе которого формируется значение ; с выхода блока 11 значение поступает на вход блока 8 коррекции, на вход блока 9 и на вход блока 12, на выходе которого формируется значение , которое подается на вход блока 8 и на вход блока 7 формирования разности, на другой вход которого поступает входное колебание; невязка измерения с выхода блока 7 поступает на вход блока 8, на остальные входы которого поступают значения α ₂, G, W^-1, I; с одного из выходов блока 8 коррекции значение M₂(k+1/k) поступает на вход блока 15 коррекции, в котором формируется значение

которое поступает на вход блока 16; значение на выходе блока 16 поступает на вход блока 17, с выхода которого значение поступает на вход линии задержки 18, на выходе которой формируется значение , которое суммируется со значением (26) в блоке 16, на выходе которого формируется значение ; с выхода блока 18 значение поступает на вход блока 15 коррекции, на вход блока 16 и на вход блока 19, на выходе которого формируется значение которое подается на вход блока 15 и на вход блока 14 формирования разности, на другой вход которого поступает входное колебание; невязка измерения с выхода блока 14 поступает на вход блока 17, на остальные входы которого поступают значения α ₃, G, W^-1, I.

Первый блок 2 коррекции работает следующим образом (фиг.3). Значения матричной функции поступают на вход блока 2.1 формирования частных производных, с выхода которого значения поступают на вход блока транспонирования матричной функции 2.2, с выхода которого значения , невязка измерения и значения α ₁, W^-1 поступают на входы блока 2.3 формирования произведения, с выхода которого значение M₁(k+1/k) поступает на вход блока 2.4 расчета точностных характеристик, на другие входы которого поступают значения G, I, и на выходе которого формируется значение Р₁(k+1), которое поступает на вход блока 2.5 формирования произведения, на другой вход которого поступает значение M₁(k+1/k) с выхода блока 2.3. Выход блока 2.5 является выходом блока 2 коррекции.

Второй блок 8 коррекции работает следующим образом (фиг.4). Значение матричной функции поступает на вход блока 8.1 формирования частных производных, с выхода которого значения поступают на вход блока транспонирования матричной функции 8.2, с выхода которого значения , а также значение невязки измерения , α ₂, W^-1 поступают на вход блока 8.3 формирования произведения, с выхода которого значение поступает на вход блока 8.4 суммирования, на другой вход которого поступает значение М₁(k+1/k); значение

с выхода блока 8.4 поступает на вход блока 8.5 расчета точностных характеристик, на другие входы которого поступают значения G, W^-1, , а на выходе формируется значение P₂(k+1), которое умножается на (28) в блоке 8.6 фор