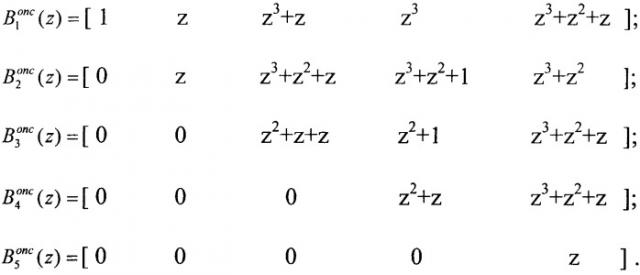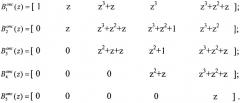Нейронная сеть для вычисления коэффициентов обобщенной полиадической системы, представленных в расширенных полях галуа gf(2v )
Иллюстрации
Показать всеЗаявленное изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для вычисления коэффициентов обобщенной полиадической системы счисления (ОПС), представленных в расширенных полях Галуа GF(2v). Техническим результатом является уменьшение объема оборудования и повышение скорости вычисления коэффициентов ОПС. Для этого нейронная сеть содержит первый входной слой нейронов, и второй слой нейронов, каждый из которых содержит 15 нейронов, взаимосвязанных между собой. 4 табл., 1 ил.
Реферат
Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для вычисления коэффициентов обобщенной полиадической системы (ОПС) счисления, представленных в расширенных полях Галуа GF (2v).
Известна структура нейронной сети, осуществляющей перевод чисел, представленных в системе остаточных классов (СОК) в ОПС (Червяков Н.И., Копыткова Л.Б., Непритимова Е.Н. Нейронные цифровые фильтры с постепенной деградацией их структуры ISSN 0869-5350 / Нейрокомпьютеры: разработка и применение, №10, 2001 г., с.34-44).
Данное устройство содержит входной слой нейронов, нейронную сеть конечного кольца (НСКК) первого яруса и нейронную сеть НСКК второго яруса. Выход последней является выходом устройства, осуществляющего вычисление коэффициентов ОПС.
Недостатком данного устройства является большой объем оборудования и низкая скорость вычисления коэффициентов ОПС.
Данные недостатки связаны в первую очередь с необходимостью учета числа переполнений по основанию СОК рi, i=2,3,...,n при вычислении произведений хiВi, где xi=rest(x/pi), х - исходное число, Вi - ортогональный базис СОК, такой что
Bi=1mod pi,
и переноса этого числа в старший коэффициент ОПС.
Основными задачами, на решение которых направлена заявленная нейронная сеть, являются уменьшение объема оборудования, повышение скорости вычисления коэффициентов ОПС.
Недостаток прототипа можно устранить, если вместо оснований СОК использовать минимальные многочлены, определяемые в расширенных полях Галуа GF(2v). Данные полиномы удовлетворяют всем требованиям, предъявляемым к основаниям системы классов вычетов. Если исходное число А представить в полиномиальной форме A(z), а затем разделить на минимальные многочлены pi(z), i=2,...,n, то полученные остатки, в полиномиальной форме, однозначно будут определять полином A(z) в расширенном поле Галуа GF(gv), то есть
где αi(z)≡A(z)mod pi(z).
В полученной полиномиальной системе класса вычетов (ПСКВ) выполняются операции сложения, вычитания и умножения. Выполнение этих модульных операций совпадает с их реализацией в СОК. Построение ПСКВ и ее нейросетевая реализация приведены в работе (ISSN 0869-5350 Нейрокомпьютеры: разработка и применение. №6, 2003 г., с.61-68. Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей, для исследований ортогональных преобразований сигналов в расширенных полях Галуа).
Если в качестве полей Галуа GF(gv) выбрать расширенные поля с характеристикой g=2, то операция сложения выполнется по модулю два. Таким образом, отсутствие процедуры переполнения по модулю pi(z) при выполнении операции сложения позволяет отказаться от НСКК второго яруса и реализовать процедуру вычисления коэффициентов ОПС с использованием двухслойной нейронной сети.
Пусть задано расширенное поле Галуа GF(24). В данном поле определены минимальные многочлены p1(z)=z+1; p2(z)=z2+z+1; p3(z)=z4+z3+z2+z+1; P4(z)=z4+z3+1; p5(z)=z4+z+1, которые используются в качестве оснований ПСКВ.
Полный диапазон, задаваемый таким основанием, составит
Ортогональные базисы такой системы равны:
B1(z)=z14+zl3+zl2+zll+zl0+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
B2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z;
B3(z)=zl4+zl3+zl2+zll+z9+z8+z7+z6+z4+zз+z2+z;
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3;
B5(z)=zl2+z9+z8+z6+z4+z3+z2+z.
В данном поле GF(24) можно использовать обобщенную полиадическую систему счисления (ОПС) с основаниями:
Р1 *(z)=z+1;
P2 *=P1(z)P2(z)+1;
Р3 *(z)=P1(z)P2(z)Р3(z)=z7+z6+z5+z2+z+1;
P4 *(z)=P1(z)P2(z)Р3(z)P4(z)=z11+z8+z7+z5+z3+z2+z+1
Представим ортогональные базисы в виде коэффициентов ОПС
Согласно Китайской теореме об остатках:
Если в качестве ортогональных базисов Bi(z) взять их представления в ОПС, то в результате выполнения выражения (4) определяются коэффициенты ОПС
где - коэффициенты ОПС i-го ортогонального базиса с учетом переполнения (i-1)-го основания. При этом умножение вычетов αi(z) на соответствующие коэффициенты осуществляется помодульно и поразрядно, при этом учитывается превышение модуля Pi(z) как перенос в старший коэффициент ОПС αi+1(z).
В таблице 1 представлены значения произведения |αi(z)γi(z)|+ pi(z) для всех разрядов αi(z)
| Таблица 1. | ||||||
| основание | разряд | γ1(z) | γ2(z) | γ3(z) | γ4(z) | γ5(z) |
| p1(z)=z+1 | 1 | 1 | z | z3+z | z3 | z3+z2+z |
| p2(z)=z2+z+1 | 1 | 0 | z | z3+z2+1 | z3+z2+1 | z3+z2 |
| Z | 0 | z+1 | z2+1 | z3+z2+z+1 | z3+z2+1 | |
| p3(z)=z4+z3+z2+z+1 | 1 | 0 | 0 | z3+z2+1 | z2+1 | z3+z2+z |
| Z | 0 | 0 | z3+z2+z | z3+z | z3+z2+z+1 | |
| z2 | 0 | 0 | z+1 | z3+z2+1 | z3+z2+1 | |
| z3 | 0 | 0 | z2+z | z+1 | z3+1 | |
| p4(z)=z4+z3+1 | 1 | 0 | 0 | 0 | z2+z | z3+z2+z |
| Z | 0 | 0 | 0 | z3+z2 | zЗ+z2+z+1 | |
| z2 | 0 | 0 | 0 | 1 | z3+z2+1 | |
| z3 | 0 | 0 | 0 | z | z3+1 | |
| p5(z)=z4+z+1 | 1 | 0 | 0 | 0 | 0 | z |
| Z | 0 | 0 | 0 | 0 | z2 | |
| z2 | 0 | 0 | 0 | 0 | z3 | |
| z3 | 0 | 0 | 0 | 0 | z+1 |
В таблице 2 представлено переполнение модуля pi(z) при реализации αi(z)γi(z) для различных разрядов αi(z).
| Таблица 2. | ||||||
| основание | разряд | δ1(z) | δ2(z) | δ3(z) | δ4(z) | δ5(z) |
| p1(z)=z+1 | 1 | 0 | 0 | 0 | 0 | 0 |
| p2(z)=z2+z+1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Z | 0 | 0 | 1 | 1 | 1 | |
| p3(z)=z4+z3+z2+z+1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Z | 0 | 0 | 0 | 0 | 0 | |
| z2 | 0 | 0 | 0 | 1 | 1 | |
| z3 | 0 | 0 | 0 | z | Z+1 | |
| p4(z)=z4+z3+1 | 1 | 0 | 0 | 0 | 0 | |
| Z | 0 | 0 | 0 | 0 | 0 | |
| z2 | 0 | 0 | 0 | 0 | 1 | |
| z3 | 0 | 0 | 0 | 0 | z | |
| p5(z)=z4+z+1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Z | 0 | 0 | 0 | 0 | 0 | |
| z2 | 0 | 0 | 0 | 0 | 0 | |
| z3 | 0 | 0 | 0 | 0 | 0 |
Просуммировав соответствующие ячейки таблицы 1 и таблицы 2, получаем значение γi с учетом переполнения, которые используются в выражении (4). Результаты суммирования приведены в таблице 3.
Пусть дан полином A(z)=z6+z5+z4+z+1, который принадлежит Pпол(z)=zl5+1. Тогда в коде ПСКВ A(z)=(1,z+1,z3+z2+z+1,z3+z2+z,z3+z). Воспользуемся выражением (4) и значениями из таблицы 3 для определения коэффициентов ОПС.
| Таблица 3. | ||||||
| Основание | разряд | γ1 пер(z) | γ2 пер(z) | γ3 пер(z) | γ4 пер(z) | γ5 пер(z) |
| p1(z)=z+1 | 1 | 1 | z | z3+z | z3 | z3+z2+z |
| p2(z)=z2+z+1 | 1 | 0 | z | z3+z2+1 | z3+z2+1 | z3+z2 |
| Z | 0 | z+1 | z2+1 | z3+z2+z+1 | z3+z2+1 | |
| p3(z)=z4+z3+z2+z+1 | 1 | 0 | 0 | z3+z2+1 | z2+1 | z3+z2+z |
| Z | 0 | 0 | z3+z2+z | z3+z | z3+z2+z+1 | |
| z2 | 0 | 0 | z+1 | z3+z2+1 | z3+z2+1 | |
| z3 | 0 | 0 | z2+z | z+1 | z3+1 | |
| p4(z)=z4+z3+1 | 1 | 0 | 0 | 0 | z2+z | z3+z2+z |
| Z | 0 | 0 | 0 | z3+z2 | zЗ+z2+z+1 | |
| z2 | 0 | 0 | 0 | 1 | z3+z2+1 | |
| z3 | 0 | 0 | 0 | z | z3+1 | |
| p5(z)=z4+z+1 | 1 | 0 | 0 | 0 | 0 | z |
| Z | 0 | 0 | 0 | 0 | z2 | |
| z2 | 0 | 0 | 0 | 0 | z3 | |
| z3 | 0 | 0 | 0 | 0 | z+1 |
Тогда в таблице 4 представлены результаты.
| Таблица 4. | |||||
| Модули Pi(z) поля GF | Полином в остатках A(z) | ||||
| p1(z) | p2(z) | p3(z) | p4(z) | p5(z) | |
| 1 | Z | z3+z | z3 | z3+z2+z | 1 |
| 0 | 1 | z3+1 | z2+1 | z2+z | z+1 |
| 0 | 0 | z3+z2 | z | z2+z+1 | z3+z2+z+1 |
| 0 | 0 | 0 | z3+z2+z+1 | Z3 | z3+z2+z |
| 0 | 0 | 0 | 0 | z2+z+1 | z3+z |
| 1 | Z+1 | z3+z2+z+1 | 0 | 0 | Результат |
Таким образом, полином A(z)=(1,z+1,z3+z2+z+1,z3+z2+z,z3+z) представляется в ОПС в следующем виде:
a1(z)=1,a2(z)=z+1,a3(z)=z3+z2+z+1,а4(z)=0,a5(z)=0.
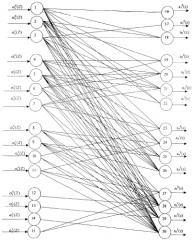
Представленный принцип легко реализуется на нейронной сети прямого распределения. Структура нейронной сети представлена на фигуре 1. Входной слой состоит из 15 нейронов, распределенных в соответствии с размерностью разрядных сеток модулей -1-2-4-4-4. Данные нейроны осуществляют разветвление входного вектора ((α1(z),α2(z),α3(z),α4(z),α5(z)), представленного в двоичной форме. Причем нейрон 1 предназначен для распределения нулевого разряда α1 0(z) первого основания. Нейроны 2, 3 предназначены для распределения нулевого α2 0(z) и первого α2 1(z) разрядов второго основания соответственно. Нейроны 4-7 используются для приема и распределения α3 0(z), α3 1(z), α3 2(z) и α3 3(z) разрядов третьего основания соответственно. Для перераспределения нулевого α4 0(z), первого α4 1(z), второго α4 2(z) и третьего α4 3(z) разрядов четвертого основания p4(z) используются нейроны 8, 9, 10, 11 соответственно. Нейроны 12, 13, 14, 15 применяются для приема нулевого α5 0(z), первого α5 1(z), второго α5 2(z) и третьего α5 3(z) разрядов пятого основания p5(z) соответственно.
Второй слой нейронной сети содержит также 15 нейронов, распределенных в соответствии с размерностью разрядных сеток коэффициентов (αi(z),i=1,2,3,4,5) ОПС -1-2-4-4-4. Нейроны 16-30 второго слоя выполняют базовую операцию суммирования по модулю два значений разрядов, поступающих с выходов соответствующих нейронов первого слоя. Синаптические веса связей равны 1.
Нейрон 16 предназначен для приема данных поступающих с выхода нейрона 1 входного слоя. Выход нейрона 16 соответствует нулевому разряду первого коэффициента ОПС α1(z).
Нейроны 17, 18 осуществляют вычисление нулевого α2 0(z) и первого α2 1(z) разрядов второго коэффициента ОПС соответственно. Причем вход 17 нейрона подключен к выходу 3 нейрона. Вход 18 нейрона подключен к выходу 1, 2, 3 нейронов.
Нейроны 19, 20, 21, 22 осуществляют вычисление нулевого α3 0(z), первого α3 1(z), второго α3 2(z) и третьего α3 3(z) разрядов третьего коэффициента ОПС α3(z) соответственно. Причем нейрон 19 подключен к выходам 2, 4 и 6 нейронов первого слоя. Нейрон 20 - к выходам 1, 4, 5, 6 и 7 нейронов. Вход нейрона 21 - к выходам 2, 3, 4, 5 и 7 нейронов. Вход нейрона 22 - к выходам 1, 2, 5 нейронов.
Нейроны 23, 24, 25, 26 осуществляют вычисление нулевого α4 0(z), первого α4 1(z), второго α4 2(z) и третьего α4 3(z) коэффициента ОПС α4(z) соответственно. Причем входы нейрона 23 подключены к выходам нейронов 2, 4, 7, 10 входного слоя. Вход нейрона 24 - к выходам нейронов 2, 3, 5, 8, 11. Вход нейрона 25 - к выходам нейронов 3, 4, 6, 8, 9. Вход нейрона 26 - к выходам нейронов 1, 2, 3, 4, 5, 6, 9. Нейроны 27, 28, 29, 30 осуществляют вычисление нулевого α5 0(z), первого α5 1(z), второго α5 2(z) и третьего α5 3(z) разрядов третьего коэффициента ОПС α5(z) соответственно. Причем вход нейрона 27 подключен к выходам нейронов 5, 9, 11 и 15 входного слоя. Вход нейрона 28 - к выходам нейронов 1, 3, 5, 7, 8, 9, 11, 12, 15. Вход нейрона 29 - к выходам нейронов 1, 2, 3, 5, 6, 8, 9, 10, 13. Вход нейрона 30 - к выходам нейронов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14 входного слоя.
Выходы нейронов 16-30 второго слоя являются выходами устройства преобразования.
Нейронная сеть для вычисления коэффициентов ОПС, представленных в расширенных полях Галуа, содержащая первый слой нейронов, осуществляющий прием и распределение входного вектора, представленного в виде остатков αi, i=1,2,...,n, второй слой нейронов, осуществляющих суммирование по модулю рi произведения остатков на соответствующие им значения ортогональных базисов, представленных в обобщенной полиадической системе, отличающаяся тем, что в ней используется полиномиальная система класса вычетов, где в качестве модулей используются минимальные многочлены pj(z), j=l,2, определяемые в расширенном поле Галуа GF(2v), причем первый слой нейронной сети содержит 15 нейронов, выходы которых подсоединены к соответствующим входам 15 нейронов второго слоя сети, так что вход первого нейрона второго слоя соединен с выходом первого нейрона первого слоя, вход второго нейрона второго слоя подключен к выходу третьего нейрона первого слоя, вход третьего нейрона второго слоя подключен к выходу 1, 2, 3 нейронов первого слоя, вход четвертого нейрона второго слоя соединен с выходами 2, 4, 6 нейронов первого слоя, вход пятого нейрона второго слоя соединен с выходами 1, 4, 5, 6, 7 нейронов первого слоя, вход шестого нейрона второго слоя соединен с выходами 2, 3, 4, 5, 7 нейронов первого слоя, вход седьмого нейрона второго слоя соединен с выходами 1, 2, 5 нейронов первого слоя, вход восьмого нейрона второго слоя с выходами 2, 4, 7, 10 нейронов первого слоя, вход девятого нейрона второго слоя соединен с выходами 2, 3, 5, 8, 11 нейронов первого слоя, вход десятого нейрона второго слоя соединен с выходами 3, 4, 6, 8, 9 нейронов первого слоя, вход одиннадцатого нейрона соединен с выходами 1, 2, 3, 4, 5, 6, 9 нейронов второго слоя, вход двенадцатого нейрона второго слоя соединен с выходами 5, 9, 11, 15 нейронов первого слоя, вход тринадцатого нейрона второго слоя соединен с выходами 1, 3, 4, 5, 7, 8, 9, 11, 12, 15 нейронов первого слоя, вход четырнадцатого нейрона второго слоя соединен с выходами 1, 2, 4, 5, 6, 8, 9, 10, 13 нейронов первого слоя, вход пятнадцатого нейрона второго слоя соединен с выходами 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14 нейронов первого слоя, выходы нейронов второго слоя являются выходами нейронной сети.