Наземный гравиметрический датчик истинных азимутов и углов отклонения его системы координат относительно вектора силы тяжести

Наземный гравиметрический датчик истинных азимутов и углов отклонения его системы координат относительно вектора силы тяжести

Иллюстрации

Показать все

Реферат

Изобретение относится к методам и средствам ориентации в пространстве на основе гравиметрических измерений в интересах навигации, топографической привязки объектов военной техники (артиллерии, ракет и т.п.) и, непосредственно, в геодезической гравиметрии и геофизической разведке полезных ископаемых.

Целью изобретения является разработка датчика для измерительного преобразования значения силы тяжести и ее составляющих на плоскости его системы координат с целью формирования сигналов:

- значения модуля вектора силы тяжести - для ньютонметра,

- сигнала истинного азимута - для гравикурсоуказателя и

- сигналов об углах наклона осей системы координат датчика относительно вектора силы тяжести - для гравивертиканта.

Для определения сторон горизонта и измерения азимутов направлений используют компасы. Для движущихся объектов ориентация выражается углом между направлением истинного (географического) или магнитного меридиана и направлением движения объекта и носит название соответственно истинного или магнитного курса.

В настоящее время разработано много приборов для определения курса, основанных на разных принципах действия. В авиации, например, применяются компасы: магнитные, индукционные, гиромагнитные, радиокомпасы, астрокомпасы.

Для определения истинного курса существует ряд гироскопических датчиков, носящих название гирокурсоуказателей в отличие от гирокомпасов, назначение которых заключается в определении направления истинного меридиана с максимальной точностью.

Известно, что свободный гироскоп сохраняет свое положение неизменным по отношению к звездам, поэтому если установить ось ротора свободного гироскопа по направлению истинного меридиана, которое из-за суточного вращения Земли непрерывно меняется в мировом пространстве с определенной скоростью в зависимости от географической широты точки места наблюдения, то для того, чтобы измерения были верными, необходимо чтобы главная ось гироскопа прецессировала со скоростью, равной скорости вращения истинного меридиана в точке измерения. Такое явление происходит потому, что горизонтальная плоскость любой сочки земной поверхности (кроме полюса Земли) вращается вокруг полуденной линии (являющейся горизонтальным направлением плоскости меридиана) с угловой скоростью, пропорциональной угловой скорости вращения Земли и синусу угла широты места точки измерения. Например, на экваторе вследствие суточного вращения Земли эта ось будет отклоняться от истинного направления курса с угловой скоростью 0,25°/мин и через 10 мин составит, например, с направлением меридиана угол, равный 2°30'. Поэтому свободный гироскоп непригоден в качестве указателя направления истинного (географического) меридиана без применения специальных корректирующих устройств. Гирокурсоуказатель не дает возможности непосредственно определять направление истинного меридиана. Чтобы определить курс, т.е. азимут направления движения, гирокурсоуказатель должен быть сам предварительно ориентирован на точке местности с известным значением истинного азимута на ориентирную точку. Задача гирокурсоуказателя состоит в том, чтобы возможно точнее и дольше сохранить приданную ему ориентировку относительно истинного меридиана и непрерывно определять истинный азимут (дирекционный угол) движения той платформы, на которой он установлен.

Таким образом, назначение корректирующих устройств заключается, во-первых, в создании внешнего момента, обеспечивающего прецессию главной оси гироскопа с угловой скоростью, равной угловой скорости вращения географического меридиана вокруг направления вертикали в точке измерения, и, во-вторых, в создании корректирующих воздействий, обеспечивающих условия сохранения свойств свободного гироскопа. Поскольку гироскоп является свободным гироскопом только в случае, когда кардановый подвес гироскопа сделан так, что оси вращения его внешней и внутренней рамок и ось вращения гироскопа пересекаются в одной точке, называемой точкой подвеса гироскопа, которая одновременно должна являться центром тяжести системы: гироскоп - кардановый подвес. Главной оси вращения свободного гироскопа можно придать любое направление в пространстве, так как она находится в безразличном равновесии, которое обусловлено совпадением центра тяжести твердого тела с его точкой опоры (точкой подвеса).

Однако ограничения технологических возможностей изготовления гироскопа и условия его эксплуатации из-за неизбежного трения в подшипниках всех осей вращения, вызывающего появления внешних моментов относительно соответствующих осей, а также осевой люфт подшипников, вызывающий смещение центра тяжести относительно точки подвеса, лишают гироскоп, в какой-то степени, свойств его свободы.

Кроме того, необходимо удерживать главную ось гироскопа в горизонтальном положении, так как для определения азимута главной оси используется горизонтальная составляющая угловой скорости вращения ротора гироскопа. Следовательно, чем меньше проекция угловой скорости на плоскость горизонта, тем меньше точность определения азимута.

В механических гирокомпасах гироскоп является чувствительным элементом, определяющим направление меридиана.

В гиромагнитных системах гироскоп не является чувствительным элементом, а применяется в сочетании с магнитным или индукционным компасом и служит по существу стабилизатором, предохраняющим показания магнитного компаса от вредного влияния внешних возмущений.

В гирополукомпасах используется способность гироскопа эффективно сопротивляться внешним возмущениям и в течение некоторого промежутка времени сохранять почти неизменное направление в пространстве. Гирополукомпасы не имеют восстанавливающей силы, которая ориентировала бы их в отношении стран света. Однако в течение некоторого промежутка времени ими можно пользоваться для определения курса, после чего показания гирополукомпаса необходимо корректировать.

Гиромагнитные компасы и гирополукомпасы широко распространены в авиации. Механические гироскопические компасы устанавливают только на морских судах и совершенно не применяют в авиации, так как при современных скоростях полета их погрешности были бы недопустимо велики.

Как погрешности обычных магнитных компасов, так и погрешности гиромагнитных компасов в основном вызываются причинами, которые возникают из-за наличия ферромагнитных деталей на объекте, магнитного склонения и магнитного наклонения, возмущающего действия ускорений и т.п. В гиромагнитных компасах для эффективного уменьшения некоторых погрешностей, в том числе и погрешностей магнитных компасов, используются гироскопические стабилизаторы.

На основе силовой гироскопической стабилизации строятся так называемые трехгироскопные централи (платформы), предназначенные для определения истинного курса и направления вертикали. К недостаткам таких платформ, кроме недостатков, присущих одиночным гироскопам, следует отнести сложность и связанное с этим ухудшение других характеристик. Например, в авиационных гироскопических вертикантах одновременно используются свойства физического маятника устанавливаться в прямолинейном и равномерном полете по направлению истинной вертикали и присущая свободному гироскопу способность сохранять при наличии ускорений неизменным свое положение в пространстве. Такая вертикаль представляет собой астатический гироскоп с маятниковой радиальной коррекцией.

Что касается собственно гирокомпасов, то для этого используют двухстепенные гироскопы (двухстепенные гирокомпасы) и гироскопы со смещенным центром тяжести, так называемые маятниковые гирокомпасы. Как те, так и другие являются сложными электромеханическими устройствами, дорогими и громоздкими, но необходимыми для обеспечения применения других гироприборов, являющихся относительными измерителями.

Анализ средств измерения направления истинного (географического) меридиана, истинных азимутов и вертикали, основанных на использовании, в основном, свойств свободного гироскопа, показывает, что достижение необходимых характеристик достигается дорогой ценой, а в ряде случаев лишает возможность их применения.

Целью предлагаемого изобретения является создание устройства, устраняющего недостатки известных аналогичных по назначению устройств, но основанного на принципиально других физических принципах и, тем самым, расширяющего арсенал таких устройств.

Предлагаемое устройство основано не на использовании свойств свободного гироскопа, сохраняющего в мировом пространстве свое положение, определять угол относительно вращающегося вокруг вертикали точки измерения направления истинного меридиана, а измерения проекций вектора силы тяжести, совпадающей с этой вертикалью, не изменяющей своего положения в точке измерения за счет вращения Земли, на плоскости системы координат предлагаемого устройства, не горизонтированного в пространстве. При этом сразу устраняется фактор влияния углового вращения Земли и необходимость горизонтирования измерителя и вместе с этим значительно уменьшается время на производство измерений. Кроме того, поскольку в предлагаемом устройстве отсутствуют двигатели и другие вращающиеся детали с подшипниками, исчезает влияние трения, существенно улучшаются массогабаритные характеристики, энергопотребление, надежность, стоимость.

Поскольку само предлагаемое устройство не является компасом, а только датчиком курса - курсоуказателем, то требует привязки на исходном (начальном) пункте маршрута, путем использования известных дирекционных углов на ориентирные точки, предварительно определенные с заданной точностью гирокомпасом или астроориентированием.

На первый взгляд, кажется бессмысленным пытаться использовать физический вектор, не имеющий горизонтальных составляющих, каковым является вектор силы тяжести, в качестве источника опорного направления в горизонтальной плоскости.

Но такая возможность существует. Она заключается в использовании свойств измерительных преобразователей, в которых взаимодействие векторов приводит к образованию механического момента, вектор которого перпендикулярен плоскости, в которой они расположены. Математически результат такого взаимодействия выражается векторным произведением взаимодействующих векторов. Примерами таких преобразователей могут служить магнитомеханические преобразователи, преобразователи на основе двухстепенных гироскопов, маятниковые и лепестковые преобразователи гравиметрических и акселерометрических измерителей.

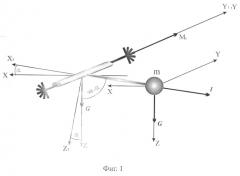
Проиллюстрируем эту возможность. Определим систему координат (СК), в которой расположен вектор силы тяжести таким образом (фиг.1), что сам вектор совпадает с вертикальной осью в месте наблюдения, а из двух ортогональных горизонтальных осей одна - ОХ направлена по направлению северного истинного меридиана, а другая - OY на восток. Пусть система координат акселерометра имеет общее начало с СК вектора G, а северная ось ОХ₁ наклонена к горизонту под углом α и лежит в плоскости меридиана. При этом измерительная ось совпадает с восточной (OY) осью СК вектора силы тяжести. В таком положении на измерительную ось действует механический момент М, пропорциональный значению модуля вектора G и синусу угла α между направлением вектора G и направлением оси чувствительности

M₁=l·G·sin α.

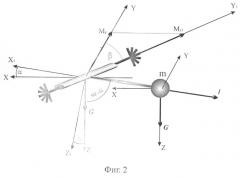
А теперь развернем акселерометр вокруг вертикальной оси OZ на некоторый угол β (фиг.2). Значение измеряемого момента уменьшится пропорционально косинусу угла β: М₂=l·G·sin α·cos β.

Определим этот угол поворота, являющийся истинным азимутом. Если бы мы знали значения модулей векторов G и l и угол α, то по выражению: cos β=М₂/l·G·sin α смогли бы вычислить искомый угол β. Но мы знаем: l - это размер плеча маятника акселерометра, а угол α - это угол установки акселерометра в плоскости меридиана к направлению вектора G, который при горизонтировании основания акселерометра будет постоянным и известным, что позволяет вычислить искомый угол. Но можно вычислить азимут также при последовательном измерении в этих рассматриваемых двух случаях по соотношению измеренных моментов М₁ и М₂:

М₂/M₁=cos β.

Таким образом, возможность использования вектора G для первых шагов достижения поставленной цели не только доказана, но позволяет определить пути полного решения задачи.

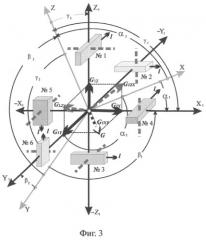
Из анализа рассмотренной ситуации следует, что, для того чтобы подобные измерения можно было бы осуществить не только при расположении измерителя на горизонтальной плоскости, следует обеспечить измерение составляющих вектора G в этих положениях. Это можно решить (фиг.3), если каждой полуоси системы координат измерителя будет соответствовать, подобный, рассмотренному выше, однокомпонентный акселерометр.

Исходя из этого, вырисовывается облик измерителя в следующем виде. На общем основании размещены шесть акселерометров. При этом параллельно каждой полуоси системы координат соответствует измерительная ось (ось поворота) одного акселерометра, ось чувствительности перпендикулярна плоскости, в которой расположены соответствующие оси системы координат измерителя (фиг.4).

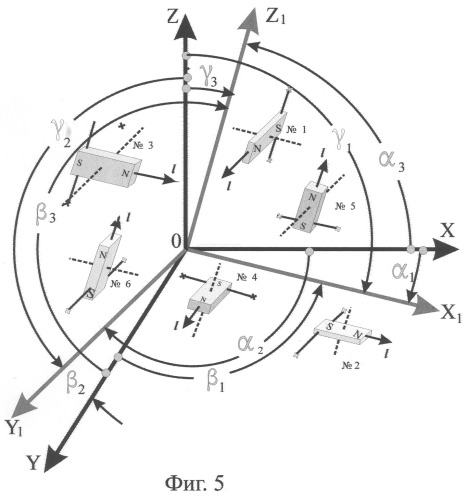
Так как для определения результатов взаимодействия всех шести акселерометров с вектором тяжести при таком положении измерителя в системе координат вектора тяжести необходимо переносить взаимодействующие векторы в одну из систем координат, то возникает необходимость рассмотреть подробнее общий случай взаимного расположения прямоугольных систем координат устройства OX₁Y₁ Z₁ и системы OXYZ, в которой определен вектор силы земного притяжения, имеющих общее начало и различные направления осей координат (фиг.5). Поскольку для определения вектора в любой системе координат достаточно знать координаты точки конца вектора, то возникает вопрос, как, зная координаты какой-либо точки в одной из этих систем, определить координаты той же точки в другой системе. Положение одной системы относительно другой будет определено, если задать углы каждой из осей одной системы относительно другой. Назовем углы оси OX₁ с осями OX, OY, OZ соответственно через α₁, β₁, γ₁; углы оси OY₁ с осями OX, OY, OZ - через α₂, β₂, γ₂; углы OZ₁ с осями OX, OY, OZ - через α₃, β₃, γ₃. Чтобы легче запомнить и пользоваться этими обозначениями, запишем их в форме следующей таблицы.

	x	у	z
x1	α1	β1	γ1
у1	α2	β2	γ2
z1	α3	β3	γ3

В этой таблице каждая буква, стоящая на пересечении горизонтальной строки и вертикального столбца, обозначает угол между осями, указанными в начале строки и столбца; например, буква γ₂ обозначает угол между осями OY₁ и OZ. Девять углов этой таблицы и координаты точки в той и другой системах связаны представленными ниже закономерностями - формулами (1), (2), которые позволяют осуществить переход от одной системы прямоугольных декартовых координат к другой.

На фиг.6 изображены все шесть преобразователей в системе координат измерительного устройства, совмещенной с системой координат вектора силы G, имеющих общее начало координат. Преобразователи изображены схематически в виде лепестков, являющихся их чувствительными элементами. Схематичным является также их попарное расположение на осях системы координат, которое иллюстрирует только тот факт, что каждая такая пара создает суммарный механический момент на одну и ту же ось.

Торсионы изображены в форме ослабленных сечений лепестков, оси поворота параллельны соответствующим осям координат, в плоскости которых размещены лепестки. Взаимное положение лепестков преобразователей соответствует существенным признакам заявленного изобретения. На каждом лепестке преобразователе определено направление вектора l. Перенесем вектор G из своей системы в систему координат вектора преобразователей, пользуясь формулами (1). Любой вектор в любой системе координат определяется координатами точки конца вектора. Применительно к вектору G в его системе координат имеем: Gx=0; Gy=0; Gz=G. Аналогично, каждый из преобразователей в системе координат измерительного устройства имеет соответствующие координаты, отличающиеся друг от друга.

Так, например, для преобразователей №2 и №6 имеем: x₁₂=lx₁₂=l; у₁₂=0; z₁₂=0 (преобр.№2) и x₁₆=0; y₁₆=0; z₁₆=lz₁₆=l (преобр.№6).

Для преобразователей №3 и №1 соответственно:

x₁₃=lx₁₃=l; у₁₃=0; z₁₃=0 (преобр.№3) и х₁₁=0; у₁₁=l; z₁₁=0 (преобр.№1).

Для преобразователей №4 и №5 соответственно:

x₁₄=0; y₁₄=ly₁₄=l; z₁₄=0 (преобр.№4) и x₁₅=0; y₁₅=0; z₁₅=lz₁₅=l (преобр.№5).

В результате переноса вектора G в систему координат вектора измерителя в соответствии с формулами (1) получим:

Gx₁=Gx·cos α₁+Gy·cos β₁+Gz·cos γ₁=Gz·cos γ₁

Gy₁=Gx·cos α₂+Gy·cos β₂+Gz·cos γ₂=Gz·cos γ₂

Gz₁=Gx·cos α₃+Gy·cos β₃+Gz·cos γ₃=Gz·cos γ₃

Исходя из этого, определим проекции создаваемых механических моментов М каждым из преобразователей в результате взаимодействия с вектором G в системе координат измерительного устройства. Для этого воспользуемся общим видом векторного произведения взаимодействующих векторов М=l×G в проекциях на оси декартовой системы координат, в которой определены векторы преобразователей:

Mx₁=ly₁·Gz₁-lz₁·Gy₁;

My₁=lz₁·Gz₁-lx₁·Gz₁;

Mz₁=lx₁·Gz₁-ly₁·Gx₁.

Применительно к преобразователям №2 и №6 имеем соответственно

Mx₁₂=ly₁₂·Gz₁-lz₁₂·Gy₁=ly₁₂·G·cos γ₃-lz₁₂·G·cos γ₂=0

My₁₂=lz₁₂·Gx₁-lx₁₂·Gz₁=lz₁₂·G·cos γ₁-lx₁₂·G·cos γ₃=lx₁₂·G·cosγ₃

Mz₁₂=lx₁₂·Gy₁-ly₁₂·Gx₁=lx₁₂·G·cos γ₂-ly₁₂·G·cos γ₁=lx₁₂·G·cosγ₂

Измеряемым моментом является Му₁₂.

Mx₁₆=ly₁₆·Gz₁-lz₁₆·Gy₁=ly₁₆·G·cosγ₃-lz₁₆·G·cosγ₂=lz₁₆·G·cosγ₂

My₁₆=lz₁₆·Gx₁-lx₁₆·Gz₁=lz₁₆·G·cosγ₁-lx₁₆·G·cosγ₃=lx₁₆·G·cosγ₁

Mz₁₆=lx₁₆·Gy₁-ly₁₆·Gx₁=lx₁₆·G·cosγ₂-ly₁₆·G·cosγ₁=0

Измеряемым моментом является My₁₆.

Так как моменты, создаваемые преобразователями в каждой паре, действуют в направлении относительно одной и той же оси, то суммарный момент, измеряемый преобразователями №2 и №6 по оси OY определится из выражения:

M²у₁=l² ₁₂·[(G·cosγ₃)²+(G·cosγ₁)²]=l₂·G²·(cos²γ₃+cos²γ₁)

Для преобразователей №1 и №3 соответственно получим:

x₁₁=lx₁₁=l; y₁₁=0; z₁₁=0 (преобр.№1) и x₁₃=0; y₁₃=ly₁₃=l; z₁₃=0(преобр.№3),

Mx₁₁₌ly₁₁·Gz₁-lz₁₁·Gy₁=ly₁₁·G·cosγ₃-lz₁₁·G·cosγ₂=0

My₁₁=lz₁₁·Gx₁-lx₁₁·Gz₁=lz₁₁·G·cosγ₁-lx₁₁·G·cosγ₃=lx₁₁·G·cosγ₃

Mz₁₁=lx₁₁·Gy₁-ly₁₁·Gx₁=lx₁₁·G·cosγ₂-ly₁₁·G·cosγ₁=lx₁₁·G·cosγ₂

Измеряемым моментом является М_z11.

My₁₃=ly₁₃·Gz₁-lz₁₃·Gy₁=ly₁₃·G·cosγ₃-lz₁₃·G·cosγ₂=ly₁₃·G·cosγ₃

Mx₁₃₌lz₁₃·Gx₁-lx₁₃·Gz₁=lz₁₃·G·cosγ₁-lx₁₃·G·cosγ₃=0

My₁₃=lx₁₃·Gy₁-ly₁₃·Gx₁=lx₁₃·G·cosγ₃-ly₁₃·G·cosγ₁=lx₁₃·G·cosγ₁

Измеряемым моментом является Mz_13.

Аналогично суммарный момент по направлению оси координат OZ, измеряемый преобразователями №1 и №3, будет: равен:

M²z₁=l₂·[(G·cosγ₂)²+(G·cosγ₁)²]=l²·G²·(cos²γ₂+cos²γ₁)

И, наконец, для преобразователей №4 и №5, измеряющих суммарный момент по оси координат ОХ, имеем соответственно:

x₁₄=0; у₁₄=ly₁₄=l; z₁₄=0 (преобр.№4) и x₁₅=0; y₁₅=0; z₁₅=lz₁₅=l (преобр.№5),

Mx₁₄₌ly₁₄·Gz₁-lz₁₄·Gy₁=ly₁₄·G·cosγ₃-lz₁₄·G·cosγ₂=ly₁₄·G·cosγ₃

My₁₄=lz₁₄·Gx₁-lx₁₄·Gz₁=lz₁₄·G·cosγ₁-lx₁₄·G·cosγ₃=0

Mz₁₄=lx₁₄·Gy₁-ly₁₄·Gx₁=lx₁₄·G·cosγ₂-lx₁₄·G·cosγ₁=ly₁₁·G·cosγ₁

Измеряемым моментом является Мх₁₄.

Mx₁₅₌ly₁₅·Gz₁-lz₁₅·Gy₁=ly₁₅·G·cosγ₃-lz₁₅·G·cosγ₂=lz₁₅·G·cosγ₂

My₁₅₌lz₁₅·Gx₁-lx₁₅·Gz₁=lz₁₅·G·cosγ₁-lx₁₅·G·cosγ₃=lz₁₅·G·cosγ₁

Mz₁₅=lx₁₅·Gy₁-ly₁₅·Gx₁=lx₁₅·G·cosγ₂-ly₁₅·G·cosγ₁=0

Измеряемым моментом является Mx_15/

Суммарный момент по направлению оси координат ОХ, измеряемый преобразователями №4 и №5, будет равен: M²x₁=l²·[(ly₁₄·G·cosγ₃)²+(lz₁₅·G·cosγ₂)²].

Полученные данные измерений позволяют вычислить модуль вектора G, который пропорционален механическому моменту, создаваемому всеми шестью преобразователями измерительного устройства:

где К - коэффициент преобразования устройства;

M₁ вычисляется из выражения: M₁ ²=Mx₁ ²+My₁ ²+Mz₁ ²

Итак:

M₁ ²=Mx₁₄ ²+Mx₁₅ ²+My₁₂ ²+My₁₆ ²+Mz₁₁ ²+Mz₁₃ ²=

=2·l²·G²·(cos²γ₃+cos²γ₂+cos²γ₁)

Следуя принципу «от простого - к сложному», определим все искомые величины, являющиеся нашей целью, в двух простейших случаях:

- когда оси систем координат измерителя и вектора G не рассогласованы и

- когда они рассогласованы только в горизонтальной плоскости на угол α₁.

Итак, пусть необходимо определить в этих двух случаях элементы: модуль вектора ускорения силы земного притяжения g и углы отклонения носителя измерительного устройства от горизонтальной плоскости.

Решение

где К - коэффициент преобразования измерительного канала устройства;

m - масса подвижного элемента - консольной балки, являющейся чувствительным элементом акселерометров измерительного устройства;

M₁ вычисляется из выражения: M₁ ²=Mx²+My²+Mz².

Так как: M₁ ²=Mx₁₄ ²+Mx₁₅ ²+My₁₆ ²+My₁₂ ²+Mz₁₁ ²+Mz₁₃ ²=

=2·l²·G²·[(cos²γ₃+cos²γ₂+cos²γ₁)], то для случая, когда обе системы полностью согласованы: Gy₁=0, Gx₁=0, Gz₁=G, α₁=0, β₂=0, γ₃=0, остальные углы равны 90°, т.е. когда оси Х-ов лежат в плоскости географического меридиана, выражения моментов по осям координат принимают вид: Mx₁ ²=Mx₁₄ ²+Mx₁₅ ²=K·l₁₄ ²·Gz₁ ²;

My₁ ²=My₁₆ ²+My₁₂ ²=K·l₂ ²·Gz₁ ²; M_z1 ²=Mz₁₁ ²+Mz₁₃ ²=0

M₁ ²=Mx₁ ²+My₁ ²+Mz₁ ²=2·K·l²·G².

В случае, когда системы координат рассогласованы только в плоскости XOY, то α₁=α1, β₂=α₁, γ₃=0, α₂=(90°+α₁), β₁=(90°-α₁), остальные углы равны 90°, тогда:

M₁ ²=Mx₁₄ ²+Mx₁₅ ²+My₁₆ ²+My₁₂ ²+Mz₁₁ ²+Mz₁₃ ²=

=l₁₄ ²·cos²β₂·Gz₁ ²+l₁₅ ²·cos²γ₃·Gy₁ ²+l₁₆ ²·cos²γ_3·Gx₁ ²+l₂ ²·cos²α₁·Gz₁ ²+

+l₁₁ ²·[cos(90°+α₁)·Gy₁-cosα₁·Gx₁]²+

+l₁₃ ²·[cosα₁·Gy₁+cos(90°-α₁)·Gx₁]²=2·K·l²·G².

Итак, проверка правильности вывода формулы, проведенная расчетом для двух простейших случаев, подтверждает предложенный способ и принципы его реализации.

Продолжая решение, получим:

α₁=arctg(Mx₁₄/My₁₂); Gz₁=My₁₂/sinα₁; Gy₁=My₁₅; Gx₁=My₁₆;

Направляющие косинусы

Таким образом, если направление начального ориентирования принять за ось ОХ, то направляющие косинусы определяют, соответственно, углы тангажа, крена и курса.

В рассмотренных простейших случаях результаты измерений очевидны и легко проверяемы, поэтому они и были использованы для иллюстрации работы предлагаемого устройства.

В общем случае, когда, по крайней мере, две оси не совпадают, возникает необходимость в представлении векторов в одной из систем координат, используя известные формулы координатных преобразований, исходя из того, в какой из систем желательно получить результат измерений.

Этот первый шаг позволяет составить выражения для моментов, измеряемых всеми шестью преобразователями, и, наконец, используя известные из аналитической геометрии и гравиметрии зависимости, а также характеристики измерительного устройства, вычисляют искомые величины.

Итак, нам известны характеристики измерительного устройства, такие как: коэффициент преобразования устройства - К; проекции - l всех шести чувствительных элементов преобразователей на оси системы координат устройства - OX₁Y₁Z₁; само значение массы m чувствительных элементов; G=K·M₁=K·l·m. Кроме того, из аналитической геометрии известны системы уравнений преобразования координат при переходе из одной системы координат в другую, имеющих общее начало координат и различные направления осей:

Известны соотношения, которым должны удовлетворять девять улов между осями координат при их рассогласовании:

И, наконец, в результате измерений будут получены значения моментов, измеренных всеми шестью преобразователями, что позволит вычислить, аналогично вышеприведенным простейшим случаям, искомые величины.

Анализируя признаки предлагаемого изобретения, можно выделить среди них

следующие существенные признаки, заключающиеся в том, что:

1) для измерения используется физический вектор, не изменяющий своего положения в точке измерения, независимо от того, что Земля вращается, таким вектором является вектор силы тяжести, совпадающий с вертикалью, вокруг которой все горизонтальные составляющие направлений, используемые в гироскопических устройствах, вращаются;

2) устройство измеряет одновременно не составляющие вектора силы тяжести на оси его системы координат, а проекции вектора G на координатные плоскости этой системы координат, путем измерения проекций составляющих вектора на координатные оси, а не сами составляющие;

3) измерения не требуют горизонтирования измерительного устройства;

4) такие измерения возможно реализовать только предлагаемым устройством;

5) устройство выполняет относительные измерения и потому нуждается в ориентировании устройства на начальном пункте маршрута в направлении ориентира с известными истинными азимутами;

6) устройство аналога не имеет, поскольку потребности в измерении составляющих вектора на плоскости системы координат не было, хотя элементы, используемые в устройстве, а именно лепестковые акселерометры, принцип устройства и работа которых рассматривалась выше, известны и широко применяются для измерения ускорений, что служит основой реализуемости изобретения, пополняющего арсенал средств аналогичного назначения;

7) рассматриваемое устройство содержит функционально традиционные электронные преобразовательные блоки и предлагаемый датчик, состоящий из шести идентичных однокомпонентных акселерометров, взаимное расположение которых позволяет измерять проекции составляющих вектора силы тяжести на плоскости системы координат устройства, благодаря особым свойствам, обусловленным их конструкцией, при этом каждой из трех плоскостей - двух вертикальных и одной горизонтальной - соответствует два акселерометра, измерительные оси (оси поворота) которых параллельны соответствующим осям координат, лежащим в этих плоскостях, а оси чувствительности перпендикулярны им, что иллюстрируется на фиг.3;

8) число используемых акселерометров, равное шести, является единственно возможным минимальным числом преобразователей, удовлетворяющим заданному взаимному расположению трех различных элементов на трех плоскостях, т.к. из трех элементов можно составить только одно сочетание, содержащее все три элемента: С₃₃=3!/3!(3-3)=1; в рассматриваемом случае элементом является каждая пара акселерометров, т.к. каждая из них отличается от других своим взаимным расположением, а ноль факториал равен единице (0!=1);

9) акселерометры, в зависимости от конкретных условий, можно размещать в датчике устройства произвольно, например, произвольно на горизонтальном или вертикальном основании, на нескольких плоскостях и т.п., но при этом должны соблюдаться условия: взаимное расположение акселерометров должно отвечать требованиям, изложенным выше, основание должно быть жестким и неподвижным;

10) так как преобразователи лепесткового типа имеют форму плоского «бисквита», то целесообразно с целью уменьшения габаритов устройства монтировать их на гранях основания в форме прямоугольного параллелепипеда, например куба, соблюдая при этом требования взаимного расположения, как схематически показано на фиг.6.

На основании анализа свойств предлагаемого устройства можно сделать вывод о том, что его существенными признаками являются:

использование специфических свойств акселерометров, измеряющих механические моменты относительно осей поворота, например, лепесткового или маятникового типов;

их количество и взаимное расположение, позволяющее единственным образом реализовать измерения;

минимальное, единственно возможное, количество идентичных однокомпонентных акселерометров, обеспечивающих измерение всех составляющих вектора силы тяжести на плоскости системы координат устройства;

расположение преобразователей, оси поворота которых лежат в параллельных плоскостях на противоположных гранях основания, имеющего форму параллелепипеда, размеры которого соответствуют габаритам преобразователей, а их оси чувствительности параллельны между собой и перпендикулярны плоскостям этих граней, что позволяет минимизировать габариты всего устройства в целом, при этом внутренний объем параллелепипеда может быть также использован для размещения электронного блока измерительного канала устройства.

На основании анализа существенных признаков устройства можно сделать следующие выводы:

сущность технического решения заключается в одновременном определении устройством составляющих вектора силы тяжести на координатные плоскости его системы координат, которые функционально связаны с расположением системы координат измерителя в системе координат вектора силы тяжести с искомыми параметрами;

устройство отличается количеством и совокупностью акселерометров и их взаимными связями.

Перечень фигур графических материалов

Сущность изобретения иллюстрируется графическими материалами.

Фиг.1. Принцип действия лепесткового акселерометра.

Фиг.2. Иллюстрация возможности использования вектора силы тяжести для измерения истинных азимутов лепестковым акселерометром.

Фиг.3. Размещение акселерометров, обеспечивающее измерение всех составляющих измеряемого вектора.

Фиг.4. Преобразование координат в системах, имеющих общее начало и различные направления осей.

Фиг.5. Размещение акселерометров, соответствующее существенным признакам изобретения, в совмещенных системах координат.

Фиг.6. Компоновка акселерометров, создающих момент на направление одной и той же измерительной оси.

Фиг.7. Вариант оптимального размещения акселерометров.

Исходя из выводов анализа существенных признаков устройства формула изобретения представляется в следующем ниже виде.

1. Наземный гравиметрический датчик углов истинного курса, тангажа и крена для определения истинных азимутов и углов наклона осей системы координат устройства относительно системы координат вектора силы тяжести и значение самой силы тяжести в точке измерения, содержащий шесть акселерометров лепесткового или аналогичного ему, например, так называемого маятникового типа, измеряющих механические моменты относительно осей поворота чувствительных элементов, установленных на жестком неподвижном основании таким образом, что каждой из трех плоскостей - двух вертикальных и одной горизонтальной - соответствует два акселерометра, оси поворота которых параллельны соответствующим осям координат, лежащим в этих плоскостях, а оси чувствительности перпендикулярны им.

2. Наземный гравиметрический датчик углов истинного курса, тангажа и крена по п.1, отличающийся тем, что акселерометры, оси поворота которых лежат в параллельных плоскостях, размещают на противоположных гранях общего основания, имеющего форму параллелепипеда, размеры которого соответствуют габаритам акселерометров, а их оси чувствительности параллельны между собой и перпендикулярны плоскостям этих граней, что позволяет минимизировать габариты устройства, при этом внутренний объем параллелепипеда может использоваться для размещения элементов измерительного канала.