Способ распознавания радиосигналов

Способ распознавания радиосигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к распознаванию образов, а именно - к способам распознавания радиосигналов, в частности к способам распознавания вида и параметров модуляции радиосигналов. Способ может быть использован в технических средствах распознавания радиосигналов со сложной частотно-временной структурой.

Заявленное техническое решение расширяет арсенал средств аналогичного назначения.

Известен способ распознавания сигналов [Асеев А.Ю., Балаболин О.В., Григорьев С.В., Сауков А.М. Патент РФ №2133501 по заявке №98102689 А2, кл. 5 G 06 К 9/00, от 04.02.98], заключающийся в сравнении на выборке длиной Q канальных символов "скользящим окном" всех комбинаций длиной К друг с другом, где К/2 - предполагаемая память помехоустойчивого сверточного кодера, и последующем подсчете частоты появления событий, заключающихся в том, что в двух отрезках кодовой последовательности имеется единственная пара несовпадающих символов, и эти символы одновременно не принадлежат двум различным подансамблям разбиения.

Недостатком этого способа является узкая область его применения, т.к. при его использовании возможно распознавание лишь сигналов, сформированных на основе сигнально-кодовых конструкций.

Известен также способ распознавания сигналов [Омельченко В.А. Распознавание сигналов по спектру мощности в оптимальном базисе Карунена-Лоева. - Известия ВУЗов MB и ССО СССР. Сер. Радиоэлектроника, 1980, №12, С.11-18.], при котором вычисляют энергетический спектр сигнала, затем выполняют над ним преобразование Карунена-Лоэва и на основе полученных признаков сначала производят селекцию сигналов на полезные и мешающие, а затем, в случае полезного сигнала осуществляют его сравнение с имеющимися эталонными классами и отнесение к одному из них.

Недостатком данного способа является низкая вероятность правильного распознавания¹ (¹Вероятность правильного распознавания - относительная частота принятия правильного решения при отнесении принятого радиосигнала к одному из эталонных классов. События правильного распознавания является противоположным (дополнительным) к событию ошибочного распознавания (Р_расп=1-Р_ош) - см. Дж. Ту, Р.Гонсалес. Принципы распознавания образов. Пер. с англ. - М.: Мир, 1978. - стр.142-152.) сигналов, имеющих похожие спектры, что обусловлено низкой контрастностью сформированных признаков распознавания.

Наиболее близким по технической сущности к заявленному является способ распознавания радиосигналов на основе сингулярного разложения псевдо-частотно-временного распределения (псевдо-ЧВР) Вигнера-Вилле [N. M. Marinovic, G. Eichmann. An expansion of Wigner distribution and its applications. - Proc. IEEE ICASSP-85, 1985, pp.1021-1024]. В указанном способе-прототипе предварительно на основе псевдо-ЧВР Вигнера формируют матрицы распределения энергии (РЭ) эталонных радиосигналов, выполняют их спектральное разложение, формируют параметры эталонных радиосигналов, затем принимают распознаваемый радиосигнал, дискретизируют и квантуют его, формируют матрицу распределения энергии принятого радиосигнала, выделяют признаки принятого радиосигнала, сравнивают их с параметрами эталонных радиосигналов и по результатам сравнения идентифицируют принятый радиосигнал.

Недостатком прототипа является низкая достоверность распознавания радиосигналов сложной частотно-временной структуры, а также радиосигналов при воздействии на них шумов и помех, что обусловлено особенностями используемого для распознавания псевдо-ЧВР Вигнера-Вилле [Коэн Л. Время-частотные распределения. Обзор //ТИИЭР, 1989, т. 77, №10. С.72-121]. Снижение достоверности распознавания происходит вследствие появления интерференционного фона и ложных пиков мощности в псевдо-ЧВР Вигнера-Вилле, искажающих реальную картину распределения энергии сигнала в координатах частота-время.

Целью заявленного технического решения является разработка способа распознавания радиосигналов, обеспечивающего повышение достоверности распознавания сигналов сложной структуры, за счет устранения в формируемой матрице РЭ сигнала в координатах частота-время интерференционного фона и ложных пиков энергии для многокомпонентных и зашумленных сигналов (т.е. при малом отношении сигнал-шум (ОСШ)) с сохранением при этом необходимого частотного и временного разрешения, а также сокращение длительности процесса распознавания за счет уменьшения времени формирования матрицы РЭ.

Поставленная цель достигается тем, что в известном способе распознавания сигналов радиоэлектронных средств, заключающемся в том, что предварительно формируют матрицы РЭ эталонных радиосигналов, выполняют их спектральное разложение, формируют параметры эталонных радиосигналов, затем принимают распознаваемый радиосигнал, дискретизируют и квантуют его, формируют матрицу РЭ принятого радиосигнала, выявляют признаки принятого радиосигнала, сравнивают их с параметрами эталонных радиосигналов и по результатам сравнения идентифицируют принятый радиосигнал, в заявленном способе для формирования матрицы РЭ эталонных радиосигналов вычисляют непрерывное вейвлет-преобразование (НВП). Затем из каждой матрицы РЭ формируют векторы РЭ эталонных радиосигналов. После чего для всех полученных векторов РЭ вычисляют общую ковариационную матрицу. Спектральное разложение матриц РЭ эталонных сигналов выполняют путем вычисления матрицы собственных значений и матрицы собственных векторов общей ковариационной матрицы. Затем формируют усеченную матрицу собственных векторов, включающую лишь собственные векторы, соответствующие максимальным собственным значениям ковариационной матрицы. Для формирования параметров эталонных радиосигналов умножают усеченную матрицу собственных векторов на векторы РЭ эталонных радиосигналов, а результаты вычислений усредняют и используют в качестве параметров эталонных радиосигналов. Причем для формирования матрицы РЭ принятого радиосигнала вычисляют НВП, и формируют из полученной матрицы вектор РЭ принятого радиосигнала. Затем умножают усеченную матрицу собственных векторов на вектор РЭ принятого радиосигнала. Результаты вычислений принимают в качестве признаков распознавания принятого радиосигнала.

Благодаря новой совокупности существенных признаков в заявленном способе распознавания радиосигналов за счет применения НВП обеспечивается полное устранение интерференционного фона и ложных пиков энергии в формируемой матрице РЭ сигнала с сохранением необходимого частотного и временного разрешения, что приводит к повышению достоверности распознавания многокомпонентных и зашумленных радиосигналов, а также к сокращению продолжительности процесса распознавания вследствие того, что вычисление матрицы РЭ сигнала на основе НВП требует меньших вычислительных затрат, чем на основе псевдо-ЧВР.

Проведенный анализ уровня существующей техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, которые тождественны всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности "новизна". Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности "изобретательский уровень".

Заявленный способ поясняется чертежами, на которых показаны:

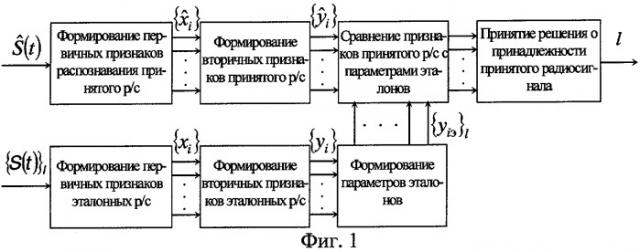
фиг.1. Обобщенная структурная схема процесса распознавания;

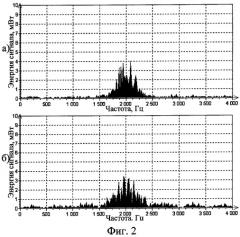
фиг.2. Спектры сигналов ММС (а) и ФМ2 (б);

фиг.3. РЭ суммы двух гармонических сигналов, вычисленное на основе псевдо-ЧВР Вигнера-Вилле;

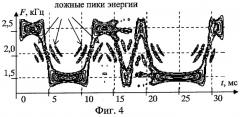
фиг.4. РЭ тестового сигнала ЧМ2 на основе псевдо-ЧВР Вигнера-Вилле;

фиг.5. РЭ тестового сигнала линейной частотной модуляции на основе псевдо-ЧВР Вигнера-Вилле;

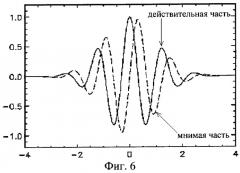
фиг.6. График действительной и мнимой частей вейвлета Морле;

фиг.7. РЭ сигнала ЧМ2 на основе НВП Морле 5-го порядка;

фиг.8. Сравнение перечня операций, необходимых для формирования матрицы РЭ сигнала на основе псевдо-ЧВР Вигнера-Вилле и на основе НВП Морле;

фиг.9. Структурная схема заявленного способа распознавания;

фиг.10. Обобщенный график зависимости вероятности правильного распознавания от ОСШ.

В общем случае процесс распознавания включает в себя следующие процедуры (фиг.1): измерение первичных признаков {x_i}_l для каждого эталонного радиосигнала из множества {S(t)}_l, формирование на их основе вторичных признаков {y_i}_l и формирование на их основе параметров эталонных радиосигналов {у_iэ}_l, которые затем сравнивают с признаками принятого радиосигнала и принимают решение об отнесении принятого радиосигнала к одному из L эталонных классов.

Важным условием для повышения достоверности распознавания является выбор признаков распознавания. Преимущества выбора НВП для формирования признаков распознавания радиосигналов можно обосновать следующим образом.

При распознавании радиосигналов использование только временной или частотной информации о сигнале часто не позволяет сформировать контрастные признаки для многих сигналов. Например, известно, что энергетические спектры сигналов с минимальным частотным сдвигом (ММС) и двойной фазовой манипуляции (ФМ2) практически неразличимы при одинаковых скоростях манипуляции. На фиг.2 показаны спектры этих сигналов при манипуляционной скорости 500 Бод.

Выявить необходимые для распознавания различия радиосигналов позволяет их представление одновременно во временной и частотной областях. В ряде случаев, примененное в способе-прототипе псевдо-ЧВР Вигнера-Вилле позволяет качественно решать задачи распознавания радиосигналов, так как с высокой точностью отражает их частотные и временные параметры. Вместе с тем, существенным недостатком ЧВР является появление в них интерференционного фона и ложных пиков энергии при анализе многокомпонентных или совокупности нескольких сигналов, а также при воздействии шумов и помех. Они искажают реальную картину распределения энергии сигнала в координатах частота-время и существенно ухудшают результаты распознавания. Причем применение различных видов сглаживания (псевдо-ЧВР) полностью этих проблем не решает. На фиг.3 показан вид псевдо-ЧВР Вигнера-Вилле для двух гармонических сигналов с частотами f₁ и f₂. Между ними наблюдается интерференционный фон. На фиг.4 показана матрица РЭ сигнала двухпозиционной частотной манипуляции (ЧМ2), где видно, что в РЭ энергия присутствует там, где наличие ее не ожидалось. Лишь для сигналов с относительно простой частотно-временной структурой, например, сигналов линейной частотной модуляции, сформированных на основе псевдо-ЧВР Вигнера-Вилле, интерференционный фон и ложные пики энергии отсутствуют (фиг.5) [Коэн Л. Время-частотные распределения. Обзор //ТИИЭР, 1989, т. 77, №10, С.72-121].

Таким образом, примененное в способе-прототипе псевдо-ЧВР Вигнера-Вилле в полной мере не позволяет воспользоваться своими положительными свойствами по локализации энергии в плоскости частота-время в случае анализа многокомпонентных сигналов (фиг.4) в связи с возникновением интерференционного фона ЧВР [Алексеев А.А., Кириллов А.Б. Технический анализ сигналов и распознавание радиоизлучений. - СПб.: ВАС, 1998, 368 с.]. Кроме этого, распознавание по способу-прототипу занимает значительное время, что связано с вычислительной сложностью формирования матрицы РЭ на основе псевдо-ЧВР Вигнера-Вилле.

Для повышения качества формирования первичных признаков распознавания радиосигналов, с использованием матриц РЭ радиосигналов, необходимо устранить в них интерференционный фон и ложные пики энергии с сохранением необходимого частотного и временного разрешения. Добиться этого можно за счет адаптации ширины временного окна к частоте анализа в спектрограмме. Из теории анализа сигналов известно [Алексеев А.А., Кириллов А.Б. Технический анализ сигналов и распознавание радиоизлучений. - СПб.: ВАС, 1998, 368 с.], что для получения с достаточной точностью информации о высокочастотных спектральных составляющих сигнала важно извлекать ее из относительно малых временных интервалов. Информацию о низкочастотных спектральных составляющих сигнала можно извлекать из относительно широких временных интервалов, выигрывая при этом в частотном разрешении. Именно такой принцип лежит в основе вейвлет-анализа.

Наиболее близкий к описанному выше подходу результат дает НВП, которое определяется как интегральное значение скалярного произведения сигнала S(t) на вейвлет-функцию

заданного вида:

где а - переменная, определяющая масштаб вейвлета (является аналогом частоты в анализе Фурье); b - переменная, определяющая величину сдвига (по времени) вейвлета.

Как правило, в качестве вейвлет-функций берутся непериодические, локализованные по частоте и по времени функции, например функции, имеющие один или два близко расположенных глобальных экстремума и быстро затухающие [Дьяконов В. MATLAB. Обработка сигналов и изображений. Специальный справочник. - СПб.: Питер, 2002. 608 с.].

В псевдо-ЧВР Вигнера, примененном в способе-прототипе, для разложения входных сигналов используются гармонические базисные функции. В результате получены приемлемые показатели эффективности распознавания, за исключением уже отмеченных выше недостатков. В предлагаемом способе, для получения в каждом частотном канале результатов анализа, близких к прототипу, в качестве базисного вейвлета выбран вейвлет Морле, который представляет комплексную синусоиду, ограниченную колоколообразной гауссовой функцией [Дьяконов В. MATLAB. Обработка сигналов и изображений. Специальный справочник. - СПб.: Питер, 2002. 608 с.]:

Здесь u - значение, определяющее число осцилляции (базовую ширину) вейвлета. Внешний вид мнимой и действительной частей вейвлета Морле представлен на фиг.6. РЭ фрагмента тестового сигнала ЧМ2, вычисленное на основе НВП Морле, представлено на фиг.7.

Анализ результатов НВП, приведенных на фиг.7, показывает, что сигнальные составляющие хорошо локализованы по времени и частоте, нет ложных пиков энергии и интерференционного фона. Таким образом, для формирования первичных признаков распознавания радиосигналов целесообразно применять НВП на основе вейвлета Морле.

Уменьшение вычислительной сложности процедуры формирования матрицы РЭ сигнала при использовании НВП по сравнению с псевдо-ЧВР (фиг.8) объясняется следующим. При формировании матрицы сигнала на основе псевдо-ЧВР Вигнера сигнал дискретизируют, формируют выборку дискретных отсчетов, вычисляют аналитический сигнал для выборки, выполняют умножение аналитического сигнала на комплексно-сопряженный к нему и сдвинутый во времени, умножают результат на функцию "окна", выполняют преобразование Фурье и формируют столбец матрицы псевдо-ЧВР (см.фиг.8, операции 1.1-1.8). При формировании матрицы РЭ сигнала на основе НВП сначала выбирают масштаб вейвлет-функции для построения одного столбца матрицы РЭ сигнала, а затем выполняют свертку сигнала с масштабированными и сдвинутыми во времени копиями вейвлет-функции и формируют из результатов столбец матрицы РЭ сигнала. При этом для выполнения одной свертки сигнала с вейвлет-функцией (фиг.8, операция 2.3) необходимо выполнить всего k элементарных операций умножения и сложения, где k - длина вейвлет-фильтра, причем k по определению всегда много меньше длины анализируемого сигнала, т.е. требуется значительно меньше операций, чем для выполнения одного умножения сигнала на его комплексно-сопряженную копию, т.к. длина вейвлет-функции мала по определению (фиг.8, операция 1.4). Однако дополнительно, при свертке сигнала с вейвлет-функцией необходимо выполнить k элементарных операций сложения, т.е. имеет место приближенно одинаковое время выполнения операций 1.4 и 2.3. Таким образом, применение НВП по сравнению с псевдо-ЧВР при построении каждой строки (столбца) матрицы сигнала позволяет исключить операции 1.3, 1.5, и 1.6 (фиг.8) и, тем самьм, сократить время формирования матрицы сигнала.

Суть заявленного способа заключается в следующем (фиг.9).

Предварительно путем вычисления НВП формируют совокупность матриц РЭ {K_ν}_l эталонных радиосигналов S_l, где l=1,..., L, L - количество эталонных классов. Далее формируют из них совокупность векторов РЭ эталонных радиосигналов причем каждый вектор формируют путем последовательной записи столбцов матрицы К один под другим. После чего рассчитывают для всех векторов РЭ эталонных радиосигналов общую ковариационную матрицу М и вычисляют для нее матрицу собственных значений и матрицу собственных векторов А. Затем из полученной матрицы собственных векторов А формируют усеченную матрицу собственных векторов включающую лишь те собственные векторы, которые соответствуют максимальным собственным значениям общей ковариационной матрицы М, количество которых выбирают так, чтобы их сумма составляла не менее 80% от следа матрицы собственных значений . Далее формируют параметры Θ_l эталонных радиосигналов S_l. В качестве параметров эталонов используют матрицу средних от произведений усеченной матрицы собственных векторов на векторы РЭ эталонного радиосигнала

Затем формируют признаки принятого радиосигнала . В качестве признаков принятого радиосигнала используют произведение усеченной матрицы собственных векторов на вектор РЭ принятого радиосигнала

Причем вектор РЭ принятого радиосигнала формируют из матрицы РЭ вычисленной на основе НВП. По результатам сравнения эталонных описаний и признаков радиосигнала принимают решение об отнесении его к одному из эталонных классов.

Рассмотрим подробно каждый из этапов распознавания радиосигналов заявленным способом.

Предварительно формируют перечень распознаваемых классов сигналов и создают для них эталонные описания, для чего системе распознавания предъявляют классифицированные последовательности дискретных отсчетов (z₀, z₁, z₂,... z_m)_l эталонных радиосигналов S_l, где m - длина последовательности эталонного радиосигнала, 1=1,2,... L - номер эталона, L - общее количество эталонов. Величина m определяется из условия m≥100·N, где N - длина выборки. Число 100 определяет минимально допустимое количество выборок для получения состоятельных статистических оценок и получено экспериментально. Хотя рекомендуемое количество выборок больше 200, однако, на практике часто ограничиваются меньшим числом, допуская при этом определенный проигрыш в точности вычисления статистических оценок [Математический энциклопедический словарь. М.: Сов. Энциклопедия, 1988. 847 с.].

Далее из каждой эталонной последовательности S_l формируют выборок [s₀,s₁,s₂,...S_N-1)_l,ν, где - номер выборки (операция формирования выборок известна и описана, например в [Г.Корн, Т.Корн. Справочник по математике. Пер. с англ. - М.: Наука, 1977, стр.638-643]. Длина выборки N выбирается в пределах 256...16000, в зависимости от требований по вероятности правильного распознавания и времени обработки. Чем больше N, тем выше вероятность правильного распознавания, но время обработки возрастает. Выборки формируют следующим образом. В качестве первой выборки берут первые N отсчетов эталонной последовательности: [s₀,s₁,s₂,...s_N-1)_l=[z₀,z₁,z₂,...z_N-1). В качестве второй выборки берут следующие N отсчетов эталонной последовательности: [s₀,s₁,s₂,...s_N-1)₂=[z_N,z_N+1,z_N+2,...z_2N-1). В качестве третьей выборки берут третьи N отсчетов эталонной последовательности [s₀,s₁,s₂,...s_N-1)₃=[z_2N,z_2N+1,z_2N+2,...z_3N-1) и т.д. до последней выборки т.е. до окончания эталонной последовательности.

После этого, на основе НВП полученных выборок [s₀,s₁,s₂,...S_N-1)_l,ν формируют совокупность матриц РЭ {К_ν}_l эталонных сигналов. Порядок формирования матрицы РЭ К сигнала известен как алгоритм НВП и описан, например в [Дьяконов В. MATLAB. Обработка сигналов и изображений. Специальный справочник. - СПб.: Питер, 2002. 608 с. С.307-312; Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для вузов по спец. «Радиотехника». - 3 изд., перераб. и доп. - М.: Выш. шк., 2000. 462 с., С.65-68] и заключается в следующем. Значения элементов К-k_a,b матрицы вычисляют в соответствии с выражением

где a,b∈R. Это выражение является дискретной формой выражения (1). При этом:

где при использовании в качестве базисного вейвлета функции Морле используют дискретный вариант выражения (2) при u=5:

Далее из совокупности матриц РЭ {К_ν}_l эталонных радиосигналов формируют совокупность векторов РЭ эталонных радиосигналов, причем каждый вектор формируют путем последовательной записи столбцов матрицы К один под другим. Затем из полученных векторов эталонных сигналов формируют обобщенную ковариационную матрицу М. Процесс формирования обобщенной ковариационной матрицы известен и описан, например, в [Фукунага К. Введение в статистическую теорию распознавания образов. Пер. с англ. - М.: Наука., 1979. 368 с., С.245-247; Сборник научных программ на Фортране. Вып.1. Статистика. Нью-Йорк, 1960-1970, пер. с англ. (США). М., Статистика, 1974. 316 с., С.80-83].

Затем вычисляют матрицу собственных векторов А и матрицу собственных значений , на главной диагонали которой находятся собственные значения матрицы М-(λ₀,λ₁,λ₂,...λ_n-1)=diag(Ξ). Процедура вычисления собственных значений и собственных векторов матриц известна и подробно описана, например, в [Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра. Пер. с англ. - М.: Машиностроение, 1976. - 117 с.; Сборник научных программ на Фортране. Вып.2. Матричная алгебра и линейная алгебра. Нью-Йорк, 1960-1971, пер. с англ. (США). М., Статистика, 1974. 224 с., С.187-210].

После этого из полученных собственных значений выбирают некоторое количество максимальных так, чтобы их сумма составляла не менее 80% от суммы всех собственных значений. Затем из полученной матрицы собственных векторов А формируют усеченную матрицу собственных векторов оставляя в ней лишь те собственные векторы, которые соответствуют отобранным максимальным собственным значениям.

Далее формируют параметры {Θ_l} эталонных радиосигналов {S₁}, в качестве которых используют матрицу средних от произведений усеченной матрицы собственных векторов на векторы РЭ радиосигнала:

Процедура вычисления матрицы средних известна и описана, например, в [Сборник научных программ на Фортране. Вып.1. Статистика. Нью-Йорк, 1960-1970, пер. с англ. (США). М., Статистика, 1974. 316 с., С.38-48].

После этого переходят к распознаванию радиосигналов. Сначала принятый радиосигнал дискретизируют по времени и квантуют по напряжению (операция дискретизации и квантования сигналов известна и описана, например, в [В.А. Григорьев. Передача сигналов в зарубежных информационно-технических системах. - СПб.: ВАС. 1998. стр.83-85]). Затем из совокупности дискретных отсчетов {z_i} радиосигнала так же как было описано выше, выделяют выборку {s₀,s₁,s₂,...s_m-1} длиной m: [s₀,s₁,s₂,...s_m-1)_l=[z₀,z₁,z₂,...z_m-1). На основе этой выборки формируют матрицу РЭ принятого радиосигнала с применением НВП согласно выражениям (3, 4, 5). Далее формируется вектор РЭ принятого сигнала путем последовательной записи столбцов матрицы один под другим.

Затем формируют признаки принятого радиосигнала В качестве признаков принятого радиосигнала используют произведение усеченной матрицы собственных векторов на вектор РЭ принятого радиосигнала:

И в заключение на основе сравнения признаков принятого радиосигнала с параметрами эталонных радиосигналов принимают решение об отнесении принятого радиосигнала к одному из эталонных классов, с использованием одного из решающих правил. Процедуры принятия решения являются известными и описаны, например, в [Я.А.Фомин, Г.Р.Тарловский. Статистическая теория распознавания образов. - М.: Радио и связь, 1986, стр.30-46].

Сравнительная оценка вероятности правильного распознавания Р_расп с помощью заявленного способа и способа-прототипа выполнена путем моделирования процесса распознавания на ЭВМ.

В качестве распознаваемых сигналов использованы 7 моделей сигналов амплитудной, частотной и фазовой телеграфии, с различными скоростями передачи (AT 50 Бод - радиосигнал амплитудной телеграфии со скоростью передачи 50 Бод; ЧТ 800 Гц 500 Бод, ЧТ 800 Гц 200 Бод, ЧТ 600 Гц 100 Бод, ЧТ 200 Гц 100 Бод - радиосигналы частотной телеграфии с разносом 800, 600, 200 Гц и скоростью передачи 500, 200, 100 Бод; ФТ 500 Бод, ФТ 1200 Бод - радиосигналы фазовой телеграфии со скоростью передачи 500 и 1200 Бод). Радиосигналы нормированы относительно уровня средней мощности. Формирование параметров эталонов проводили по 100 выборкам каждого сигнала. Вероятность правильного распознавания оценивали методом Монте-Карло по 100 выборкам для каждого сигнала при значениях ОСШ по мощности, т.е. P_c/P_ш, - 0÷20 дБ (фиг.10).

Результаты сравнительных расчетов показали:

1. вероятность правильного распознавания радиосигналов заявленным способом выше, чем способом-прототипом (фиг.10):

- в области низких (0÷2 дБ) значений Р_с/Р_ш - в 1.1-1.3 раза;

- в области средних (2÷8 дБ) значений Р_с/Р_ш - в 2-3 раза;

- в области высоких (более 8 дБ) значений Р_с/Р_ш - в 1.1-1.2 раза;

2. продолжительность процедуры распознавания при применении заявленного способа в среднем в 6-8 раз меньше, чем при использовании способа-прототипа.

Способ распознавания радиосигналов, заключающийся в том, что предварительно формируют матрицы распределения энергии эталонных радиосигналов, выполняют их спектральное разложение, формируют параметры эталонных радиосигналов, затем принимают распознаваемый радиосигнал, дискретизируют и квантуют его, формируют матрицу распределения энергии принятого радиосигнала, выделяют признаки принятого радиосигнала, сравнивают их с параметрами эталонных радиосигналов и по результатам сравнения идентифицируют принятый радиосигнал, отличающийся тем, что для формирования матрицы распределения энергии эталонных радиосигналов вычисляют непрерывное вейвлет-преобразование последовательности дискретных квантованных отсчетов эталонных радиосигналов, затем для каждой матрицы формируют векторы распределения энергии, после чего вычисляют для всех векторов распределения энергии эталонных радиосигналов общую ковариационную матрицу, а спектральное разложение матриц распределения энергии эталонных радиосигналов выполняют путем вычисления собственных векторов и собственных значений общей ковариационной матрицы, формируют усеченную матрицу собственных векторов путем выбора собственных векторов общей ковариационной матрицы, соответствующих ее максимальным собственным значениям, а при формировании параметров эталонных радиосигналов умножают усеченную матрицу собственных векторов на векторы распределения энергии эталонных радиосигналов, а в качестве параметров эталонов используют средние значения полученных произведений, причем для формирования матрицы распределения энергии принятого радиосигнала вычисляют непрерывное вейвлет-преобразование последовательности дискретных квантованных отсчетов распознаваемого радиосигнала, затем из сформированной матрицы распределения энергии принятого радиосигнала формируют вектор распределения энергии, а для выделения признаков принятого радиосигнала умножают усеченную матрицу собственных векторов на вектор распределения энергии и результаты вычислений принимают в качестве признаков распознавания принятого радиосигнала.