Трехфазная двухслойная дробная (q=5,5) полюсопереключаемая в отношении 2p1/2p2=2/1 обмотка

Трехфазная двухслойная дробная (q=5,5) полюсопереключаемая в отношении 2p1/2p2=2/1 обмотка

Иллюстрации

Показать все

Реферат

Изобретение относится к трехфазным полюсопереключаемым в отношении 2:1 обмоткам (ППО) электрических машин переменного тока и может использоваться на статоре трехфазных двух- и многоскоростных асинхронных двигателей (АД) с короткозамкнутым ротором.

Известны петлевые двухслойные симметричные m=3-фазные ППО с числами полюсов в отношении 2p₁/2p₂=2/1 со схемами соединения фаз Y/YY или Δ/YY, выполняемые в z пазах из N_кг=6р₂ катушечных групп с q=z/6p₂ катушками в каждой при их шаге по пазам y_п≈z/2р₁ и разделении каждой фазы на две одинаковые части с нечетными группами в одной и четными в другой с дополнительными выводами средних точек в каждой фазе, где q - целое число [Сергеев П.С. и др. Проектирование электрических машин. М.: Энергия, 1970, с.450-451]. При дробном числе q=z/6p₂=b+0,5 (b=1, 2, 3,...) m=3-фазные обмотки имеют неодинаковые чередующиеся большие (b+1) - катушечные и малые b-катушечные группы [Вольдек А.И. Электрические машины. Л.: Энергия, 1978, с.409-411], что не позволяет выполнять их в качестве таких симметричных ППО.

В изобретении ставится задача выравнивания ЭДС и сопротивлений больших и малых катушечных групп m=3-фазной дробной обмотки при q=5,5, что позволяет выполнять ее в качестве симметричной ППО с числами полюсов 2p₁/2p₂=4/2, 8/4, 12/6.

Решение поставленной задачи достигается тем, что для трехфазной двухслойной дробной (q=5,5) полюсопереключаемой в отношении 2p_l/2p₂=2/1 обмотки с соединением фаз по схемам Y/YY или Δ/YY, выполняемой в z=6p₂q пазах из N_кг=6p₂ катушечных групп с шагом катушек по пазам У_п≈z/2p₁ при разделении каждой фазы на две части с нечетными группами в одной, четными в другой и с дополнительными выводами средних точек в каждой фазе: при 2p_l/2p₂=4/2, 8/4, 12/6 полюсах, g=5,5 концентрические группы нечетные шестикатушечные имеют шаги катушек у_пi=13-2(i-1) с числами витков (1-x)w_к катушек с i=1, 6 и (1+x)w_к катушки с i=3, а четные пятикатушечные - у^' _пi=12-2(i-1) с числом витков (1+х)w_к катушки с i=3 при w_к витках остальных катушек групп, где z=33 для 2p_l/2p₂=4/2, z=66 для 2p₁/2p₂=8/4, z=99 для 2p₁/2p₂=12/6, i=1...6 - номер катушки в группе, начиная с наружной, 2w_к - число витков каждого паза при значении х=0,52.

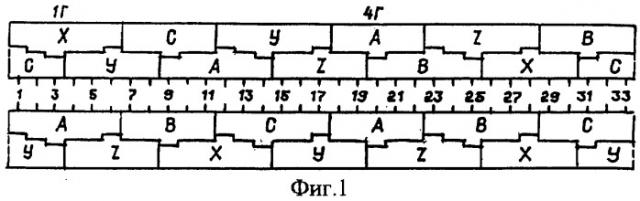
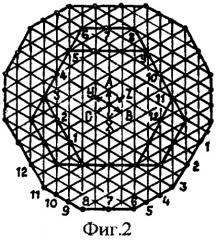
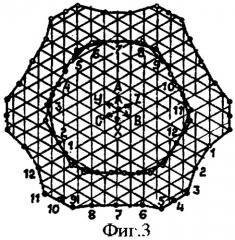
На фиг.1 показаны развертки пазовых слоев предлагаемой двухслойной трехфазной обмотки при 2р₁/2р₂=4/2, q=5,5 и z=33 пазах с номерами 1...33, N_кг=6 катушечных группах с номерами 1Г...6Г: сверху - для полюсности 2р₂=2 с чередованиями фазных зон в последовательности A-Z-B-X-C-Y, где пронумерованы группы 1Г, 4Г первой фазы, и снизу - для полюсности 2р₁=4 с чередованиями фазных зон в последовательности А-В-С для верхнего и X, Y, Z нижнего слоя; на фиг.2 и 3 построены (по треугольной сетке) многоугольники МДС обмотки по фиг.1 для полюсностей 2p₂=2 (наружные) и 2p₁=4 (внутренние) при катушках равно-(фиг.2) и неравновитковых (фиг.3) для х=0,5. ППО для 2p₁/2p₂=8/4 (z=66) и 2p₁/2p₂=12/6 (z=99) повторяют параметры обмотки по фиг.1 при ее повторе два и три раза.

Соединения фаз, например Y/YY для ППО при 2p₁/2p₂=8/4 полюсах соответствуют: Y - для полюсности 2p₁=8 с выводами начал фаз а, b, с при последовательно-согласном включении в каждой фазе нечетных групп в одной части и четных в другой с дополнительными выводами (а', b', с') из их средних точек (например, в фазе а группы 1Г, 7Г, 10Г, 4Г с дополнительным выводом а^' из конца 7Г и начала 10Г), поэтому ППО для 2p₁=8 имеет m'=m=3 фазные зоны на пару полюсов с чередованиями по нижней развертке фиг.1; YY - для 2p₂=4 с выводами а', b', с' (выводы а, b, с закорочены) при параллельно-встречном включении тех же групп (например, в фазе а' - группы 10Г, 4Г и -7Г, -1Г), поэтому ППО для 2р₂=4 имеет m'=2m=6 фазных зон на пару полюсов с чередованиями по верхней развертке фиг.1 с зонами A-Z-B-X-C-Y (начиная с группы 4Г).

Обмотка по фиг.1 для шестикатушечных групп (нечетных) имеет шаги катушек по пазам y_пi=13-2(i-1)=13, 11, 9, 7, 5, 3 (y_к.cp=z/2p_l-0,25=8) с числами витков (1-x)w_к катушек с i=1, 6 и (1+х)w_к катушки с i=3, а для пятикатушечных групп (четных) - y^' _пi=12-2(i-1)=12, 10, 8, 6, 4 с числом витков (1+х)w_к катушки с i=3 при w_к витках в остальных катушках групп, где значение "х" определяется из условия получения одинаковых ЭДС больших и малых групп для полюсности 2р₂, соответствующей ее соединению YY. По коэффициентам укорочения K_yi=sin(90°У_пi/τ_n) катушек для каждой полюсности определяются ЭДС Е_г больших, малых катушечных групп при полюсном делении τ_п=z/2p и 2w_к=2 витках паза: для 2p₁=4 при τ_п=z/2p₁=8,25-K_yi=(1-x)0,618159(y_пi=13), 0,86603(у_пi=11), (1+х)0,989821(у_пi=9), 0,971812 (y_пi=7), 0,81458 (у_пi=5), (1-x)0,540641 (у_пi=3) и E_г.б=Σ(K_yiW_ki)=4,8010339-х0,16898 - для групп больших (нечетных), К_уi=0,75575 (у^' _пi=12), 0,945001 (У^' _пi=10), (1+х)0,998867 (у^' _пi=8), 0,909632 (у^' _пi=6), 0,690079 (у^' _пi=4) и Е_г.м=4,299329+х0,99887 - для групп малых (четных) и обмоточный коэффициент для полюсности 2p₁ равен

для 2р₂=2 при τ_п=z/2p₂=16,5-К_уi=(1-х)0,945008 (у_пi=13), 0,86603 (y_пi=ll), (1+х)0,75575 (у_пi=9), 0,618159 (у_пi=7),0,458227 (у_пi=5), (1-х)0,281733 (у_пi=3) и Е_г.б=3,92490-х0,47099 - для групп больших, K_yi=0,909632 (у'_пi=12), 0,814576 (У'_пi=10), (1+х)0,690079 (у^' _пi=8), 0,540641 (у^' _пi=6), 0,371663 (у'_пi=4) и Е_г.м=3,326591+х0,690079 - для малых групп и из условия Е_г.б=Е_г.м определяется значение х=0,52; К_об.р2 для полюсности 2р₂ равен

а средний шаг катушек при х=0,52 равен У_п.ср=Σ(у_пiw_ki)11=8-8x/11=7,622.

Суммарные шаги у_г.б и у_г.м больших и малых групп при х=0,52 равны у_г.б=48-7х=44,36, y_г.м=40+8x=44,16, т.е. практически одинаковы, поэтому практически одинаковы и сопротивления (активные и индуктивные рассеяния) больших и малых групп.

Таким образом, предлагаемая неравновитковая обмотка по фиг.1 при х=0,52 имеет одинаковые ЭДС, сопротивления для 2р₂ всех групп, что обеспечивает симметрию ППО для полюсности 2р₂ при соединении в YY.

Из многоугольников МДС фиг.2 и 3 по соотношениям

определяется для каждой полюсности ППО коэффициент дифференциального рассеяния σ_д, характеризующий качество обмотки по гармоническому составу ее МДС, где R_Д ² - квадрат среднего радиуса j=1...2q пазовых точек относительно центра многоугольника и R_o - радиус окружности для основной гармонической МДС [Попов В.И. Определение и оптимизация параметров трехфазных обмоток по многоугольникам МДС//Электричество, 1997, №9, с.53-55].

Из многоугольников МДС фиг.2, 3 по (1)-(3) при стороне сетки в единицу длины для х=0 и х=0,5 по теореме косинусов определяются:

для 2р₂ при х=0 (фиг.2) - R_д ²=Σ(R_j ²)/11=531/11, R_o=33·0,65923/π, σ_д%=0,67 и при х=0,52(фиг.3) - R² _д=(531+30х+9x²)/11, R_o=33·0,6696/π и σ_д%=0,89, т.е. σ_д.р2 возрастает в 0,89/0,67=1,33 раза;

для 2p₁ при х=0 (фиг.2) - R_Д ²=215/11, R_o=33·0,8273/2π и σ_Д%=3,53; при х=0,52 (фиг.3) - R² _д=(215+22x+17x²)/11, R_o=33·0,86654/2π, σ_Д%=1,40 и значение σ_д.р1 снижается в 3,53/1,40=2,52 раза.

Если эффективность неравновитковой ППО по фиг.1 оценивать произведениями ее коэффициентов обмоточных по (1)-(2) и дифференциального рассеяния по (3), то при х=0,52 коэффициент ее эффективности равен К_эф=(0,6696·0,8665/0,6592·0,8273)(0,67·3,53/0,89·1,40)=2,02, что характеризует высокую степень эффективности предлагаемой обмотки.

Таким образом, предложенная неравновитковая ППО по фиг.1 при х=0,52 характеризуется полной ее симметрией для полюсностей 2p₁ и 2р₂, имеет высокие обмоточные коэффициенты и пониженное дифференциальное рассеяние σ_д.р1 для большей полюсности 2p₁. Значение показателя "х" неравновитковости катушек при реальном проектировании трехфазного АД с такой ППО может отличаться от найденного значения х=0,52 на ±(2...3)%. Равновитковая (х=0) ППО при q=5,5 имеет ухудшенные электромагнитные параметры из-за ее несимметричности для полюсности 2р₂ (с соединением в двойную звезду YY) и наличия уравнительных токов.

Трехфазная двухслойная дробная (q=5,5) полюсопереключаемая в отношении 2p₁/2p₂=2/1 обмотка с соединением фаз по схеме Y/YY или Δ/YY, выполняемая в z=6p₂q пазах из N_кг=6р₂ катушечных групп с шагом катушек по пазам у_п≈z/2p₁ при разделении каждой фазы на две части с нечетными группами в одной, четными в другой и с дополнительными выводами средних точек в каждой фазе, отличающаяся тем, что при 2p₁/2p₂=4/2, 8/4, 12/6 концентрические группы нечетные шестикатушечные имеют шаги катушек у_пi=13-2(i-1) с числом витков (1-x)w_к катушек с i=1, 6 и (1+х)w_к катушки с i=3, а четные пятикатушечные - у'_пi=12-2(i-1) с числом витков (1+x)w_к катушки с i=3 при w_к витках остальных катушек групп, где z=33 для 2p₁/2p₂=4/2, z=66 для 2p₁/2p₂=8/4, z=99 для 2p₁/2p₂=12/6, i=1...6 - номер катушки в группе, начиная с наружной, 2w_к - число витков каждого паза при значении х=0,52.