Способ активного контроля уровня несинусоидальности напряжения и тока

Способ активного контроля уровня несинусоидальности напряжения и тока

Иллюстрации

Показать все

Реферат

Изобретение относится к электротехнике и может быть использовано в действующих электроэнергетических системах, содержащих нелинейные электрические нагрузки, может быть использовано как составная часть автоматизированного активного контроля всех показателей качества электрической энергии.

Действующий межгосударственный стандарт ГОСТ 13109-97 "Нормы качества электрической энергии в системах электроснабжения общего назначения" предписывает уровень несинусоидальности напряжения оценивать коэффициентом искажения несинусоидальности напряжения и коэффициентом ν-той гармонической составляющей напряжения.

Для объективной и полной оценки качества электрической энергии есть смысл определять соответствующие показатели и относительно тока. Поэтому здесь идет речь и об уровне несинусоидальности тока.

Оценка уровня несинусоидальности напряжения и тока традиционно предполагает определение спектрального состава указанных характеристик электрической энергии. При этом обычно используется преобразование Фурье. Этот процесс неоднократно описывается в специальной литературе. Например, в [1].

Но преобразование Фурье в том виде, в котором оно применяется для контроля уровня несинусоидальности напряжения и тока в настоящее время, учитывает лишь целочисленные и лишь высшие гармонические составляющие указанных характеристик электрической энергии, хотя известно, что в спектральном составе напряжений и токов современных электроэнергетических систем присутствуют высшие дробные гармонические и субгармонические (частотой менее 50 Гц) составляющие.

Кроме того, существующие методы контроля уровней несинусоидальности напряжения и тока относятся к разряду пассивного контроля, то есть предполагают лишь получение информации о соответствующих показателях качества электроэнергии, не предпринимая попыток активного воздействия на последние.

Наиболее близким техническим решением к предлагаемому алгоритму активного контроля уровня несинусоидальности напряжения и тока является способ количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин [2].

Задачей изобретения является формирование структурной схемы алгоритма активного контроля уровня несинусоидальности напряжения и тока при учете не только соответствующих высших гармонических, но и субгармонических составляющих.

Технический результат достигается тем, что используется преобразование Фурье с предварительным определением фактического периода изменения напряжения и тока во времени, последующее оценивание уровня синусоидальности анализируемых величин и формирование, если это необходимо, сигнала управления для соответствующих корректирующих устройств.

В качестве корректирующих устройств здесь можно использовать любые технические решения, направленные на поддержание должного уровня несинусоидальности напряжения и тока. Например, фильтрокомпенсирующие устройства.

Классическое представление преобразования Фурье обычно представляют в виде:

где F(jω) - спектральная плотность оригинала функции f(t), ω - циклическая частота; ƒ(t) - описываемая временная функция.

Для данного случая нас больше должно интересовать обратное преобразование Фурье. Здесь целесообразнее его представить в виде тригонометрического ряда:

где A₀ - постоянная составляющая функции ƒ(t); , , , ..., и , , , ..., - синусные и косинусные коэффициенты на частоте 1-й, 2-й, и 3-й, ..., n-ой гармонических составляющих.

Поскольку здесь вместо функции ƒ(t) подразумеваются законы изменения во времени напряжения и тока, то упомянутый тригонометрический ряд следует представить в ином виде:

где U₀ и I₀ - постоянная составляющая функций u(t) и i(t); , , , ..., , , , , ..., и , , , ..., , , , , ..., - синусные и косинусные коэффициенты функций u(t) и i(t) на частоте 1-й, 2-й, и 3-й, ..., n-ой гармонических составляющих.

В математических интерпретациях этого ряда предполагается бесконечное по продолжительности суммирование его синусных и косинусных частей. Естественно в реальном случае это недостижимо. Поэтому в предложенных здесь формулировках суммирование ограничено частотой наивысшей из ощутимых в спектрах напряжения и тока гармоники n. Ее присутствие можно оперативно определить с помощью широко распространенных в настоящее время аналоговых или цифровых анализаторов (измерителей) спектра. Конечно, это определение будет весьма ориентировочным.

При определении численного значения n следует помнить, что чем больше будет его значение, тем достовернее будет ожидаемый результат.

Из математики известно, что

где T - период функции f(t), ν - номер текущей гармонической составляющей.

Применительно к данному случаю:

Исходные данные для выполнения анализа уровня несинусоидальности основных характеристик формируются в аналого-цифровом преобразователе в виде дискретных значений напряжений и токов. Определение постоянной составляющей временных функций, а также синусных и косинусных коэффициентов по представленным выше формулам на практике трудно осуществимо. Поэтому здесь следует использовать дискретное преобразование Фурье. Иначе эту операцию называют графоаналитическим разложением функции ƒ(t).

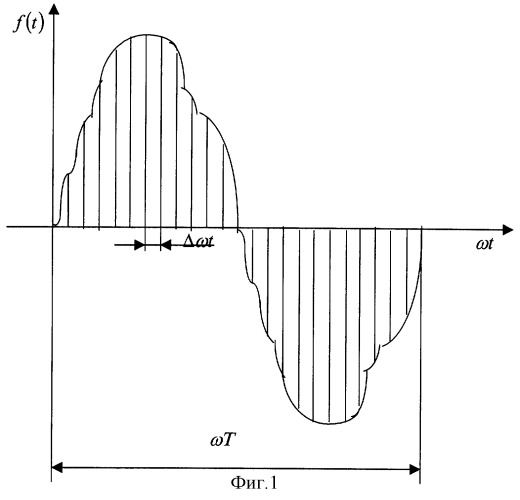
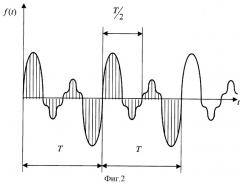
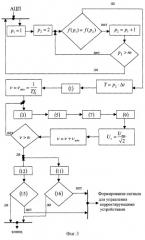
На чертежах представлено следующее: на фиг.1 - иллюстрация графоаналитического разложения функции ƒ(t), на фиг.2 - иллюстрация процесса определения фактического периода изменения анализируемых характеристик электрической энергии, на фиг.3 - структурная схема алгоритма активного контроля уровня несинусоидальности напряжения, на фиг.4 - структурная схема алгоритма активного контроля уровня несинусоидальности тока.

На фиг.1 проиллюстрирован процесс преобразования аналоговых сигналов в дискретные в аналого-цифровом преобразователе.

Здесь аналоговая функция разбивается по оси абсцисс на равные участки Δωt. Иначе эти участки называют квантованиями. При определении числа этих квантований для выполнения поставленной здесь задачи имеет смысл воспользоваться рекомендациями теоремы Котельникова. Из следствий этой теоремы оказывается, что число квантований на период функции должно определяться по формуле N=2^k, где k - любое натуральное число (k=1, 2, 3, 4, 5, ...). Именно из этого условия, кроме быстродействия и многоканальности, следует подбирать аналого-цифровой преобразователь.

Суммирование функции ƒ(t), судя по фиг.1, должно производиться по аргументу ωt. Поэтому постоянная составляющая, а также синусные и косинусные коэффициенты для этой функции в этом случае предстанут в несколько ином виде:

Применительно к напряжению и току эти формулы перепишутся так:

Учитывая, что

последние формулировки с учетом дискретности функций u(t) и i(t) можно преобразовать и представить в ином виде.

Так, постоянные составляющие анализируемых функций с учетом этого равенства преобразуется следующим образом:

где u_p(t) и i_p(t) - дискретные p-тые значения функций u(t) и i(t); p - текущий номер квантования.

Синусные коэффициенты на частоте ν-той гармонической составляющей определятся так:

где (ωt)_p - количественное значение аргумента функций u_p(t) и i_р(t) в радианах, определяемое по формуле

Аналогично для косинусных коэффициентов на частоте ν-той гармонической составляющей:

Далее, основываясь на свойствах математических формулировок, можно определить амплитуды ν-тых гармонических составляющих напряжения и тока как геометрическую сумму соответствующих синусного и косинусного коэффициентов:

Начальные фазы напряжения и тока на частоте этой гармонической составляющей фаза (угол сдвига нулевого значения гармонической составляющей относительно начала отсчета) определятся по формулам

В результате выполненных преобразований получается, что

Теперь появилась возможность определить действующие значения напряжений и токов на частоте каждой гармонической составляющей:

Приведенная выше методика определения спектрального состава напряжения и тока имеет достаточно серьезное ограничение, которое можно отнести к разряду недостатков преобразования Фурье, ограничивающее его использование для решения технических задач: она позволяет выявлять лишь целочисленные гармонические составляющие. Это особенно ощутимо для современных электроэнергетических систем, насыщенных силовыми электронными аппаратами и прочими нелинейными элементами, обеспечивающих электрической энергией технологические процессы, характеризующиеся нелинейными вольт-амперными и вебер-амперными характеристиками, снабженных протяженными линиями электропередач большой мощности. В современных электроэнергетических системах отмечается значительная доля присутствия дробных высших гармонических составляющих, учет которых при использовании изложенной выше методики невозможен.

Чрезвычайно ощутим недостаток этой методики, заключающийся в игнорировании субгармонических составляющих, частоты которых менее частоты основной гармоники (в России 50 Гц). А ведь именно субгармонические составляющие оказывают крайне отрицательное влияние на биологические объекты, в том числе и на человеческий организм.

Решение поставленной задачи исходя из анализа [2] относительно простое: достаточно просто-напросто наиболее достоверно определить период изменения изменяющейся во времени величины. Но порой это сделать очень непросто. И выполняется эта операция исходя из предположения, что напряжение и ток есть периодически изменяющиеся величины, что в связи с катастрофическим ухудшением качества электрической энергии становится все более сомнительным. В таком случае придется задаться периодом наименьшей гармонической составляющей и лишь после этого использовать вышеуказанные математические формулировки для выяснения спектрального состава напряжения и тока.

В реальном случае все-таки чаще всего напряжение и ток - периодически изменяющиеся величины. В этом случае существует вполне реальная возможность определить фактический период изменения этих величин. Эта процедура проиллюстрирована на фиг.2.

В этом случае надо рассматривать несколько визуально определенных периодов периодически изменяющейся функции. Эти несколько периодов необходимо проводить через аналого-цифровой преобразователь, преобразуя их во множество дискретных величин. Процедура определения фактического периода периодически изменяющейся функции заключается в отыскании групп с одинаковыми дискретными значениями анализируемой функции. Одинаковые дискретные значения здесь могут определяться лишь с той иной, установленной заранее, степенью достоверностью, поскольку абсолютное выполнение требования N=2^k невозможно без предварительного определения периода. После этого, если позволяет разрешительная способность аналого-цифрового преобразователя, есть смысл в соответствии с этим равенством уточнить число квантований за промежуток времени, равный ориентировочно определенному периоду, и уточнить в оговоренном здесь порядке количественное значение последнего. Если же и в этом случае опять не достигнуто абсолютного равенства групп дискретных величин, то количество квантований, приходящихся на период, следует вновь уточнить... И так далее до тех пор, пока либо не будет достигнуто абсолютное равенство групп дискретных величин, тогда фактический период будет определяться временным интервалом одной из упомянутых групп дискретных величин, либо разница между соответствующими величинами рассматриваемых групп не начнет явно увеличиваться.

В последнем случае увеличение разницы между соответствующими величинами групп дискретных величин свидетельствует либо о неверном определении этих групп и тогда после предварительного уменьшения допустимой ошибки при определении равенства соответствующих дискретных величин, увеличивая рассматриваемый временной промежуток, следует повторить определение оговоренных ранее групп с последующим более достоверным определением фактического периода периодически изменяющейся функции либо о недостаточной разрешающей способности аналого-цифрового преобразователя. В этом случае, если нет возможности использовать аналого-цифровой преобразователь с более высокой разрешающей способностью, за действительное значение искомой величины следует принять период, определенный при наименьшем различии соответствующих величин рассматриваемых групп. Естественно, степень достоверности определения фактического периода периодически изменяющейся функции будет тем больше, чем больше разрешающая способность аналого-цифрового преобразователя, чем меньше временной диапазон одного квантования, чем больше число квантований приходится на один период.

Подставив таким образом определенный фактический период изменения интересующей исследователя функции (напряжения или тока) в приведенные выше математические формулировки, можно определить спектральный состав напряжения и тока.

Частота минимальной гармонической составляющей определяется как обратная величина фактического периода исследуемой функции:

Частоты прочих гармонических составляющих определяются по формуле

где v - текущий номер гармоники, имеющий только положительные целочисленные значения (ν=1, 2, 3, 4, ...).

Частота минимальной гармонической составляющей вполне может оказаться гораздо меньше принятой в той или иной стране частоты основной гармонической составляющей (в России 50 Гц):

В этом случае речь идет о субгармонических составляющих.

Фактическую частоту основной гармонической составляющей целесообразно определять по максимальной величине ее амплитуды.

Если номер основной гармонической составляющей принять равным единице, а номера прочих гармоник обозначить символом ν, то при соблюдении последнего неравенства обнаружатся номера упомянутых гармонических составляющих, меньшие единицы (субгармонические составляющие), а также дробные номера:

Теперь, наконец, появилась возможность определить степень соответствия действительных спектров напряжения и тока своим нормативным требованиям. Эти требования могут быть, в случае необходимости, дифференцированы для каждого узла электроэнергетической системы. В иных случаях целесообразно будет ограничиться требованиями действующего межгосударственного стандарта "Нормы качества электрической энергии в системах электроснабжения общего назначения" ГОСТ 13109-97.

Упомянутым здесь стандартом определено два показателя качества электрической энергии, оценивающих уровень несинусоидальности напряжения: коэффициент искажения несинусоидальности кривой напряжения k_U и коэффициент ν-той гармонической составляющей напряжения k_νU. Согласно рекомендациям этого же стандарта эти показатели определяются так:

где U_ν - действующее значение напряжения на частоте ν-той гармонической составляющей; U₁ - действующее значение напряжения на частоте основной гармонической составляющей; n - наибольшее число зарегистрированных гармонических составляющих (в тексте цитируемого межгосударственного стандарта наибольшее число гармонических составляющих ограничено цифрой 40).

К сожалению, эти равенства не учитывают факт присутствия в спектре анализируемого напряжения дробных высших гармонических и субгармонических составляющих. В таком случае для оценки уровня несинусоидальности напряжения коэффициент искажения несинусоидальности кривой напряжения предлагается определять несколько иначе:

где ν_min - номер гармонической составляющей, характеризующейся наименьшей частотой

Для действенного активного контроля качества электрической энергии при помощи АСАК ПКЭ необходимо оценивать уровень несинусоидальности не только напряжения, но и тока. В таком случае соответствующие показатели качества электрической энергии предстанут следующим образом:

- коэффициент искажения несинусоидальности кривой тока

- коэффициент ν-той гармонической составляющей тока

где I_ν - действующее значение тока на частоте ν-той гармонической составляющей; I₁ - действующее значение тока на частоте основной гармонической составляющей.

Действующим стандартом оговорены и нормативные значения коэффициента искажения синусоидальности и коэффициента отдельных гармонических составляющих напряжения. Эти нормативы нашли достаточно широкое применение в системах электроснабжения общего назначения. Нормативные значения для коэффициента искажения синусоидальности и коэффициента отдельных гармонических составляющих токов вполне можно оценивать в том же процентном соотношении, в каком рекомендовано стандартом оценивать подобные коэффициенты для напряжения. Однако в ряде частных случаев нормативные значения для указанных коэффициентов приходится несколько ужесточать.

Один из завершающих этапов анализа уровней несинусоидальности напряжения и тока заключается в проверке соответствия упомянутых коэффициентов своим нормативным величинам. Эта операция предполагает проверку неравенств:

где ε_U, ε_νU, ε_I, ε_νI, - нормативные значения коэффициентов соответственно искажения синусоидальности кривой и ν-той гармонической составляющей напряжения и тока.

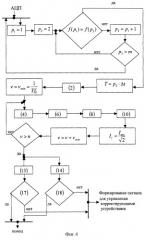
На фиг.3 представлена рекомендуемая структурная схема алгоритма анализа уровня несинусоидальности напряжения в узле электроэнергетической системы. Здесь р₁ и р₂ - текущие величины (номера) квантования анализируемой кривой (фиг.2); Δt - время дискретизации; m - количество квантований, зависящее обычно от разрешающей способности аналого-цифрового преобразователя.

Здесь в первых пяти блоках по изложенной выше методике определяется фактический период изменения во времени анализируемого напряжения. Далее определяются по формуле (1) постоянная составляющая этого напряжения и номер минимальной гармонической составляющей. Затем для каждой гармонической составляющей оцениваемого спектра напряжения по формулам (3), (5), (7) и (9) определяются синусные и косинусные коэффициенты, ее амплитудное значение и начальная фаза (угол сдвига нулевого значения гармонической составляющей относительно начала отсчета), по формулам (12) и (11) определяются коэффициент искажения несинусоидальности кривой и коэффициент ν-той гармонической составляющей напряжения. А в двух последних блоках по неравенствам (15) и (16) выполняется проверка соответствия найденных показателей качества электрической энергии своим нормативным значениям. При нарушении этого соответствия есть смысл приступить к формированию сигнала управления для соответствующих корректирующих устройств.

Параллельно с анализом уровня несинусоидальности кривой напряжения вполне возможно осуществление анализа уровня несинусоидальности кривой тока. Структурная схема такого анализа приведена на фиг.4.

Здесь, так же как и при анализе уровня несинусоидальности напряжения, в первых пяти блоках определяется фактический период изменения во времени анализируемого тока. Потом по формуле (2) определяется постоянная составляющая тока и номер его минимальной гармонической составляющей. Далее для каждой гармонической составляющей оцениваемого спектра тока по формулам (4), (6), (8) и (10) определяются синусные и косинусные коэффициенты, ее амплитудное значение и начальная фаза (угол сдвига нулевого значения гармонической составляющей относительно начала отсчета), по формулам (13) и (14) определяются коэффициент искажения несинусоидальности кривой и коэффициент ν-той гармонической составляющей тока. Затем в двух последних блоках по неравенствам (17) и (18) выполняется проверка соответствия найденных показателей качества электрической энергии своим нормативным значениям. При нарушении этого соответствия здесь, так же как и в предыдущем случае, есть смысл приступить к формированию сигнала управления для соответствующих корректирующих устройств.

Так выглядят структурные схемы алгоритма активного контроля уровня несинусоидальности напряжения и тока в современных электроэнергетических системах.

Источники информации

1. Буняк А.Ф. Использование дискретного преобразования Фурье для определения параметров качества электроэнергии вычислительными устройствами. Известия вузов. Энергетика (Минск), 1982, №6. - С.7-12.

2. Способ количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин. Г.А.Большанин, И.Н.Охлопков, С.В.Видерников, Е.А.Безносов, А.В.Манахов, С.А.Зимарев, М.А.Алферов. - Патент РФ 2122186, МКИ 6 G 01 J 3/18. - Братский индустриальный институт, №96112228/25; Заявл. 14.06.96; Опубл. 20.11.98. Бюл. №32.

Способ активного контроля уровня несинусоидальности напряжения и тока, предусматривающий графоаналитическое разложение спектрального состава периодически изменяющихся напряжения и тока, при котором осуществляют определение фактического периода изменения этих величин, номер гармонической составляющей, характеризующейся наименьшей частотой, и действующие значения каждой гармонической составляющей, отличающийся тем, что определяют коэффициент k_U искажения синусоидальности кривой напряжения по формуле

где ν_min - номер гармонической составляющей, характеризующейся наименьшей частотой;

U_ν - действующее значение напряжения на частоте v-той гармонической составляющей;

U₁ - действующее значение напряжения на частоте основной гармонической составляющей;

n - наибольшее число зарегистрированных гармонических составляющих,

определяют коэффициент искажения синусоидальности тока по формуле

где I_ν - действующее значение тока на частоте ν-той гармонической составляющей;

I₁ - действующее значение тока на частоте основной гармонической составляющей,

определяют коэффициент ν-той гармонической составляющей тока по формуле

проверяют соответствие этих показателей их нормативным значениям и при нарушении этого соответствия формируют сигнал управления устройствами, корректирующими уровень несинусоидальности напряжения и тока.