Цифровой обнаружитель сложных сигналов
Иллюстрации
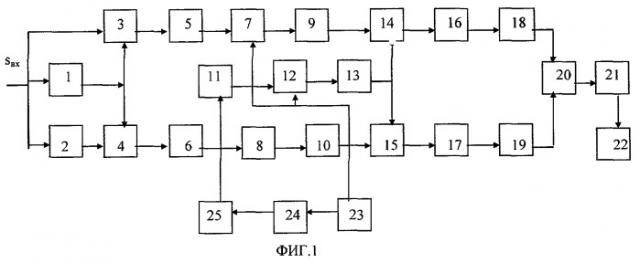
Показать всеЦифровой обнаружитель сложных сигналов относится к области радиосвязи, системам передачи дискретной информации, использующим сложные широкополосные сигналы на основе рекуррентных псевдослучайных последовательностей максимального периода и сигналов Голда с фазовой двоичной манипуляцией. Достигаемый технический результат - возможность обнаружения сложных радиосигналов с неизвестной несущей частотой, заданной областью допустимых значений и случайной начальной фазой возможности цифровой обработки принимаемого сигнала при априорной неопределенности его несущей частоты. В цифровом обнаружителе используются алгоритмы дискретного преобразования Фурье и "скоростной" свертки принимаемого и опорного сигналов, что позволяет производить беспоисковое обнаружение сложных сигналов с большими базами. В обнаружителе цифровой согласованный фильтр осуществляет обработку на видеочастоте с использованием стандартных цифровых узлов и элементов. Цифровой обнаружитель сложных сигналов содержит перемножители (3,4,14,15), фазовращатель на π/2 (2), схему задержки на длительность элемента сигнала (1), фильтры нижних частот (5,6), аналого-цифровые преобразователи (7,8,12), микропроцессорные системы дискретного (9,10) преобразования Фурье, микропроцессорные системы обратного дискретного преобразования Фурье (16,17), генератор опорной псевдослучайной последовательности (11), микропроцессорная система дискретного преобразования Фурье опорной псевдослучайной последовательности (13), квадраторы (18,19), сумматор (20), арифметическое устройство извлечения квадратного корня из числа (21), пороговое устройство (22), генератор импульсов дискретизации (23), делитель частоты на два (24), генератор тактовых импульсов (25), соединенные соответствующими функциональными связями. 2 ил.
Реферат
Изобретение относится к области радиосвязи, системам передачи дискретной информации, использующих сложные широкополосные сигналы на основе псевдослучайных последовательностей максимального периода и сигналов Голда с двоичной фазовой манипуляцией (0, π) и предназначено для построения цифровых обнаружителей сложных сигналов.
Наиболее близким по техническим признакам к настоящему устройству является оптимальный обнаружитель сложных сигналов с неизвестной амплитудой и случайной начальной фазой [1, с.350]. Это устройство обладает максимальной помехоустойчивостью в нормальных шумах при известных параметрах принимаемого сигнала, кроме амплитуды и начальной фазы высокочастотного колебания. Обнаружитель прототипа содержит два перемножителя, генератор гармонических колебаний несущей частоты, фазовращатель на π/2, два идентичных согласованных фильтра, два квадратора и сумматор. Генератор гармонических опорных колебаний с фазовращающей цепью создает два квадратурных гармонических колебания Cos(ω0t) и Sin(ω0t), где ω0 - несущая частота принимаемого сигнала. Применение квадратурных каналов позволяет устранить влияние случайной начальной фазы несущего колебания. На выходах перемножителей входной радиосигнал переводится в видеочастотную область и выделяются элементы сложного сигнала, которые обрабатываются двумя идентичными согласованными фильтрами.
Недостатком прототипа является то, что для нормальной работы обнаружителя требуется априорная информация о частоте принимаемого сигнала для перевода радиосигнала в видеообласть и сложность изготовления согласованных фильтров, особенно при больших базах используемых сигналов.
Для устранения отмеченных недостатков аналогового обнаружителя прототипа предлагается использовать цифровой обнаружитель сложных сигналов. Ввиду того, что несущая частота принимаемого сигнала в силу разных причин не известна, с требуемой точностью предлагается для выделения модулирующей функции из смеси радиосигнала и помехи использовать автокорреляционный метод обработки сигнала, как оптимальный метод приема сигналов неизвестной формы. Автокорреляционный метод применительно к задаче выделения элементов сложного сигнала состоит в перемножении принимаемого радиосигнала и задержанного на длительность элемента сложного сигнала.
Фазоманипулированный псевдослучайной последовательностью принимаемый радиосигнал может быть представлен в виде
s1(t)=Adi[rect(t-iτ)]Cos(ω0t+ϕ0), 0≤t≤Tc, i=0,1 ... N-1
где А - амплитуда сигнала;
ω0, ϕ0 - несущая частота и начальная фаза гармонического колебания;
Тc - длительность сигнала;
τ - длительность элемента сигнала;
di=(1, -1) - элементы псевдослучайной последовательности;
На интервале длительности элемента сигнала результат перемножения будет
y1(t)=s1(t)s1(t-τ)=AdiCos(ω0t+ϕ0)Adi-1Cos(ω0(t-τ)+ϕ0)=
=1/2A2didi-1[Cos(ω0τ)+Cos(2ω0t-ω0τ+2ϕ0)].
После отфильтрования высокочастотной составляющей с помощью фильтра нижних частот получим
Z1(t)=1/2A2didi-1Cos(ω0τ).
Как видно, что при автокорреляционной обработке устраняется зависимость от начальной фазы ϕ0 гармонического колебания, но появляется коэффициент Cos(ω0τ), зависящий от значения несущей частоты и длительности элемента сигнала. Для устранения этой зависимости необходимо ввести квадратурный канал. Принимаемый. радиосигнал пропускается через фозовращательную цепь на π/2 и получаем
S2(t)=Adi[rect(t-iτ)]Cos(ω0t+ϕ0-π/2)=
=Adi[rect(t-iτ)]Sin(ω0t+ϕ0), 0≤t≤Tc, i=0,1 ... N-1.
После перемножения в квадратурном канале получим
y2(t)=s2(t)s1(t-τ)=AdiSin(ω0t+ϕ0)Adi-1Cos(ω0(t-τ)+ϕ0)=
=1/2A2didi-1[Sin(ω0τ)+Sin(2ω0t-ω0τ+2ϕ0)].
На выходе фильтра нижних частот второго канала получим
z2(t)=1/2A2didi-1Sin(ω0τ).
Заметим, что произведение элементов последовательности didi-1 из элементов (1, -1) эквивалентно сложению по модулю два элементов didi-1, составленных из (1, 0). Одно из свойств линейных рекуррентных последовательностей состоит в том, что, если последовательность сложить по модулю два с этой же последовательностью, но сдвинутой на некоторое неравное периоду сигнала число элементов [2, с.58], то получается та же последовательность, но с другим сдвигом. Это же справедливо и для последовательностей Голда, поскольку они получаются суммированием по модулю два двух различных рекуррентных последовательностей максимального периода. Таким образом, последовательность
dk=didi-1, k=0, 1 ... N-1
будет той же последовательностью, что и принимаемая, но с другим запаздыванием.
Следовательно, на выходах фильтров нижних частот в двух каналах выделяется модулирующая функция dk с некоторыми неизвестными постоянными коэффициентами Cos(ω0τ) и Sin(ω0τ). Далее в обоих каналах осуществляется идентичная цифровая обработка выделенной модулирующей функции принимаемого сигнала.
Аналоговые сигналы с выходов фильтров нижних частот в обоих каналах подвергаются дискретизации. Частота дискретизации связана с максимальной частотой спектра модулирующей функции. Обычно излучаемый сигнал на передающей стороне ограничивается по спектру главным лепестком спектра модулирующей функции. Ширина главного лепестка определяется длительностью элементарного символа и равна тактовой частоте fτ=1/τ, которую и следует принять за максимальную частоту спектра дискретизируемого сигнала, то есть fmax=fτ. Тогда, согласно теореме Котельникова, частота дискретизации выбирается равной
fd≥2fmax=2fτ.
Для выделения сигнала воспользуемся дискретной сверткой двух функций времени - сигнала с выхода квадратурного канала и опорного сигнала, вырабатываемого в генераторе копии сигнала обнаружителя. Вычисление дискретной свертки целесообразно производить по алгоритму не во временной, а в спектральной области, который требует меньшего числа операций, особенно при использовании "быстрого преобразования Фурье".
Поскольку цифровой обнаружитель должен выдавать на выходе сигнал, совпадающий по форме со взаимно-корреляционной функцией принимаемого и опорного сигналов, то обработка сигнала может быть осуществлена по алгоритму "скоростной" свертки. После аналого-цифрового преобразования последовательность закодированных в цифру отсчетов
x1(k)=z1(kTd), k=0, 1 ... Nd-1,
где Td - интервал дискретизации, равный Td=1/fd;
Nd=Ец[Тc/Td] - число выборок на длительности сигнала;
Ец[х] - целая часть числа х,
подается на микропоцессорную систему, осуществляющую дискретное преобразование Фурье (ДПФ). С ее выхода последовательность спектральных коэффициентов
S1(n)=ДПФ[х1(k)], n=0, 1 ... Nd-1
перемножается с последовательностью спектральных коэффициентов
S0(n)=ДПФ[x0(k)], n=0, 1 ... Nd-1,
полученных от опорной последовательности генератора копии сигнала. Полученная таким образом последовательность
S10(n)=S1(n)S0(n), n=0, 1... Nd-1
подвергается в микропрцессорной системе обратному дискретному преобразованию Фурье (ОДПФ)
Н1(k)=ОДПФ[S10(n)], k=0,1 ... Nd-1.
На выходе второго квадратурного канала аналогично получим
S2(n)=ДПФ[x2(k)], S20(n)=S2(n)S0(n) и Н2(k)=ОДПФ[S20(n)].
В современной практике ДПФ и ОДПФ осуществляется в одном и том же устройстве. Для устранения влияния коэффициентов Cos(ω0τ) Sin(ω0τ) выходы обоих каналов возводятся в квадрат и суммируются. Окончательно выходной сигнал цифрового обнаружителя имеет вид
H(k)=[H12(k)+H22(k)]l/2.
Заявленное устройство с цифровой обработкой сложного фазоманипулированного (0, π) сигнала приведено на фиг.1. Оно содержит:
1 - схема задержки на длительность элемента сигнала τ;
2 - фазовращатель на π/2;
3, 4 - первый и второй перемножители;
5, 6 - первый и второй фильтры нижних частот;
7, 8 - первый и второй аналого-цифровые преобразователи;
9, 10 - первая и вторая микропроцессорнные системы ДПФ;
11 - генератор опорной псевдослучайной последовательности;
12 - третий аналого-цифровой преобразователь;
13 - микропроцессорная система ДПФ опорной последовательности;
14, 15 - третий и четвертый перемножители;
16, 17 - первая и вторая микропоцессорные системы ОДПФ;
18, 19 - первый и второй квадраторы;
20 - сумматор;
21 - арифметическое устройство излечения квадратного корня из числа;
22 - пороговое устройство;
23 - генератор импульсов дискретизации;
24 - делитель частоты на два;
25 - генератор тактовых импульсов;
Устройство работает следующим образом. Принимаемый радиосигнал со входа обнаружителя поступает на первый вход первого перемножителя (3) непосредственно, а на первый вход второго перемножителя (4) - через фазовращатель на π/2 (2). На вторые входы перемножителей (3) и (4) радиосигнал поступает через элемент задержки (1) на длительность элемента сигнала τ. Эпюры сигналов на выходах различных устройств цифрового обнаружителя приведены на фиг.2. На первом графике приведена псевдослучайная последовательность (модулирующая функция) u(t), которую необходимо выделить для обработки, и опорная псевдослучайая последовательность uo(t), которую вырабатывает генератор копии сигнала. Опорная последовательность есть зеркальное отражение принимаемой последовательности, т.е. uo(t)=u(Tc-t), где Тс - длительность сигнала. Здесь приведены рекуррентные последовательности максимального периода из 15 элементов. На втором графике приведена функция s1(t) - гармонический сигнал, промодулированный по фазе последовательностью u(t) с некоторой задержкой. На чертежах, где приведены по две зависимости, одна из них поднимается (или опускается) для наглядности. На третьем графике приведены зависимости y1(t) и y2(t) на выходах первого и второго перемножителей. На четвертом графике изображены сигналы (х1k и х2k) с выходов фильтров низших частот после дискретизации их в аналого-цифровых преобразователях. Сигналы х1k и х2k представляют собой последовательности цифровых отсчетов, следующих через интервалы дискретизации Тd. На последнем графике приведены обратные дискретные преобразования Фурье для дискретных сверток сигнала первого квадратурного канала и опорной последовательности Н1k дискретной свертки сигнала второго канала и опорной последовательности H2k и результирующей функции Hk=(H1k 2+H2k 2)1/2
являющейся функцией взаимной корреляции принимаемого сигнала и опорной последовательности генератора копии сигнала. Сигнал Нk и является выходом цифрового обнаружителя, по которому осуществляется обнаружение сигнала. После выбора максимального отсчета Hk max и сравнения его с порогом принимается решение об обнаружении сигнала, в случае его превышения.
Таким образом, совокупность введенных устройств и их связей позволяет устранить влияние априорной неопределенности о несущей частоте и осуществить цифровую обработку принимаемого сигнала для его обнаружения, что отсутствовало в прототипе.
Следовательно, техническое решение соответствует критерию "новизны". Кроме того, так как требуемый технический результат достигается всей вновь введенной совокупностью существенных признаков, которая в известной патентной и научно-технической литературе не обнаружена на день подачи заявки, изобретение соответствует критерию "изобретательский" уровень.
Источники информации
1. Варакин Л.Е. Системы связи с шумоподобными сигналами. - М.: Радио и связь, 1985. - 384 с., ил.
2. Дядюнов Н.Г. и Сенин А.И. Ортогональные и квазиортогональные сигналы. Под ред. Е.М.Тарасенко. М.: Связь, 1977. - 224 с., ил.
Цифровой обнаружитель сложных сигналов, содержащий первый и второй перемножители, фазовращатель на π/2, отличающийся тем, что дополнительно введены схема задержки на длительность элемента сигнала, первый и второй фильтры нижних частот, первый и второй аналого-цифровой преобразователи, первая и вторая микропроцессорные системы дискретного преобразования Фурье, генератор опорной псевдослучайной последовательности, третий аналого-цифровой преобразователь, микропроцессорная система дискретного преобразования Фурье опорной псевдослучайной последовательности, третий и четвертый перемножители, первая и вторая микропроцессорные системы обратного дискретного преобразования Фурье, первый и второй квадраторы, сумматор, арифметическое устройство извлечения квадратного корня из числа, пороговое устройство, генератор импульсов дискретизации, делитель частоты на два, генератор тактовых импульсов, причем первый вход первого перемножителя подключен ко входу обнаружителя непосредственно, первый вход второго перемножителя подключен ко входу обнаружителя через фазовращатель на π/2, вторые входы первого и второго перемножителей подключены ко входу обнаружителя через схему задержки на длительность элемента сигнала, выход первого перемножителя через последовательно соединенные первый фильтр нижних частот, первый аналого-цифровой преобразователь, первую микропроцессорную систему дискретного преобразования Фурье, третий перемножитель, первую микропроцессорную систему обратного дискретного преобразования Фурье и первый квадратор подключен к первому входу сумматора, выход второго перемножителя через последовательно соединенные второй фильтр нижних частот, второй аналого-цифровой преобразователь, вторую микропроцессорную систему дискретного преобразования Фурье, четвертый перемножитель, вторую микропроцессорную систему обратного дискретного преобразования Фурье и второй квадратор подключен ко второму входу сумматора, один выход генератора импульсов дискретизации через последовательно соединенные делитель частоты на два, генератор тактовых импульсов, генератор опорной псевдослучайной последовательности, третий аналого-цифровой преобразователь и микропроцессорную систему дискретного преобразования Фурье опорной псевдослучайной последовательности подключен ко вторым входам третьего и четвертого перемножителей, другой выход генератора импульсов дискретизации подключен ко вторым входам первого, второго и третьего аналого-цифровых преобразователей, выход сумматора через арифметическое устройство извлечения квадратного корня из числа подключен ко входу порогового устройства, выход порогового устройства является выходом цифрового обнаружителя сложных сигналов.