Адаптивная система управления для динамических объектов с периодическими коэффициентами

Адаптивная система управления для динамических объектов с периодическими коэффициентами

Иллюстрации

Показать все

Реферат

Изобретение относится к технической кибернетике и может быть использовано в системах регулирования объектами, параметры которых - периодически меняющиеся величины.

Наиболее близким техническим решением к предлагаемому является адаптивная система стабилизации /Авторское свидетельство СССР №1019400, кл. G 05 В 13/02, 1983 (прототип)/, содержащая объект регулирования, блок задания коэффициентов, сумматор, первый умножитель, интегратор, второй умножитель. Сигналы с выходов объекта регулирования поступают на соответствующие входы блока задания коэффициентов, который представляет собой блок умножителей. В блоке задания коэффициентов происходит умножение сигнала с каждого выхода объекта регулирования на постоянный коэффициент. Сигналы с выходов блока задания коэффициентов поступают на соответствующие входы блока суммирования, где складываются. Сигнал с выхода блока суммирования приходит на первый вход второго умножителя и на оба входа первого умножителя. В первом умножителе происходит умножение сигнала с выхода блока суммирования на этот же сигнал. Сигнал с выхода первого умножителя поступает на вход интегратора. Сигнал с выхода интегратора поступает на второй вход второго умножителя. Во втором умножителе происходит умножение сигнала с выхода блока суммирования на сигнал с выхода интегратора. Сигнал с выхода второго умножителя поступает на вход объекта регулирования.

Недостатком этой системы в случае наличия в объекте периодически изменяющихся параметров является неустойчивость положения равновесия.

Задачей изобретения является обеспечение асимптотической устойчивости положения равновесия системы при наличии в объекте периодически изменяющихся параметров.

Решение поставленной задачи достигается тем, что в систему, содержащую блок задания коэффициентов, первый сумматор, последовательно соединенные первый умножитель, интегратор, второй умножитель и объект регулирования, выходы которого соединены с соответствующими входами блока задания коэффициентов, входы первого сумматора подключены к соответствующим выходам блока задания коэффициентов, вместо интегратора введены второй сумматор и блок задержки, при этом первый вход второго сумматора подключен к выходу первого умножителя, второй вход - к выходу блока задержки, выход второго сумматора связан с входом второго умножителя и с входом блока задержки.

Технический результат заключается в возможности стабилизации адаптивной системы при наличии объектов с параметрами, элементы которых являются периодическими функциями.

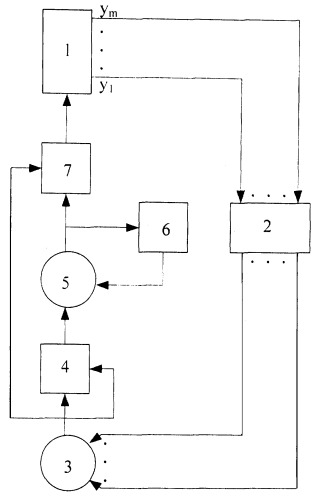
На чертеже представлена блок-схема системы. Система содержит объект регулирования 1, блок задания коэффициентов 2, первый сумматор 3, первый умножитель 4, второй сумматор 5, блок задержки 6, второй умножитель 7.

Объект регулирования описывается уравнением

где x∈Rⁿ - вектор состояний объекта регулирования, А(t+T), b(t+T) - нестационарные соответственно матрица и вектор с периодическими коэффициентами, Т - период изменения коэффициентов, L - матрица выхода, символ * означает транспонирование, y=(y₁,...y_m) - выход объекта регулирования, u- скалярное управляющее воздействие, удовлетворяющее уравнению

где χ - настраиваемый коэффициент, α₀ - m-мерный вектор коэффициентов блока 2 задания коэффициентов, выбираемый из условия

- гурвицевый квазиполином степени n-1 с положительным старшим коэффициентом (α(λ) - числитель передаточной функции объекта регулирования);

y - m-мерный вектор выходных координат объекта. Используя критерий гиперустойчивости Попова, можно показать, что реализуемый алгоритм настройки

где β>0 - число, обеспечивает асимптотическую устойчивость системы.

Система функционирует следующим образом.

Сигналы с выходов объекта регулирования 1 поступают на соответствующие входы блока задания коэффициентов 2. В блоке задания коэффициентов 2 происходит умножение сигнала с каждого выхода объекта регулирования 1 на постоянный коэффициент. Сигналы с выходов блока задания коэффициентов 2 поступают на соответствующие входы первого блока суммирования 3. Сигнал с выхода блока суммирования 3 приходит на второй вход второго умножителя 7 и на оба входа первого умножителя 4, сигнал с выхода первого умножителя 4 идет на первый вход второго сумматора 5. Сигнал с выхода второго сумматора 5 идет на первый вход второго умножителя 7 и на вход блока задержки 6, сигнал с выхода блока задержки 6 идет на второй вход второго сумматора 5. Сигнал с выхода второго умножителя 7 идет на вход объекта регулирования 1.

Данное устройство может быть реализовано промышленным способом, на основе стандартной элементной базы.

Адаптивная система управления для динамических объектов с периодическими коэффициентами, содержащая блок задания коэффициентов, первый сумматор, первый умножитель, последовательно соединенные второй умножитель и объект регулирования, выходы которого соединены с соответствующими входами блока задания коэффициентов, входы первого сумматора подключены к соответствующим выходам блока задания коэффициентов, отличающаяся тем, что в нее введены второй сумматор и блок задержки, при этом первый вход второго сумматора подключен к выходу первого умножителя, второй вход - к выходу блока задержки, выход второго сумматора связан с первым входом второго умножителя и с входом блока задержки, выход первого сумматора соединен с первым и вторым входами первого умножителя и со вторым входом второго умножителя.