Устройство для обнаружения и исправления ошибок в полиномиальной системе класса вычетов
Патент 2267808
Авторы
- Емельяненко Сергей Васильевич (RU)
- Калмыков Игорь Анатольевич (RU)
- Лисицын Александр Владимирович (RU)
Правообладатели
Классы МПК
Устройство для обнаружения и исправления ошибок в полиномиальной системе класса вычетов
Иллюстрации
Устройство относится к области автоматики и вычислительной техники и может быть использовано как для контроля и исправления ошибки при передаче информации, так и при проведении арифметических операций в ЭВМ. Техническим результатом является уменьшение объема оборудования, повышение скорости обнаружения и исправления ошибок. Указанный результат достигается за счет того, что устройство содержит два блока вычисления синдрома ошибки по контрольным основаниям, выполненных на двухслойной нейронной сети, регистр, блок памяти, выходной сумматор, а также за счет применения полиномиальной системы вычетов, в которой в качестве основания системы используется минимальные многочлены, определенные в расширенных полях Галуа GF (2ν) и нейросетевых технологий. 3 ил., 2 табл.
Реферат
Устройство относится к области автоматики и вычислительной техники и может быть использовано как для контроля и исправления ошибки при передаче информации, так и при проведении арифметических операций в ЭВМ.
Известно устройство для обнаружения и исправления ошибок в системе остаточных классов (а.с. №714399, кл. G 06 F 11/08, 1980 г.), содержащее регистр, вход которого соединен со входом устройства, два блока модульной свертки, три сумматора, причем выход третьего сумматора является выходом устройства, блок памяти.
Недостатком известного устройства является его сложность и низкое быстродействие, вследствие наличия большого объема оборудования.
Основной задачей является уменьшение оборудования и повышение скорости исправления ошибок.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является повышение скорости обнаружения и коррекции ошибок и снижение объема оборудования.
Указанный техническим результат достигается за счет того, что заявленное устройство содержит два блока вычисления синдрома ошибки по контрольным основаниям, причем эти блоки выполнены на двухслойной нейронной сети, причем первый выход регистра соединен с первыми выходами блоков вычисления синдрома ошибки, второй и третий выход регистра подключены соответственно по вторым выходам первого и второго блоков вычисления синдрома ошибки, выходы которых подключены к входам блока памяти; а также за счет применения полиномиальной системы вычетов (ПСКВ), в которой в качестве основания системы используется минимальные многочлены pi(z), i=1,2,...,n, определенные в расширенных полях Галуа GF(2ν) и нейросетевых технологий.
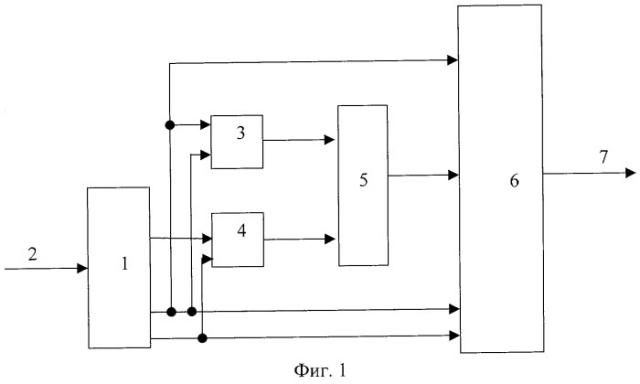
Функциональная схема устройства представлена на фиг.1. Она включает: регистр1, вход 2, первый блок вычисления синдрома ошибки 3, второй блок вычисления синдрома ошибки 4, блок памяти 5, сумматор 6, выход 7.
Устройство работает следующим образом.
На вход 2 устройства подается контролируемое число, представленное в полиномиальной форме:
где αi(z) - остаток A(z) по модулю Pi(z); Pi(z),..., Pn(z) - рабочие основания; Pn+1(z), Pn+2(z) - контрольные основания.
Данный вектор A(z)=(α1(z), α2(z),..., αn(z), αn+1(z), αn+2(z) записывается в регистр 1. На вход первого блока вычисления синдрома ошибки 3 с выходов регистра 1 подается:
С образованием на его выходе сигнала:
При этом:
α* n+1(z)=λ(1) 1α1(z)+λ(1) 2α2(z)+...+λ(1) nαn(z),
где λ(1) 1 - константы системы.
На входы второго блока вычисления синдрома ошибки 4 с выходов регистра 1 подается:
С образованием на выходе сигнала:
При этом:
α* 2(z)=λ(2) 1α1(z)+λ(2) 2α2(z)+...+λ(2) nαn(z),
где λ(2) 1 - константы системы.
Величины δ1(z) и δ2(z) в двоичном виде поступают на входы блока 5 памяти и выбирают оттуда соответствующую константу ошибки. Эта константа ошибки поступает в сумматор 6, где суммируется с искаженным A(z), представленный вне позиционном виде, из регистра 1 исправленное представление A(z) с выхода сумматора 6 подается на выход 7 устройства.
В качестве примера рассмотрим расширенное поле Галуа GF(24), в котором определены следующие основания:
P1(z)=z+1
P2(z)=z2+z+1
P3(z)=z4+z3+z2+z+1,
где P1(z), P2(z) и Р3(z) - рабочие основания,
P4(z)=z4+z3+1
P5(z)=z4+z+1,
а P4(z) и P5(z) - контрольные основания.
Имеем:
B1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1,
B2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z,
B3(z)=z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z,
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3,
B5(z)=z12+z9+z8+z6+z4+z3+z2+z,
Bраб(z)=z7+z6+z5+z2+z+1,
Тогда,
B1(z)=(z7+z4+z2+z) Рраб(z)+z6+z4+z3+z2+1,
B2(z)=(z7+z5+z2+z+1) Рраб(z)+z6+z5+z+1,
B3(z)=(z7+z4+z3+z+1) Рраб(z)+z5+z4+z3+z2+z+1,
B4(z)=(z7+z4+z3) Рраб(z),
B4(z)=(z5+z4+z) Рраб(z).
Если полином A(z) Рраб, то справедливо:
(α1(z), α2(z), α3(z))=(α1(z), α2(z), α3(z), α4(z), α5(z)),
где левая часть равенства представлена по рабочим основаниям P1(z), P2(z), Р3(z), а правая - по полиномной системе оснований P1(z), P2(z), Р3(z), P4(z), P5(z) расширенного поля Галуа GF(24).
Тогда согласно китайской теореме об остатках
Следовательно,
и
где B* i(z) - ортогональные базисы без избыточной системы класса вычетов по основаниям P1(z), Р2(z), Р3(z).
Исходя из условия, что α1(z) представляется в виде двоичного позиционного кода, то выражение (7) и (8) можно представить в виде:
и
где αk i - значения k-го разряда i-го остатка; k=0, 1, ord pi(z)-1; ord Рi(z) - степень i-го основания в ПСКВ.
Значения констант и представлены в таблице 1.
| Таблица 1 | ||
| Значения αk i(z) | Основания | |
| P4(z)=z4+z3+1 | P5(z)=z4+z+1 | |
| α0 1(z) | z3+z+1 | z |
| α0 2(z) | z2+z+1 | z3+1 |
| α1 2(z) | z3+z | z2+z+1 |
| α0 3(z) | z3+z2+1 | z3+z |
| α1 3(z) | z+1 | z2+z+1 |
| α2 3(z) | z | z3 |
| α3 3(z) | z2 | z+1 |
Тогда разность между вычисленными значениями α* 4(z) и α* 5(z), согласно (2), и остатками полинома A(z), принадлежащих α4(z) и α3(z) по контрольным основаниям P4(z) и P5(z) образуют синдром ошибки.
δ1(z)≡α4(z)-a* 4(z)mod P4(z)
δ2(z)≡α5(z)-a* 5(z)mod P5(z)
Таким образом, первый блок вычисления синдрома ошибки реализует процедуру
Второй блок вычисления синдрома ошибки реализует процедуру
Если δ1(z)=0 и δ2(z)=0, то не позиционное представление полинома A(z) не содержит ошибки. В противном случае по величинам δ1(z) и δ2(z) определяется местоположение и глубина ошибки. Пусть дан полином A(z)=(1, z+1, z3+z2+z+1, z3+z2+1, z3+z). Определим свертку:
α* 4(z)=z3+z2+1
α* 5(z)=z3+z
Определим синдром ошибки:
δ1(z)≡((z3+z2+1)+(z3+z2+1))mod P4(z)=0
δ2(z)≡((z3+z)+(z3+z))mod P5(z)=0
Следовательно, исходная комбинация (1, z+1, z3+z2+z+1, z3+z2+1, z3+z) не содержит ошибки. Блок памяти будет содержать следующие константы ошибок:
| Таблица 2 | |||
| Основание | Ошибка | δ1(z) | δ2(z) |
| P1(z)=z+1 | 1 | z3+z+1 | z |
| P2(z)=z2+z+1 | 1 | z2+z+1 | z3+1 |
| z | z3+z | z2+z+1 | |
| P3(z)=z4+z3+z2+z+1 | 1 | z3+z2+1 | z3+z |
| z | z+1 | z2+z+1 | |
| z2 | Z | z3 | |
| z3 | z2 | z+1 |
Пусть на вход 2 устройства подается контролируемое значение:
A(z)=(1, z+1, z2+z+1, z3+z2+1, z3+z)
Тогда, согласно выражениям (9) и (10) получаем:
α* 4(z)=z2+1
α* 5(z)=z3
Определяем синдром ошибки:
δ1(z)≡(z3+z2+z+z2+1)mod(z4+z3+1)=z3+z+1
δ2(z)≡(z3+z+z3)mod(z4+z+1)=z
Из блока памяти 5 в соответствии с δ1=z3+z+1 и δ2=z выбирается величина (1, 0, 0), которая складывается с контролируемым числом в сумматоре 6 с образованием на выходе:
(1, z+1, z2+z+1, z3+z2+z, z3+z)+(1,0,0,0,0)=(0, z+1, z2+z+1, z3+z2+z, z3+z).
Заметим, что если A(z) не будет содержать ошибки, то величины синдрома δ1 и δ2 равны нулю. Использование в предлагаемом изобретении двух блоков 3 и 4 вычисления синдрома ошибки позволяет упростить устройства, т.к. данные блоки выполняют функцию блока модульной свертки модульного сумматора по каждому контрольному основанию. Кроме того, использование двухслойной сети и совмещение процедур вычисления α* 4(z)(α* 4(z)) и δ1(z)(δ2(z)) позволяет увеличить быстродействие устройства.
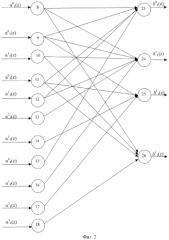
Блок вычисления синдрома ошибки по модулю P4(z)=z4+z3+1 представлен на фиг.2. Он представляет собой двухслойную нейронную сеть.
Первый слой содержит 11 нейронов. На входы нейронов 8, 9-10, 11-14 в двоичном виде поступают остатки α1(z), α2(z), α3(z) по рабочим основаниям P1(z), P2(z), Р3(z). На нейроны 15-18 поступает двоичный код α4(2) по модулю P4(z)=z4+z3+1.
Второй слой нейронной сети содержит 4 нейрона выполняющих базовую операцию суммирования по модулю 2, причем первый нейрон 2 слоя 23 связан с выходами 8, 9, 11, 12 и 15 нейронов 1 слоя. Нейрон 2 слоя 24 связан с выходами 8, 9, 10, 12, 13 и 16 нейронов 1 слоя, нейрон 2 слоя 25 связан с выходами 9, 11, 14 и 17 нейронов 1 слоя, а соответственно нейрон 2 слоя 26 связан с выходами 8, 10, 11 и 18 нейронов 1 слоя.
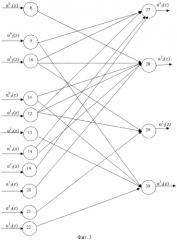
Блок вычисления синдрома ошибки по модулю P5(z)=z4+z+1 представлен на фиг.3. Он представляет собой двухслойную нейронную сеть.
Первый слой содержит 11 нейронов. На входы нейронов 8, 9-10, 11-14 в двоичном виде поступают остатки α1(z), α2(z), α3(z) по рабочим основаниям P1(z), P2(z), Р3(z). На нейроны 19-22 поступает двоичный код α5(z) по модулю P4(z)=z4+z+1.
Второй слой нейронной сети содержит 4 нейрона выполняющих базовую операцию суммирования по модулю 2, причем первый нейрон 2 слоя 27 связан с выходами 9, 10, 12, 14 и 19 нейронов 1 слоя. Нейрон 2 слоя 28 связан с выходами 8, 10, 11, 12, 14 и 20 нейронов 1 слоя, нейрон 2 слоя 29 связан с выходами 10, 12 и 21 нейронов 1 слоя, а соответственно нейрон 2 слоя 30 связан с выходами 9, 11, 13 и 22 нейронов 1 слоя.
Устройство для обнаружения и исправления ошибок в полиномиальной системе класса вычетов, содержащее регистр, вход которого является входом устройства, блок памяти и выходной сумматор, первый, второй и третий входы которого соединены соответственно с первым, вторым и третьим выходами регистра, а четвертый вход соединен с выходом блока памяти, отличающееся тем, что содержит два блока вычисления синдрома ошибки по контрольным основаниям, причем первый выход регистра соединен с первыми входами блоков вычисления синдрома ошибки, а второй и третий выходы регистра подключены соответственно ко вторым выходам первого и второго блоков вычисления синдрома ошибки, выходы которых подключены к входам блока памяти, причем первый блок вычисления синдрома ошибки выполнен на двухслойной нейронной сети и содержит в первом слое 11 нейронов, на входы которых подаются в двоичном виде остатки по трем рабочим и одному контрольному основаниям, второй слой нейронной сети содержит 4 нейрона, выполняющих базовую операцию суммирования по модулю 2, входы первого нейрона второго слоя соединены с выходами 1, 2, 4, 5 и 8 нейронов первого слоя, входы второго нейрона второго слоя соединены с выходами 1, 2, 3, 5, 6 и 9 нейронов первого слоя, входы третьего нейрона второго слоя соединены с выходами 2, 4, 7 и 10 нейронов первого слоя, входы четвертого нейрона второго слоя соединены с выходами 1, 3, 4 и 11 нейронов первого слоя, выходы нейронов второго слоя являются выходами первого сумматора, второй блок вычисления синдрома ошибки выполнен на двухслойной нейронной сети и содержит в первом слое 11 нейронов, на входы которых подаются в двоичном виде остатки по трем рабочим и второму контрольному основаниям, второй слой нейронной сети содержит 4 нейрона, выполняющих базовую операцию суммирования по модулю 2, входы первого нейрона второго слоя соединены с выходами 2, 3, 5, 7 и 8 нейронов первого слоя, входы второго нейрона второго слоя соединены с выходами 1, 3, 4, 5, 7 и 9 нейронов первого слоя, входы третьего нейрона второго слоя соединены с выходами 3, 5 и 10 нейронов первого слоя, входы четвертого нейрона второго слоя соединены с выходами 2, 4, 6 и 11 нейронов первого слоя, выходы нейронов второго слоя являются выходами второго блока вычисления синдрома ошибки.