Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов

Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано в процессорах обработки сигналов, в цифровых фильтрах.

Известно отказоустойчивое устройство для вычисления сумм парных произведений в системе классов вычетов - системе остаточных классов (патент РФ №2012041, кл. G 06 F 7/72, 1994 г.), содержащее входной регистр, блок коррекции ошибки, модульный сумматор, блок вычисления сумм парных произведений, блок памяти, матричный умножитель, счетчик тактов, матричный умножитель.

Недостатком данного устройства является низкое быстродействие и большой объем оборудования, вследствие использования для вычисления интервального номера числа коммутатора, одного ПЗУ и двух умножителей.

Основной задачей, на решение которой направлено заявляемое устройство, является сокращение аппаратных затрат, увеличение быстродействия.

Техническим результатом, достигнутым при осуществлении заявленного изобретения, является повышение скорости обнаружения и коррекции ошибок и снижение объема оборудования.

Указанный технический результат достигается за счет применения полиномиальной системы классов вычетов (ПСКВ), в которой в качестве основания системы используются минимальные многочлены p_i(z), i= 1, 2,..., n, определенные в расширенных полях Галуа GF(2^ν) и нейросетевых технологий.

Сущность изобретения заключается в следующем. Основным достоинством полиномиальной системы классов вычетов (ПСКВ) является независимость образования разрядов числа, в силу чего каждый разряд несет информацию обо всем исходном числе. Отсюда вытекает возможность их параллельной обработки. Это позволяет привлечь новые методы арифметического контроля. При введении дополнительного контрольного основания остаток, взятый по этому основанию, несет избыточную информацию об исходном полиноме, что позволяет обнаружить и исправить ошибки в цифрах по рабочим основаниям.

Любое число N, выраженное в двоичном коде, можно представить в полиномиальной форме. Тогда полученный полином N(z) представляется в ПСКВ как набор остатков (α₁(z), α₂(z)...α_n(z), α_n+1(z)), где α_i(z)=rest(N(z)/p_i(z)); p_i(z) - минимальный многочлен, определяемый в расширенном поле Галуа GF(p^ν). Согласно китайской теореме об остатках

где В_i(z) - ортогональные базисы; r(z) - ранг N(z).

Тогда значение полного диапазона определяется равенством (2)

где p_i(z) - основания ПСКВ i=1, n+1; n(z) - число рабочих оснований; р_n+1 (z) - контрольное основание.

В тоже время

где P(z) - рабочий диапазон.

Полином N(z) считается правильным, если N(z)∈P(z). Другими словами

где S(z) - полиномиальная форма интервала; P(z) - рабочий диапазон.

Подставим в равенство (4) равенство (1), тогда

Известно, что B_i(z)=R_i(z)P(z)+A_i(z),

A_i(z)=rest(B_i(z)/P(z)).

Ho A_i(z)=B_i*(z) - ортогональный базис безызбыточной системы с основаниями p₁(z), p₂(z), ...p_n(z).

Полученные равенства подставляем в формулу (5), тогда

Тогда по величине S можно однозначно определить величину Δ коррекции результата. Например, пусть имеем поле Галуа GF(p³), в котором определены минимальные многочлены, составляющие систему оснований ПСКВ p₁(z)=z+1, p₂(z)=z³+z²+1, p₃(z)=z³+z+1 (контрольное основание р₃(z)).

Тогда

Вычислим ортогональные базисы

B₁(z)=z⁶+z⁵+z⁴+z³+z²+z+1

B₂(z)=z⁶+z⁵+z³+1

B₃(z)=z⁴+z²+z+1

Вычислим коэффициенты

B₁(z)=(z²+z)P(z)+(z³+z²+1)

B₂(z)=(z²+z+1)P(z)+(z³+z²)

B₃(z)=1P(z)

Тогда

B₁(z)=R₁ P(z)+B₁*

B₂(z)=R₂P(z)+B₂*

B₃(z)=R₃P(z)

Получаем систему безызбыточных оснований p₁(z)=z+1, p₂(z)=z₃+z₂+1, в которой определены ортогональные базисы, B₁*(z)=z³+z²+1, B₂*(z)=z³+z².

Определим интервальный номер

Тогда

Возьмем N(z)=z². В ПСКВ данный полином имеет вид N=(0, z, z²).

Вычислим значение интервального полинома

Тогда истинное значение полинома определяется следующим образом

N(z)→N(z)=N*(z)+Δα_i(z)B_i(z),

где N*(z) - значение полинома, поступившего на вход устройства.

Пусть ошибка произошла по первому основанию.

Тогда N*(z)=(1, z, z²)

Тогда, согласно выражению (1)

Тогда N(z)=N*(z)+Δ=z⁶+z⁵+z⁴+z⁶+z⁵+z⁴+z³+z²+z+1=z³+z²+z+1

Глубина ошибки по основаниям и корректирующие значения Δ на выходе элемента памяти приведены в таблице 1.

Таблица 1
Основание	Глубина ошибки	Величина S на входе памяти	Значения Δ на выходе памяти
P1(z)	1	z2+z	z6+z5+z4+z3+z2+z+1
P2(Z)	1	z2+z+1	z6+z5+z3+1
	z	z2	z6+z4+z+1
	z+1	z+1	z5+z4+z3+z

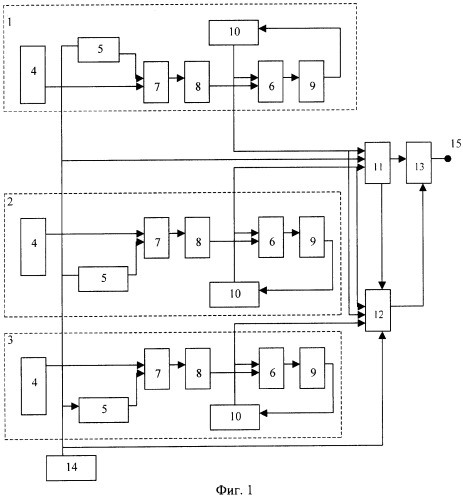
На фиг.1 представлена функциональная схема отказоустойчивого устройства для вычисления сумм парных произведений, а на фиг.2 - функциональная схема блока коррекции ошибки.

Отказоустойчивое устройство для вычисления сумм парных произведений (фиг.1) содержит блоки вычисления парных произведений по произвольному модулю 1, 2 и по контрольному модулю 3, каждый из которых содержит регистр 4, память 5, матричный сумматор 6, матричный умножитель 7 и три группы буферных регистров 8, 9, 10, преобразователь 11 кода ПСКВ в позиционный код, блок 12 коррекции ошибки, модульный сумматор 13, счетчик 14 тактов и выход 15 результата устройства.

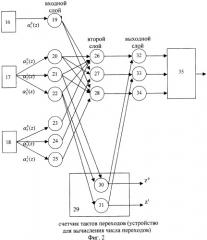
Блок 12 коррекции ошибки представляет собой многосложную нейронную сеть прямого распространения. Блок 12 коррекции ошибки (фиг.2) содержит три регистра 16-18, первый слой нейронной сети из 7 нейронов 19-25, трех нейронов 26-28 второго слоя сети, счетчика тактов переходов 29, содержащего два нейрона 30 и 31, и трех нейронов 32-34 выходного слоя и блок памяти 35.

Устройство работает следующим образом. В информационные регистры 4 блоков 1, 2, 3 до начала работы записаны числа в коде ПСКВ. Счетчик тактов формирует адреса для считывания коэффициентов, которые хранятся в блоках 1, 2, 3 в памяти 5 в коде ПСКВ. Содержание регистров 4 в каждом из блоков 1, 2, 3 перемножается с коэффициентами с помощью матричных умножителей 7. Результат умножения записывается в первую группу буферных регистров 8, содержимое которых складывается с содержимым буферных регистров 10 третьей группы (в первом цикле происходит сложение с нулем). Сложение осуществляют матричные сумматоры G в каждом из блоков 1, 2, 3. Сумма записывается в буферные регистры 10 третьей группы.

С выходов буферных регистров 10 блоков 1, 2 результат подается на входы преобразователя 11 кода ПСКВ в позиционный код и на информационные входы блока 12 коррекции ошибки, на третий вход которого подается также информация с выходов буферных регистров 10 блока 3. Счетчик тактов по окончании суммирования парных произведений выдает разрешающий сигнал на вход разрешения преобразователя 11 и блока 12 коррекции ошибки. Со второго выхода преобразователя 11 на четвертый вход блока 12 коррекции ошибки поступает сигнал о переходе через P(z). Структура преобразователя 11 аналогична прототипу. Результаты с выходов преобразователя 11 кода ПСКВ в позиционный код и блока 12 коррекции ошибки подается на входы модульного сумматора 13, где и происходит сложение.

Выход модульного сумматора 13 является выходом 15 устройств. Слагаемые кода ПСКВ в информационные регистры 4 блоков 1, 2, 3 могут быть записаны из аналого-цифрового преобразователя.

Блок коррекции 12 работает следующим образом. Конечный результат выполнения операции сумм парных произведений в полиномиальной форме в виде остатков α₁(z), α₂(z), α₃(z) подается соответственно на регистры 16, 17, 18, с выхода которых в параллельном коде эти остатки поступают на соответствующие нейроны 19-25 первого слоя нейронной сети. Структура данного слоя имеет архитектуру 1-3-3.

Нейроны данного слоя в процессе вычисления значения интервального номера S(z) не участвуют, а осуществляют перераспределения данных на нейроны второго слоя 26-28 и нейроны 30, 31 счетчика тактов перехода 29. Синаптические веса связей равны "1". Структура связей первого и второго слоев нейронной сети представлена в таблице 2.

Таблица 2
Разряды остатка αi(z)	Номер нейрона	Синаптические связи с нейронами 2-го слоя
		26	27	28
α0 1(z)	19	-	1	1
α0 2(z)	20	1	1	1
α1 2(z)	21	1	-	1
α2 2(z)	22	1	-	-
α0 3(z)	23	1	-	-
α1 3(z)	24	-	1	-
α2 3(z)	25	-	-	1

Нейроны 26-28 второго слоя нейронной сети и нейроны 30-31 счетчика тактов перехода реализуют базовую операцию суммирования по модулю два могут быть довольно легко реализованы на персептроне.

Полученный результат

с выхода нейронов 26-28 в параллельном двоичном коде и значение числа переходов за диапазон P(z) с выходов нейронов 30 и 31 подаются на входы нейронов 32-34 выходного слоя нейронной сети. Синоптические веса связей данных нейронов равны единице и определяются согласно таблице 3.

Таблица 3
Нейроны второго слоя	Синоптические веса нейронов
	нейрон 32	нейрон 33	нейрон 34
26	1	-	-
27	-	1	-
28	-	-	1
30	1	-	-
31	-	1	-

Нейроны 32-34 выходного слоя нейронной сети реализуют базовую операцию суммирования по модулю два. С выхода нейронов 32-34 выходного слоя нейронной сети значения интервального номера S(z) в параллельном двоичном коде поступают на вход памяти 35, на выходе которой появляется значение коррекции, которое подается на выход блока коррекции ошибки.

Устройство для вычисления сумм парных произведений, содержащее преобразователь кода полиномиальной системы класса вычетов (ПСКВ) в позиционный код, счетчика тактов и два блока вычисления парных произведений по произвольному основанию, каждый из которых содержит регистр, память, матричный умножитель, три группы буферных регистров и матричный сумматор, причем выход счетчика тактов соединен с адресными входами памяти первого и второго блоков вычисления сумм парных произведений по произвольному основанию и входами разрешения работы преобразователя кода ПСКВ в позиционный код, а в каждом из блоков вычисления сумм парных произведений по произвольному модулю выход регистра соединен с первым входом матричного умножителя, второй вход которого соединен с выходом памяти, а выходы - с входами буферных регистров первой группы, выходы которых соединены с выходами первого слагаемого матричного сумматора, выходы которого соединены со входами буферного регистра второй группы, выходы которого соединены со входами буферного регистра третьей труппы, выходы которого соединены с входами второго слагаемого матричного сумматора и соответственно с первым и вторым информационными входами преобразователя ПСКВ в позиционный код, отличающееся тем, что в него введены блок коррекции ошибки, модульный сумматор и блок вычисления сумм парных произведений по контрольному основанию, состоящий из регистра, памяти, матричного умножителя, матричного сумматора и трех групп буферных регистров, причем выход счетчика тактов соединен с адресным входом памяти блока вычисления сумм парных произведений по контрольному основанию и входом разрешения работы блока коррекции ошибки, выход которого соединен с входом первого слагаемого модульного сумматора, вход второго слагаемого которого соединен с первым выходом преобразователя кода ПСКВ в позиционный код, а выход - с выходом результата устройства, а в блоке вычисления сумм парных произведений по контрольному основанию выход регистра соединен с первым входом матричного умножителя, второй вход которого соединен с выходом памяти, а выход - с входами буферных регистров первой группы, выходы которых соединены с входами первого слагаемого матричного сумматора, выходы которого соединены с входами буферных регистров второй группы, выходы которых соединены с входами буферных регистров третьей группы, выходы которых соединены с входами второго слагаемого матричного сумматора и первым информационным входом блока коррекции ошибки, вторые и третьи информационные входы которого соединены соответственно с выходами буферных регистров третьей группы первого и второго блоков вычисления сумм парных произведений по произвольному основанию, блок коррекции ошибки содержит три регистра, семь нейронов входного слоя, предназначенных для осуществления перераспределения данных на три нейрона второго слоя и два нейрона счетчика тактов перехода, выходы которых соединены со входами трех нейронов выходного слоя, нейроны второго слоя, нейроны счетчика тактов перехода и нейроны выходного слоя предназначены для реализации базовой операции суммирования по модулю два, причем выход первого регистра соединен со входом первого нейрона входного слоя, выход второго регистра соединен со входами второго, третьего и четвертого нейронов входного слоя, выход третьего регистра соединен со входами пятого, шестого и седьмого нейронов входного слоя, а выходы первого нейрона входного слоя соединены с вторым и третьим нейронами второго слоя, выходы второго нейрона входного слоя соединены с первым, вторым и третьим нейроном второго слоя, выходы третьего нейрона входного слоя соединены с первым и третьим нейроном второго слоя и первым нейроном счетчика тактов переходов, выходы четвертого нейрона входного слоя соединены с первым нейроном второго слоя и первым и вторым нейроном счетчика тактов перехода, выход пятого нейрона входного слоя соединен с входом первого нейрона второго слоя, выход шестого нейрона входного слоя соединен с входом второго нейрона второго слоя, выход седьмого нейрона входного слоя соединен со входом третьего нейрона второго слоя, выход первого нейрона второго слоя и выход первого нейрона счетчика тактов переходов соединены со входами первого нейрона выходного слоя, выход второго нейрона второго слоя и выход второго нейрона счетчика тактов перехода соединены со входами второго нейрона выходного слоя, выход третьего нейрона второго слоя соединен со входом третьего нейрона выходного слоя, выходы первого, второго и третьего нейрона выходного слоя соединены с входом блока памяти.