Проверяемые секретные перетасовывания и их применение при проведении электронного голосования
Иллюстрации
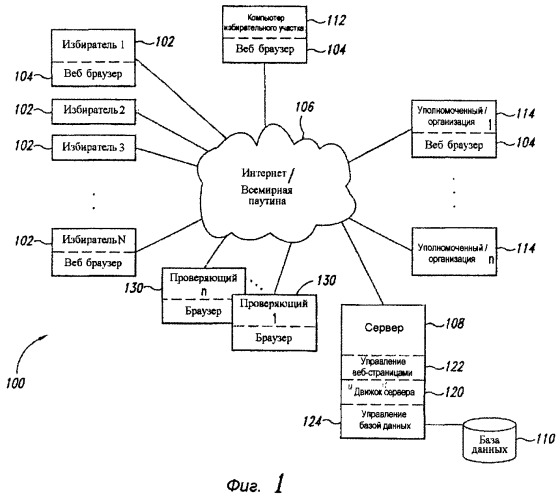
Показать всеИзобретение относится к системам голосования, в которых используется повсеместно проверяемый протокол проведения голосования. Техническим результатом является повышение эффективности голосования. Система содержит сервер и, по меньшей мере, три компьютера избирателей, соединенных с вычислительной сетью. Компьютер первого избирателя выполнен с возможностью перетасовывания полученных электронных мандатов и выработки первого доказательства правильности для первого набора перетасованных мандатов. Компьютер второго избирателя выполнен с возможностью перетасовывания первого набора перетасованных мандатов и выработки второго доказательства правильности для второго набора перетасованных мандатов. Компьютер третьего избирателя выполнен с возможностью перетасовывания второго набора перетасованных мандатов и выработки третьего доказательства правильности для третьего набора перетасованных мандатов. Сервер выполнен с возможностью получения указанных доказательств и проверки и подсчета голосов. 8 н. и 29 з.п. ф-лы, 2 ил.
Реферат
Понятие о перетасовывании системы объектов, записей или ярлыков является простым и интуитивно понятным и примеры тасования в большом количестве окружают нас в различных повседневных ситуациях. Игрок в казино знает, что среди карт в его руке, каждая является одной из 52 возможных различных карт, и что ни у кого за столом не будет такой же карты, какая есть у него. Тем не менее, он ничего не знает о том, как распределены карты, даже если он записывает точный порядок карт до того, как их перетасовывает крупье.
Применительно к электронным данным, задача получения случайной перестановки (но действие которой можно проверить) входной последовательности является очень сложной. Проблема состоит в том, что сами данные либо видимы проверяющему, либо нет. Если они видимы, то проверяющий или другой наблюдатель может легко восстановить соответствие между входными и выходными записями. Если данные не видны, то входные и выходные записи должны являться разными представлениями одних и тех же исходных данных. Но, если выход достаточно сильно отличается от входа (то есть, является результатом процесса «хорошего» шифрования) и проверяющий не может восстановить упомянутое выше соответствие, то, как может проверяющий быть уверенным, что тот, кто тасовал данные, не изменил исходные данные в процессе перетасовывания?
Большинство статей посвящены разработке эффективного (линейного) способа решения данной задачи в одной важной ситуации - данные зашифрованы с помощью алгоритмов Эль-Гамаля или Диффи-Хеллмана. Для того чтобы сделать изложение как можно более ясным и четким, большая часть статей открыто обращается к конкретному случаю, когда операции выполняются в простой подгруппе группы Zp* - мультипликативной группы вычетов по модулю большого простого числа р. Тем не менее, единственным свойством исходной (мультипликативной) группы, которым мы пользуемся, является то, что соответствующая проблема Диффи-Хеллмана трудноразрешима. Таким образом протокол перетасовывания также применим в случае, когда криптосистема Эль-Гамаля строится для других групп, таких как группы эллиптических кривых.
Общие булевские методы доказательства из работ [1] и [4] можно также использовать для построения доказательства с аналогичными свойствами, тем не менее, итоговый размер доказательства (сложность) будет являться квадратичной (или более сложной) функцией от размера входной последовательности.
Способ согласно данной работе также имеет некоторые преимущества по сравнению с методом «разрезать и выбрать», использованном в работе [8]. В данном подходе размер доказательства зависит от вероятности мошенничества, доказывающего, что данная вероятность необходима для того, чтобы убедить всех участников. В протоколе перетасовывания согласно данной работе упомянутая вероятность мошенничества по существу равна k/q, где k - число тасуемых элементов, a q - мощность подгруппы из Zp*, в которой элементы подвергаются шифрованию. Хотя в [8] не проанализирована зависимость размера доказательства от вероятности мошенничества, кажется, что для получения подобной малой вероятности обмана необходимо, чтобы данный размер был на порядки больше размера доказательства, данного в этой работе. (Более того, если протокол из работы [8] работает не в диалоговом режиме, то вероятность мошенничества необходимо выбирать очень маленькой, так как злоумышленник может использовать значительные автономные вычислительные мощности для подбора поддельного доказательства с помощью полного перебора. Это же, конечно, может случиться и с протоколом из данной работы, но вероятность k/q является достаточно небольшой величиной для всех применяемых на практике значений k и q - даже для автономных атак).
Результаты данной работы предусматривают несколько путей реализации повсеместно проверяемого протокола проведения голосования. Некоторые из этих путей представлены в заключительных разделах работы. В этой связи целесообразно сравнить данный протокол с «элегантным гомоморфным протоколом проведения голосования» из работы [2]. Упомянутый протокол хорошо работает в ситуации, когда бюллетени содержат только простые вопросы типа «выберете (не более) m из n». Данные вопросы исключают ответы, где надо что-то вписывать свое, аналогичным свойством обладают вопросы «пропорционального типа», когда предполагается, что голосующий отмечает ответы в порядке своих предпочтений и вопросы сводятся в таблицы в соответствии с этими предпочтениями. (Теоретически вопросы пропорционального типа можно обрабатывать следующим образом: сопоставлять каждой возможной перестановке вариантов ответов единственный ответ - да или нет. Тем не менее, на практике данный вариант не осуществим, за исключением случаев, когда количество вариантов выбора ответа достаточно мало). Пара несколько менее важных недостатков схемы из [2] заключаются в том, что она значительно увеличивает размеры данных голосования и эта схема подразумевает наличие доказательства подлинности голосующего. Данное доказательство еще больше увеличивает размеры данных голосования примерно на порядок и оно не является привлекательным исходя из практических соображений, так как подразумевает, что на компьютере голосующего будет выполняться специальная программа.
Протоколы перетасовывания данной работы целиком построены на элементарных арифметических операциях. Следовательно, их легко реализовать и они хорошо пригодны для описанного здесь приложения с анонимными мандатами.
Применение к голосованию
Немедленно приходящее на ум применение к вопросу голосования заключается в использовании описанных протоколов для реализации обычного подхода центра сведения/перемешивания данных в вопросе обеспечения анонимности. В этом случае протоколы данной работы имеют несколько важных преимуществ. Они очень эффективны и позволяют центрам перемешивания данных быть полностью независимым от властей, которые обладают некоторой частью ключа, необходимого для расшифрования бюллетеней.
Тем не менее, возможно более ценным и интересным является применение нового протокола для создания «анонимных мандатов». Член некоторой группы лиц, определяемой только с помощью нескольких открытых ключей алгоритмов DSA или Диффи-Хеллмана, может подтвердить членство в упомянутой группе и/или поставить свою одноразовую подпись, при этом все действия проделываются, не раскрывая своей личности. Это приводит к новому решению задачи голосования, при этом решение можно будет везде проверить, но оно не предполагает наличия некоторого специального множества «уполномоченных лиц», которые осуществляют сведение результатов. Также новый протокол подразумевает модель большей конфиденциальности голосующего и значительно ускоряется сведение результатов, так как отпадает необходимость зашифровывать/расшифровывать бюллетени. В сущности, вместо перемешивания зашифрованных данных голосования после получения бюллетеней в центре сбора данных голосования, мандаты голосующих смешиваются до начала проведения выборов. На самом деле упомянутое перемешивание могут проводить сами голосующие с целью «анонимной идентификации» (смотри раздел 7.1). (Заметим, что смешивание может также проводиться несколькими уполномоченными лицами, таким образом обеспечивается более эффективное средство для внедрения голосования с пороговой секретностью. При таком голосовании снова не нужно зашифровывать/расшифровывать бюллетени).
Обозначения
Далее, если не оговорено другое, n - это положительное целое число, р и q - известные простые числа. Арифметические операции производятся в кольце вычетов Zp (или иногда Zn) и g ∈ Zp - число, мультипликативный порядок которого (простое число) равен q. (Очевидно, что q|(р-1)). В каждом протоколе доказательства через Р обозначаем того, кто доказывает (тасующего) и через V-проверяющего (того, кто контролирует).
Напомним доказательство Чаума-Педерсена знания равенства для дискретных логарифмов. Для G, X, Н, Y ∈ Zp это является доказательством знания соотношения
Известно, что данный протокол является протоколом с нулевым разглашением, тем не менее, он известен как протокол с нулевым разглашением при честном проверяющим. В следующем разделе приведем естественное обобщение данного протокола на несколько переменных и данный обобщенный протокол также будет обладать указанными свойствами. Этих свойств достаточно для нашего основного приложения, в котором проверяющий осуществляется с помощью эвристики Фиата-Шамира (Смотри [5] и [2]). Определение 1. Данное доказательство, как и выше, обозначается через CP(G, X, Н, Y). Определение 2. Для фиксированного g ∈ Zp*, обозначим через ⊗g бинарный оператор, действующий на (g)×(g), определяемый следующим образом:
logg (x ⊗gy)=loggx loggy
для всех x, у ∈ (g). Или, по-другому:
ga⊗ggb=gab=(ga)b=(gb)a
для всех a, b ∈ Zp. Следуя соглашениям, используемым для сумм и произведений, также будем использовать обозначение
Будем называть данный оператор логарифмическим произведением с основанем g.
При каждом использовании обозначения из данного выше определения, нижний индекс g можно не писать, если его значение ясно из контекста.
Замечание 1. Заметим, что
Приведем ниже ряд хорошо известных результатов, которые будем активно использовать в оставшейся части работы.
Лемма 1. Пусть f(x) ∈ Zq[x] - многочлен степени d. Тогда существует не более d значений z1, z2,..., zd ∈ Zq таких, что f(zi)=0.
Следствие 1. Пусть f(x), g(x) ∈ Zg[x] - два многочлена степени не выше d, причем f≠g. Тогда существует не более d-1 значения z1, z2,..., Zd-1 ∈ Zq таких, что f(zi)=g(zi).
Следствие 2. Пусть f(x), g(x) ∈ Zq[x] - два многочлена степени не выше d, причем f≠g. Если t ∈R Zq (t выбирается случайно из Zq), то
P({t:f(t)=g(t)})≤(d-1)/q.
Следствие 3. Пусть f(x), g(x) ∈ Zg[x] - любые два многочлена степени не выше d. Тогда для каждой константы R ≠ 0, существует не более d значений z1(R),..., zd(R) таких, что f(zi(R))=Rg(zi(R)).
Определение 3. Пусть f(x) - многочлен из Zg[x]. Обозначим через χf (неупорядоченное) множество всех корней многочлена f, то есть по определению
Определение 4. Если Λ ⊂ Zg и R ∈ Zg, то по определению пишем
Следствие 4. Пусть f(x), g(x)∈Zg[x] - любые два многочлена степени не выше d.
Зафиксируем константы R≠0, γ≠0 и δ≠0. Если t ∈R Zq, то
P({t:f(γt)=Rg(δt)})≤d/q.
Лемма 2. Пусть Zk q - стандартное векторное пространство над Zq размерности k и fix ν=(ν1,...,... νk) ∈ Zk q, ν≠0 и а ∈ Zq. Если r ∈R Zk q выбирается случайно, то
P({r:ν·r=a})=1/q.
Доказательства для повторного логарифмического умножения
До конца данного раздела все логарифмические умножения будут вычисляться относительно фиксированного элемента g и таким образом будем опускать нижний индекс g в обозначениях. Задача, описанная далее, является принципиальной для протоколов перетасовывания, которые будут описаны позже.
Задача повторного логарифмического умножения: Две последовательности {Хi)k i=1 и {Yi}k i=1 известны. Доказывающий Р также знает ui=logg Xi и νi=logg Yi, для всех i, но данные последовательности не известны проверяющему V. Доказывающему Р необходимо убедить V в том, что
при этом Р не должен раскрывать никакой информации о секретных числах ui и νi.
Протокол, представленный ниже, является в точности обобщением на большую размерность протокола Чаума-Педерсена, упомянутого в начале раздела 2. На самом деле, мы увидим, что в случае k=2 данный протокол является непосредственно протоколом Чаума-Педерсена. Описание будет значительно проще, если мы ограничим описание протокола случаем, когда
Ясно, что если какое-либо из приведенных неравенств не выполняется, то бессмысленно строить доказательство, так как выполнение или невыполнение равенства (5) можно легко проверить. (Если Хi=1, то хi=0 и тогда равенство (5) верно тогда и только тогда, когда для некоторого j справедливо Yi=1. Аналогичное верно в случае, когда последовательности X и Y меняются местами).
Протокол доказательства для повторного логарифмического умножения (ПДПЛУ):
1. Р секретно, случайно и равновероятно порождает k-1 элемент из Zq: θ1,..., θk-1. Затем Р вычисляет
и передает проверяющему V последовательность А1,..., Аk.
2. V генерирует случайный элемент γ∈Zq и передает его доказывающему Р.
3. Р вычисляет k-1 элемент из Zq:r1,...,rk-1, удовлетворяющие соотношениям
и передает последовательность r1,..., rk-1 проверяющему V. (Ниже, при доказательстве полноты, мы увидим, каким образом вычисляются данные значения.)
4. Проверяющий V принимает доказательство как правильное тогда и только тогда, когда выполняются соотношения (8).
Теорема 1. ПДПЛУ является трехходовым, с открытой монетой доказательством знания равенства (5), доказательство является с особенным нулевым разглашением при честном проверяющем. Число возведений в степень, необходимое для построения доказательства (то, что делает Р), равно k и число возведений в степень, необходимое для проверки доказательства (то, что делает V), равно 2k. Если V генерирует элементы γ случайно, то вероятность фальсификации при доказательстве равна 1/q.
Замечание 2. Заметим, что при построении доказательства в степень возводится одно число (основание) g и, таким образом, можно применять алгоритмы с фиксированным основанием (смотри [6], стр. 623).
Доказательство. Ясно, что протокол является трехходовым и протоколом с открытой монетой. На первый взгляд кажется, что число возведений в степень при построении доказательства должно равняться 2k-2, но, на самом деле, его можно построить, используя только k возведений в степень. Это объясняется тем, что Р знает числа хi и уi (которые являются логарифмами от Xi и Yi соответственно) и, следовательно, может вычислять Ai по формуле для всех 2≤i≤k-1.
Полнота
Полнота означает, что для произвольных и γ доказывающий Р может всегда найти такой вектор , элементы которого удовлетворяют системе равенств (8). Для того, чтобы убедиться в том, что в нашем случае сказанное имеет место, прологарифмируем по основанию g обе стороны равенств из (8) и положим для всех 1≤i≤k-1. В результате получится следующая система из k линейных уравнений (при записи в матричной форме соответствующая матрица будет иметь размер k×(k-1)) над Zq относительно
Подсистема из последних k -1 уравнений
невырожденная, так как соответствующий определитель равен Пk i=2=xi что не равно нулю благодаря предположению (6). Следовательно, систему уравнений можно решить относительно На самом деле решение записывается следующим образом:
Тем не менее, в предположении данной задачи, выполнение равенства (10) на самом деле следует из справедливости (9). Это происходит благодаря выполнению следующих равенств
что, совместно с фактом, что подматрица из левой части равенства (10) не вырождена, означает, что первый вектор-столбец матрицы размера k × k из (12) должен быть равен линейной комбинации оставшихся k-1 вектор-столбцов.
Корректность
Если первый вектор-столбец матрицы из левой части равенства (12) не является линейной комбинацией оставшихся k-1 вектор-столбцов, то существует не более одного значения γ∈Zq, для которого выполняется равенство (9). Таким образом, если γ выбирается случайно, то существует не более одного шанса из q для того, чтобы Р сгенерировал числа r1,..., rk-1, которые бы убедили проверяющего V в правильности доказательства.
Доказательство с особенным нулевым раскрытием при честном проверяющем
Свойство нулевого раскрытия при честном проверяющем выполняется, потому что для случайного γ и случайного и для
тройка является допустимой для признания доказательства правильным.
Следовательно, имитация строится посредством генерирования случайных и независимых у и ri и вычисления так, как показано в равенстве (13).
Легко видеть, что распределение вектора , построенного описанным выше способом, совпадает с распределением вектора, построенного исходя из (7), снова благодаря тому, что первый вектор-столбец матрицы из (12) является фиксированной линейной комбинацией оставшихся вектор-столбцов. Значит, если проверяющий V ведет себя честно, то имитация пройдет отлично. Следовательно, случайное число γ может выбираться произвольно, мы также имеем выполнение свойства особенного нулевого разглашения при честном проверяющем.
Замечание 3. Выражение для из (11) также может быть формально записано в следующем виде:
Тем не менее, этим выражением нельзя будет воспользоваться, если некоторые из чисел уi будут равны 0. В случае выражения (11) указанная проблема устраняется с помощью введения предположений (6). Конечно, основная часть решения может быть успешно сформулирована в предположении, что уi ≠ 0 для всех 1≤i≤k-1 - только выбор выражения для гi необходимо согласовывать с формой принимаемых предположений.
Замечание 4. Мы оставляем читателю вопрос проверки того, что в случае k=2 протокол ПДПЛУ представляет собой хорошо известный протокол Чаума-Педерсена. При этом желательно вспомнить замечание 1 и равенство (2).
Замечание 5. Особенная корректность
Так же как и в случае протокола Чаума-Педерсена, в котором доказывается, что Р знает s=logG X=logH Y, протокол ПДПЛУ доказывает, что Р знает s1,..., sk такие что loggXi=logg Yi и Пk i=1 si=1. Ясно, что из двух допустимых диалогов и с одинаковым первым шагом, можно выделить свидетельство
(w, ρ)={γ-γ', -'),
удовлетворяющее
Так как w=γ-γ' ≠ 0, то ρi≠0 для всех 1≤i≤k-1. Следовательно, при соответствующей небольшой модификации постановки задачи, протокол будет обладать свойством особенной корректности.
Простое k-перетасовывание
Первый протокол доказательства перетасовывания, который мы опишем, предполагает некоторое количество ограничений. Это будет полезно по двум причинам. Во-первых, этот протокол является базисным структурным элементом для более общего протокола доказательства перетасовывания, который будет описан позже. Также эти ограничения служат второй важной цели. Единственный пример данного доказательства можно построить для того, чтобы по существу «выполнить» преобразование, соответствующее конкретной перестановке. Это может быть важным, когда необходимо тасовать кортежи элементов из Zp, а ведь именно это необходимо при тасовании пар алгоритма Эль-Гамаля как при применении протокола для голосования.
Определение 5. Предположим, что известны две последовательности Х1,..., Хk и Y1,..., Yk элементов из Zp и два дополнительных элемента С и D. Также предположим, что доказывающий Р знает хi=logg Xi и уi=loggYi, с=logg С и d=logg D, но все только что перечисленные значения не известны проверяющему V. Доказывающему Р необходимо убедить V, что существует некоторая перестановка π ∈ Σk, обладающая свойством
для всех 1≤i≤k-1, при этом нельзя раскрывать никакой информации о хi,уi,π, с или d. Будем называть эту задачу Задачей простого k-перетасовывания.
Замечание 6. Для данного раздела и всей оставшейся части данной работы сделаем упрощающие предположения: во всех конструкциях с тасованием
1. хi ≠ xj для i≠j (и, следовательно, уi≠уj для i≠j).
2. хi≠1 для всех 1≤i≤k.
Существуют очевидные пути, каким образом действовать в указанных конкретных случаях. Более того, на практике данные случаи «практически никогда» не встречаются, так как элементы обычно выбираются случайно.
Протокол из предыдущего раздела, совместно со следствием 2, предоставляют «инструменты», необходимые для решения данной задачи фактически прямолинейным способом.
Протокол простого k-перетасовывания:
1. V генерирует случайный элемент t ∈ Zq и передает его Р.
2. Р и V открыто вычисляют U=Dt=gdt, W=Сt=gct,
и
3. Р и V выполняют ПДПЛУ для двух векторов из 2k элементов
Протокол приводит к успеху (V принимает доказательство) тогда и только тогда, когда V принимает ПДПЛУ для данных входных последовательностей.
Теорема 2. Протокол доказательства для простого k-перетасовывания является четырехходовым, с открытой монетой доказательством знания равенства (15). Он удовлетворяет свойству особенной корректности и является протоколом с особенным нулевым разглашением при честном проверяющем. Число возведений в степень, необходимое для проведения доказательства, равно 2k и число возведений в степень, необходимых для проверки доказательства, равно 4k.
Если V генерирует элементы t случайно, то вероятность фальсификации при доказательстве не превосходит
(k-1)/q+(q-k+1)/q2=(qk-q+q-k+1)/q2<k/q.
Замечание 7. Сказанное в замечании 2 также относится к данному случаю.
Доказательство. Все требуемые свойства следуют непосредственно из результатов предыдущего раздела (Свойство особенной корректности аргументировано в замечании 5). Поддельное доказательство может быть сгенерировано только при двух условиях.
1. Случайное число t является одним из особенных значений, для которых
2. Случайное число t не является одним из особенных значений из пункта 1, а протокол ПДПЛУ сфальсифицирован.
По следствию 2 вероятность события из пункта 1 не превосходит (k-1)/q и вероятность события из пункта 2 равна (q-k+1)/q2 исходя из результатов предыдущего раздела.
Улучшение сложности
Как размер, так и сложность протокола простого k-перетасовывания можно улучшить. Вместо использования следствия 2 будем использовать следствие 4. Интуитивно мы бы хотели заменить k копий D и k копий С в (16) на единственные числа соответственно. К сожалению, с такой заменой протокол потерял бы свойство нулевого разглашения. Вместо указанного, модифицируем протокол следующим образом.
Протокол простого k-перетасовывания II:
1. Р генерирует случайно и независимо элемент β из Zq и τ из Zq/{0}, вычисляет
и передает В и T проверяющему V.
2. V случайно генерирует элемент λ из Zq и передает λ, доказывающему Р.
3. Р вычисляет элемент s по формуле
и передает s проверяющему V.
4. V генерирует случайный элемент t из Zg и передает его доказывающему Р.
5. Р и V открыто вычисляют U=Dt=gdt, W=Сt=gct,
6. Р секретно случайно и равновероятно порождает k элементов из Zq:θ1,...,θk.
Затем Р вычисляет
и передает проверяющему V последовательность A1,...,Ak+1.
1. V генерирует случайный элемент γ ∈ Zq и передает его доказывающему Р.
8. Р вычисляет k элементов из Zq:r1,..., rk, удовлетворяющих соотношениям
и передает последовательность r1,...,rk проверяющему V.
9. V принимает доказательство тогда и только тогда, когда выполняются равенства (20).
Теорема 3. Протокол II доказательства для простого k-перетасовывания является пятиходовым, с открытой монетой доказательством знания соотношения в равенстве (15). Он удовлетворяет свойству особенной корректности и является протоколом с особенным нулевым разглашением при честном проверяющем. Число возведений в степень, необходимое для проведения доказательства, равно k+4 и число возведений в степень, необходимых для проверки доказательства, равно 2k+2.
Если V генерирует элементы t случайно, то вероятность фальсификации при доказательстве не превосходит
(k-1)/q+(q-k+1)/q2=(qk-q+q-k+1)/q2<k/q.
Набросок доказательства. Все рассуждения очень похожи, свойство за свойством, на рассуждения, приводимые в случае первоначального протокола. Основное отличие заключается в том, что ссылки на следствие 2 заменяются ссылками на следствие 4. Определение 6. Обозначим случай протокола II простого k-перетасовывания через
где и С и D задаются так же, как в определении 5.
Общее k-перетасовывание
Очевидным ограничением протокола простого k-перетасовывания является то, что доказывающий Р должен знать все показатели степени х1,...,xk и у1,...,yk. Во многих приложениях дело обстоит по-другому. Цель данного раздела заключается в устранении данного ограничения.
Задача общего k-перетасовывания:
Две последовательности Х1,..., Xk и Y1,...,Yk элементов из Zp известны. Дополнительно только доказывающему Р известны константы с и d, а элементы С=gс и D=gd сделаны известными всем. Доказывающему Р необходимо убедить V, что существует некоторая перестановка π ∈ Σk, обладающая свойством
для всех 1≤i≤k-1, при этом нельзя раскрывать никакой информации о π, с или d.
Протокол доказательства для общего k-перетасовывания.
Для удобства описания рассмотрим случай d=1. Общий случай может быть сведен к данному случаю простой заменой порождающего элемента группы с g на С и заменой с на c/d.
1. Для 1≤i≤k доказывающий Р генерирует случайно и независимо элементы ai, bi, ui и wi из Zq и вычисляет
Также Р генерирует γ из Zq/{0} и случайно и независимо друг от друга генерирует z0, z1 из Zq и вычисляет
и для 1≤i≤k
и, наконец,
затем Р передает упорядоченные последовательности Аi, Вi, Сi Ui и Wi вместе с Х0, Y0 и Λ проверяющему V.
2. Для 1≤i≤k проверяющий V случайно и независимо выбирает еi из Zq/{0} и передает последовательность доказывающему Р.
3. P вычисляет
для всех 1≤i≤k и передает вычисленные значения проверяющему V.
4. V генерирует случайный элемент t из Zq/{0} и передает его доказывающему Р.
5. Для 1≤i≤k доказывающий Р тайно вычисляет экспоненты
ri=ai+t ei bi (27)
si=γrπ(i).
6. Затем Р и V выполняют простое k-перетасовывание SSk(, g, Г), где
Заметим, что Р не нужно прямо вычислять Ri и Si, для построения доказательства, а V может вычислять Ri и Si так: Ri=Аi и Si=Сi Dt i.
Таким образом, при выполнении данного протокола доказательства доказывающий Р проводит k+4 возведений в степень, а V вычисляет 4k+2 экспоненты.
7. Р открывает значения
8. V проверяет, что
gσ i=WiSi/C,
и вычисляет
9. Р вычисляет
и выполняет вместе с V два доказательства Чаума-Педерсена CP(g, Г, G, G0) и CP(g, С, Z1, G0, G1). Таким образом, V убеждается в выполнении равенств 32.
10. Наконец V проверяет, что
11. V убеждается в правильности доказательства тогда и только тогда, когда
(а) Все проверяемые равенства верны (шаги 8 и 10),
(б) V принимает доказательство простого перетасовывания на шаге 6,
(в) V принимает оба доказательства Чаума-Педерсена на шаге 9.
Применение протоколов для голосования с несколькими уполномоченными
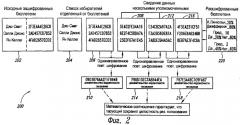
В работе [2] можно найти основное описание ситуации для применения протоколов при обыкновенном голосовании. Голоса представляются в виде пар схемы Эль-Гамаля в следующей форме: (или последовательности таких пар, если нужно больше данных), где m представляет собой некоторое стандартное шифрование ответов избирателей, αi секретно генерируются голосующими и h - это открытый параметр, который строится с помощью схемы разделения ключей без дилера ([7]). После закрытия избирательных участков (голосование закончено), независимые уполномоченные лица последовательно перетасовывают бюллетени. Каждое перетасовывание выполняется следующим образом:
где г, выбираются случайно из Zq и
(Xi,Yi)=(gαi,hαiMi).
После заключительного перетасовывания, окончательный набор зашифрованных бюллетеней расшифровывается в соответствии с пороговой схемой и открытые тексты ответов голосующих подсчитываются по обычным правилам проведения выборов.
Число уполномоченных лиц, принимающих участие в последовательном перемешивании, может быть произвольным и они могут быть совсем другими лицами, а не теми, кто обладает частями секретного ключа для голосования. Последовательность бюллетеней, которые, в конце концов, расшифровываются, можно только сравнить с исходной последовательностью представленных бюллетеней, если все перетасовывающие уполномоченные лица тайно сговорятся, так как каждая из их перестановок является совершенно произвольной.
Хотя форма каждого перетасовывания отличается от перетасовывания, обсуждавшегося в разделе 5, протокол доказательства можно построить с помощью лишь небольших изменений. Детали протокола будут представлены в следующим подразделе.
Перетасовывания пар схемы Эль-Гамаля
1. Для 1≤i≤k доказывающий Р генерирует случайно и независимо элементы аi, bi, ui и wi из Zq и вычисляет
также Р генерирует γ из Zq/{0} и случайно и независимо друг от друга генерирует x0, у0 и t0 из Zq и вычисляет
и для 1≤i≤k,
и, наконец,
затем Р передает упорядоченные последовательности Аi, Вi, Сi Ui и Wi вместе с Х0, Y0 и Λ проверяющему V.
1. Для 1≤i≤k проверяющий V случайно и независимо выбирает еi из Zq / {0} и передает данную последовательность Р.
3. Р вычисляет
для всех 1≤i≤k и передает вычисленные значения проверяющему V.
4. V генерирует элемент с из Zq/{0}и передает его доказывающему Р.
5. Для 1≤i≤k доказывающий Р тайно вычисляет
6. Затем Р и V выполняют простое k-перетасовывание SSk(, g, Г), где
Заметим, что P не нужно прямо вычислять Ri и Si для построения доказательства, а V может вычислять Ri и Si так: Ri=Ai Bi ce i и Si=Сi Di c.
Таким образом, при выполнении протокола доказательства, Р проводит k+4 возведений в степень, а V вычисляет 4k+2 экспоненты.)
7. Р открывает значения
8. V проверяет, что
и вычисляет
9. Р вычисляет
и выполняет вместе с V два доказательства Чаума-Педерсена CP(g, Г, G, G0) и CP(g, Г, H, H0). (Таким образом, V убеждается в выполнении равенств 45.)
10. Р и V вычисляют
11. Р вычисляет
и передает его проверяющему V.
12. Наконец V проверяет, что
13. V принимает доказательство тогда и только тогда, когда
(а) Все проверяемые равенства верны (шаги 8 и 12),
(б) V принимает доказательство простого перетасовывания на шаге 6,
(в) V принимает оба доказательства Чаума-Педерсена на шаге 9.
Однопроходное сведение результатов
При стандартной реализации предполагается, что данная операция содержит две различные фазы:
Перетасовывание (или перемешивание). Набор зашифрованных бюллетеней перемешивается. Это означает, что зашифрованная (и итерационно перетасованная) избирательная урна должна последовательно проходить от одного уполномоченного лица к другому до тех пор, пока не будет выполнено достаточное количество стадий перемешивания.
Более точно, пусть А1,..., An - последовательность перетасовывающих или перемешивающих субъектов, обычно называемых уполномоченными. Пусть В - это последовательность зашифрованных бюллетеней. Последовательно каждый Аi выполняет следующие операции.
1. Аi получает
B=((X1,Y1),...,(Xk,Yk))
от Ai-1, также он получает все н