Обнаружение фальсифицированных избирательных бюллетеней

Обнаружение фальсифицированных избирательных бюллетеней

Иллюстрации

Показать все

Реферат

Данное изобретение испрашивает приоритет временной заявки США №60/270182, поданной 20 февраля 2001, временной заявки США № (номер реестра патентного ведомства 32462-8006US02), поданной 11 февраля 2002, и является частичным продолжением заявки на патент США №09/534836, поданной 24 марта 2000; заявки на патент США №09/535927, поданной 24 марта 2000; и заявки на патент США №09/816869, поданной 24 марта 2001. Полное содержание этих пяти заявок включается в данное описание.

Область техники, к которой относится изобретение

Данное изобретение относится к области автоматизации выборов и используемых для этого криптографических технологий.

Уровень техники

Проблемы неточности и неэффективности давно сопровождают обычные, «выполняемые вручную» выборы. Хотя считается, что можно использовать компьютеры для проведения выборов более точно и эффективно, компьютеры приносят с собой собственные проблемы. Поскольку электронные данные можно так легко изменять, то многие электронные системы выборов склонны к многочисленным ошибкам, появление которых намного менее вероятно в обычных системах проведения выборов.

Один класс таких ошибок основывается на неопределенной целостности компьютера голосующего избирателя или других вычислительных устройств. В современных условиях использования компьютеров в сетях чрезвычайно трудно содержать любую машину защищенной от злонамеренного программного обеспечения. Такое программное обеспечение часто способно оставаться скрытым в компьютере в течение длительных периодов времени, прежде чем оно действительно выполнит наносящее вред действие. В то же время оно может тиражироваться в другие компьютеры в сети или в компьютеры, которые имеют минимальное взаимодействие с сетью. Оно может даже передаваться в компьютеры, которые не включены в сеть, за счет постоянного использования пользователями носителей информации.

В контексте электронных тайных выборов с избирательными бюллетенями этот вид злонамеренного программного обеспечения является особенно опасным, поскольку даже когда его вредное действие запускается, оно может оставаться незамеченным, и поэтому способно срывать выборы в последующем. Управляемые тесты логики и точности (тесты ЛТ) следят за обработкой испытательных избирательных бюллетеней для определения, работает ли правильно система голосования, и их можно использовать в качестве попытки обнаружения злонамеренного программного обеспечения, присутствующего в компьютере избирателя. Однако тесты ЛТ чрезвычайно трудно выполнять правильно, поскольку возможно, что вредное программное обеспечение способно различать действительные и испытательные избирательные бюллетени и может не влиять на все испытательные избирательные бюллетени. Поскольку требование тайны выборов исключает возможность проверки действительных избирательных бюллетеней на предмет фальсификации, то могут оказаться бесполезными даже тщательные тесты ЛТ. Проблема борьбы с этой угрозой известна как проблема доверия к исполнителю.

Большинство существующих способов решения этой проблемы доверия к исполнителю фокусировалось на способах защиты платформы голосования и создания тем самым определенности, что компьютер избирателя является «чистым» или «не зараженным». К сожалению, затраты на экспертизу и выполнение рутинных операций, которые необходимы для обеспечения приемлемого уровня такой определенности, требуют установки электронных избирательных систем в управляемые условия узла подсчета голосов, где исполнительные системы компьютеров можно поддерживать и контролировать с помощью экспертов по компьютерам и сетям. Эти системы узлов подсчета голосов могут обеспечивать некоторые преимущества за счет упрощения конфигурации, простоты использования, эффективности сведения результатов в таблицы и стоимости. Однако этот подход не обеспечивает использования большого потенциала распределенной связи, которая используется в мировой электронной торговле.

В соответствии с этим решение проблемы доверия к исполнителю, которое не требует защиты избирательной платформы от злонамеренного программного обеспечения и которое обеспечивает использование практически любой компьютерной системы в любом месте в качестве избирательной платформы, может иметь большую важность.

Краткое описание чертежей

На чертежах изображено:

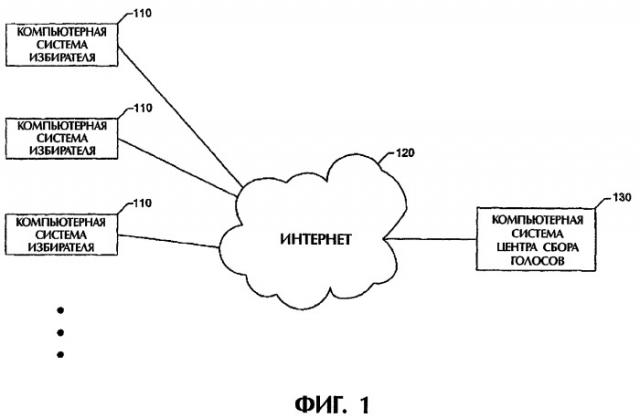
фиг.1 - укрупненная блок-схема типичных условий, в которых работает средство;

фиг.2 - блок-схема некоторых компонентов, обычно содержащихся по меньшей мере в некоторых компьютерных системах и других устройствах, на которые воздействует средство;

фиг.3 - графическая схема стадий, обычно выполняемых средством для обнаружения фальсифицированного избирательного бюллетеня.

Описание наилучших вариантов осуществления изобретения

Создано средство обнаружения избирательных бюллетеней, фальсифицированных злонамеренными программами («средство обнаружения»). Подход, используемый средством обнаружения, обычно не содержит попыток исключения или предупреждения появления злонамеренного программного обеспечения в компьютере для голосования. Вместо этого оно предлагает криптографически защищенный для избирателя способ верификации избирательного бюллетеня в том виде, в котором он принят в центре сбора голосов, без раскрытия информации о содержимом (выборе кандидатов) для самого центра сбора голосов. То есть центр сбора голосов может точно подтвердить избирателю, какой выбор кандидатов принят, не зная, каким является выбор. Таким образом, избиратель может обнаружить любую разницу между выбором избирателя и действительным выбором, принятым в центре сбора голосов (как представлено в передаваемых цифровых данных избирательного бюллетеня). Кроме того, при каждых выборах можно выбирать из гибкого набора стратегий принятия решений, позволяющих избирателю повторно опустить избирательный бюллетень в случае, когда принятый выбор отличается от задуманного выбора.

Ниже приводится описание средства обнаружения в контексте довольно стандартных условий выборов. Для простоты представления в начальном описании средства обнаружения предполагается, что избирательный бюллетень содержит только один вопрос и что имеется набор из К разрешенных ответов a₁,..., a_k (один из которых может быть «воздержался»). Для специалистов в данной области техники понятно, что целесообразно обобщить ответ, возможный в этой ситуации, для обработки огромного большинства действительных конфигураций избирательных бюллетеней в мире.

Некоторые типичные криптографические признаки избирательных установочных параметров заключаются в следующем:

1. Состав избирательного бюллетеня: набор криптографических параметров выборов заранее согласовывается администрацией выборов и широко оглашается с помощью публикации или других таких средств. Важными параметрами являются шифровальная группа, генератор, открытый ключ выборов и схема кодирования решений. А именно таковыми являются:

(а) Шифровальная группа, G может быть Z_p, где р является большой первичной группой или группой эллиптической кривой.

(b) Генератор, g∈G. В случае G=Z_p, g должно генерировать подгруппу <g> из G*, которая имеет большой первичный порядок q. В случае эллиптической кривой предполагается, что <g>=G и q=p.

(c) Открытый ключ выборов, h∈(g).

(d) Схема кодирования решения: разделение <g> на «назвать представителей». То есть <g>=S₀∪S₁∪...S_K, где S_к являются парными несвязанными подмножествами <g>. Для каждого 1≤k≤K любое сообщение m∈S_k представляет голосование за a_k. Остальные сообщения рассматриваются как недействительные. Обычно каждое S_k при 1≤k≤K состоит из одного элемента μ_k, хотя это в принципе не является обязательным. Однако для защиты схемы в целом необходимо, чтобы μ_k генерировались независимо или случайно с использованием некоторого открытого случайного источника или с помощью приемлемой схемы совместного пользования.

Хотя в последующем описании используется система обозначения мультипликативных групп для единообразия, понятно, что можно также хорошо осуществлять все построения с использованием эллиптических кривых.

2. Представление голосования: каждый избиратель ν_i шифрует свой выбор или решение в виде пары ЭльГамаля (X_i,Y_i)=(g^αi,h^αi,m_i), где α_i∈Z_q выбирается произвольно избирателем, и m_i∈S_k, если ν_i; желает выбрать ответ а_k. Эта зашифрованная величина затем передается в центр сбора голосов, обычно с присоединением цифровой подписи, созданной избирателем ν_i.

Если избиратель ν_i вычислял бы эти величины сам, например, с помощью карандаша и бумаги, то этот протокол был бы по существу достаточным для осуществления тайного голосования, универсально проверяемой системы выборов. (В зависимости от способа табуляции была бы необходима некоторая дополнительная информация, такая как подтверждение личности избирателя.) Однако, поскольку на практике избиратель ν_i выполняет лишь выбор с помощью какого-либо интерфейса пользователя, то не имеет смысла ожидать, что он будет следить за действительной величиной переданных битов и будет проверять их на предмет соответствия своему задуманному выбору. Короче говоря, исполнитель голосования может игнорировать замысел и передавать «выбираю μ_j», когда избиратель в действительности хотел передать «выбираю μ_k».

Обычно избирателю необходимо иметь какой-то путь для проверки того, что зашифрованный выбор, который был принят в центре сбора голосов, совпадает с его собственным выбором. Попросту сделать данные избирательного ящика открытыми не было бы разумным решением, поскольку исполнитель голосования, а не избиратель выбирает α_i. С целью обеспечения тайны выборов и приведения типа данных эта величина должна быть «потеряна». Таким образом, зашифрованный выбор избирателя ν_i является непрозрачным как для него самого, так и для любого другого. Обобщенное подтверждение из центра сбора голосов очевидно также не является достаточным. Основными необходимыми свойствами являются свойства:

1. Подтверждающая цепочка С, возвращаемая центром сбора голосов, должна быть функцией принятых данных (зашифрованного выбора).

2. Избиратель и исполнитель голосования должны быть в состоянии выполнять специальный набор стадий, которые позволяют избирателю привязать С исключительно к выбору (или голосу) μ_k, который был принят.

3. Для исполнителя голосования должно быть невозможным вести себя так, что избиратель является обманутым. То есть исполнитель не должен убеждать избирателя, что было принято μ_k, если в действительности было принято μ≠μ_k.

В следующем разделе приведено описание такой схемы, которая будет называться SVC, в ее основной форме. В следующих разделах будут описаны некоторые улучшения и дополнения.

В качестве части процесса голосования обычно выполняются следующие стадии.

СС-1. Исполнитель голосования М_i, приводимый в действие избирателем ν_i, создает зашифрованный избирательный бюллетень от имени избирателя ν_i, как и прежде. Обозначим это как (X_i,Y_i)=(g^αi,h^αi,m_i) для некоторой величины m_i∈〈g〉 и α_i∈Z_q.

СС-2. M_i должен также создать доказательство достоверности Р_i, которое является доказательством с нулевым знанием, что m_i∈{μ₁,...,μ_k} (такое доказательство легко создать из основного доказательства Чаум-Педерсона для равенства дискретных логарифмов с использованием технологии, указанной в [CDS94]. Специальный пример можно найти в [CGS97]).

СС-3. Затем М_i передает как Р_i, так и (подписанный) выбор (X_i,Y_i) в центр сбора голосов.

СС-4. Перед признанием зашифрованного избирательного бюллетеня центр сбора голосов сначала проверяет доказательство Р_i. Если верификация Р_i потерпит неудачу, то искажение уже обнаружено, и центр сбора голосов может либо не выдать цепочку подтверждения или выдать некоторую случайную цепочку по умолчанию.

Сс-5. Если верификация Р_i прошла удачно, то центр сбора голосов вычисляет величины W_i и U_i в виде

,

где K_i∈G и β_i∈Z_q обычно генерируются произвольно и независимо (от избирателя к избирателю).

СС-6. Затем центр сбора голосов возвращает (W_i,U_i) к М_i.

СС-7. Исполнитель М_i вычисляет

и отображает эту цепочку (или более вероятно ее хеш-функцию Н(С_i)) для избирателя ν_i.

Избиратель должен знать, какую следует искать цепочку подтверждения. Это можно выполнять двумя разными путями. Наиболее прямым путем является получение избирателем ν_i величин К_i и β_i из центра сбора голосов. Это осуществимо, требует передачи очень небольшого количества данных и может подходить для некоторых случаев осуществления. Однако в других ситуациях это может быть непривлекательным подходом, поскольку в этом случае необходимо вычислять С_i или (Н(С_i)). Поскольку запрос исполнителя М_i на выполнение этих вычислений разрушает защиту схемы, то избиратель ν_i должен иметь доступ к дополнительным вычислительным устройствам, а также доступ к независимому каналу связи.

В качестве альтернативного решения центр сбора голосов вычисляет все возможные цепочки подтверждения для ν_i и передает результаты в словарь подтверждений избирателя ν_i через независимый канал. Обычно словарь подтверждений избирателя ν_i будет состоять из следующей таблицы в любом разумном формате:

Ответ	Цепочка подтверждения
α1	Н(Сi1)
α2	H(Ci2)
··	··
αк	H(CiK)

где Н является открытой (опубликованной) хеш-функцией выборов (возможно, функцией идентичности) и С_ij=К_iμ_j ^βi.

Естественно, что необходимо ответственно подходить к созданию независимого канала для обеспечения его действительной независимости. Однако для этого имеются решения. Поскольку К_i и βⁱ можно генерировать заранее перед выборами, то даже медленные способы доставки, такие как наземная почта, можно использовать для передачи словаря.

Для более полного описания средства обнаружения ниже приводится пример, иллюстрирующий работу некоторых вариантов его выполнения. Ниже приводится подробное описание примера закрытого обмена для подтверждения величины.

Для большей ясности примера несколько используемых основных параметров, например, число вопросов в избирательном бюллетене, и размер криптографических параметров намного меньше, чем обычно используются на практике. Кроме того, хотя аспекты примера обмена описывается ниже в конкретном порядке, для специалистов в данной области техники понятно, что их можно выполнять в различных других последовательностях.

Некоторые протоколы электронных выборов содержат дополнительные признаки, такие как:

- Информация сертификации избирателя и администрации (открытый ключ) для аутентификации и контроля;

- Параметры стиля страницы избирательного бюллетеня;

- Стандарты кодирования данных;

- Протокол и параметры табуляции.

Поскольку эти признаки являются независимыми от осуществления закрытого подтверждения величин, то их подробное описание не включено в данный пример.

В этом примере предполагается, что электронный протокол, который кодирует ответы избирателя, является единичной парой ЭльГамаля. Однако на основе последующего описания можно легко составить обмен закрытого подтверждения величин для других протоколов выборов с использованием шифрования ЭльГамаля для избирательных бюллетеней. Например, некоторые варианты выполнения средства включают гомоморфный протокол выборов, описанный в заявке на патент США №09/535927. В этом протоколе ответ избирателя представлен несколькими парами ЭльГамаля. Словарь подтверждений, используемый в этом примере, легко модифицировать для отображения сочленения соответствующих цепочек подтверждения или для отображения хеш-функции их последовательности.

Сначала должна быть согласована правовая основа данных инициализации выборов. Это включает по меньшей мере: основные криптографические числовые параметры, избирательный бюллетень (т.е. набор вопросов и разрешенных ответов и т.д.) и схема кодирования решений (это может также включать дополнительные данные, относящиеся к конкретно используемому протоколу выборов).

Криптографические параметры

- арифметика групп: целочисленная мультипликативная модульная арифметика;

первичный модуль: р = 47;

- модуль подгруппы: q = 23;

- генератор: g = 2;

- открытый ключ: h = gs, где s является закрытым. Для данного примера принимается, что h = gl2 = 7.

Избирательный бюллетень

- один вопрос

- текст 1 вопроса: Каким должен быть цвет нашего флага (можно выбрать максимально 1 цвет);

- число ответов/выбора: 4

* текст 1 ответа: синий

* текст 2 ответа: зеленый

* текст 3 ответа: красный

* текст 4 ответа: я воздерживаюсь.

Схема кодирования решений

Выбор	Величина ответа
Синий	9(μ1)
Зеленый	21(μ2)
Красный	36(μ3)
Я воздерживаюсь	17(μ4)

В некоторый момент времени перед выдачей подтверждения и перед распределением словарей подтверждения центр сбора голосов (или агентство) генерирует для каждого избирателя V_i случайные, независимые β_i и К_i. Если словарь подтверждений должен рассылаться после приема голоса, то эти параметры можно генерировать для каждого избирателя сразу после признания каждого проголосованного избирательного бюллетеня. В качестве альтернативного решения их можно генерировать заранее перед выборами. В данном примере агентство по сбору избирательных бюллетеней имеет доступ к этим параметрам как непосредственно после признания проголосованного избирательного бюллетеня, так и непосредственно перед передачей соответствующему избирателю словаря подтверждений.

В некоторый момент времени в течение официального времени выборов каждый избиратель V получает и аутентифицирует данные инициализации выборов, указанные выше. Их можно получить, направив запрос на избирательный бюллетень в любой избирательный сервер. В качестве альтернативного решения законодательные органы могут иметь подходящие средства для публикации данных инициализации выборов, т.е. сделать их удобным образом доступными для всех избирателей.

Из данных инициализации выборов избиратель V способен определить, что ожидаемый ответ является стандартным кодированием конкретной последовательности из двух различимых элементов данных. Ими являются (в их точном порядке):

Шифрование выбора

Пара целых чисел (X,Z), где 0≤X,Z<47, указывающих (в зашифрованном виде) выбор, или ответ, избирателя. Например, для того чтобы ответ был действительным, он должен быть дан в виде (X,Y)=(2^α,7^α _μ), где 0≤α<23 и μ∈{9,21,36,17}.

Доказательство достоверности

Доказательство достоверности должно показывать, что (X,Y) имеет вид, описанный на стадии шифрования выбора (в данном примере, необходимо видеть, что это доказательство состоит из 15 модульных целых чисел, расположенных в специальной последовательности).

В данном примере предполагается, что избиратель V желает отдать голос за «зеленый».

1. Избиратель генерирует по случайному закону α∈Z₂₃. В данном примере α = 5. Поскольку кодированием «зеленого» является 21, то выбор избирателя V вычисляется как

Эта пара является тем, что должно быть передано в центр сбора голосов.

Возможной опасностью является то, что компьютер избирателя V может попытаться изменить эти величины.

Избиратель V (или точнее компьютер избирателя V) должен доказать, что соблюдается одно из следующих условий

1. (X,Y)=(2^α,7^αx9), то есть выбор (отданный голос) означает «синий»;

2. (X,Y)=(2^α,7^αx21), то есть выбор (отданный голос) означает «зеленый»;

3. (X,Y)=(2^α,7^αlx36), то есть выбор (отданный голос) означает «красный»;

4. (X,Y)=(2^α,7^αx21), то есть выбор (отданный голос) означает «я воздерживаюсь»

для некоторой неуказанной величины α без раскрытия ее действительного значения.

Для осуществления этого имеется множество стандартных способов. Смотри, например, R. Cramer, I. Damgard, В. Schoenmakers «Доказательства частичного знания и упрощенная конструкция протоколов сокрытия свидетеля», Advances in Criptology - CRYPTO'94, Lecture Notes in Computer Science, страницы 174-187, издательство Springer-Verlag, Берлин, 1994. Технология закрытого подтверждения величин, используемая средством, работает также хорошо с любым способом, который соответствует абстрактным критериям предыдущего параграфа. Хотя ниже приведены детали одного такого способа доказательства достоверности, в вариантах выполнения средства можно использовать доказательства достоверности другого типа.

Состав доказательства достоверности

(В последующем каждое действие или вычисление, которое должен выполнять избиратель V, в действительности выполняется компьютером избирателя V).

1. V устанавливает α2=α=5.

2. V генерирует ω₂∈_RZ₂₃,r₁,r₃,r₄∈_RZ₂₃,S₁,S₃,S₄∈_RZ₂₃, все по случайному закону и независимо. Для данного примера принимается

3. V вычисляет соответствующие величины

4. V использует опубликованную хеш-функцию для вычисления c∈Z₂₃ как

Поскольку можно выбирать различные хеш-функции, то для данного примера выбирается любая случайная величина, например,

(На практике для вычисления Н можно использовать SHA1 или MD5 или другие стандарты, защищающие хеш-функцию).

5. V вычисляет интерполяционный многочлен Р(х) степени 4-1=3.

Заданными свойствами Р являются

P(x)=Σ³ _j=0 Z_j X_j вычисляется с использованием стандартной теории многочленной интерполяции с получением:

или

6. V вычисляет величины

r₂=ω₂+α₂s₂=4+5х5=6

7. Доказательство достоверности V состоит из 12 чисел

и трех чисел

в точной последовательности (z₀ можно не передавать, поскольку она вычисляется из других элементов данных, передаваемых с использованием опубликованной хеш-функции Н).

После вычисления необходимого зашифрованного выбора (X,Y) и соответствующего доказательства достоверности, избиратель V кодирует эти элементы в последовательности, заданной стандартным форматом кодирования. Полученные последовательности образуют проголосованный избирательный бюллетень избирателя V. (Для того чтобы сделать проголосованный избирательный бюллетень неизменяемым и неоспоримым, избиратель V может также подписать в цифровом виде этот проголосованный избирательный бюллетень с помощью своего личного ключа подписи). Полученная комбинация из проголосованного избирательного бюллетеня и подпись избирателя V (точнее, стандартное кодирование этих двух элементов) образуют его подписанный проголосованный избирательный бюллетень). Наконец, каждый избиратель передает свой (не обязательно, подписанный) проголосованный избирательный бюллетень обратно в центр сбора голосов.

Как указывалось выше, специфичные случайные параметры для избирателя V (β и К) являются доступными в центре сбора голосов. В данном примере это

После получения проголосованного избирательного бюллетеня избирателя (не обязательно подписанного) в центре сбора голосов выполняются следующие стадии:

1. Проверяется цифровая подпись для определения аутентичности избирательного бюллетеня, а также права избирателя на участие в выборах.

2. Если проверка подписи на стадии 1 верифицирована как правильная, то центр сбора голосов проверяет затем доказательство достоверности. Для частного типа доказательства достоверности, который выбран для использования в данном примере, это состоит в следующем:

(a) Используется хеш-функция Н для вычисления величины

P(0)=z₀

(Напоминаем, что остальные коэффициенты Р, z₁, z₂, z₃ являются частью переданного проголосованного (не обязательно подписанного) избирательного бюллетеня избирателя V).

(b) Для каждого 1≤j≤4 оцениваются обе стороны уравнений

(В данном случае, как указывалось выше, μ_j берется из схемы кодирования решений). Если уравнение не сходится в любом из случаев, то верификация не состоится. Этот избирательный бюллетень не признается, и к избирателю V обратно передается произвольная цепочка (указатель) отказа.

3. При успешно выполненной предыдущей стадии ответная цепочка (W, U) вычисляется как

Эта последовательная пара кодируется, как задано форматом открытого кодирования, и возвращается избирателю V.

4. Система избирателя V вычисляет

и отображает эту цепочку избирателю (в качестве альтернативного решения протокол может определять, что открытую хеш-функцию следует вычислять из С. В данном примере отображается сама С). Если компьютер избирателя V попытается передать выбор, отличающийся от «зеленого», то вычисленная выше величина С будет другой. Более того, правильная величина С не может быть вычислена из неправильной величины без решения проблемы Диффи-Хеллмана (для небольших величин р и q, которые выбраны в данном примере, это возможно. Однако для реальных криптографических параметров, компьютер избирателя V не способен выполнить это). Таким образом, если компьютер избирателя V передал зашифрованный избирательный бюллетень, который не соответствует выбору избирателя V, то имеются лишь две возможности в тот момент времени, когда от него ожидается отображение подтверждения. Он может отобразить что-нибудь, или же он может ничего не отобразить. В случае, когда не отображается ничего, то избиратель V может воспринимать это как указание на то, что избирательный бюллетень фальсифицирован. В случае, когда отображается что-нибудь, то это наверное будет неправильным, и избиратель V снова может сделать вывод, что избирательный бюллетень был сфальсифицирован.

Затем избиратель V сравнивает величину С, отображенную на дисплее, с величиной, находящейся в словаре подтверждений избирателя V, соответствующей выбору «зеленый» (задуманный избирателем V выбор). В это время избиратель V мог уже получить заранее свой словарь подтверждений, или же мог получить его копию через любой независимый канал. Примером такого канала может быть использование факса. Если отображенная величина не совпадает с соответствующей цепочкой подтверждения в словаре подтверждений, то фальсификация обнаружена, и избирательный бюллетень можно «опустить» повторно в соответствии с выбранной для выборов стратегией.

Словарь подтверждений для каждого избирателя вычисляет центр сбора голосов, поскольку, как указывалось выше, он является органом, который располагает знанием специфичной для избирателя величины α и К. В случае рассматриваемого избирателя V словарь вычисляется в виде

Выбор	Цепочка подтверждения
Синий	Cl=Kμ1 β=37x918=16
Зеленый	C2=Kμ2 β=37х2118=18
Красный	C3=Kμ3 β=37х3618=36
Я воздерживаюсь	C4=Kμ4 β=37xl718=8

Описание уровня защиты, обеспечиваемого средством при использовании схемы закрытого подтверждения величин, приводится ниже: предположим, что А является противником исполнителя голосования, и ∈₀ является верхним пределом вероятности того, что А способен подделать доказательство достоверности для любого заданного μ_i,...,μ_k (мы знаем, что ∈₀ является пренебрежительно малым).

Теорема 1. Предположим, что схема закрытого подтверждения величин выполняется с Н=Id. При этом 1≤k₁≠k₂≤K. Предположим, что для некоторого ∈>0 можно с вероятностью ∈ передать b_i=(g^αih^αiμ_k1) и отобразить С_ik2=K_iμ_k2 ^βi, где вероятность принята равномерной по всей комбинации величин для μ₁,...,μ_kg,h,β_i и К_i. Тогда А может решить случайный пример а проблемы Диффи-Хеллмана с вероятность ∈ и дополнительной работой О(К).

Доказательство. Предположим, что А имеет X,Y,Z∈_R<g>. А может имитировать выборы и обмен закрытого подтверждения величин посредством выбора независимо по случайному закону C_ik1<g> и μ_k∈〈g〉 для всех устанавливая h=X,h^βi=Y и μ_k2=μ_k1Z. Полученное распределение параметров выборов и C_ik1 очевидно является идентичными с распределением, которое получается в результате действительных выборов. С вероятностью ∈ противник А может отобразить С_ik2 и может тем самым вычислить

Таким образом, log_xC=β_ilog_xYlog_xZ и С является решением примера проблемы Диффи-Хеллмана, представленного тройной величиной (X,Y,Z).

Следствие 1. Предположим снова, что схема закрытого подтверждения величин выполняется с Н=Id. При этом 1≤k₁≠k₂≤K. Предположим, что для некоторого ∈₁>0 противник А может с вероятностью ∈₁ выбрать k₁≠k₂, передать b_i=(g^αih^αiμ_k1) и отобразить C_ik2=K_iμ_k2 ^βi, где вероятность принята равномерной по всей комбинации величин для μ₁,...,μ_K,g,h,β_i и К_i. Тогда А может решить случайный пример а проблемы Диффи-Хеллмана с вероятность ∈₁/(K-l) и дополнительной работой 0(К).

Доказательство: необходимо следовать доказательству теоремы 1, но относительно проблемы нахождения решения для по меньшей мере одной проблемы К-1 Диффи-Хеллмана.

Следствие 2. Предположим, что является верхней границей вероятности того, что А может решить случайный пример проблемы Диффи-Хеллмана. Тогда в случае H=Id верхней границей вероятности того, что А может передать выбор а, который отличается от выбора избирателя, и тем не менее отобразить правильную цепочку подтверждения, является ∈₀+(K-l)∈_DH.

Если хеш-функция Н является не тривиальной, то нельзя надеяться на сравнение возможности решения проблемы Диффи-Хеллмана без значительного специального знания свойств Н. Вместо того чтобы оценивать защиту схемы для специально выбранных Н, предположим лишь, что Н имеет пренебрежительно малую вероятность совпадения, и вместо этого оценим защищенность проблемы Диффи-Хеллмана для принятия решений. Вариантом этой проблемы может служить следующее. А имеет последовательность набора чисел (X_n,Y_n,Z_n,C_n), где X_n,Y_n,Z_n генерированы независимо по случайному закону. С вероятностью 1/2 С_n является решением примера (X_n,Y_n,Z_n) проблемы Диффи-Хеллмана, и с вероятностью 1-1/2=1/2 С_n генерирована по случайному закону и независимо. Говорится, что А имеет преимущество ∈-DDH, если А может с вероятностью 1/2+е получить ответ на вопрос logx_nC_n=logx_nZ_nlogx_nZ_n?

Теорема 1 и следствия 1 и 2 очевидно имеют аналоги в случае H≠Id (только при предположении, что Р имеет пренебрежительно малую вероятность совпадения). Оба утверждения и доказательства выполняются с небольшими вариациями, поэтому можно подвести итог следующим образом:

Следствие 3. Предположим, что является верхней границей преимущества DDH противника А. Тогда, если Н является любой хеш-функцией с пренебрежительно малой вероятностью совпадения, то верхней границей вероятности того, что А может передать выбор а, который отличается от выбора избирателя, и тем не менее отобразить правильную цепочку подтверждения, является ∈₀+(К-1)∈_DDH.

Схема закрытого подтверждения величин не может обеспечить какой-либо защиты, если противник А контролирует также центр сбора голосов. Если это так, то А имеет доступ к К_i и β_i и таким образом может легко отображать любую правильную цепочку подтверждения по своему выбору. Это представляется маловероятным, поскольку центр сбора голосов будет неопровержимо изобличен в случае раскрытия таких действий. Тем не менее, в случае, когда недопустимо доверять центру сбора голосов в этом отношении, ответственность за подтверждение можно распределять между многими выбранными администрациями.

Для распределения ответственности за подтверждение каждая администрация A_j при 1≤j≤J, генерирует (для избирателя ν_i) независимо и по случайному закону К_ij и β_ij. Администрации могут их комбинировать двумя общими способами.

1. Конкатенация. Цепочка подтверждения для избирателя вычисляется в виде конкатенации в заданном порядке отдельных цепочек подтверждения (вычисляемых по отдельности, как и в предшествующей части), соответствующих каждой администрации J. В этом случае подтверждение является успешным, только если все субцепочки будут верифицированы как правильные.

2. Достоверный сервер или принтер. Если допустимо доверять единственному центральному серверу или принтеру, то множество цепочек подтверждения можно объединять в одну цепочку того же размера с помощью простого вычисления

Это дает преимущество уменьшения количества данных подтверждения, которые необходимо передавать избирателю, однако за счет создания центральной точки для атаки на систему.

Всегда желательно сократить размер данных, которые необходимо передавать избирателю через независимый канал. Как было описано в части 3, словарь подтверждений уже является небольшим по стандартам современной технологии связи, однако может быть предпочтительным с точки зрения стоимости передавать еще меньше данных. Как указывалось выше, один подход может заключаться в передаче закрытых К_i и β_i непосредственно избирателю, однако это имеет тот недостаток, что на избирателя перекладывается слишком большая вычислительная нагрузка, которую он не может выполнить в уме или на бумаге. Следующая вариация схемы закрытого подтверждения величин обеспечивает достижение обеих целей - меньше данных для передачи через независимый канал связи и меньше устного счета для избирателя. Это осуществляется за счет того, что повышается вероятность обмана избирателя противником, однако это может быть приемлемым с точки зрения всех выборов. Даже если вероятн