Способ измерений горизонтальных неровностей (рихтовки) и кривизны в плане рельсовых нитей

Способ измерений горизонтальных неровностей (рихтовки) и кривизны в плане рельсовых нитей

Иллюстрации

Показать все

Реферат

Способ может быть использован для контроля и прогноза состояния железнодорожного пути и заключается в том, что измеряют при помощи инерциальной навигационной системы (ИНС), расположенной над шкворнем измерительной тележки, текущий курс путеизмерительного вагона и при помощи датчика угловых перемещений текущий угол виляния измерительной тележки относительно кузова, а также при помощи датчиков букса-рельс измеряют расстояния от реборд соответствующих колес тележки до головок рельсов. По полученной информации рассчитывают текущие курсы рельсовых нитей. Значения горизонтальных неровностей рельсовых нитей получают как произведение базы тележки на отклонения текущих курсов рельсовых нитей от текущих усредненных на базе тележки курсов рельсовых нитей. Текущие радиусы кривизны рельсовых нитей получают делением базы тележки на приращения курсовых углов рельсовых нитей на базе тележки.

Изобретение относится к контролю состояния железнодорожного пути.

Известен способ измерения стрелы изгиба в плане (рихтовки) от несимметричной хорды, при котором измеряют по каждой рельсовой нити сумму горизонтальных перемещений рельса в трех точках (через 4,5 м и 17 м) относительно кузова вагона с помощью оптических датчиков кузов-рельс [1].

Известен способ измерения кривизны пути в плане [1], которая определяется по изменению угла поворота скользящей вдоль пути хорды длиной, равной базе вагона в горизонтальной плоскости. Угол поворота равен курсовому углу (азимуту продольной оси кузова), измеряемого ИНС, минус угол виляния кузова, определяемый по разности горизонтальных перемещений противоположных концов кузова относительно рельсовой нити, измеряемых оптическими датчиками рельс-кузов.

Горизонтальные неровности рельсовых нитей полностью характеризуются рихтовкой и кривизной пути в плане. Рихтовка рельсовых нитей это короткие неровности рельсовых нитей, определяемых как отклонения текущих положений рельсовых нитей от средних (аппроксимирующих) кривых.

Недостатками приведенных способов являются: искажение хордовым методом коротких горизонтальных неровностей (рихтовки); низкая точность измерения кривизны коротких кривых, например стрелочных переводов, обусловленная тем, что длина хорды сравнима с длиной кривой.

Рассмотрим более детально свойства хордовых способов измерения.

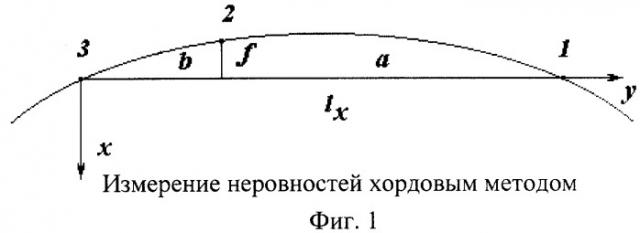
Предположим, что хорда длиной l_x=a+b скользит своими концами по кривой х(y) (см. фиг.1). Небольшая величина неровностей по сравнению с длиной хорды позволяет представить движение хорды как сумму вращения вокруг мгновенного центра на малые углы и поступательного перемещения этого центра со скоростью γ в направлении y. Выходной величиной хордового измерителя является длина f(y) стрелы изгиба, отстоящей на расстоянии b от конца хорды (точка 3 на фиг.1). Входным воздействием - неровность рельса х(y), которую представим в виде гармонической функции х=x₀cosωt.

Известно, что ординаты x_i точек 1, 2 и 3 кривой связаны с длиной стрелы ее изгиба соотношением

где

Выражение (1) позволяет получить передаточную функцию хордового метода. При воздействии гармонической неровности, имеющей частоту ω и амплитуду x₀, с учетом запаздывания, пропорционального постоянной скорости движения вагона ν, ординаты x_i(i=1,2,3) изменяются по закону

С учетом (1) и (2) длина стрелы изгиба при этом может быть представлена в виде

где

Таким образом, используя выражение (3), можно хордовому измерительному устройству сопоставить частотную передаточную функцию

W(iω=r(ω)e^-iϕ(ω).

Поскольку неровности удобнее представлять как функцию продольной координаты пути у, перейдем к новой независимой переменной, используя очевидное соотношение y=νt. Тогда гармоническая неровность принимает вид

где λ - длина волны неровности. Заметим, что правая часть выражения (5) не зависит от скорости движения вагона.

Если входным сигналом будем считать перемещение х₂ измерительного ролика или измеренное неконтактным датчиком расстояние от хорды до рельса, передаточная функция хордового измерительного устройства будет

где - "пространственная частота неровности".

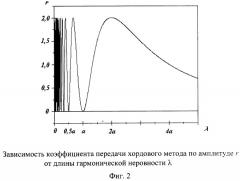
График зависимости модуля частотной передаточной функции r(λ), построенный в соответствии с выражением (4) для случая равноплечей хорды (а=b, l_х=2а), приведен на фиг.2. Из графика видно, что хордовый метод позволяет приблизительно восстановить форму неровности только при условии, что ее длина превышает длину хорды λ>а. При увеличении длины неровности чувствительность метода заметно падает.

Предложение использовать не только угловую, но и скоростную информацию, вырабатываемую ИНС, было сделано профессором С.П.Дмитриевым. Получен алгоритм определения горизонтальной и вертикальной неровностей с использованием углов курса и наклона вагона в продольной плоскости (тангажа) и скорости движения вагона. Однако, как справедливо отмечает сам автор, "угломерные методы определения профиля" характеризуются методической погрешностью, связанной с несовпадением касательной к линии пути и продольной оси вагона, являющейся, по существу, хордой длиной 20 м". Действительно, предложенный способ будет пропускать неровности, имеющие длину, равную длине хорды, поскольку при этом не происходит изменений угловой ориентации кузова вагона, а также будет иметь все недостатки, присущие хордовому методу.

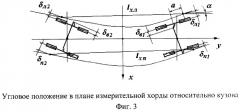
Рассмотрим эту ситуацию несколько подробнее применительно к контролю неровностей в горизонтальной плоскости. Для перехода от углового положения вагона к неровностям рельсов используются датчики поступательных перемещений фиксированных точек кузова относительно рельсов. Соединив контрольные точки на рельсе между собой, получим линию, которую условимся называть измерительной хордой (фиг.3). Угловое отклонение и параллельное смещение измерительной хорды от продольной оси кузова вагона оу может быть вызвано следующими причинами.

1. Смещением тележки от оси колеи в процесс поперечных колебаний или изменением ширины колеи. Это приводит к изменению расстояний δ_ij между буксой и рельсом (i=1, 2 - номер измерительной колесной пары; j=л, п - индекс левого и правого колес). Расстояния δ_ij измеряются неконтактными датчиками перемещений оптического или другого типа.

2. Поворотом тележек вокруг шкворня относительно кузова на углы α₁ и α₂. В результате расстояния между буксами первой и второй тележек и кузовом изменяется на величины

где а - расстояние от оси колеса до поперечной оси тележки. Выражение (7) справедливо для измерительной хорды l_х=l+2f, где l - расстояние между шкворнями первой и второй тележек.

3. Вилянием (рысканием) кузова вагона на рессорной подвеске относительно букс колесных пар. Если считать, что колебания вагона по углу рыскания происходят вокруг его центра масс, то δ_в1=-δ_в2.

Таким образом, суммарное угловое отклонение измерительной хорды от продольной оси вагона составит

Угловое положение измерительной хорды относительно проектного курсового угла пути К₀

α=ψ+Δα,

где ψ - угол рыскания, измеряемый ИНС. Угол поворота хорды относительно направления на Север определяется выражением

α_N=K+Δα,

где курсовой угол ИНС К=К₀+ψ.

Все входящие в выражение (8) параметры угловых и линейных перемещений элементов вагона должны быть измерены датчиками, входящими в состав измерительного комплекса. Современные путеизмерительные вагоны, например немецкий вагон OMWE, имеют такой набор датчиков. Еще лучше использовать неконтактные датчики, измеряющие непосредственно расстояние между кузовом вагона и поверхностью рельс. После выполнения всех преобразований вновь приходим к хордовому методу измерений.

Прямой переход от угла поворота измерительной хорды к координате и профилю неровностей пути возможен только в достаточно небольшом диапазоне длинных неровностей. Действительно, по аналогии с выражением (2) запишем для координат х₁ начала и х₂ конца хорды

x₁=x₀cosωt,

Связь между координатами концов хорды и углом ее поворота α устанавливается выражением

x₁-x₂=l_xtgα≈l_xα

С другой стороны,

где: - введенная выше частота следования волн неровности.

Частотная передаточная функция (координата х₁ - угол поворота хорды α) хордового устройства принимает вид

Для получения обратной передаточной функции необходимо дополнительно знать величину поступательных перемещений центра поворота хорды. Сравнивая выражения (6) и (9), нетрудно заметить, что зависимость r(λ) будет иметь тот же вид, что и график, представленный на фиг.2, если заменить а на l_x на оси абсцисс. Отсюда справедливы и все выводы, сделанные выше по недостаткам хордового метода.

Задачей изобретения является разработка бесхордового (одноточечного) способа измерений рихтовки рельсовых нитей.

Для решения поставленной задачи в способе измерения горизонтальных неровностей (рихтовки) и кривизны в плане рельсовых нитей рассчитывают текущие курсы рельсовых нитей как текущий курс кузова минус текущий угол непараллельности реборд колесных пар измерительной тележки и головок рельсовых нитей, далее получают текущие значения горизонтальных неровностей (рихтовки) рельсовых нитей как произведения базы тележки ни отклонения текущих курсов рельсовых нитей от текущих усредненных на базе тележки курсов рельсовых нитей, а текущие радиусы кривизны рельсовых нитей получают делением базы тележки на приращения курсовых углов рельсовых нитей на базе тележки.

Техническая сущность изобретения объясняется следующим.

Под рихтовкой понимаются неровности каждой из рельсовых нитей в горизонтальной плоскости по отношению к среднему положению каждой нити.

Текущий курс рельсовых нитей может быть определен как

где К_ИНСi - текущий курс кузова вагона; γ_TKi - угол виляния измерительной тележки относительно кузова; (h_li-h_2(i-n))/b_T=α_Лi - угол непараллельности реборд левых колес тележки головке левого рельса; (h_3i-h_4(i-n))/b_T=α_Пi - угол непараллельности реборд правых колес тележки головке правого рельса; h_ji - расстояние от j-той реборды до головки рельса; b_T - база тележки; n=b_T/λ_ОД; где W λ_ОД - инкремент одометра (датчика пути).

Иными словами текущий курс рельсовой нити то же, что курс тележки виртуально прижатой ребордами колес к головке рельса (на глубине 15,7 мм ниже поверхности катания рельсов).

Величины текущих горизонтальных неровностей будут иметь значения

χ_Лi=b_ТΔK_РЛi; χ_Пi=b_ТΔК_Рпi,

где - (отклонения текущих курсов рельсовых нитей от текущих усредненных значений), а усредненные на базе тележки текущие курсы, характеризующие средние положения рельсовых нитей (по азимуту)

Текущие радиусы кривизны определяются по формулам

R_лi=b_т/δК_рлi; R_пi=b_т/δК_рпi,

где δK_рлi=K_рлi-K_рл(i-n); δK_рпi=K_рпi-K_рп(i-n).

Более точными будут текущие оценки радиусов кривизны с использованием усредненных текущих курсов рельсовых нитей, а именно

где

так как в (10) исключено влияние коротких горизонтальных неровностей.

Несмотря на то, что ИНС имеет значительную погрешность (доли градуса) измерения курсового угла, точность определения горизонтальных неровностей и кривизны в плане будет высокой, так как в способе используются приращения курсовых углов, все составляющие которых измеряются с большой точностью и высокой разрешающей способностью. Приращения курсового угла кузова могут измеряться лазерным гироскопом ИНС с погрешностью менее угловой секунды. Двадцатиразрядный оптический датчик относительных угловых перемещений, измеряющий угол виляния измерительной тележки относительно кузова, имеет погрешность на уровне угловой секунды.

Погрешность измерения угла непараллельности реборд колесных пар измерительной тележки и головок рельсовых нитей определяется погрешностями оптических датчиков букса-рельс, которая не хуже ±0,1 мм. При базе тележки b_T, равной 2.4 м, она составит 17 угловых секунд. Суммарная погрешность измерения отклонения текущих курсов рельсовых нитей от текущих усредненных значений составит порядка 20 угловых секунд (9,69·10^-5 рад). Тогда погрешность измерения горизонтальных неровностей не превысит ±0,25 мм.

Таким образом, предложенный способ позволяет измерять с высокой точностью и без искажений по длине волны горизонтальные неровности рельсовых нитей, что при малом инкременте одометра позволит идентифицировать дефекты головок рельсов. Кроме того, предложенный способ позволяет с высокой точностью измерять радиусы кривизны коротких кривых участков, например стрелочных переходов (так как длина базы тележки примерно в 7 раз меньше базы вагона).

Литература

1. Вагон-путеизмеритель ЦНИИ-4. Техническое описание. ЕИМН.663511.001 Т0. - М.: 1996.

Способ измерения горизонтальных неровностей (рихтовки) и кривизны в плане рельсовых нитей, заключающийся в том, что измеряют при помощи инерциальной навигационной системы (ИНС), установленной над шкворнем измерительной тележки, текущий курс кузова путеизмерительного вагона и при помощи датчика угловых перемещений текущий угол виляния измерительной тележки относительно кузова, далее при помощи датчиков букса-рельс измеряют расстояния от реборд соответствующих колес тележки до головок рельсов, отличающийся тем, что по измерительной информации рассчитывают текущие курсы рельсовых нитей как текущий курс кузова минус текущий угол виляния измерительной тележки относительно кузова минус текущий угол непараллельности реборд колесных пар измерительной тележки и головок рельсовых нитей, далее получают текущие значения горизонтальных неровностей рельсовых нитей как произведения базы тележки на отклонения текущих курсов рельсовых нитей от текущих усредненных на базе тележки курсов рельсовых нитей, рассчитанных от курсов рельсовых нитей, а текущие радиусы кривизны рельсовых нитей получают делением базы тележки на измеренное приращение курсовых углов рельсовых нитей на базе тележки.