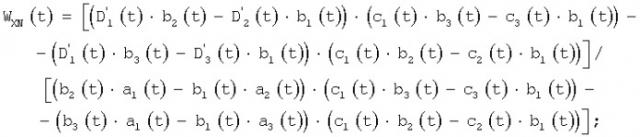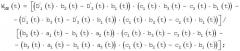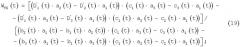Комплексный способ определения координат и параметров траекторного движения авиационно-космических объектов, наблюдаемых группировкой станций слежения

Комплексный способ определения координат и параметров траекторного движения авиационно-космических объектов, наблюдаемых группировкой станций слежения

Иллюстрации

Показать все

Реферат

Изобретение относится к области оптико-электронных, радиолокационных и иных систем сопровождения авиационно-космических объектов и может быть использовано для повышения их точности и помехоустойчивости за счет системного использования группировки этих станций.

Патентный поиск в ВПТБ проведен по классификациям G 01 S 13/00 «Системы радиолокационные - следящие», G 01 S 13/66 - 13/72, «для космических целей» B 64 G 1/24, G 01 S 17/06 - «для определения местоположения цели», 17/08 - «только дальности», 17/42 - «одновременное измерение дальности и других координат», 17/46 - «косвенное определение данных местоположения», 17/58 - «для определения скорости или траектории движения», 17/66 - «следящие системы с использованием электромагнитных волн, иных, чем радиолокационные», 17/88 - «системы лидаров».

В качестве прототипа взят наиболее близкий по технико-технологической сущности способ «определения координат целей и их производных расчетным путем», суть которого изложена в книге [1] Григорина-Рябова и др. «Радиолокационные устройства (теория и принципы построения)», М., «Советское Радио», 1970 г., стр.5÷7, 34÷39.

По прототипу в настоящее время для слежения за авиационно-космическими объектами (целями) и получения параметров их движения в основном используют различного рода трехмерные, двумерные и одномерные станции.

Трехмерные станции самостоятельно измеряют все три составляющие вектора дальности D(t) до цели [1, стр.5÷7]:

где D(t) - модуль дальности, определяемый дальномерным каналом станции;

ε(t), β(t) - углы места и азимута, определяемые угломерными каналами.

При этом векторы скорости W(t) и ускорения J(t) цели вычисляют путем дифференцирования вектора D(t):

По прототипу трехмерные станции являются датчиками полноразмерной (вектора дальности D(t), скорости W(t), ускорения J(t)) траекторной информации о наблюдаемой цели.

Заметим заранее, что от каждой i-й трехмерной станции по межстанционным дуплексным каналам информационной связи можно осуществлять полноразмерное целеуказание другой k-й станции любой размерности по векторам:

- дальности:

- скорости:

- ускорения:

где d_ki - вектор-база между k-й и i-й станциями.

Двумерными станциями пеленгационного типа измеряют только угловые координаты вектора дальности:

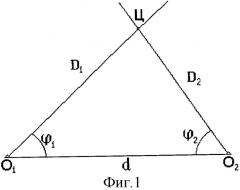
По прототипу для получения полноразмерной траекторной информации о наблюдаемой цели две двумерные станции [1, стр.34, 35] локально комплексируют с помощью межстанционных дуплексных каналов информационной связи, по которым пересылают от одной к другой измеренные значения этих углов, и, применяя теорему синусов для «треугольника O₁ЦО₂» (фиг.1), при известной базе d между двумя станциями определяют модули дальностей D₁(t) и D₂(t):

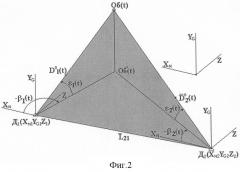
У прототипа, видимо, для простоты изложения приводятся не трехмерные, а плоскостные иллюстрации и, соответственно, формализации (7) задач локального комплексирования двух станций пеленгационного типа, когда ϕ₁(t)={β₁(t), ε₁(t)}, ϕ₂(t)={β₂(t), ε₂(t)}. Автором получен рабочий алгоритм определения по прототипу модулей дальности наблюдаемого объекта Об(t) (фиг.2) в трехмерном пространстве двумя локально скомплексированными станциями пеленгационого типа Д² ₁(Х_N1Y_G1Z₁), Д² ₂(X_N2Y_G2Z₂), где X_N, Y_G, Z - географические координаты станций. Приводим полученный основной алгоритм локального комплексирования двух станций пеленгационного типа, во-первых, для подтверждения возможностей прототипа, во-вторых, для обоснованного использования его в совокупности с дополнительными, чтобы иметь избыточное количество алгоритмов, свойственное предлагаемому изобретению. Станции удалены друг от друга на вектор-базу d=L₂₁:

В станционных системах координат Д₁(X_N1Y_G1Z₁)X_NY_GZ и Д₂(X_N2Y_G2Z₂)X_NY_GZ, соответствующие оси которых имеют одинаковые направления, синхронно измеряют углы β₁(t), ε₁(t), β₂(t), ε₂(t), значения которых пересылают от одной станции к другой по дуплексным каналам информационной связи.

Модуль дальности D₁(t) наблюдаемого объекта Об(t) относительно первой станции определяют по формулам:

Аналогичным образом с помощью подобных формул вычисляют дальность наблюдаемого объекта D₂(t) и относительно второй станции:

Как видно из представленных алгоритмов локального комплексирования (6), (8)÷(10), (2), информационное и программно-математическое единение двух станций пеленгационного типа обеспечивает получение единственных текущих значений полноразмерной траекторией информации о наблюдаемой цели.

Итак, по способу-прототипу при локальном комплексировании двух двумерных станций пеленгационного типа, во-первых, углы ϕ₁(t)={β₁(t), ε₁(t)}, ϕ₂(t)={β₂(t), ε₂(t)} измеряют в станционных системах координат, соответствующие оси которых имеют одинаковые направления, во-вторых, углы измеряют синхронно, в-третьих, измеренные значения углов пересылают от одной станции к другой по межстанционным дуплексным каналам информационной связи, в-четвертых, расчеты модулей дальностей по алгоритмам типа (8)÷(10) выполняют в станционных вычислителях, в-пятых, двумерные станции для организации локального комплексного режима каждая нуждаются в целеуказании (3) от других станций, чтобы сопровождать одну и ту же цель, в-шестых, двумерные станции автономно не могут осуществлять целеуказание ни другим станциям, ни друг-другу, и лишь устойчиво работая в комплексном режиме, способны давать единственные текущие значения полноразмерных параметров траекторного движения наблюдаемой цели и полноразмерное целеуказание (3)÷(5) другим станциям.

Одномерные станции [1, стр.35], «измеряющие только дальность» D(t), которые по прототипу в паре, применяя теорему косинусов, позволяют для цели определять «угловые координаты в плоскости треугольника O₁ЦО₂:

Заметим, что (11) у прототипа справедливо лишь для плоскостной постановки, поскольку трехмерный вектор D(t) не может быть однозначно определен в трехмерном пространстве только двумя скалярными величинами D₁(t) и D₂(t). Автором получена система рабочих алгоритмов локального комплексирования одномерно-дальномерных станций и подтверждена возможность определения ими полноразмерной траекторией информации о наблюдаемой цели в трехмерном пространстве (фиг.3), правда по данным не двух, а трех указанных станций:

где - нелинейные, неявно выраженные системы уравнений с указанными в скобках аргументами.

Алгоритм (12) и (2) подтверждает, что информационное и программно-математическое единение трех станций одномерно-дальномерного типа обеспечивает получение единственных текущих значений полноразмерной траекторией информации о наблюдаемой цели.

Видимо нет необходимости приводить в описании этот громоздкий алгоритм в развернутом виде, тем более, что процедура вычислений по нему является многошаговой, итерационной. Этот алгоритм представлен в качестве справки в Приложение №1 к описанию.

Опять отмечаем, что по способу-прототипу и для трех одномерно-дальномерных станций модули дальностей D₁(t), D₂(t), D₃(t) измеряют в станционных системах координат, соответствующие оси которых имеют определенные направления, указанные дальности измеряют синхронно, измеренные значения дальностей пересылают от одной станции к другой по межстанционным дуплексным каналам информационной связи, расчеты углов ε₁(t), β₁(t), ε₂(t), β₂(t), ε₃(t), β₃(t) по алгоритмам типа (12) (см. Приложение №1) выполняют в станционных вычислителях, одномерно-дальномерные станции для организации начальной фазы комплексного режима каждая нуждаются в целеуказании (3) от других станций, чтобы сопровождать одну и ту же цель, одномерно-дальномерные станции автономно не могут осуществлять целеуказание ни другим станциям, ни друг-другу, и лишь устойчиво работая в комплексном режиме, способны давать не только полноразмерную траекторную информацию (12), (2), но и полноразмерное (3)÷(5) целеуказание другим станциям.

Одномерные станции, определяющие «радиальную скорость» V_P(t) доплеровским методом V_P(t)=F_Д(t)·λ/2, открывают дополнительные возможности по определению в первую очередь параметров движения цели. По прототипу [1, стр.35] «Скорость движения цели W_Ц(t) удобно определять через ее ортогональные составляющие: радиальную W_P(t), направленную по линии РЛС - цель, и тангенциальную W_T(t)»:

где ω_ϕ(t) - угловая скорость цели.

«Угловая скорость цели ω_ϕ(t) может быть определена также с помощью двух РЛС, измеряющих доплеровские частотные сдвиги» [1, стр.37] F_Д1(t) и F_Д2(t):

В(13) и (14) W_Ц(t) и ω_ϕ(t) - скалярные величины (опять же плоскостная постановка и формализация задачи), а практика требует определения трехмерных векторов линейной W_Ц(t) и угловой ω_ϕ(t) скоростей наблюдаемой цели. Кроме того, угловую скорость линии «станция - цель» ω_ϕ(t) по способу-прототипу рассчитывают при допущениях, что d≤D(t)/1000, угол визирования на цель ϕ(t), отсчитываемый относительно нормали к d, в трехмерном пространстве практически не определен, а сами станции должны не просто работать на одной длине волны λ, но и быть когерентными. Указанные допущения настолько трудны, что в практике этот способ определения угловой скорости ω_ϕ(t) (15) для вычисления (13) тангенциальной составляющей скорости W_T(t) применения не нашел и мы его в указанной выше постановке исключаем из рассмотрения.

Способу-прототипу определения параметров траекторного движения объектов присущи следующие недостатки:

1. Невысокая помехоустойчивость и точность определения координат и параметров траекторного движения наблюдаемых объектов. При наличии помех или из-за частичного отказа техники станции слежения не всегда могут выполнять свои функции в полном объеме. Так, например, «уводящие по дальности» помехи могут превратить трехмерную станцию в двумерную, а одномерно-дальномерную вообще подавить, «уводящие по угловым координатам» - превратить трехмерную станцию в одномерную D(t), двумерную пеленгационного типа вообще подавить и т.д. Обычно в этих условиях происходит срыв автосопровождения и потеря информации о координатах и параметрах движения цели.

2. В систему комплексируют ограниченное количество станций: двумерных - две, а одномерных - три.

3. В систему комплексируют однородные по мерности станции: двумерную с двумерной, одномерные с одномерными.

4. Трехмерную станцию не комплексируют в систему ни с трехмерной, ни с двумерными, ни с одномерными.

5. Все комплексируемые станции для начала устойчивой совместной работы нуждаются в целеуказании (3) от других станций, чтобы обеспечить сопровождение одной и той же цели.

6. Имеющуюся избыточную информацию о наблюдаемом объекте, например о векторах дальности D₁(t), D₂(t) на локально скомплексированных двух двумерных станциях, D₁(t), D₂(t), D₃(t) на локально скомплексированных трех одномерно-дальномерных станциях, не используют для повышения точности их оценки.

7. На станциях не используют для повышения помехоустойчивости и точности прогнозирующие модели движения целей.

Цель изобретения - повысить точность и помехоустойчивость группировки станций слежения за авиационно-космическими объектами.

Указанные выше недостатки существующего способа предлагается устранить путем внедрения дополнительных, частичного использования и изменения существующих технологических приемов, в соответствии с которыми:

I. Как у способа-прототипа:

1. Используют для комплексируемых станций общую систему координат.

2. Координаты целей на комплексируемых станциях измеряют синхронно, то есть в системе единого времени (СЕВ).

3.Производят информационный обмен между скомплексированными станциями с помощью межстанционных дуплексных каналов информационной связи.

4. При определении искомых координат и параметров движения наблюдаемых объектов используют как составную часть и существующие расчетные алгоритмы локального комплексирования станций: двумерных - (8)÷(10), (2) и одномерно-дальномерных - (12) - Приложение №1, (2).

5. Искомые полноразмерные координаты и параметры движения наблюдаемых объектов рассчитывают в вычислительных машинах комплексируемых станций.

II. Дополнительные, новые:

1. Все станции группировки вне зависимости от типа их мерности соединяют межстанционными дуплексными каналами информационной связи.

2. Для обеспечения информационной совместимости вводят общую для всех станций группировки земную базисную систему координат Об(t₀)X_NY_GZ, ордината которой Об(t₀)Y_G - местная вертикаль, Об(t₀)Х_N - абсцисса, ориентирована на север, а аппликата Об(t₀)Z - завершает построение правой прямоугольной системы координат.

3. На каждую станцию по межстанционным дуплексным каналам информационной связи передают от всех станций группировки все определяемые ими текущие координаты и параметры движения целей, находящихся в зоне действия этой станции, индивидуальные номера указанных целей q, индивидуальные номера S станций Д_S(Х_NSY_GSZ_S), передающих информацию, координаты местоположения X_NS, Y_GS, Z_S которых в земной базисной системе координат заранее заложены в базы данных вычислительных машин станций группировки.

Благодаря непрерывному обмену по дуплексным каналам связи расширенной информацией о целях между станциями группировки, наличию на каждой из них избыточного количества алгоритмов комплексирования получают избыточную полноразмерную траекторную информацию о наблюдаемых целях и реализуют полноразмерное целеуказание другим станциям:

A) Для одномерно-дальномерных станций Д¹ _S(X_NSY_GSZ_S) - при получении дополнительно текущих значений углов (3) ε_kЦУ(t), βε_kЦУ(t)

и применении в качестве дополнительных алгоритмов (2) трехмерных станций.

B) Для одномерно-доплеровских станций Д^1Д _Sk(X_NSY_GSZ_S) - при получении дополнительно текущих значений (3) дальности D_kЦУ(t) и углов ε_kЦУ(t), β_kЦУ(t), k≥3 и применении (17), (20) и полученного автором нового алгоритма (18), (19) непосредственного определения вектора скорости цели по составляющим в общей земной базисной системе ДХ_NY_GZ координат, соответствующие оси которой имеют одинаковые направления со станционными системами координат Д^lД _k(X_NkY_GkZ_k)X_NY_GZ:

Модули текущих дальностей для каждой из доплеровских станций после целеуказания вычисляют методом интегрирования:

Составляющие вектора угловой скорости линии «станция - цель» в системе координат, связанной с кинематикой станции, вычисляют по формулам:

где W_ЦYD(t), W_ЦZD(t) - составляющие вектора линейной скорости цели W_Ц(t) в системе координат, связанной с кинематикой станции, полученные с помощью известной матрицы перехода М_D←1(β_kЦУ(t), ε_kЦУ(t)) от земной станционной системы координат к системе координат, связанной с кинематикой станции:

Алгоритм (17)÷(22) причисляем к существующему способу и далее используем при реализации принципа алгоритмической избыточности предлагаемого способа.

C) Для двумерных станций Д² _S(X_NSY_GSZ_S) пеленгационного типа - при получении дополнительно текущих значений (3) дальности D_kЦУ(t)

и одновременном применении избыточных алгоритмов (23), (8)÷(10), (2).

D) Для трехмерных станций Д³ _S(X_NSY_GSZ_S) - при получении дополнительно непрерывных текущих значений параметров целеуказания (3)÷(5) от других станций группировки и одновременном применении алгоритмов одномерно-дальномерных: (12) - Приложение №1 и (2), двумерных станций пеленгационного типа: (6), (8)÷(10), (2).

4. Избыточную полноразмерную траекторную информацию о каждой из целей q получают на каждой комплексируемой станции S группировки:

- по межстанционным дуплексным каналам информационной связи;

- методами непосредственных измерений;

- методами вычислений по изложенным избыточным алгоритмам.

5. На каждой комплексируемой станции S группировки выполняют статистическую обработку избыточной информации о каждой из целей q для получения оптимальных по точности оценок, например, алгоритмом текущего скользящего среднего:

где n - количество значений (переданных, измеренных, вычисленных) конкретных параметров, обрабатываемых на станции в текущий момент времени t.

6. Полученные оптимальные по точности «станционные» оценки параметров (24) используют с помощью известных алгоритмов кинематических уравнений связи и матричного преобразования (22) для формирования сигналов управления каналами станции при прерывании на время τ по какой-либо причине нормального процесса измерений станции:

- дальномерным:

- угловым азимутальным:

- угломестным:

- скоростным сближения (доплеровским):

Таким образом реализуют прогнозируемое целеуказание на каждой станции группировки. Текущее непрерывное целеуказание от других станций и собственное прогнозируемое целеуказание (25)÷(28) на каждой из станций существенно повышают их помехоустойчивость.

7. «Станционные» оценки параметров (24) в интересах дальнейшего повышения точности оценок координат и параметров движения каждой цели q передают по межстанционным дуплексным каналам связи на пункты контроля воздушно-космического пространства - потребителям информации, где представляют в земной базисной системе координат и как избыточную по множеству станций вновь статистически обрабатывают, например, по методу текущего среднего:

где S - количество станций, передавших свои текущие оценки координат и параметров движения q цели.

Источники информации

1. Системы сопровождения и определения координат искусственных спутников земли, ГК СМ СССР по радиоэлектронике, обзор, вып.28, 1961, стр.12÷29.

2. Григорин-Рябов В.В., Дудник П.И. и др. Радиолокационные устройства

(Теория и принципы построения), изд. «Советское радио», М., 1970, стр.5÷7, 34÷39.

Перечень графических материалов

1. «Определение дальности цели станциями, расположенными в двух точках O₁ и О₂».

2. Векторная схема наблюдения объекта двумя станциями пеленгационного типа в трехмерном пространстве.

3. Векторная схема наблюдения объекта тремя станциями одномерно-дальномерного типа в трехмерном пространстве.

Приложение №1

Рабочий алгоритм определения станционных углов вектора дальности при комплексировании трех одномерно-дальномерных станций

Для каждого дальномерного пункта (Фиг.3) вводят промежуточную правую прямоугольную систему координат. Ось абсцисс первого дальномерного пункта направляют вдоль вектора L₂₁, то есть на второй дальномерный пункт, орт этой оси имеет аналитическое выражение:

где «Т» - символ транспонирования.

Ось абсцисс второго дальномерного пункта ориентируют вдоль вектора L₃₂ на третий дальномерный пункт и его орт равен:

Ось абсцисс третьего пункта направляют вдоль вектора L₁₃ на первый пункт и его орт имеет выражение:

Аналитические выражения для осей ординат получают с помощью векторных произведений:

где

Аналогичным образом получают аналитические выражения для аппликат:

Матрицы перехода при повороте от с.к., связанных с дальномерными пунктами, к земной с.к. формально имеют вид:

где i - номер дальномерного пункта.

На основании изложенного получают аналитические выражения для всех направляющих косинусов матриц перехода (11п):

После геодезической привязки дальномерных пунктов к земной с.к. производят однократные вычисления по алгоритмам (1п)÷(14п) в интересах определения всех указанных констант, включая направляющие косинусы матрицы преобразования при поворотах (11п)÷(14п) и константы алгоритма (15п) полного преобразования координат положения при переходе от с.к., связанных с дальномерными пунктами, к земной с.к. с учетом как поворота, так и смещения с.к.:

Далее используют алгоритм итерационного поиска значений углов (см. рис.3) β₁(t) и ε₁(t), β₂(t) и ε₂(t), β₃(t) и ε₃(t). При каждом состоявшемся синхронном измерении модулей дальностей D₁(t), D₂(t), D₃(t) их значения подставляют в систему уравнений:

Алгоритм итерационного процесса решения полученных уравнений:

1. Вводят необходимые константы L₂₁, L₃₂, L₁₃, γ₁, γ₂, γ₃, S_Δ и начальные t₀ условия D₁(t₀), D₂(t₀), D₃(t₀).

2. Организуют «нулевой» цикл для определения β₁(t₀) и ε₁(t₀), β₂(t₀) и ε₂(t₀), β₃(t₀) и ε₃(t₀):

2.1. С помощью уравнения (19п) вычисляют в явном виде sin(β₁(t)), затем β₁(t), cos(β₁(t)) и cos(β₁(t)-γ₁).

2.2. Подставляют cos(β₁(t)) и cos(β₁(t)-γ₁) в уравнения (16п) и (17п), sin(β₁(t))

- в уравнение (19п), β₁(t) - используют для оценки сходимости итерационного процесса решения.

2.3. Вновь с помощью уравнения (19п) вычисляют в явном виде, но теперь sin(β₂(t)), затем β₂(t), cos(β₂(t)) и cos(γ₂-β₂(t)).

2.4. Подставляют cos(β₂(t)) и cos(γ₂-β₂(t)) в уравнения (17п) и (18п), sin(β₂(t))

- в уравнение (19п), β₂(t) - используют для оценки сходимости итерационного процесса решения.

2.5. Опять же с помощью уравнения (19п) вычисляют в явном виде, но теперь sin(β₃(t)), затем β₃(t), cos(β₃(t)) и cos(γ₃-β₃(t)).

2.6. Подставляют cos(β₃(t)) и cos(γ₃-β₃(t)) в уравнения (18п) и (16п), sin(β₃(t))

- в уравнение (19п), β₃(t) - используют для оценки сходимости итерационного процесса решения.

2.7. Решают сгруппированные уравнения (16п), (17п) в интересах получения cos(ε₁(t)), затем ε₁(t):

2.8. Подставляют cos(ε₁(t)) в уравнения (16п), (17п) и (19п), a ε₁(t) - используют для оценки сходимости итерационного процесса решения.

2.9. Решают сгруппированные уравнения (17п), (18п) в интересах получения cos(ε₂(t)), затем ε₂(t):

2.10. Подставляют cos(ε₂(t)) в уравнения (17п), (18п) и (19п), а ε₂(t) - используют для оценки сходимости итерационного процесса решения.

2.11. Решают сгруппированные уравнения (18п), (16п) в интересах получения cos(ε₃(t)), затем ε₃(t):

2.12. Подставляют cos(ε₃(t)) в уравнения (18п), (16п) и (19п), а ε₂(t) - используют для оценки сходимости итерационного процесса решения.

2.13. Повторяют п.п.2.1.÷2.12 второй раз и находят разности δβ₁(t), δε₁(t):

δβ₁(t)=β₁(t)_НОВ-β₁(t)_СТ; δβ₂(t)=β₂(t)_НОВ-β₂(t)_СТ; δβ₃(t)=β₃(t)_НОВ-β₃(t)_СТ;

δε₁(t)=ε₁(t)_НОВ-ε₁(t)_СТ; δε₂(t)=ε₂(t)_НОВ-ε₂(t)_СТ; δε₃(t)=ε₃(t)_НОВ-ε₃(t)_СТ.

Если хотя бы одна из разностей оказалась по модулю больше допустимого значения δ_ДОП, то цикл итераций (п.п.2.1.÷2.12) повторяют.

3. При сходимости итерационного процесса вычислений по точности находят проекции теперь уже векторов дальности сначала на оси с.к. дальномерных пунктов, а затем (15п) на оси земной с.к... Причем составляющие итогового вектора дальности в с.к. «G» берут как среднее из трех получаемых значений.

4. Переходят к обработке очередных синхронных измерений модулей дальностей D₁(t), D₂(t), D₃(t), а в качестве начальных значений для итерационного поиска углов β₁(t), β₂(t), β₃(t), ε₁(t), ε₂(t), ε₃(t) берут их итоговые значения из предыдущего завершившегося цикла вычислений.

Комплексный способ определения координат и параметров траекторного движения авиационно-космических объектов, наблюдаемых группировкой станций слежения, заключающийся в том, что на взаимодействующих станциях в единых системах координат, соответствующие оси которых имеют одинаковые направления, синхронно измеряют координаты наблюдаемых объектов, значения которых передают друг другу с помощью межстанционных дуплексных каналов информационной связи, вычисляют в станционных вычислителях с учетом известных базовых расстояний между станциями, измеренных и переданных координат наблюдаемых объектов по расчетным алгоритмам локального комплексирования единственные текущие значения информации о параметрах траекторного движения наблюдаемых объектов, отличающийся тем, что межстанционными дуплексными каналами информационной связи соединяют все станции группировки вне зависимости от типа их мерности для обмена всеми измеряемыми, вычисляемыми на них данными о параметрах траекторного движения наблюдаемых объектов, с их индивидуальными номерами и номерами станций, передавших упомянутую информацию, координаты местоположения которых заданы в единой земной базисной системе координат, на каждой станции группировки реализуют избыточное количество алгоритмов локального комплексирования, с помощью которых получают избыточную информацию о параметрах траекторного движения наблюдаемых объектов, которую в станционных вычислителях каждой комплексируемой станции группировки статистически обрабатывают и получают оптимальные по точности оценки этой информации о параметрах траекторного движения наблюдаемых объектов, далее на основе этих оценок по известным алгоритмам кинематических уравнений связи и матричного преобразования формируют сигналы управления дальномерными и угломерными каналами станций при прерывании на некоторое время по какой-либо причине нормального процесса их функционирования, а также оценки информации о параметрах траекторного движения наблюдаемых объектов передают по межстанционным дуплексным каналам связи на пункты контроля воздушно-космического пространства, где их представляют в единой земной базисной системе координат и как избыточные по множеству станций вновь статистически обрабатывают и получают уточненные оценки информации о параметрах траекторного движения наблюдаемых объектов.