Вычислительный модуль и способ выполнения арифметической операции с зашифрованными операндами

Вычислительный модуль и способ выполнения арифметической операции с зашифрованными операндами

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к устройствам обработки данных и, в частности, к устройствам обработки данных, требующим обработки данных или адресов на высоком уровне защищенности, обеспечивающим защиту от физических атак и перехвата.

При вычислении и/или обработке данных, связанных с необходимостью обеспечения защиты, используются микропроцессоры или маркеры доступа или другие устройства обработки данных с высоким уровнем защищенности, обеспечивающим защиту от физических атак и перехвата. Блоки кэш-памяти и буферной памяти, наборы регистров, а также каналы передачи, например, в виде шин, на микропроцессорах, представляют собой регулярные структуры на кристалле, которые легко идентифицировать. Таким образом, они представляют собой предпочтительные точки атаки. Атаки могут состоять в перехвате посредством атак на выводах или в анализе профиля тока.

Методы шифрования позволяют эффективно защищать блоки внешней памяти, блоки буферной памяти и шины, в результате чего, обрабатываемые данные, например, пользовательские данные или программы, перемещаются и сохраняются на всем кристалле, предпочтительно, только в зашифрованном виде.

На фиг.10 показана общая схема вычислительного устройства. Главным блоком вычислительного устройства является арифметико-логическое устройство (АЛУ) 800. Простейшее АЛУ, способное выполнять операцию с двумя операндами, требует двух входных шин А, В (802, 804) и выходной шины Z (806). Входные шины и выходная шина АЛУ 800 присоединены к главной шине F (808). К главной шине (808) обычно также подключены две дополнительные шины D, E (810, 812), причем шина 810 подключена к кэшу М2 (814), который, в свою очередь, подключен к внешней памяти М1 (812) через шину памяти С (816). Кроме того, согласно варианту осуществления, показанному на фиг.10, вычислительное устройство содержит наборы регистров М3 (820), причем каждый набор регистров содержит регистры, в которых могут храниться (первоначально) входные данные АЛУ или выходные данные АЛУ, не подлежащие переносу в кэш 814 или во внешнюю память 818, т.е. не подлежащие загрузке из наборов регистров во внешнюю память до окончания сравнительно долгого вычисления.

В вычислительном устройстве, осуществляющем вычисления, критические с точки зрения обеспечения защищенности, данные шифруются до сохранения в различных блоках памяти М1-М3. Кроме того, во избежание атаки на шинные линии 802, 804, 806, 810, 812 и 816, предпочтительно передавать данные по этим шинным линиям в зашифрованном виде. В этом случае, на двух входах АЛУ предусмотрены две схемы 822, 824 дешифрования для дешифрования операндов, присутствующих на шинах А, В, например, данных или адресов, подлежащих обработке на АЛУ 800, перед их обработкой. Для защиты результата операции АЛУ, на выходе АЛУ 800 предусмотрено устройство 826 шифрования, поэтому на шинах 802, 804, 806 присутствуют зашифрованные данные.

Хотя эта концепция позволяет эффективно подавлять атаки на шинные линии, например, главную шину 808, а также шины 810, 812, 816 памяти, она обладает тем недостатком, что между двумя схемами 822, 824 дешифрования и схемой 826 шифрования присутствуют незащищенные данные открытого текста, поэтому, хотя атакующему труднее выяснить, где в вычислительном устройстве находится АЛУ 800, задача атакующего значительно облегчается, когда он определит местоположения устройств дешифрования, поскольку на выходах устройств 822 и 824 дешифрования присутствуют данные открытого текста.

С другой стороны, данные нужно дешифровать, поскольку операции АЛУ, которые могут представлять собой, например, простые арифметические операции, например, И, ИЛИ, «исключающее или», НЕ-И, НЕ-ИЛИ, НЕ или «сложение», нельзя просто осуществлять над зашифрованными данными, поскольку операции шифрования и дешифрования и простая операция в общем случае не коммутируются, что приводит к искажению результатов. Чтобы, тем не менее, закрыть этот пробел в защите, устройства 822, 824 дешифрования и устройство 826 шифрования обычно предпочитают размещать как можно ближе к АЛУ 800, чтобы линии передачи, по которым идут данные открытого текста, были как можно короче, что позволяет снизить эффективность атаки. Альтернативно, линии передачи, по которым передаются данные открытого текста, можно «скрывать» в кристалле с использованием технологических мер, например, с использованием особых профилей легирования или с использованием совокупности ложных линий, из-за чего атакующему приходится выявлять линии, по которым фактически передаются данные открытого текста, в отличие от ложных линий, по которым передаются только диверсионные, т.е. фальшивые, данные.

Эти традиционные меры защиты вычислительного устройства от атак сталкиваются с той проблемой, что они требуют дополнительных затрат и ограничивают свободу в разработке АЛУ. Ограничение свободы конструкции является недостатком, в частности, если АЛУ должно быть высокопроизводительным АЛУ, которое призвано выполнять совокупность вычислений, в частности, например, расчеты с длинными числами. Чтобы, тем не менее, поддерживать время вычисления в разумных пределах, АЛУ следует конструировать с учетом оптимизации производительности. Конечно, клиент вправе ожидать от любой системы защиты высокого уровня защищенности. Однако, в то же время, клиент также ожидает приемлемо продолжительного, предпочтительно, короткого времени вычисления. Короткое время вычисления важно, чтобы система защиты была принята на рынке, поскольку долгое время вычисления в идентификации защиты будет рассматриваться клиентом как раздражающий фактор.

Задачей настоящего изобретения является обеспечение простой и недорогой концепции реализации выполнения операции на зашифрованном операнде, сумматора с выборочным переносом для зашифрованных данных, а также криптографического процессора, который, тем не менее, обеспечивает высокий уровень защиты от атак. Для решения этой задачи предусмотрены вычислительное устройство, заявленное в пункте 1 формулы изобретения, способ, заявленный в п.27, криптографический процессор, заявленный в п.28, и способ или устройство для формирования средства вычислительного устройства, заявленный/ое в п.36 и/или в п.37.

Настоящее изобретение основано на том, что наивысшего уровня защищенности можно достичь, когда вычислительное устройство работает с полностью зашифрованными операндами, в связи с чем на входе обрабатывающего устройства не осуществляется дешифрование, и на выходе обрабатывающего устройства или АЛУ не осуществляется шифрование. Согласно изобретению, реализация АЛУ предусматривает, помимо входа для первого зашифрованного операнда и входа для второго зашифрованного операнда, наличие третьего входа для параметра шифрования, причем реализация АЛУ позволяет связывать зашифрованные операнды и параметры шифрования в соответствии со спецификацией вычисления над шифрованным текстом с учетом того, каким образом зашифрованы два операнда, в результате чего на выходе получается зашифрованный результат, равный значению, которое можно было бы получить, подвергнув первый операнд арифметической операции в соответствии со спецификацией вычисления над открытым текстом в незашифрованном виде и подвергнув второй операнд арифметической операции в соответствии со спецификацией вычисления над открытым текстом в незашифрованном виде, а затем зашифровав полученный результат. Другими словами, арифметическая операция, подлежащая выполнению над двумя зашифрованными операндами, например, операция OR (ИЛИ) в качестве спецификации вычисления над открытым текстом заменяется несколькими арифметическими подоперациями, формирующими спецификацию вычисления над шифрованным текстом, причем арифметические подоперации выбираются так, чтобы они имели на входе зашифрованные операнды либо инвертированные зашифрованные операнды и параметр шифрования либо инвертированный параметр шифрования.

При необходимости, можно предусмотреть дополнительные подоперации, имеющие на входе промежуточные результаты, полученные из зашифрованных входных операндов и ключа, так что входные операнды в виде открытого текста сами по себе нигде не присутствуют в АЛУ. Для повышения уровня защищенности, предпочтительно, чтобы не существовало также никаких промежуточных результатов из входных операндов в виде открытого текста. На примере операции ИЛИ это означает, что зашифрованные операнды и параметр шифрования подвергаются нескольким операциям AND (И) и нескольким операциям OR (ИЛИ) и, при необходимости, операциям отрицания (инвертирования), в результате чего АЛУ выдает результат, который равен результату, который был бы получен, если бы зашифрованные входные операнды были бы сначала дешифрованы, затем подвергнуты единичной операции ИЛИ, а затем повторно зашифрованы.

В случае использования метода шифрования, состоящего из алгоритма шифрования и ключа, для каждого алгоритма шифрования получается отдельная структура АЛУ для арифметической операции. В этом случае, уровень защищенности может возрастать просто за счет смены ключа алгоритма шифрования, либо для каждой операции, либо через несколько операций, что имеет преимущество в том, что изменяющиеся ключи можно использовать в случае идентичной структуры АЛУ, что еще больше затрудняет для атакующего извлечение данных открытого текста, например, из структуры АЛУ.

Иными словами, реализация обрабатывающего блока вычислительного устройства, отвечающего изобретению, позволяет выполнять одну или несколько математических подопераций, которые, совместно, обеспечивают спецификацию вычисления, выведенную из спецификации для операции с незашифрованными операндами, так что, по меньшей мере, один незашифрованный операнд, из которого получается, по меньшей мере, один зашифрованный операнд, заменяется математической комбинацией, по меньшей мере, одного зашифрованного операнда и параметра шифрования, причем математическая комбинация является обратной по отношению к алгоритму шифрования, с помощью которого зашифрован зашифрованный операнд.

Посредством математической комбинации, спецификация вычисления над открытым текстом преобразуется в спецификацию вычисления над шифрованным текстом, содержащую одну или несколько математических подопераций, которые получают, в качестве входной величины, только зашифрованный операнд или его инвертированную версию, или комбинацию зашифрованного операнда и/или его инвертированной версии с другими операндами. Незашифрованный операнд сам по себе нигде не появляется в качестве входной величины для математической подоперации и, потому, не может быть перехвачен.

Ясно, что спецификация вычисления над шифрованным текстом, которая получается из одного или нескольких математических подопераций, может быть реализована любым желаемым способом. Иными словами, это значит, что математические подоперации, которые совместно формируют спецификацию вычисления над шифрованным текстом, могут быть любого рода. Необходимо только, чтобы совместно они формировали именно ту спецификацию вычисления над шифрованным текстом, которая обеспечивает те же результаты, что и соответствующая спецификация вычисления над открытым текстом после шифрования результата.

Еще одно предварительное условие состоит в том, чтобы алгоритм шифрования, с помощью которого шифруется, по меньшей мере, один операнд, был обратимым алгоритмом шифрования. Если алгоритм шифрования является, например, побитовой функцией «исключающее ИЛИ» (XOR) или функцией «исключающее НЕ-ИЛИ» (XNOR), то алгоритм, обратный алгоритму шифрования, прост. Это также будет, опять же, функция «исключающее ИЛИ» и/или «исключающее НЕ-ИЛИ».

Концепция изобретения, в принципе, может быть реализована для любого обратимого алгоритма шифрования, в зависимости от степени сложности, который может быть оправдан в каждом случае. Простейшая реализация зашифрованного вычислительного устройства состоит в использовании побитовой операции XOR с ключом в качестве алгоритма шифрования, поскольку алгоритм, обратный алгоритму шифрования, опять же, представляет собой операцию «исключающее ИЛИ» с тем же ключом. Конечно, то же справедливо для функции «исключающее НЕ-ИЛИ».

В предпочтительных вариантах осуществления настоящего изобретения, сам по себе алгоритм шифрования является, опять же, побитовой арифметической операцией, например, операцией «исключающее ИЛИ» или «исключающее НЕ-ИЛИ». С учетом правил преобразования для арифметических операций, можно найти арифметическое уравнение, и, начиная с арифметической операции, подлежащей вычислению, и с алгоритма шифрования, причем в уравнении имеются не операнды в виде открытого текста, а зашифрованные операнды, логически связанные друг с другом и/или с параметром шифрования с использованием подопераций, чтобы обеспечить, опять же, тот же результат, который был бы получен, если бы входные параметры были бы сначала дешифрованы, затем подвергнуты арифметической операции, а затем снова зашифрованы.

Преимущество настоящего изобретения состоит в том, что в вычислительных устройствах, отвечающих изобретению, нигде нет операндов в виде открытого текста, а присутствуют только зашифрованные операнды. Таким образом, атакующий уже не может перехватить операнды в виде открытого текста в каком-либо месте вычислительного устройства.

Еще одно преимущество настоящего изобретения состоит в том, что, если метод шифрования, для которого реализовано вычислительное устройство, отвечающее изобретению, используется для сохранения данных в памяти, то никакие данные открытого текста уже не присутствуют ни в каком месте компьютера, но видны только зашифрованные данные и параметры шифрования. Если вычислительное устройство, отвечающее изобретению, реализовано на плате с микросхемами, для которой не гарантировано постоянное пребывание в защищенной среде, но напротив, она может оказаться в руках атакующего и в полном его распоряжении, атакующий никоим образом не может получить из платы с микросхемами никаких данных открытого текста, поскольку там находятся только зашифрованные данные. Данные открытого текста, подлежащие обработке, будут, таким образом, шифроваться в защищенной среде прежде, чем будут загружены в плату с микросхемами, и в качестве защищенной среды выступает, например, стационарный терминал, который может представлять собой, например, устройство для выдачи наличности, доступ к которому разрешен только определенным лицам. Структура интерфейса к плате с микросхемами не позволяет атакующему извлечь данные открытого текста из устройства выдачи наличности, поскольку данные открытого текста зашифрованы на защищенном терминале прежде, чем поступили на интерфейс к плате с микросхемами, и, поскольку защищенный терминал шифрует данные открытого текста таким образом, в частности, потому, что алгоритм шифрования согласуется со структурой АЛУ на плате с микросхемами. При этом, ни в одном месте не требуется двустороннего шифрования, вследствие чего получается фактически замкнутая система. Эту замкнутую систему легко защитить, если место, где в систему вводятся данные открытого текста, находится в надежной среде.

Еще одно преимущество настоящего изобретения в том, что АЛУ может быть реализовано различными способами в зависимости от имеющейся технологии изготовления кристаллов. Например, подоперации можно выбирать по-разному, в зависимости от правил арифметики, которая может быть, например, двоичной, чтобы всегда выдавать один и тот же результат, т.е. одну и ту же таблицу истинности. Если существует полная система, например, НЕ-И (NAND) или НЕ-ИЛИ (NOR), то может быть найдена соответствующая реализация.

Если, например, существуют только вентили НЕ-И, которые имеют всего лишь два входа, то можно найти реализацию, в которой присутствуют только вентили НЕ-И с двумя входами. Если же присутствуют вентили НЕ-И или вентили НЕ-ИЛИ, имеющие несколько входов, и, если, дополнительно, можно простым способом реализовать операции НЕ (NOT), то такую же таблицу истинности можно реализовать с использованием совокупности других связей и подопераций. Эту гибкость или изменяемость можно дополнительно использовать для нахождения наиболее подходящей компоновки в плане конструкций схем и времени вычисления или для использования сменных компоновок для одних и тех же вычислительных устройств, чтобы дополнительно сбить с толку потенциальных атакующих, желающих, например, сравнить несколько плат с микросхемами для получения секретной информации.

В наиболее общем случае, только операнд операции, подлежащей выполнению вычислительным устройством, является зашифрованным операндом, тогда как другие операнды являются операндами в виде открытого текста. Это уже обеспечивает определенный уровень защищенности в арифметической и/или логической операции, поскольку результат операции И между первым параметром «а» и вторым параметром «b» уже зашифрован, если только один из операндов, т.е. «а» или «b», зашифрован.

Альтернативно, оба операнда могут быть зашифрованы одним и тем же и/или разными алгоритмами шифрования, или одним алгоритмом шифрования, но с разными ключами.

Вычислительное устройство, отвечающее изобретению, может быть также выполнено с возможностью осуществления операции мультиплексирования, в которой, по меньшей мере, один операнд, который зашифрован, является управляющим сигналом. Мультиплексор, имеющий зашифрованный управляющий сигнал, может либо мультиплексировать незашифрованные входные данные зашифрованным способом, либо мультиплексировать зашифрованные входные данные зашифрованным способом. В зависимости от размера мультиплексора, управляющий сигнал имеет длину всего лишь одного бита, т.е. в случае мультиплексора 2:1. Для мультиплексоров большего размера, управляющий сигнал может иметь длину в 2 или несколько битов. В зависимости от нужного стандарта защиты, каждый бит управляющего сигнала может быть зашифрован своим собственным ключом, или все биты управляющего сигнала могут быть зашифрованы одним и тем же ключом.

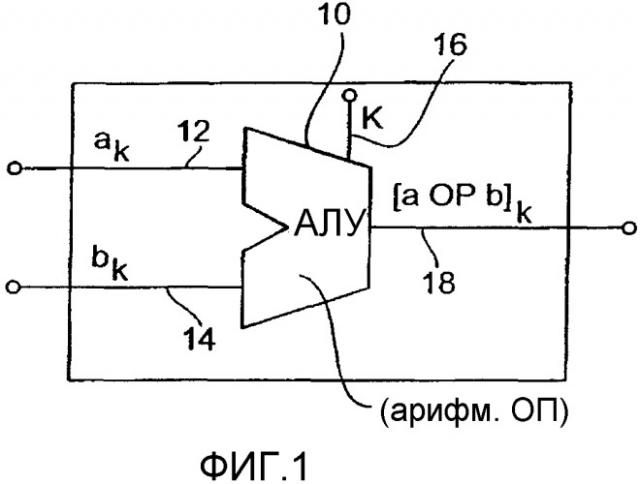
Фиг.1 - схема вычислительного устройства, отвечающего изобретению.

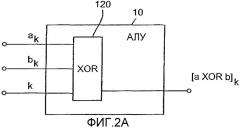
Фиг.2а - реализация вычислительного устройства, отвечающего изобретению, для шифрования посредством побитовой операции «исключающее ИЛИ» операндов и, таким образом, для реализации на АЛУ операции «исключающее ИЛИ».

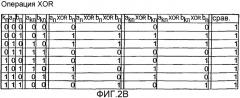
Фиг.2b - таблица истинности для схемы, показанной на фиг.2а.

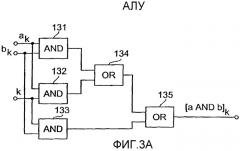
Фиг.3а - схема АЛУ для вычислительного устройства, отвечающего изобретению, для реализации операции И, где операнды зашифрованы посредством операции «исключающее ИЛИ».

Фиг.3b - таблица истинности для схемы, показанной на фиг.3а.

Фиг.4а - схема АЛУ для вычислительного устройства, отвечающего изобретению, для реализации операции ИЛИ, где операнды зашифрованы посредством операции «исключающее ИЛИ».

Фиг.4b - таблица истинности для схемы, показанной на фиг.4а.

Фиг.5а - схема АЛУ для вычислительного устройства, отвечающего изобретению, для реализации операции НЕ-ИЛИ, где операнды зашифрованы посредством операции «исключающее ИЛИ».

Фиг.5b - таблица истинности для схемы, показанной на фиг.5а.

Фиг.6а - схема АЛУ для вычислительного устройства, отвечающего изобретению, для реализации операции НЕ-И, где операнды зашифрованы посредством операции «исключающее ИЛИ».

Фиг.6b - таблица истинности для схемы, показанной на фиг.6а.

Фиг.7а - схема АЛУ для вычислительного устройства, отвечающего изобретению, для реализации операции «сложение» для трех операндов, где три операнда зашифрованы посредством операции «исключающее ИЛИ».

Фиг.7b - таблица истинности для схемы, показанной на фиг.7а, в отношении переносов.

Фиг.8а - блок-схема мультиплексора 2:1 с зашифрованным управляющим сигналом.

Фиг.8b - блок-схема мультиплексора 3:1 с зашифрованным управляющим сигналом.

Фиг.8с - блок-схема мультиплексора 4:1 с зашифрованным управляющим сигналом.

Фиг.8d - пример реализации мультиплексора 2:1 с зашифрованным управляющим сигналом.

Фиг.9а-9с - блок-схемы вычислительного устройства, отвечающего изобретению, реализованного в качестве сумматора, где операнды шифруются с помощью разных ключей и переносы зашифрованы по-разному.

Фиг.10 - вычислительное устройство, отвечающее уровню техники, с дешифрованием на входе АЛУ и шифрованием на выходе АЛУ.

Фиг.11а - блок-схема криптопроцессора, отвечающего изобретению, имеющего вычислительное устройство, отвечающее изобретению.

Фиг.11b - более подробное представление устройства шифрования/дешифрования, показанного на фиг.11а.

Фиг.12а - схема двух битовых секций сумматора, причем каждая битовая секция содержит 1-битовый полный сумматор в качестве вычислительного устройства, отвечающего изобретению.

Фиг.12b - обобщенная блок-схема сумматора со сквозным переносом для зашифрованных данных.

Фиг.13 - блок-схема сумматора с выборочным переносом для зашифрованных данных с выборочным переносом в области шифрованного текста.

На фиг.1 показано вычислительное устройство, отвечающее изобретению, для выполнения арифметической операции над, по меньшей мере, двумя операндами, причем, по меньшей мере, два операнда являются зашифрованными операндами a_k и b_k. Вычислительное устройство, отвечающее изобретению, содержит арифметико-логическое устройство АЛУ 10, которое содержит, помимо первого входа 12 для первого зашифрованного операнда a_k, второй вход 14 для второго зашифрованного операнда b_k. АЛУ 10, отвечающее изобретению, дополнительно содержит третий вход 16 для параметра шифрования k, а также выход 18 для вывода зашифрованного результата арифметической операции ОП (ОР), осуществляемой АЛУ 10. Арифметико-логическое устройство 10 позволяет связывать первый вход 12, второй вход 14 и третий вход 16 для параметра шифрования k с учетом вида шифрования операндов a_k, b_k, с использованием арифметических подопераций таким образом, что на выходе получаются зашифрованный результат, который равен значению, можно было бы получить, подвергнув первый операнд «а» арифметической операции ОП в незашифрованном виде и подвергнув второй операнд «b» арифметической операции ОП в незашифрованном виде, а потом зашифровав полученный результат, что представлено квадратными скобками и индексом k на фиг.1. В арифметико-логическом устройстве 10 не осуществляется никакого дешифрования операндов a_k и b_k, но имеют место только такие подоперации, которые выполняются над зашифрованными операндами a_k, b_k и над параметром шифрования k или над инвертированными зашифрованными операндами, или над инвертированным параметром шифрования, или над промежуточными результатами предыдущих операций.

Описанное арифметико-логическое устройство, отвечающее изобретению, позволяет выполнять арифметико-логические операции непосредственно над зашифрованными данными и выводить результат также в зашифрованном виде. При этом, предпочтительно, также гарантируется, что ни в каком промежуточном результате не появляется открытый текст. Таким образом, реализуется структура процессора, обеспечивающая работу в полностью зашифрованном режиме в сочетании с зашифрованным хранением.

АЛУ 10, отвечающий изобретению, позволяет осуществлять все манипуляции в ЦП с зашифрованными данными. На нижеследующих чертежах простые операции АЛУ, такие, как «сложение», И, ИЛИ, НЕ, НЕ-И, НЕ-ИЛИ и «исключающее ИЛИ», представлены лишь в порядке примера. При этом данные на всех шинах (фиг.10), а также в блоках памяти М1-М3 (фиг.10) предполагаются зашифрованными.

Исключительно в порядке примера, в качестве простого метода шифрования на шинах A-F, показанных на фиг.10, используется побитовая операция «исключающее ИЛИ» над предпочтительно временным ключом k_n и данными, однако и этот метод шифрования обеспечивает защиту вследствие возможности осуществления частой смены ключа. В данном случае n - это индекс ключа. Ключ k_n предпочтительно является временным и область его действия ограничена, например, только одной или несколькими последовательными операциями. Для простейшего ЦП требуются две входные шины А, В, которые представляют собой две входные линии 12, 14, показанные на фиг.1. Данные на обеих шинах побитово шифруются одним и тем же ключом k_n в целях упрощенного представления. Однако, на двух входах 12, 14, показанных на фиг.1, можно, конечно, использовать разные ключи. Кроме того, не обязательно использовать побитовое шифрование, но можно также шифровать, например, каждый второй, каждый четвертый, каждый шестой или каждый восьмой бит, оставляя перемежающие биты незашифрованными. Определенного уровня шифрования можно достичь, зашифровав только один бит операнда или один единственный разряд операнда, оставив другие разряды незашифрованными.

Хотя на нижеследующих фиг. 2а-7b в качестве основы всегда предполагается шифрование посредством побитового «исключающего ИЛИ» с ключом k_n, очевидно, что в качестве алгоритма шифрования можно использовать любую другую обратимую операцию, например, операцию «исключающее НЕ-ИЛИ». Кроме того, в качестве алгоритмов шифрования можно использовать любые другие обратимые алгоритмы шифрования. Единственное предварительное условие состоит в том, что нужно найти выражения, в которых только зашифрованные операнды a_k, b_k и параметр шифрования k существуют в состоянии, когда они подверглись некоторой логической обработке, например, инвертированы или связаны или появляются в общем случае в математической функции, что становится очевидным при обзоре математических законов, например, правил эквивалентности для арифметических вычислений по аналогии с приведенными ниже примерами.

Как уже было объяснено, для нижеследующих иллюстративных реализаций АЛУ 10, отвечающего изобретению, в целях упрощения представления, предполагается шифрование операндов «а» и «b» посредством побитового «исключающего ИЛИ», причем зашифрованные операнды и/или зашифрованные результаты обозначаются индексом k, параметр шифрования обозначается k, и индекс n является индексом счета для n-го бита соответствующего операнда и/или ключа. Зашифрованные биты на входе вычислительного устройства, отвечающего изобретению, вычисляются следующим образом:

	(1a)
	(2a)

Уравнения, обратные уравнениям (1а) и (2а) (уравнения дешифрования), таковы:

	(1b)
	(2b)

Следующее вычисление вытекает из этого для операции «исключающее ИЛИ», т.е., скажем, если АЛУ должно выполнять операцию «исключающее ИЛИ»:

(3)

Нижеследующее уравнение 4 доказывает уравнение 3.

(4)

На фиг.2а представлена схемотехническая реализация уравнения 3. Для обеспечения результата, который эквивалентен операции «исключающее ИЛИ» над незашифрованными операндами a, b и последующему шифрованию, АЛУ 10 в этом случае содержит для выполнения арифметико-логических подопераций тройной вентиль 120 «исключающее ИЛИ», который связывает друг с другом зашифрованные входные параметры a_k, b_k и k. Таким образом, можно видеть, что параметры «а» и «b» открытого текста не присутствуют нигде в АЛУ 10, показанном на фиг.2а.

В реализации тройного вентиля «исключающее ИЛИ» гарантируется, что на внутренней линии нет никаких данных открытого текста. Например, запрещено использовать двухкаскадные двойные вентили «исключающее ИЛИ», поскольку в этом случае могут появиться промежуточные результаты открытого текста. Поэтому, для реализации тройного вентиля «исключающее ИЛИ» предпочтительно использовать таблицу перекодировки, имеющую, в качестве входных параметров, значения, представленные на фиг.2b для входных параметров k_n, a_kn и b_kn и (a_n XOR b_n XOR k_n). Таблица может быть реализована в ПЗУ.

Следует указать, что реализация операции «исключающее ИЛИ», показанная на фиг.2а, является лишь иллюстративной. Конечно, выражение, представленное в середине уравнения (4), также можно реализовать схемотехническими средствами. В этом случае, потребуются четыре соответствующим образом соединенных вентиля «исключающее ИЛИ». Хотя эта реализация затратна в отношении схемотехники и времени вычисления, ее, тем не менее, можно выбрать для того, чтобы ввести в заблуждение потенциальных атакующих.

На фиг.2b представлена таблица истинности. В первых трех столбцах представлены все возможные комбинации ключа k, первого операнда «а» и второго операнда «b». В столбцах №4 и №5 показаны зашифрованные входные операнды для всех возможных комбинаций битов. В столбце №6 показан результат операции «исключающее ИЛИ» для двух незашифрованных операндов a и b. В седьмом столбце показан результат, который получается в результате перешифрования выхода операции «исключающее ИЛИ» над незашифрованными операндами, что можно реализовать, например, посредством схемы 826 на фиг.10.

В восьмом столбце на фиг.2b показан результат первой арифметической подоперации 120. В предпоследнем столбце на фиг.2b показан результат второй подоперации 122, сравнение девятого столбца с седьмым столбцом на фиг.2b подтверждает правильность связи с арифметическими подоперациями.

На фиг.3а представлена реализация вычислительного устройства, отвечающего изобретению, в котором АЛУ выполняет операцию И. На фиг.3b представлена соответствующая таблица истинности. В нижеследующем уравнении (5) указан путь от операции И над незашифрованными операндами «а» и «b» с последующим шифрованием посредством «исключающего ИЛИ», что можно реализовать посредством схемы, показанной на фиг.10, к реализации настоящего изобретения, заданной, например, последней строкой уравнения (5). АЛУ, выполняющее операцию И, включает в себя всего пять подопераций 131-135, которые являются операциями И и операциями ИЛИ. Таблица истинности на фиг.3b подтверждает правильность реализации АЛУ, отвечающего изобретению, с использованием нескольких арифметико-логических операций для связывания зашифрованных операндов и ключа. Здесь уместно отметить, что любая из промежуточных строк уравнения (5) может быть реализована схемотехническими средствами в зависимости от того, какие вентили доступны разработчику схемы, и в зависимости от допустимых вычислительных затрат. Предполагается, что схемотехническая реализация, показанная на фиг.3а, более эффективна в отношении времени вычислений, чем схемотехническая реализация, например, четвертой строки уравнения (5). Однако, эту реализацию также можно использовать, чтобы вводить в заблуждение потенциальных атакующих, как уже было показано ранее.

(5)

Ниже даются ссылки на уравнение (5) для представления основной предложенной концепции создания средства вычислительного устройства посредством преобразования спецификации вычисления над открытым текстом в спецификацию вычисления над шифрованным текстом. Операция И обеспечена как спецификация вычисления над открытым текстом.

Кроме того, предполагается, как в случае уравнения (5), что зашифрованный операнд a_kn получается из незашифрованного операнда a_n посредством операции «исключающее ИЛИ» с ключом k_n. Для простоты то же самое предполагается для операнда b_kn.Таким образом, b_kn эквивалентно результату операции «исключающее ИЛИ» над незашифрованным операндом b_n с ключом k_n. В вышеприведенном примере, спецификация вычисления над открытым текстом имеет вид: a И b. Спецификация вычисления над шифрованным текстом, которая получается в результате нескольких математических подопераций и в соответствии с которой реализуется блок шифрования, вытекает следующим образом из первой строки уравнения (5):

(5a)

Незашифрованные операнды a_n и b_n были заменены в уравнении (5) математической комбинацией зашифрованного операнда a_kn и ключа k_n и b_kn и ключа k_n, соответственно, и эта математическая комбинация является обратной алгоритму шифрования. Таким образом, в правой части уравнения (5а) представлена спецификация вычисления над шифрованным текстом, полученная непосредственно из спецификации вычисления над открытым текстом.

Если операция «исключающее ИЛИ» используется в качестве алгоритма шифрования, то обратной функцией алгоритма шифрования вновь является функция «исключающее ИЛИ», т.е. она идентична алгоритму шифрования.

Для получения фактической реализации нужно иметь возможность преобразования спецификации вычисления над шифрованным текстом правой части уравнения (5а), где теперь присутствуют только зашифрованные операнды и ключи, любым описанным способом. Это преобразование может быть обеспечено соответствующими математическими законами и т.д. и представлено здесь для случая шифрования посредством «исключающего ИЛИ» или «исключающего НЕ-ИЛИ».

Предпочтительно использовать последнюю строку уравнения (5), полученную из правой части уравнения (5а), когда выполняется совокупность математических преобразований, как основание для реализации обрабатывающего устройства (10 на фиг.1). Таким образом, из уравнения (5а) можно видеть, как спецификация открытого текста для операции с незашифрованными операндами (a_n×b_n) преобразуется в спецификацию вычисления над шифрованным текстом с математическими подоперациями путем замены незашифрованных операндов комбинацией зашифрованных операндов и параметров шифрования, причем эти математические подоперации можно реализовать любым способом, необходимым для математических преобразований, а именно, в соответствии с предварительным условием, согласно которому никакие подоперации не должны содержать в качестве входной величины операнда в виде открытого текста, для которого существует зашифрованный операнд.

Если шифруется только один операнд, то предварительное условие состоит в том, что операнд в виде открытого текста, соответствующий зашифрованному операнду, нельзя использовать нигде в качестве входной величины для математической подоперации.

На фиг.4а показана реализация операции ИЛИ над двумя операндами «а» и «b».

(6)

Уравнение (6) также указывает путь, которым можно следовать, чтобы получить совокупность подопераций, начиная с операции, использующей незашифрованные операнды, и с последующим шифрованием, причем совокупность подопераций такова, что они теперь содержат только зашифрованные операнды и параметр шифрования. На фиг.4а показано, как схемотехническая реализация канонической дизъюнктивной формы зашифрованной операции ИЛИ, использующая три подоперации И 141, 142, 143, две подоперации ИЛИ 144 и 145, а также операцию 146 отрицания и/или НЕ с ключом k, осуществляется на фиг.3а. Различные промежуточные результаты в уравнении (6) показывают, что АЛУ можно, конечно, реализовать различными способами, в данном случае, например, с использованием инвертирования зашифрованного первого операнда a_k, зашифрованного второго операнда b_k и/или ключа k.

Таблица истинности на фиг.4b показывает правильность схемотехнической реализации АЛУ, показанной на фиг.4а, при сравнении седьмого столбца с восьмым столбцом.

Ниже со ссылкой на фиг.5а описана реализация операции НЕ-ИЛИ над зашифрованными операндами. Для этого рассмотрим следующее уравнение (7).

(7)

На фиг.5а показана схемотехническая реализация уравнения (7). В качестве арифметических подопераций используются операции И 151-153, операции ИЛИ 154, 155 и операции НЕ 156 и 157, взаимодействующие и связанные друг с другом, согласно показанному на фиг.5а. Следует еще раз указать, что на фиг.5