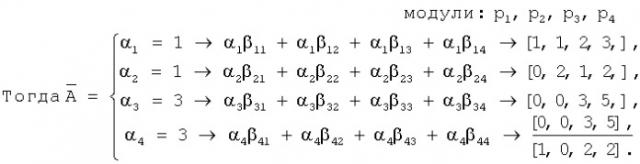Адаптивная параллельно-конвейерная нейронная сеть для коррекции ошибок

Адаптивная параллельно-конвейерная нейронная сеть для коррекции ошибок

Иллюстрации

Показать все

Реферат

Изобретение относится к области вычислительной техники и может быть использовано для построения модулярных нейрокомпьютеров.

Известно устройство для контроля и исправления ошибок в избыточном модулярном коде (патент №2022472, RU 5 Н 03 М 13/00), содержащее блоки сравнения, блоки умножения, блоки элементов «ИЛИ», блоки элементов «И», блоки преобразователей и вычислителей.

Недостатками устройства являются сложность аппаратной реализации и низкое быстродействие.

Наиболее близким к данному изобретению является устройство для обнаружения ошибок в информации, представленной в системе остаточных классов (патент №2022471, RU 5 Н 03 М 13/00), которое содержит блок преобразования СОК-ОПС, блок вычисления индекса числа, блок вычисления дополнительного кода индекса, сумматора, блок вычисления антииндекса суммы, блок сравнения, блок умножения на константу, счетчик.

Однако это устройство используется только при одном основании, что резко снижает его работоспособность в случае появления одновременно ошибок по двум основаниям.

Цель данного изобретения - уменьшить аппаратурную сложность, расширить функциональные возможности и повысить скорость коррекции ошибок. Это достигается тем, что в устройство введен блок обнаружения ошибки, блок реконфигурации и локализации ошибки и блок исправления ошибки.

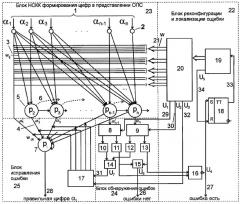
На чертеже представлена схема предложенного устройства, которое содержит блок нейронной сети конечного кольца (НСКК) формирования цифр в представлении ОПС - 23, блок обнаружения ошибок - 26, блок реконфигурации и локализации ошибки - 22, блок исправления ошибки - 25.

Стандартная система счисления избыточных чисел характеризуется рядом k-парных простых чисел {р₁,р₂...p_n}, где (p_i,p_j)=1 для i≠j. Рассмотрим комплексно вопросы обнаружения, локализации и исправления ошибок в модулярных вычислительных структурах и их реализацию на основе использования нейронных сетей.

Известно, что система со смешанным основанием, иногда называется обобщенной позиционной системой счисления (ОПС), используется для реализации алгоритмов нахождения позиционных характеристик непозиционного представления чисел. Как будет показано ниже, коэффициенты системы счисления со смешанным основанием могут быть использованы для определения ошибки, ее локализации, а также для исправления ошибки. Проблема состоит только в том, что необходимо найти методы и алгоритмы быстрого нахождения коэффициентов этой системы.

Целое число А∈[0,Р-1], где Р=р₁·р₂·...p_n может быть представлено в виде следующего выражения

где a_i - коэффициенты ОПС; р_i - основания системы счисления, для i=[1,n].

Как видно из выражения (1), система со смешанным основанием представляет собой позиционную систему счисления, поэтому коэффициенты в представлении со смешанными основаниями могут быть использованы для определения знака, сравнения абсолютных величин, определения переполнения и др., в то время как числа, представленные в остатках, являющиеся непозиционными, не могут этого делать. Известен итеративный алгоритм преобразования цифр из остаточного представления в представление со смешанным основанием, который может быть осуществлен в магистральном (потоковом) варианте. Основным недостатком этого алгоритма является большое время преобразования, которое определяется (n-1) циклами синхронизации. Для ускорения преобразования данных, представленных в СОК, в представлении обобщенной позиционной системы предлагается следующий способ.

Пусть α₁, α₂...α_n представляет собой целые числа в системе остаточных классов по модулю р_i, тогда:

где А≤Р-1; A_i≤Р-1 для i=1,2,...n.

Выражение (2) числа А представляет собой набор i-х ортогональных проекций числа А.

Представим А_i в обобщенной позиционной системе счисления

A_i=a_ijq_i+a_ij+1q_i+1+...+a_inq_n, где и q₁=1.

Из выражений (2) и (3) видно, что оба представления числа А_i в остаточных цифрах и в обобщенной позиционной системе имеет (i-1) нулей перед первым значащим элементом (α_i и α_ij). Этот факт имеет место по определению вследствие того, что α_i по модулю р_j равно нулю (для j<i). Поэтому любая цифра в представлении обобщенной позиционной системы счисления весомозначная по q_k для k<i приведена к нулевому значению. На основании (2) и (3) число А может быть записано в виде суммы остаточных представлений А_i(i=1,2,...n) по модулю Р

Цифры суммы A_i могут быть получены из цифр a_i в представлении обобщенной системы счисления

где а_i<р_i и , поскольку представление в обобщенной позиционной системе счисления числа в области [0,P-1] единственное. Отсюда следует, что а_i является цифрой в представлении обобщенной позиционной системе счисления.

Из выражений (4) и (5) можно записать

где В_i - ортогональные базисы (i=1,2,...n);

- цифры СОК;

b_ij - ортогональные базисы, представленные в обобщенной позиционной системе, для i=1,2...n.

На основании (6) запишем выражение для

где а_i - коэффициенты ОПС;

α_i - разрядные цифры СОК;

b_ij - ортогональные базисы в ОПС.

Цифры а_i в представлении ОПС получаются суммированием по модулю р_i всех произведений α_ib_ij и переносом, генерируемым при формировании а_i-1. Перенос генерируется как число раз, когда сумма цифр в ОПС переполняется по модулю р_i. Этот процесс используется для формирования цифр а_i+1. Последний перенос m, генерируемый при получении последней цифры числа в ОПС a_i, представляет собой абсолютную величину m·p₁p₂...p_n или mP, и поэтому он отбрасывается.

Рассмотренный метод может быть выполнен в параллельном режиме за два цикла синхронизации. Выигрыш в быстродействии данного метода с итеративным методом очевиден, поскольку уменьшает время преобразования с (n-1) циклов до двух циклов. Цифры α_i могут принимать значения от 0 до р_i-1, a b_ij являются константами, поэтому произведения α_ib_ij можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений α_ib_ij являются остаточные цифры α_i. Для иллюстрации этого алгоритма приведем пример 1.

Пусть р_i={2,3,5,7}, P=2·3·5·7=210, B₁=105, В₂=70, В₃=126, В₄=120.

Тогда из выражения (1,7) определим b_ij:

b₁₁=1, b₁₂=1, b₁₃=2, b₁₄=3;

b₂₁=0, b₂₂=2, b₂₃=1, b₂₄=2;

b₃₁=0, b₃₂=0, b₃₃=1, b₃₄=4;

b₄₁=0, b₄₂=0, b₄₃=0, b₄₄=4.

Пусть А=3=(1,0,3,3) представлено в СОК, тогда в ПЗУ поместим следующие числа:

α₁b₁₁=1, α₁b₁₂=1, α₁b₁₃=2, α₁b₁₄=3;

α₂b₂₁=0, α₂b₂₂=0, α₂b₂₃=0, α₂b₂₄=0;

α₃b₃₁=0, α₃b₃₂=0, α₃b₃₃=3, α₃b₃₄=5;

α₄b₄₁=0, α₄b₄₂=0, α₄b₄₃=0, α₄b₄₄=5.

Применительно к нейронным сетям, эти произведения будут образованы путем умножения входных сигналов на весовые коэффициенты.

Преобразование числа показано ниже. Здесь показана реализация с использованием ПЗУ. При нейросетевой реализации данного алгоритма роль ПЗУ выполняют Синаптические веса нейронов.

Проверим результат оценки величины А с помощью метода ортогональных базисов и метода обобщенной позиционной системы счисления (1, 6):

А=α₁В₁+α₂B₂+...+α_nB_n(modP)=1·105+0·70+3·126+3·120(mod210)=

=105+0+378+360(mod210)=843mod210=3

A=a₁+a₂p₁+a₃p₁p₂+a₄p₁p₂p₃=a₁+a₂2+a₃6+a₄30=1+2+0+0=3.

Из примера видно, что алгоритмы обоих методов дают одно и то же позиционное число, которое равно исходному числу А=3.

Рассмотренный метод может быть выполнен в параллельном режиме, что и позволяет провести высокоскоростное преобразование числа от остаточного представления к представлению со смешанным основанием.

Для определения ошибки или переполнения машинного диапазона чисел, а также для их устранения используются избыточные СОК, имеющие n рабочих и r контрольных оснований. Известно, что для практического применения достаточно иметь два избыточных основания, т.е. r=2, тогда система гарантировано обнаруживает появление одновременно двух ошибок и одну ошибку исправляет. Если в числе А=(а₁,а₂...а_n,а_n+1,а_n+2) избыточные цифры а_n+1=а_n+2=0, тогда это число безошибочное. Аналогично определяем и переполнение диапазона представимых чисел. Если в примере 1, приведенном выше, принять в качестве рабочих оснований р₁ и р₂, а в качестве избыточных - р₃ и р₄, то видно, что в данном случае переполнения машинного диапазона и ошибок в числе нет, так как цифры избыточных оснований а₃=а₄=0.

Таким образом, для определения ошибки и переполнения необходимо сравнить избыточные цифры ОПС с нулем.

Теперь рассмотрим метод локализации ошибки.

Ошибка происходит в том случае, когда правильное число А, представленное n+r остаточными цифрами А=(α₁,α₂...α_i...α_n+r), меняется на другое число , если ошибка произошла в i-й остаточной цифре, то неправильное число переходит в запрещенный интервал. Задача состоит в определении модуля ИСОК, ошибка по которому привела к такой ситуации.

Для определения места ошибки используется метод проекций. Проекция р_i обозначается как A=(α₁,α₂...α_i-1,α_i+1...α_n+r), т.e. А представлено в сокращенной (усеченной) ИСОК при исключении i-й остаточной цифры. Поскольку ИСОК является невзвешенной системой, исходная информация сохраняется, когда эта избыточность изменяется. Каждая p_i-проекция может рассматриваться как представление А в определенном пространстве первоначальной системы. Следовательно, если в ИСОК при r≥2 окажется такая ситуация, что для любого произвольного числа А одна из проекций числа А_i будет правильной для любого i=1,...,(n+r), тогда все другие проекции Х_j при j≠1 являются неправильньми и остаточная цифра α_i определяется как ошибочная. В этом состоит суть метода локализации ошибки.

Правильность проекции можно определить из соответствующих цифр числа в ОПС, равных нулю. Таким образом, локализация ошибки может быть решена путем вычисления цифр ОПС для (n+r) проекций и определения, которые из избыточных цифр ОПС нулевые.

Проекция в ОПС представляется выражением

где 0≤а_i<р_i; i=1,2...(n+r), а произведение считается равным 1.

Если ограничение k≠j передвигать при расчете А_n+r, тогда представление ОПС определяется на полное пространство ИСОК и первые коэффициенты А_n+r-1 определяют проекцию А_n+r. Это свойство характеризует математический принцип, который позволяет вычислять цифры со смешанным основанием для всех проекций, при этом если j-я остаточная цифра а_j ошибочная, то проекция А_j не содержит ошибки, потому что а_j отброшена. Определить ошибочную остаточную цифру и заменить ее на правильную цифру а_j≡A_jmodp_j возможно последовательным формированием элементов а_j для каждой проекции и проверкой а_j на равенство нулю. Таким образом, для исправления ошибок необходимо, прежде всего, определить номера оснований, которым соответствуют искаженные символы.

Рассмотрим принцип исправления ошибок.

После определения основания, по которому произошла ошибка, необходимо найти коэффициенты ОПС, а затем по найденным коэффициентам определить цифры a_i, представленные в СОК по основаниям р₁, р₂...p_n.

В ОПС число представляется выражением (1). Найдем его представление в СОК. Пусть известно представление числа А в ОПС.

A=[a₁,a₂...a_n]

Так как основания в СОК постоянны, то представление чисел Q₁=1, Q₂=p₁, Q₃=p₁p₂,...Q_n=p₁p₂...p_n можно заранее вычислить в ОПС:

Тогда из выражения (1) следует, что цифры α₁, α₂...α_n можно найти из сравнений:

Если в системе (11) числа а₁, а₂...а_n считать известными, то решение этой системы дает значения α₁, α₂...α_n.

Пример 2. Перевести число А=[1,1,0,0], представленное в ОПС, в СОК по основаниям р₁=2, р₂=3, р₃=5, р₄=7.

Представим числа Q₁, Q₂...Q_n в СОК:

Q₁=1=(1,1,1,1);

Q₂=2=(0,2,2,2);

Q₃=6=(0,0,1,6);

Q₄=30=(0,0,0,2);

На основании выражения (11) запишем

А=(1,1+1·2,1+1·2+0·1,1+1·2+0·6+0·2=(1,0,3,3).

Таким образом, число А=[1,1,0,0], представленное в ОПС, выглядит как число (1,0,3,3), представленное в СОК по основаниям р₁=2, р₂=3, р₃=5, р₄=7.

Конечный процесс обнаружения, локализации и исправления ошибки может быть представлен в виде обобщенного алгоритма:

1. Вычисление цифр ОПС. Если А правильное, тогда ошибки нет, если А

неправильное - есть ошибка и тогда перейдем к шагу 2.

2. Вычисление цифр ОПС проекций числа А, если проекция А_j, где j=1,2,...(n+r), неправильная, то в разряде j нет ошибки, если проекция правильная, то в данном разряде есть ошибка и тогда перейдем к шагу 3.

3. Вычисление чисел СОК α_j согласно выражению (11) и переход к шагу 4.

4. В исходном числе А, представленном в СОК, заменяем цифру α_j. На этом процесс корректирования ошибки заканчивается.

Приведенный алгоритм может быть реализован на основе применения нейронных сетей конечного кольца.

Числовая иллюстрация.

Принципы обнаружения, локализации и исправления ошибок в избыточной СОК могут быть продемонстрированы с помощью числового примера. Предположим, необходимо реализовать функциональный блок модулярного нейрокомпьютера для коррекции ошибок. Пусть набор модулей р_i, на которых основаны каналы модулярного нейрокомпьютера такой же, как и в примере 1. Выберем модули р₁=2, р₂=3 рабочими, а p₃=5, p₄=7 - контрольными, тогда полный диапазон будет равен Р=210, а рабочий Р=2·3=6. Допустим, правильный результат равен а=(1,0,3,3), а искаженный . Для определения ошибки вычислим коэффициент ОПС а_i.

Таким образом, число в ОПС равно [1,0,2,2]. Из выражения (1) видно, что вышло за пределы рабочего диапазона, так как 73>6. Для принятия решения о том, что число искаженное, необходимо проверить на равенство нулю коэффициенты а₃ и а₄. Итак, неравенства а₃≠0 и а₄≠0 устанавливают тот факт, что число - ошибочное. Вычислим проекции числа , полученные из последовательным зачеркиванием цифр α_i по основанию р_i.

По основанию p₁=2.

Для системы с основаниями р₂=3, р₃=5, р₄=7 вычислим ортогональные базисы в позиционной и обобщенной позиционной системах счисления :

и

Этот результат может быть проверен оценкой величины с помощью выражения (1) .

По основанию р₂=3.

Для системы с основаниями p₁=2, р₃=5, p₄=7 вычислим ортогональные базисы в позиционной и обобщенной позиционной системах счисления :

и

.

По основанию р₃=5.

Для системы с основаниями р₁=2, р₂=3, р₄=7 вычислим ортогональные базисы в позиционной и обобщенной позиционной системах счисления :

и

.

По основанию p₄=7.

Для системы с основаниями p₁=2, р₂=3, р₃=5 вычислим ортогональные базисы в позиционной и обобщенной позиционной системах счисления :

и

.

Итак, все проекции числа , кроме , неправильны. Следовательно, ошибочной цифрой является цифра α₂=1 по основанию р₂=3.

Проведем теперь исправление по формуле (7) для проекции

α₂=(1+1·2)mod3=0mod3.

Правильная цифра по основанию р₂=3 равна α₂=0.

Этот пример был приведен для иллюстрации принципа реализации функционального блока коррекции ошибки в модулярном нейрокомпьютере. Эффективность вычислений модулярного нейрокомпьютера повышается, так как возможность такого режима обработки информации эквивалентна двойному просчету для обнаружения ошибки и тройному просчету для ее исправления. Модулярный нейрокомпьютер с двумя контрольными основаниями позволяет сохранить работоспособность нейрокомпьютера при отказах любых двух каналов, при этом он выполняет программу при некотором уменьшении точности или скорости вычислений, т.е. нейрокомпьютер, работающий в модулярной арифметике, является исключительно «живучим», приближаясь в этом смысле к биологическим системам.

Рассмотрим адаптивную параллельно-конвейерную нейронную сеть коррекции ошибок, которая представляет собой высокопроизводительное нейросетевое устройство и предназначено для параллельно-конвейерной коррекции ошибок. Схема приведена на чертеже. Рассмотрим основные функции структурных блоков адаптивной нейронной системы. Пунктиром обведены основные блоки, реализуемые в нейросетевом базисе.

Блок нейронных сетей конечного кольца (НСКК) 23 вычисляет разрядные цифры в представлении ОПС и состоит из (n-1) НСКК, нейроны 5 с переносами 6 и нейроны входного слоя 2. Из чертежа видно, что остаточные числа α_i(i=1,2,...n) контролируемого числа A=(α₁,α₂,...,α_n) 1 подаются параллельно через входной слой, нейроны 2, на входы всех НСКК, нейроны 5, которые имеют n(n+1)/2 синаптических весов. Подключения синаптических весов на чертеже показаны точками. Полученная треугольная матрица (12) суммируется согласно правилу сложения цифр в представлении ОПС, описанному выше, т.е. данные в i-м канале будут суммироваться с учетом переносов в (i-1) канале по модулю р_i в представлении ОПС. Перенос представляет собой число раз, превышающее величину модуля p_i, который поступает к (i+1) каналу. Поскольку в каждой строке имеется (i-1) нулей перед первым значащим элементом, а сумма чисел может переноситься (n-1) раз, то абсолютная величина каждого переноса ограничивается величиной (n-1)

где w_ij=b_ij.

Для обнаружения ошибки используется первоначальная конфигурация блока, т.е. такая конфигурация, когда работают все каналы. При формировании i проекций, когда происходит реконфигурация сети, возникают две задачи: первая задача связана с исключением i-канала, нейроны 5, а вторая - с коррекцией весовых коэффициентов w_ij сигналы w 21. Структура нейронной сети i-проекции зависит от номера исключаемого канала и адаптируется к нему посредством загрузки весовых коэффициентов w_ij 3. В то время, когда часть сети остается неактивной (исключается из системы), весовые коэффициенты между нейронами входного слоя и нейронами скрытого слоя НСКК не используются нейронной сетью и равны нулю. Весовые коэффициенты между нейронами скрытого слоя и нейронами выходного слоя НСКК не активированных нейронов также равны нулю, а нейроны выходного слоя не активированной части нейронной сети имеют высокое значение (преимущественно ∞), т.е. можно считать, что они исключаются из общей системы.

Посредством коммутации весовых коэффициентов нейронная сеть осуществляет реконфигурацию системы и ее настройку в соответствии с изменением констант СОК. Определенные активированные части нейронной сети активируют другие части, при этом весовые коэффициенты определены из новых констант СОК. В процессе реконфигурации активные нейроны целенаправленно активируют определенные части нейронной сети, просто и быстро приспосабливаясь к определенным внешним параметрам. Таким образом, в процессе вычисления проекции весовые коэффициенты активированной части нейронной сети адаптируются к требованиям внешних параметров. Исходя из этого, вычисление проекций нейронной сетью не содержит каких-либо сложных условий реконфигураций системы и вследствие этого происходит быстрое определение значений величины проекций.

Функционирование нейронной сети зависит от весовых коэффициентов между слоями 22, которые определяются заранее и хранятся в памяти блока реконфигурации и локализации ошибки.

Процесс вычисления проекций осуществляется активизацией определенных выходов НСКК, которые выбраны с помощью весовых коэффициентов. Таким образом, реконфигурация сети осуществляется весовыми коэффициентами нейронных связей на активированных выходах нейронной сети.

Весовые коэффициенты определяются заранее и помещаются в памяти блока реконфигурации, и в зависимости от поступающих сигналов выдаются необходимые весовые коэффициенты для i-проекции, соответственно, определяя структуру нейронной сети, в которой при определенных внешних параметрах достигается надежное и быстрое вычисление проекций числа.

Блок обнаружения ошибок 24 предназначен для сравнения значений избыточных разрядов всего числа или его проекций с нулем и состоит из четырех схем сравнений (СС1-СС4(10-13)), элементов «И» 15, «ИЛИ» 14 и двух демультиплексоров (ДМХ1 8, ДМХ2 9). Если какая-либо из избыточных цифр в представлении ОПС не равна нулю, то в исходном числе присутствует ошибка. Схемы сравнения СС2 11 и СС4 13 предназначены для сравнения избыточных цифр всего числа с нулем. Если а_n-1 и а_n равны нулю, то схемы сравнения выдают единичные сигналы, которые поступают на вход элемента «И» 15, на выходе которого формируется сигнал «ошибки нет». Выходной сигнал U₆ элемента «И» 15 классифицируется как сигнал «ошибки нет» 26. Во всех остальных случаях сигналы сравнения СС2 11 и СС4 13 с помощью схемы И-НЕ 16 классифицируются как сигнал U₄ «ошибка есть» 27, который поступает на вход S-триггера 18 блока реконфигурации и локализации ошибок 22. Необходимо отметить, что при вычислении проекций числа от 1 до (n-1), в качестве избыточной цифры используется коэффициент а_n, а при вычислении n-й проекции - коэффициент a_n-1 . Это обстоятельство связано с тем фактом, что при определении проекции числа, когда одно основание исключается, избыточный код с двумя контрольными основаниями превращается в избыточный код с одним контрольным основанием, его корректирующая способность уменьшается, он из исправляющего кода превращается в обнаруживающий код, но этого достаточно для обнаружения неправильной проекции, хотя при этом исправляющие свойства кода теряются. В случае если в исходном числе есть ошибка, то на адресные входы демультиплексоров ДМХ1 8 и ДМХ2 9 поступают соответственно сигналы U₁ 29 и U₂ 30. Сигнал U₁ 29 блокирует выходы демультиплексора ДМХ1 8 при определении (n-1) проекций, а сигнал U₂ 30 коммутирует вход демультиплексора ДМХ2 9 на вход схемы сравнения ССЗ 12. Если при контроле проекции a_n=0, то схема сравнения ССЗ 12 формирует единичный сигнал правильной проекции, что соответствует ошибке по данному основанию, который поступает на вход элемента «ИЛИ» 14. Элемент «ИЛИ» 14 классифицирует сигнал U₇ 31 как «ошибочный разряд», который поступает на вход блока исправления ошибки 25. Процесс вычисления коэффициента a_n будет выполняться (n-1) раз. При определении n-й проекции формируются новые коды символов U₁ и U₂, которые блокируют выход демультиплексора ДМХ2 9, а выход демультиплексора ДМХ1 8 коммутируется на вход схемы сравнения СС1 10, при этом избыточный коэффициент а_n-1 будет выполнять роль избыточного коэффициента а_n. Если в данном случае а_n-1=0, то схема СС1 10 выполняет роль схемы СС3 12 и процесс происходит аналогично тому, как и при a_n=0.

Блок исправления ошибок 25 служит для исправления ошибок по i-основанию и состоит из адаптируемой нейронной сети конечного кольца, нейроны 7, и ПЗУ весовых коэффициентов 17. Адаптируемая нейронная сеть конечного кольца имеет максимально необходимую конфигурацию, которая обеспечивает вычисление правильной разрядной цифры по любому основанию, используемому в выбранной СОК. Нейронная сеть реализует вычислительную модель (11). Структура адаптируемой нейронной сети зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w_jk (где k=1,2...n) 4, которые определяются q_i. Вычисление правильной цифры α_i определяется изменением весовых коэффициентов между нейронами входного слоя и нейронами скрытого слоя и связями между нейронами скрытого слоя и нейронами выходного слоя. В зависимости от числа входов и их весовых коэффициентов изменяется модуль СОК реализуемой нейронной сети конечного кольца. Для управления конфигурацией нейронной сети используется ПЗУ весовых коэффициентов 17, которая управляется сигналами U₇ 31 «ошибочная цифра» и сигналом U₃ - номер проекции 32, соответственно, поступающими от блока обнаружения 24 и блока реконфигурации и локализации ошибок 22. Объем ПЗУ в битах можно определить из выражения

Блок реконфигурации и локализации ошибки 22 предназначен для управления адресными входами демультиплексоров ДМХ1 8 и ДМХ2 9 соответственно, сигналы U₁ 29 и U₂ 30 управления конфигурацией блока НСКК 23 и коррекцией весовых коэффициентов деградированной нейронной сети 23, сигнал w 21, и формирования сигнала U₃ номера проекции. Блок состоит из ПЗУ формирования проекции и коррекции весовых коэффициентов 20, счетчика проекций 19, триггера управления 18, обеспечивающего работу счетчика на время формирования всех проекций и элемента И-НЕ 16, формирующего сигнал U₄ 27 установки триггера в единичное состояние, в случае обнаружения ошибки в проверяемой кодовой комбинации. В случае, если один или оба разряда а_n и a_n-1 не равны нулю, элемент И-НЕ 16 формирует сигнал U₄ 27 «ошибка есть», который поступает на вход S-триггера 18 и переводит его в состояние «1». Высокий потенциал - сигнал 33 на выходе триггера запускает счетчик проекций 18. В каждом такте синхронизации счетчик проекций активирует ПЗУ формирования проекций и коррекции весовых коэффициентов 20, которое формирует сигналы: формирования первой проекции и коррекции весовых коэффициентов, сигналы w 21; формирования адресной части демультиплексоров (ДМХ1 8 и ДМХ2 9), сигналы U₁ 29 и U₂ 30, и номера проекции, сигнал U₃ 32. Объем ПЗУ составляет , где b_i - двоичное представление i-цифры СОК. По сигналу U₁ 29 блокируется ДМХ1 8, а по сигналу U₂ 30 выход ДМХ2 9 подключается к схеме сравнения ССЗ 12.

Формируемые ПЗУ 20 весовые коэффициенты w 21 осуществляют реконфигурацию нейронной сети и адаптируют каждую НСКК к новым входным параметрам. Сигналы адресной части 30 демультиплексора ДМХ2 9 коммутируют старший разряд а_n ко входам схемы сравнения ССЗ 12, которая формирует сигнал U₇ 31 управления ПЗУ весовых коэффициентов блока исправления ошибки 17, если а_n=0. На вход этого блока поступает и сигнал номера проекции U₃ 32. По этим сигналам w 21 адаптируемая НСКК 23, нейроны 5, настраивается на первую проекцию. После вычисления данных первой проекции, счетчик проекций 19 формирует сигналы второй проекции и процесс повторяется аналогичным образом до получения (n-1) проекций. Далее сигнал U₂ 30 блокирует выходы демультиплексора ДМХ2 9, а сигнал U₁ 29 коммутирует выход демультиплексора ДМХ2 9 на вход схемы сравнения СС1 10, которая, в случае a_n-1=0, формирует единичный сигнал, поступающий через элемент «ИЛИ» 14 на вход ПЗУ коэффициентов в качестве сигнала U₇ 31. После того как все проекции будут вычислены, счетчик проекции подает сигнал U₅ 34 на вход R-триггера, который переходит в нулевое состояние и выключает активацию счетчика, а также формирует сигналы установки в начальное состояние демультиплексоров и ПЗУ весовых коэффициентов блока исправления ошибок. После этого нейронная сеть коррекции ошибок переходит в исходное состояние и способна принимать следующую кодовую комбинацию для коррекции числа.

Итак, обнаружение, локализация и исправление ошибки могут быть выполнены в параллельно-конвейерном режиме, что и показано на рисунке 1 за (n+2) циклов синхронизации: 2 цикла - для обнаружения ошибки, (n-1) циклов - для локализации ошибки и 1 цикл - для исправления ошибки.

Принцип работы данного изобретения излагается ниже.

Изобретением является адаптивная нейронная сеть для коррекции ошибок в кодах данных 1. Данные поступают на вход нейронов 2, а исправленная цифра 28 появляется в выходном слое адаптивной нейронной сети 7 блока 25.

Из чертежа видно, что контролируемое число А=(α₁,α₂,...α_n) подается параллельно на вход 1 блока НСКК 23 формирования цифр в представлении ОПС, на выходе которого в 1-м цикле синхронизации вычисляются разрядные цифры числа А=[a₁ ⁰,a₂ ⁰,...a⁰ _n-1,a_n ⁰], представленные в ОПС, где индекс «0» соответствует коэффициентам ОПС исходного числа. Адаптивная НСКК 25 блока исправления ошибки в этот момент не активна. Избыточные цифры а⁰ _n и а⁰ _n-1 через демультиплексоры ДМХ2 9 и ДМХ1 8 поступают на вход схем сравнения СС2 11 и СС4 13 блока обнаружения ошибки 24. Если a⁰ _n-1=a⁰ _n=0, то элементом «И» 15 формируется сигнал отсутствия ошибки «ошибки нет» 26, на этом контроль числа заканчивается. Если же одна или обе из избыточных цифр а⁰ _n и а⁰ _n-1 не равны нулю, элемент И-НЕ 16 фиксирует сигнал U₄ «ошибка есть» 27, который посредством триггера 18 и счетчика проекций 19 активизирует ПЗУ формирования проекции и коррекции весовых коэффициентов 20, которое в свою очередь активизирует блок НСКК 23 сигналы w 21 формирования цифр в представлении ОПС на вычисление проекций числа, переключения демультиплексора ДМХ2 9 (под действием сигнала U₂ 30) на вход схемы сравнения ССЗ 12, а также формирует сигнал номера первой проекции U₃ 32, который поступает на вход ПЗУ весовых коэффициентов 17 блока исправления ошибок 25.

Если аⁱ _n≠0, где i=1,2...,n - номер проекции, то данная проекция неправильная и поэтому ошибка по этому основанию отсутствует, и схема на эту ситуацию никак не реагирует. Если aⁱ _n=0, то данная проекция правильная, что свидетельствует о наличии ошибки по данному основанию р_i. Сформированные схемами СС1 10 и ССЗ 12 сигналы через элемент «ИЛИ» 14 поступают на вход ПЗУ весовых коэффициентов 17 блока исправления ошибок 25. Под действием двух входных сигналов ПЗУ весовых коэффициентов 17 активируется, происходит адаптация НСКК 25, нейроны 7, по модулю р_i и определяется правильная цифра 28 по основанию p_i. После вычисления первой проекции счетчик проекций выдает сигнал на вычисление следующей проекции и процесс повторяется до тех пор, пока счетчик не выдаст сигнал на формирование (n-1)-проекции, при этом демультиплексор ДМХ2 9 блокируется, а выход демультиплексора ДМХ1 8 подключается к схеме сравнения СС 10 и процесс повторяется аналогично вышеописанному.

Счетчик имеет емкость, равную n. После вычисления n проекций счетчик проекций 19 формирует сигнал окончания контроля U₅ 34, который поступает на вход R-триггера 18, и переводит его в нулевое состояние, по которому система устанавливается в исходное положение.

Выигрыш в быстродействии параллельно-конвейерного обнаружения, локализации и исправления ошибок очевиден, поскольку он значительно уменьшает время по сравнению с известными реализациями. Это преимущество объясняется совершенно параллельным принципом обработки данных и соответствующей организацией нейронных сетей. Так, разработанная адаптивная НСКК позволяет исправить ошибку за (n+2) циклов синхронизации, в то время как известные реализации позволяют выполнить эту операцию как минимум за 3 n циклов синхронизации.

Разработанная адаптивная параллельно-конвейерная нейронная сеть может быть применена в модулярных нейрокомпьютерах для обнаружения, локализации и исправления ошибок, что открывает новые перспективы, которые ранее было очень сложно осуществить. Реализация разработанной системы может быть выполнена на ПЛИС Xilinx серии ХС4000ЕС, для которой время задержек на вентиле составляет не более одной наносекунды и ниже.

Адаптивная параллельно-конвейерная нейронная сеть для коррекции ошибок, содержащая блок нейронной сети конечного кольца формирования цифр в представлении обобщенной позиционной системы, отличающаяся тем, что в нее включены блок обнаружения ошибок, блок исправления ошибок и блок реконфигурации и локализации ошибок, при этом информационный вход адаптивной параллельно-конвейерной нейронной сети соединен с входом блока нейронной сети конечного кольца формирования цифр в представлении обобщенной позиционной системы, при этом блок исправления ошибок содержит первую адаптируемую нейронную сеть конечного ко