Способ и устройство для хранения и восстановления криптографического секретного ключа

Способ и устройство для хранения и восстановления криптографического секретного ключа

Иллюстрации

Показать все

Реферат

1. Область техники

Настоящее изобретение в общем относится к криптографическим системам. В частности, изобретение относится к устройству и способу для хранения и восстановления секретного ключа в криптографической системе с открытым и секретным ключами.

2. Описание известного уровня техники

Одной из распространенных форм шифрования открытым ключом является алгоритм шифрования Ривеста-Шамира-Эдельмана (Rivest, Shamir, Adelman), сокращенно именуемый как RSA-кодирование. В RSA-кодировании используется открытый ключ, состоящий из открытого модуля n и открытого показателя степени е, и секретный ключ, состоящий из модуля n и секретного показателя степени d. Открытый модуль n представляет собой целое число, являющееся произведением двух различных простых множителей р и q, т.е. n=pq. Эти множители являются секретной информацией и не раскрываются владельцем секретного ключа. Открытый показатель степени е представляет собой целое число, которое является простым числом относительно значений (р-1) и (q-1). Секретный показатель степени d является целым числом, так что ed mod(p-1)=ed mod(q-1)=1.

Одним из применений RSA-кодирования является шифрование сообщений. Любое лицо может использовать открытый ключ для шифрования сообщения, которое сможет дешифровать только владелец данного секретного ключа. Пусть m будет сообщением, которое необходимо зашифровать, где m - целое число в интервале 0<m<n. Зашифрованное сообщение с вычисляется как с=m^е mod n. Для декодирования зашифрованного сообщения владелец секретного ключа вычисляет m=c^d mod n. Например, лицо А, желающее послать зашифрованное сообщение лицу В, зашифрует сообщение, получив открытый ключ лица В. Так как данное сообщение можно дешифровать только правильным секретным ключом лица В, который будет связан с его открытым ключом, данное сообщение может быть дешифровано только лицом В.

Другим применением RSA-кодирования является приложение подписи к сообщениям. Владелец секретного ключа может приложить к сообщению подпись, подлинность которой сможет проверить любое лицо, использующее данный открытый ключ. Пусть m будет сообщением, к которому следует приложить подпись, где m - целое число в интервале 0<m<n. Подпись s вычисляется как s=m^d mod n. Для проверки подлинности подписи любое лицо использует открытый ключ для вычисления m'=s^е mod n. Если значение m' совпадает со значением m, значит данная подпись является действительной.

В основе защиты RSA-кодирования лежит предполагаемая сложность определения множителей открытого модуля. Т.е. считается очень трудным определить множители p и q для данного n, чтобы получить n=pq. Сложность проблемы разложения на множители возрастает с увеличением размера р и q. На практике каждый из множителей р и q состоит из сотен или тысяч двоичных чисел (бит), и поскольку n - произведение р и q, оно также состоит из сотен или тысяч бит. Операция модульного возведения в степень, используемая в RSA, является дорогостоящей операцией с точки зрения вычислительных ресурсов. Сложность данной операции возрастает почти линейно с увеличением количества бит в показателе степени и квадратично с увеличением количества бит в модуле. К счастью, существуют некоторые известные методы, позволяющие снизить затраты вычислительных ресурсов.

Чтобы снизить затраты на операцию открытого ключа, принято выбирать малое число для открытого показателя степени. Это приемлемо, поскольку защита RSA-кодирования в основном не зависит от размера открытого показателя степени. Широко распространенным выбором открытого показателя степени является е=2¹⁶+1; это значение, по-видимому, фактически становится стандартом для новых применений. Другими обычными вариантами выбора являются е=3 и е=17. При малом открытом показателе степени затраты вычислительных ресурсов на RSA-операцию открытого ключа относительно невелики. Иными словами, кодирование сообщения или проверка достоверности подписи относительно недороги.

К сожалению, секретный показатель степени d нельзя брать малым. Его значение нельзя выбирать свободно, оно должно удовлетворять условию ed mod(p-1)=ed mod(q-1)=1. Защита RSA-кодирования основана на больших, произвольно выбранных p и q. В результате d представляет собой целое число, размер которого сопоставим с размером открытого модуля n. Это требует относительно больших затрат вычислительных ресурсов на операцию секретного ключа. Иными словами, декодирование сообщения или создание подписи обходятся относительно дорого.

Затраты на операцию секретного ключа можно уменьшить, использовав китайскую теорему об остатках (КТО). Для КТО требуется вычислить несколько величин, а именно:

d_p=d mod(p-1);

d_q=d mod(q-1);

v, чтобы pv mod q=1.

Тогда операция секретного ключа y=g^d mod n вычисляется следующим образом:

a=(g mod p)^dp mod p;

b=(g mod q)^dp mod q;

y=a+[(b-a)v mod q]p.

Если затраты на вычисление d_p, d_q и v незначительные, то затраты вычислительных ресурсов на вычисление операции секретного ключа с использованием КТО составят около четверти затрат на операцию секретного ключа без использования КТО. Это значительно уменьшает вычислительные затраты и делает операцию с использованием КТО желательной для многих применений.

К сожалению, затраты на вычисление d_p, d_q и v не всегда незначительные. Поэтому во многих приложениях значения d_p, d_q и v просто предварительно вычисляются и сохраняются вместе с множителями p и q как часть секретного ключа. Приложение, в котором сохраняется набор параметров {p,q,d_p,d_q,v}, может выполнять операцию секретного ключа с использованием КТО с наименьшими возможными затратами вычислительных ресурсов. Каждый из этих пяти параметров требует b бит памяти, где b - число бит в простом множителе модуля. Следовательно, общий объем памяти для секретного ключа составит 5b бит.

Однако в некоторых приложениях сохранение секретного ключа как {p,q,d_p,d_q,v} нежелательно из-за требующегося для этого объема памяти. Если вместо этого в данном приложении сохранить секретный ключ как {p,q}, то объем памяти для секретного ключа уменьшится от 5b бит до 2b бит, т.е. в 2,5 раза. Однако в данном приложении впоследствии потребуется вычислять d_p, d_q и v каждый раз при выполнении операции секретного ключа. Такие затраты вычислительных ресурсов могут быть нежелательными.

Примером приложения, для которого данные вопросы составляют проблему, является дешевая микропроцессорная карточка (смарт-карта), используемая для создания цифровых подписей. На этой карточке хранится набор секретных ключей RSA, каждый из которых используется для создания подписей для различных целей. Например, один ключ может использоваться для подписи покупок, совершенных по конкретной кредитной карточке; другой ключ можно использовать для подписи сообщений электронной почты; третий ключ можно использовать для подписи банковских сделок и т.д. В силу своей дешевизны микропроцессорная карточка имеет ограниченный объем памяти. Желательно, чтобы карточка могла хранить как можно больше секретных ключей в ограниченном объеме памяти. Более того, из-за своей дешевизны, микропроцессорная карточка имеет простой процессор с ограниченными вычислительными возможностями. Поскольку нежелательно, чтобы вычисление подписи занимало чрезмерное время, важно минимизировать вычислительные затраты на операцию секретного ключа RSA.

Другой проблемой, связанной с вычислением d_p, d_q и v, является защита. Обычным путем вычисления d_p, d_q и v из p и q является использование алгоритма Евклида или его известных вариантов. Алгоритм Евклида - это последовательность арифметических операций, которые можно использовать для решения проблемы "При данных х и z найти y, чтобы xy mod z=1''. Последовательность операций зависит от числовых значений операндов, т.е. изменение числовых значений y или z может вызвать изменение порядка арифметических операций, таких как умножение, вычитание и т.п. Эта зависимость может привести к тому, что хранение секретного ключа в приложении станет уязвимым для раскрытия злоумышленником, способным подобрать вводы данных в приложение, измеряя при этом доступные извне отклики, такие как потребление электрического тока, электромагнитные излучения и т.п. Такие попытки взлома могут успешно выполняться на реальных устройствах защиты как коммерческих, так и государственных. Для снижения уязвимости по отношению к таким попыткам взлома желательно, чтобы последовательность операций, используемых для вычисления d_p, d_q и v, не изменялась с изменением значений p и q.

В рассматриваемом примере дешевой микропроцессорной карточки эта карточка содержит арифметический сопроцессор, который ускоряет операции модульного возведения в степень, используемые в RSA. Во время операций с использованием секретного ключа модульное возведение в степень уязвимо для попыток взлома описанного выше типа. Для снижения уязвимости к таким попыткам взлома сопроцессор тщательно проектируют, чтобы гарантировать, что его последовательность операций не зависит от значений операндов. Однако, если микропроцессорная карточка также должна вычислять d_p, d_q и v во время RSA-операции с использованием секретного ключа, то вычисление d_p, d_q и v является дополнительным источником потенциальной уязвимости. Для уменьшения этой дополнительной уязвимости в вычислении d_p, d_q и v должна использоваться последовательность операций, которая не зависит от значений p и q. Так как p и q являются простыми числами, v можно вычислить с помощью модульного возведения в степень через операцию v=p^q-2 mod q. Таким образом, микропроцессорная карточка может использовать сопроцессор для вычисления v, не вызывая уязвимости, связанной с вычислением v. Однако d_p и d_q невозможно вычислить с помощью модульного возведения в степень. Следовательно, необходима какая-то схема для вычисления d_p и d_q без повышения уязвимости.

Хотя предыдущее обсуждение было сконцентрировано на приложениях с использованием КТО, оно не охватывает все приложения. В некоторых приложениях операция с использованием секретного ключа выполняется без использования КТО, так как это более простая операция (хотя и более дорогая). В некоторых таких приложениях сохраняют свою важность проблемы, связанные с объемом памяти и защитой.

Самый прямой путь сохранения секретного ключа в приложении без использования КТО - это сохранить параметры {n,d}, где n - открытый модуль, а d - секретный показатель степени. При этом хранение секретного ключа может потребовать 4b бит.

Альтернативно, в приложении без использования КТО секретный ключ можно хранить просто как {p, q}, где p и q - простые множители n. При каждом выполнении операции секретного ключа n и d вычисляются из упомянутых хранимых значений p и q. При таком способе хранения секретный ключ требует 2b бита. В результате обеспечивается экономия в два раза по сравнению с хранением ключа как {n,d}. Вычисление n из p и q выполняется как одна операция умножения, поскольку n=pq. Это операция дешевле, чем модульное возведение в степень, и поскольку это одна операция, она не прибавляет уязвимости раскрытию p и q. Однако, как и для d_p и d_q в случае с использованием КТО, вычисление d из p и q может потребовать существенных затрат вычислительных ресурсов и повысить уязвимость защиты из-за вычислительной последовательности, которая изменяется в зависимости от значений p и q.

Таким образом, в основу настоящего изобретения положена задача обеспечения параметризации секретного ключа RSA для применений с использованием КТО, при которой используется меньший объем памяти, чем для полного набора параметров {p,q,d_p,d_q,v}, и обеспечивается более высокая эффективность вычислений, чем с минимальным набором параметров {p,q}.

Задачей настоящего изобретения также является обеспечить параметризацию секретного ключа RSA для приложений без использования КТО, при которой используется меньший объем памяти, чем для полного набора параметров {n,d}, и обеспечивается более высокая эффективность вычислений, чем с минимальным набором параметров {p,q}.

Задачей настоящего изобретения также является обеспечение такого средства для вычисления параметров d_p и d_q с использованием КТО и параметра d без использования КТО, при котором последовательность вычислений не зависит от значений простых множителей p и q, в целях снижения уязвимости к попыткам взлома защиты, использующих такую зависимость.

Краткое изложение сущности изобретения

Для решения этих и других задач известного уровня техники предложены устройство и способ, обеспечивающие схему хранения и восстановления криптографического секретного ключа, которая позволяет одновременно уменьшить необходимый объем памяти и повысить защиту. В частности, предложенная система обеспечивает средство для извлечения секретного ключа из упомянутых хранимых параметров, не использованное ранее, а также средство для вычисления определенных параметров с одновременным уменьшением уязвимости защиты.

Одним аспектом настоящего изобретения является замена параметров d_p и d_q с использованием КТО и параметра d без использования КТО на меньшие параметры k_p, k_q и k, соответственно. Значения k_p, k_q и k - это значения, которые удовлетворяют следующим зависимостям:

k_p(p-1)mod e=1;

k_q(q-1)mod e=1;

k(p-1)(q-1)mod e=1.

Каждое из значений k_p, k_q и k находится в интервале от 1 до (е-1), включительно. Т.е. каждое значение требует не больше бит, чем число бит, необходимое для хранения открытого показателя степени е. В широко распространенном случае е=2¹⁶+1 каждое из значений k_p, k_q и k может храниться как 16-битное число (k_p-1), (k_q-1) или (k-1), соответственно.

В отличие от этого, каждое из значений d_p и d_q требует b бит памяти, а d требует 2b памяти, где b - число бит в простом множителе p или q. Типичное значение b равно 512, что соответствует открытому модулю, имеющему 1024 бит. В этом типичном случае каждое из значений d_p и d_q требует в 32 раза больший объем памяти, чем k_p и k_q, а d требует в 64 раза больший объем памяти, чем k.

В приложении с использованием КТО, в котором сохраняют k_p и k_q, можно восстанавливать d_p и d посредством следующих вычислений:

d_p=[1+(p-1)(e-k_p)]/e;

d_q=[1+(q-1)(e-k_q)]/e.

В приложении без использования КТО, в котором сохраняют k, можно восстанавливать d посредством следующего вычисления:

d=[1+(p-1)(q-1)(e-k)]/e.

В каждом из этих вычислений "/" представляет деление на целое число; в каждом случае делимое является величиной, кратной делителю, поэтому остатка нет. Доказательство, что эти вычисления дают правильные результаты, будет приведено в конце данного описания.

Вычисления для d_p, d_q и d требуют от приложения выполнения деления на открытый показатель степени е. В некоторых приложениях это деление может представлять собой громоздкую или нежелательную операцию. Кроме того, если приложение применяет деление с использованием обычной длинной последовательности операций деления, то последовательность операций может зависеть от значений p и q, что делает секретный ключ уязвимым для попыток взлома защиты, использующих данную зависимость.

Чтобы исключить необходимость в этом делении, приложение с использованием КТО может восстановить d_p и d_q посредством следующих вычислений:

вычислить u, чтобы ue 2^b=1;

d_p=[1+(p-1)(e-k_p)]u mod 2^b;

d_q=[1+(q-1)(e-k_q)]u mod 2^b.

Приложение без использования КТО может восстанавливать d без использования деления посредством следующего вычисления:

вычислить t, чтобы te mod 2^2b=1;

d=[1+(p-1)(q-1)(e-k)]t mod 2^2b.

Доказательство, что эти вычисления дают правильные результаты, будет приведено в конце настоящего описания.

Если временно проигнорировать вычисление u и t, то станет ясно, что вычисления для восстановления d_p d_q или d не требуют больших вычислительных затрат и не обуславливают уязвимость защиты. Каждое вычисление состоит из двух или трех умножений целых чисел, трех или четырех сложений/вычитаний целых чисел и операции "mod 2^b" или "mod 2^2b". Операции умножения, сложения и вычитания подобны операциям, используемым для реализации модульного возведения в степень. В одном модульном возведении в степень используются тысячи таких операций, так что дополнительные затраты всего на несколько операций можно не принимать в расчет. Операция "mod 2^b" является просто усечением до b бит, а операция "mod 2^2b" является усечением до 2b бит; их можно также не принимать в расчет. Эта последовательность операций не зависит от значений p или q, так что вычисления можно осуществлять без повышения уязвимости к попыткам взлома защиты, основанным на такой зависимости.

Обратившись теперь к вычислению u и t, можно легко заметить, что здесь нет проблемы защиты, поскольку в данном вычислении не используется секретный ключ, и оно не создает возможности для попытки получить секретный ключ, независимо от способа его реализации. Кроме того, данное вычисление не требует больших затрат по следующим причинам.

Во-первых, рассмотрим случай, когда открытый показатель степени е одинаков для всех секретных ключей. В этом случае u или t является фиксированной величиной, поэтому ее можно просто сохранить один раз для всех секретных ключей и извлекать при необходимости. Даже если представляющие интерес секретные ключи имеют разную длину, т.е. значение b изменяется в соответствии с данным секретным ключом, необходимо сохранить всего одно значение для u или t, которое соответствует самому большому значению b. Для значений b, отличных от максимального значения, сохраненное значение можно просто усечь, используя "mod 2^b" для u или "mod 2^2b" для t. В распространенном случае e=2¹⁶+1 даже не требуется сохранять u или t, любое из них можно получить посредством экономичных вычислений:

u=[1+(2³²-2¹⁶)+(2⁶⁴-2⁴⁸)+(2⁹⁶-2⁸⁰)+(2¹²⁸-2¹¹²)+...]mod 2^b;

t=[1+(2³²-2¹⁶)+(2⁶⁴-2⁴⁸)+(2⁹⁶-2⁸⁰)+(2¹²⁸-2¹¹²)+...]mod 2^2b.

Подобные вычисления можно произвести и для других обычных выборов е, например е=3 или е=17.

Во-вторых, рассмотрим общий случай, когда для каждого открытого ключа используется различный произвольный открытый показатель степени е. В этом случае приложение должно вычислить u или t, используя универсальный алгоритм, который вычисляет мультипликативную инверсию числа относительно какого-то модуля, т.е. степень числа 2 (такую как 2^b или 2^2b). Такие алгоритмы хорошо известны и просты в вычислениях. Во многих приложениях такой алгоритм уже применяется как часть операции модульного возведения в степень; в частности, многие приложения, которые используют умножение Монтгомери, являющееся популярным средством для реализации модульного возведения в степень, включают такой алгоритм. По сравнению с затратами на операцию модульного возведения в степень затраты вычислительных ресурсов на выполнение такого алгоритма обычно незначительны.

До сих пор обсуждение было сконцентрировано на том случае, когда открытый модуль n является произведением двух простых чисел p и q. Эта ситуация - обычная для RSA-кодирования. Однако RSA-кодирование можно обобщить до модуля, который является произведением j простых чисел, где j - целое число, j≥2. Такое обобщение описано в патенте США №5848159. Данное изобретение относится к обобщенной схеме. Например, рассмотрим приложение с использованием КТО с простыми множителями p₁, p₂...p_j. Существует j случаев секретного показателя степени d, определенных как d_j=d mod (p_i-1) для i=1, 2,...,j. Чтобы применить данное изобретение, каждый d_j заменяют на k_j, когда сохраняется ключ, где k_j - такое значение, при которомk_j(p_i-1)mod e=1. Чтобы восстановить d_i из k_i, вычисляют d_i=1[1+(p_i-1)(e-k_i)]/e или d_i=[1+(1+(p_i-1)(e-k_i)]u_i mod 2^bi, где b_i - целое число, при котором p_i<2^bi, и u_i - значение, которое удовлетворяет eu_i mod 2^bi=1.

Доказательство формул для d_p, d_q и d. Сначала докажем, что формула

дает правильное значение для d_p, показав, что ed_p mod(p-1)=1.

Пусть a=1+(p-1)(e-k_p). Прежде всего надо показать, что a является кратным e, чтобы операция деления в формуле (1) давала целую величину. По определению, k_p(p-1) mod e=1. Следовательно, k_p(p-1)-1 является кратным e. Так как a=e(p-1)-[k_p(p-1)-1], следовательно, а является кратным e.

Теперь пусть d_p будет, как в (1). Тогда ed_p mod(p-1)=a mod (p-1)=1. Это доказывает формулу (1).

Теперь докажем, что формула

дает правильное значение для d_p, показав, что ed_p mod(p-1)=1.

Снова пусть a=1+(p-1)(e-k_p). Ранее было показано, что a является кратным e, поэтому мы можем записать a=ce, где с - целое число. Так как 0≤(p-1)<2^b и 0≤(e-k_p)≤e, следовательно, 0<a<e2^b, значит, 0<c<2^b. Теперь пусть d_p будет, как в формуле (2). Тогда

ed_p mod(p-1)

=e[au mod 2^b]mod(p-1)

=e[cue mod 2^b]mod(p-1)

=e[c mod 2^b]mod(p-1)

=ec mod(p-1)

=a mod(p-1)

=1.

Это доказывает формулу (2).

Доказательства формул

идентичны доказательствам формул (1) и (2), при этом d_q заменяет d_p, k_q заменяет k_p, и q заменяет p.

Доказательства формул

подобны доказательствам формул (1) и (2). Аргументы для формул (5) и (6) идентичны аргументам для формул (1) и (2), соответственно, при этом d заменяет d_p, k заменяет k_p, (p-1)(q-1) заменяет (p-1) и 2^2b заменяет 2^b. Вывод аргумента в каждом случае состоит в том, что ed mod(p-1)(q-1)=1. Из этого следует, что ed mod(p-1)=ed mod(q-1)=1.

Согласно первому аспекту изобретения предложено устройство для восстановления секретного ключа криптосистемы, содержащее процессор, объем энергонезависимой памяти, оперативно подключенной к процессору, и набор параметров секретного ключа, хранимый в объеме энергонезависимой памяти с использованием меньшего объема памяти, чем для полного набора параметров {p,q,d_p,d_q,v}, и обеспечивающий более высокую эффективность вычислений, чем с минимальным набором параметров {p,q}, причем секретный ключ может быть восстановлен из набора хранимых параметров секретного ключа.

Согласно другому аспекту изобретения предложен способ восстановления секретного ключа, заключающийся в том, что сохраняют параметры секретного ключа в объеме памяти, используют меньший объем памяти для параметров секретного ключа, чем для полного набора параметров {n,d}, и обеспечивают более высокую эффективность вычислений, чем с минимальным набором параметров {p,q}.

Краткое описание чертежей

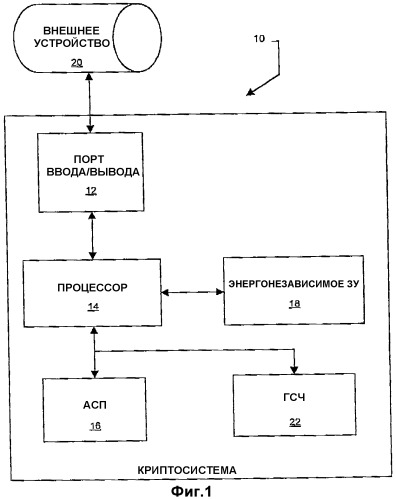
Фиг.1 схематически изображает вариант выполнения криптосистемы согласно настоящему изобретению;

фиг.2 изображает алгоритм первого примерного варианта осуществления настоящего изобретения;

фиг.3 изображает алгоритм второго примерного варианта осуществления настоящего изобретения;

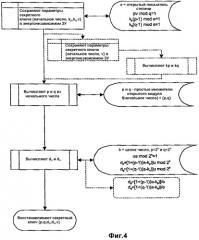
фиг.4 изображает алгоритм третьего примерного варианта осуществления настоящего изобретения;

фиг.5 изображает алгоритм четвертого примерного варианта осуществления настоящего изобретения;

фиг.6 изображает алгоритм пятого примерного варианта осуществления настоящего изобретения;

фиг.7 изображает алгоритм шестого примерного варианта воплощения настоящего изобретения;

фиг.8 изображает алгоритм седьмого примерного варианта воплощения настоящего изобретения.

Подробное описание изобретения

Специалистам будет понятно, что представленное ниже описание имеет только иллюстративный и ни в коем случае не ограничительный характер. На основании представленного описания специалисты легко смогут сами предложить другие варианты осуществления изобретения.

На фиг.1 изображена криптосистема 10, в которой могут быть реализованы преимущества настоящего изобретения. Криптосистема 10 осуществляет приложение подписи и декодирование сообщений, поступающих в нее через порт 12 ввода/вывода. Криптосистема 10 использует RSA-кодирование для приложения подписи и декодирования. Криптосистема 10 содержит процессор 14, который управляет всеми ее операциями. Криптосистема 10 содержит арифметический сопроцессор (АСП) 16, который облегчает вычисления, используемые в RSA-кодировании при приложении подписи и декодировании. Секретный ключ, используемый для приложения подписи и декодирования, хранится в энергонезависимом запоминающем устройстве 18 в криптосистеме 10.

Криптосистема 10 выполнена с возможностью хранения набора секретных ключей в энергонезависимом запоминающем устройстве 18 и выбора секретного ключа для использования в целях конкретного приложения подписи или декодирования в соответствии с командами, введенными в нее через порт 12 ввода/вывода. Криптосистема 10 способна вычислять открытый ключ, который соответствует любому секретному ключу, хранимому в энергонезависимом запоминающем устройстве 18, и передавать открытый ключ во внешнее устройство 20 через порт 12 ввода/вывода.

Криптосистема 10 выполнена с возможностью формирования секретных ключей и их сохранения в энергонезависимом запоминающем устройстве 18. При формировании секретного ключа криптосистема использует генератор случайных чисел (ГСЧ) 22, чтобы обеспечить произвольный выбор простых множителей p и q секретного ключа. ГСЧ 22 обеспечивает произвольное начальное число, которое подается в алгоритм, формирующий p и q. При сохранении секретного ключа криптосистема 10 может вместо сохранения p и q сохранить начальное число и восстанавливать значения p и q посредством применения алгоритма к начальному числу каждый раз, когда данный секретный ключ используется для приложения подписи или декодирования.

Криптосистема 10 также способна принимать секретные ключи, передаваемые в нее внешними устройствами 20, через порт 12 ввода/вывода и сохранять секретные ключи в энергонезависимом запоминающем устройстве 18. Переданный извне секретный ключ может быть сам по себе зашифрован внешним устройством с использованием открытого ключа, который соответствует одному из секретных ключей, уже присутствующих в энергонезависимом запоминающем устройстве 18 криптосистемы 10. В таком случае криптосистема 10 дешифрует зашифрованный секретный ключ, используя секретный ключ, уже имеющийся в энергонезависимом запоминающем устройстве 18, а затем сохраняет дешифрованный секретный ключ в энергонезависимом запоминающем устройстве 18.

Независимо от того, формируется ли секретный ключ криптосистемой 10 или подается внешним устройством 20, криптосистема 10 способна использовать настоящее изобретение для уменьшения объема энергонезависимого запоминающего устройства 18, необходимого для хранения секретного ключа, и быстрого восстановления секретного ключа без увеличения уязвимости защиты. Криптосистема 10 имеет множество соответствующих вариантов применения изобретения, обеспечивающего компромисс между объемом памяти и скоростью восстановления.

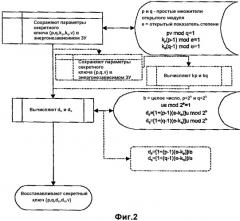
В первом примере, проиллюстрированном на фиг.2, сначала сохраняют параметры секретного ключа как {p,q,k_p,k_q,v}, где p и q - простые множители открытого модуля; v - значение, удовлетворяющее pv mod q=1; k_p - значение, удовлетворяющее k_p(p-1)mod e=1, где e - открытый показатель степени и k_q - значение, удовлетворяющее k_q(q-1)mod e=1. Для восстановления секретного ключа в обычной форме с использованием КТО {p,q,d_p,d_q,v}, где d_p=d mod(p-1), d_q=d mod(q-1) и d - секретный показатель степени, вычисляют d_p=[1+(p-1)(e-k_p)]u mod 2^b, d_q=[1+(q-1)(e-k_q)]u mod 2^b, где b - целое число, так что p<2^b и q<2^b, и u - значение, удовлетворяющее ue mod 2^b=1.

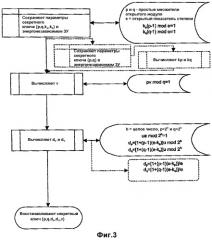
Во втором примере, проиллюстрированном на фиг.3, сначала сохраняют набор параметров секретного ключа как {p,q,k_p,k_q,v}, где p,q,k_p и k_q - как в первом примере. Для восстановления секретного ключа сначала вычисляют значение v, удовлетворяющее pv mod q=1. Затем переходят к использованию {p,q,k_p,k_q,v}, как в первом примере.

В третьем примере, проиллюстрированном на фиг.4, сначала сохраняют параметры секретного ключа как {начальное число, k_p,k_q,v}, где начальное число - ввод в алгоритм, который формирует простые множители p и q открытого модуля; и k_p k_q и v - как в первом примере. Для восстановления секретного ключа сначала применяют алгоритм к начальному числу для восстановления значений p и q. Затем переходят к использованию {p,q,k_p,k_q,v} как в первом примере. Известно множество алгоритмов для начального числа. См., например, алгоритмы, которые формируют простые числа произвольного начального числа, в Приложении 2 документа [FIPS186] Департамента торговли США /Национального института стандартов и технологии "Стандарт цифровой подписи", FIPS PUB 186-2, 27 января 2000 г.

В четвертом примере, проиллюстрированном на фиг.5, сначала сохраняют параметры секретного ключа как {начальное число, k_p,k_q}, где начальное число, k_p,k_q - как в третьем примере. Для восстановления секретного ключа сначала применяют алгоритм к начальному числу для восстановления значений p и q. Затем переходят к использованию {p,q,k_p,k_q}, как во втором примере.

В альтернативном варианте сначала сохраняют параметры секретного ключа, используя любые форматы, описанные в приведенных выше четырех примерах. При восстановлении секретного ключа вместо использования вычислений для d_p и d_q, описанных в предыдущих примерах, вычисляют d_p=[1+(p-1)(e-k_p)]/e и d_q=[1+(q-1)(e-k_q)]/e. Также, в другой альтернативе предыдущих примеров вместо сохранения k_p и k_q, их можно вычислить из p, q и e. Каждое из них можно вычислить с помощью алгоритма Евклида или его известного варианта, хотя это может обусловить уязвимость защиты, так как последовательность операций зависит от p и q. Альтернативно, в случае, когда е - простое число, как в распространенном значении e=2¹⁶+1, каждый параметр можно вычислить с использованием модульного возведения в степень, используя формулы k_p=(p-1)^e-2mod e и k_q=(q-1)^e-2mod e; что не приводит к увеличению уязвимости защиты, потому что последовательность операций можно сделать независимой от p и q. Так как е - малое число, затраты вычислительных ресурсов на k_p и k_q часто пренебрежимо малы по сравнению с затратами на RSA-операцию секретного ключа.

В пятом примере, проиллюстрированном на фиг.6, сначала сохраняют параметры секретного ключа как {p,q,k}, где p и q - простые множители открытого модуля, а k - значение, удовлетворяющее k(p-1)(q-1)mod e=1, где e - открытый показатель степени. Для восстановления секретного ключа в обычной форме {n,d} без использования КТО, где n - открытый модуль, а d - секретный показатель степени, вычисляют n=pq и d=[1+(p-1)(q-1)]t mod 2^2b, где b - целое число, так что p<2^b и q<2^b, и t - значение, удовлетворяющее te mod 2^2b=1.

В шестом примере, проиллюстрированном на фиг.7, сначала сохраняют параметры секретного ключа, используя формат пятого примера. При восстановлении секретного ключа вместо использования вычисления d, описанного в пятом примере, вычисляют d=[1+(p-1)(q-1)]/e.

В седьмом примере, проиллюстрированном на фиг.8, сначала сохраняют параметры секретного ключа, используя формат пятого примера. При восстановлении секретного ключа сначала вычисляют секретный показатель степени d, используя вычисление по любому из предыдущих двух (пятого или шестого) примеров. Затем для восстановления секретного ключа в обычном формате с использованием КТО {p,q,d_p,d_q,v} вычисляют d_p=d mod(p-1) и d_q=d mod(q-1) и вычисляют значение v, удовлетворяющее pv mod q=1.

Несмотря на то, что выше были описаны и проиллюстрированы варианты осуществления и применения изобретения, специалистам будет понятно, что возможны и другие модификации, не выходящие за пределы раскрытого изобретательского замысла. Поэтому настоящее изобретение ограничено только прилагаемой формулой изобретения.

1. Устройство для восстановления секретного ключа криптосистемы, содержащее процессор, энергонезависимую память, оперативно связанную с упомянутым процессором, и набор параметров секретного ключа, хранимый в упомянутой энергонезависимой памяти, причем секретный ключ может быть восстановлен из упомянутого хранимого набора параметров секретного ключа, при этом упомянутый набор параметров секретного ключа содержит параметр k_p, причем упомянутый параметр k_p получен из k_p(p-1)mod e=1, где р - простой множитель открытого модуля, е - заданный открытый показатель степени.

2. Устройство по п.1, отличающееся тем, что упомянутый набор параметров секретного ключа определен параметрами {р, q, k_p, k_q, v}, где q - заданный простой множитель открытого модуля, k_q получен из k_q(q-1)mod e=1 и v получен из pv mod q=1.

3. Устройство по п.2, отличающееся тем, что дополнительно содержит вычислитель d_p, взаимодействующий с процессором и выполненный с возможностью вычисления d_p из d_p=[1+(p-1)(e-k_p)]u mod 2^b, вычислитель d_q, взаимодействующий с процессором и выполненный с возможностью вычисления d_q из d_q=[1+(q-1)(e-k_q)]u mod 2^b, и где b - целое число такое, что р меньше, чем 2^b, и q меньше, чем 2^b, и ue mod 2^b=1.

4. Устройство по п.3, отличающееся тем, что дополнительно содержит блок сбора параметров секретного ключа для сбора параметров {р, q, d_p, d_q, v} секретного ключа из упомянутых хранимых и вычисленных значений.

5. Устройство по п.2, отличающееся тем, что дополнительно содержит вычислитель d_p, взаимодействующий с процессором и выполненный с возможностью вычисления d_p из d_p=[1+(p-1)(e-k_p)]/e, и вычислитель d_q, взаимодействующий с процессором и выполненный с возможностью вычисления d_q из d_q=[1+(q-1)(e-k_q)]/e.

6. Устройство по п.5, отличающееся тем, что дополнительно содержит блок сбора параметров секретного ключа для сбора параметров секретного ключа {р, q, d_p, d_q, v} из упомянутых хранимых и вычисленных значений.

7. Устройство по п.1, отличающееся тем, что упомянутый набор параметров секретного ключа определен параметрами {р, q, k_p, k_q}, где q - заданный простой множитель открытого модуля и k_q получен из k_q(q-1)mod е=1.

8. Устройство по п.7, отличающееся тем, что дополнительно содержит вычислитель v, взаимодействующий с процессором и выполненный с возможностью вычисления v из pv mod q=1.

9. Устройство по п.8, отличающееся тем, что дополнительно содержит вычислитель d_p, взаимодействующий с процессором и выполненный с возможностью вычисления d_p из d_p=[1+(p-1)(e-k_p)]u mod 2^b, вычислитель d_q, взаимодействующий с процессором и выполненный с возможностью вычисления d_q из d_q=[1+(q-1)(e-k_q)u mod 2^b, и где b - целое число такое, что р меньше, чем 2^b, и q меньше, чем 2^b, и ue mod 2^b=1.

10. Устройство по п.9, отличающееся тем, что дополнительно содержит блок сбора параметров секретного ключа для сбора параметров секретного ключа (р, q, d_p, d_q, v} из упомянутых хранимых и вычисленных значений.

11. Устройство по п.8, отличающееся тем, что дополнительно содержит вычислитель d_p, взаимодействующий с процессором и выполненный с возможностью вычисления d_p из d_p=[1+(p-1)(e-k_p)]/e, и вычислитель d_q, взаимодействующий с процессором и выполненный с возможностью вычисления d_q из d_q=[1+(q-1)(e-k_q)]/e.

12. Устройство по п.11, отличающееся тем, что дополнительно содержит блок сбора параметров секретного ключа для сбора параметров секретного ключа {р, q, d_p, d_q, v} из упомянутых хранимых и вычисленных значений.

13. Устройство по п.1, отличающееся тем, что упомянутый набор параметров секретного ключа определен параметрами {начальное число, k_p, k_q, v}, где k_q получен из k_q(q-1)mod е=1 и v получен из pv mod q=1, a начальное число является значением, полученным из генератора случайных чисел.

14. Устройство по п.13, отличающ