Способ определения модулей упругости бериллиевой бронзы бр.б2

Способ определения модулей упругости бериллиевой бронзы бр.б2

Иллюстрации

Показать все

Реферат

Изобретение относится к металлургии, в частности к методам измерения модулей упругости бериллиевой бронзы.

Предлагаемый способ измерения модулей упругости может быть использован для контроля качества упругих элементов после термической и пластической обработки.

Бериллиевая бронза обладает оптимальными электрическими, антикоррозионными, прочностными и упругими характеристиками, в связи с чем данный материал находит большое применение в приборостроении, компьютерной технике, в автомобильной и электронной промышленности для изготовления контактных упругих элементов. С целью получения оптимального сочетания прочностных, пластических и упругих характеристик упругие элементы, изготовленные из бериллиевой бронзы (Бр.Б2), подвергаются термической обработке, при этом контроль качества готовых элементов производится путем замера их твердости [1], которая является показателем прочности. Однако, как показала практика, при соблюдении рекомендаций по применению режимов проведения операции термической обработки можно получить одну партию деталей менее прочную, чем другую, но обе партии будут считаться качественными. Согласно утверждению А.Г. Рахштадта и его коллег [2], измерение твердости является всего лишь методом определения качества процесса термообработки, а не качества детали. Кроме того, для пружин наиболее информативными показателями являются модули упругости, так как именно они в основном участвуют в расчетах на стадии проектирования и характеризуют качество упругих элементов в большей степени, чем твердость.

На стадии проектирования расчет упругих элементов проводится на основе данных об их линейных размерах и модулях упругости [3]. Кроме того, знание модулей упругости необходимо для определения частоты собственных колебаний, жесткости и некоторых других параметров, характеризующих свойства пружины. Модули упругости являются структурно-чувствительными параметрами [4] и, следовательно, получить их определенное значение можно путем выбора исходного состояния материала (мягкое или твердое) и режимов дисперсионного твердения [5].

Иначе говоря, выбрав оптимальный режим термообработки, можно получить конкретное, заданное, значение модуля нормальной упругости или модуля сдвига. И следовательно, контроль качества детали после термообработки можно проводить именно по значениям требуемого параметра, т.е. по значению модуля упругости, что является более целесообразным.

Существуют два основных метода определения модулей упругости - статический и динамический [6]. Статический метод основан на испытании образцов на растяжение с использованием тензометров. В зависимости от типа тензометра метод подразделяется на механический, пневматический, оптический и др. Подобными методами модули упругости определяются с относительной погрешностью 2-4%. При этом сам процесс определения модулей упругости является сложным и непроизводительным.

Динамический метод, по сравнению со статическим, является более точным, более производительным и к тому же неразрушающим. Динамический метод основан на определении скорости распространения проходящих через сечение материала продольных и поперечных ультразвуковых волн. Относительная погрешность динамического метода не превышает 0,2% и поэтому данный метод является предпочтительным. Кроме того, этот метод можно применять на конкретной детали, а не на образце-свидетеле.

Сущность динамического метода определения модулей упругости состоит в следующем.

Через сечение изделия последовательно пропускают продольные и поперечные волны, принимают эхо-сигналы, измеряют время их прихода и при известной толщине детали h определяют скорости распространения продольных V_l и поперечных V_τ - волн в детали по формулам:

где V_l и V_τ - скорости продольной и поперечной волн, проходящих через деталь, м/сек.

Модуль нормальной упругости определяется по формуле [7]

где

ρ - плотность материала, кг/м³;

μ - коэффициент Пуассона, определяемый из соотношения [7]

Модуль сдвига рассчитывается по формуле [7]

Как видно из формулы (3), модуль нормальной упругости прямо пропорционален значению плотности, которая в процессе пластической или термической обработки изменяется на 0,5-1,2%. Поэтому для более точного определения модуля нормальной упругости требуется учитывать изменение плотности в процессе обработки.

Таким образом, динамический метод определения модулей упругости, являясь менее трудоемким и более производительным по сравнению со статическим методом, все-таки затруднителен для применения его в производстве, так как требует одновременного экспериментального определения нескольких параметров, специализированного оборудования и довольно сложных расчетов.

Техническим результатом предлагаемого изобретения является возможность определения модулей упругости по формулам с экспериментальным определением только одного параметра (скорости поперечных волн), без измерения плотности изготавливаемой детали и без применения сложных математических расчетов.

Сущность изобретения заключается в следующем. Для определения значений модулей упругости, например при контроле упрочненной детали, через ее толщину попускают поперечный тип ультразвуковой волны и определяют время ее прохождения через деталь. Определяют скорость пропускаемой поперечной волны и по нижеприведенным формулам (8) или (10) вычисляют модули упругости.

Была проведена работа, в ходе которой экспериментально определялись зависимость изменения модуля нормальной упругости Е (ГПа) и модуля сдвига G (ГПа) бериллиевой бронзы марки Бр.Б2 от режимов ее термической и пластической обработки. Для определения зависимости использовались цилиндрические образцы, которые подвергались закалке при температуре 780±4°С, деформации на 0%, 20% и 40% и старению при температурах 320±2°С и 340±2°С продолжительностью от 0 до 4 часов, с шагом 0,5 часа. Всего на каждой точке испытывалось не менее пяти образцов, полученные результаты усреднялись. При этом значения модулей упругости определялись известным динамическим методом, а именно через обработанные образцы пропускались продольные и поперечные ультразвуковые волны, измерялись скорости их прохождения через образец, методом гидростатического взвешивания определялись значения плотности образцов и по известным формулам (3-5) рассчитывались модули упругости. Полученные в ходе эксперимента значения модулей нормальной упругости, модулей упругости при сдвиге, плотности, режимы термообработки и скорости поперечных волн (считается, что поперечные волны наиболее структурно-чувствительные) приведены в таблице 1.

Таблица 1
Состояние	ρ, кг/м3	Vτ, м/сек	Е, ГПа	G, ГПа
Закалка 780°С, деформация 0%
Старен. 320°С, 0 ч	8214,3	2299	118	43
Старен. 320°С, 0,5 ч	8274,6	2344	123	45
Старен. 320°С, 1 ч	8308,0	2389	128	47
Старен. 320°С, 1,5 ч	8308,3	2397	129	48
Старен. 320°С, 2 ч	8308,3	2404	129	48
Старен. 320°С, 2,5 ч	8308,7	2408	130	48
Старен. 320°С, 3 ч	8309,7	2410	130	48
Старен. 320°С, 4 ч	8309,8	2413	130	48
Старен. 340°С, 0 ч	8214,3	2299	118	43
Старен. 340°С, 0,5 ч	8299,1	2388	128	47
Старен. 340°С, 1 ч	8301,1	2399	129	48
Старен. 340°С, 1,5 ч	8301,7	2413	130	48
Старен. 340°С, 2 ч	8301,0	2418	131	49
Старен. 340°С, 2,5 ч	8304,0	2420	131	49
Старен. 340°С, 3 ч	8309,6	2420	131	49
Старен. 340°С, 4 ч	8313,7	2426	132	49

Продолжение таблицы 1
Состояние	ρ, кг/м3	Vτ м/сек	Е, ГПа	G, ГПа
Закалка 780°С, деформация 20%
Старен. 320°С, 0 ч	8229,3	2304	119	44
Старен. 320°С, 0,5 ч	8297,7	2363	125	46
Старен. 320°С, 1 ч	8314,4	2400	129	48
Старен. 320°С, 1,5 ч	8317,7	2406	130	48
Старен. 320°С, 2 ч	8316,7	2412	130	48
Старен. 320°С, 2,5 ч	8317,0	2413	130	48
Старен. 320°С, 3 ч	8317,3	2414	131	48
Старен. 320°С, 4 ч	8317,0	2415	131	48
Старен. 340°С, 0 ч	8229,3	2304	119	44
Старен. 340°С, 0,5 ч	8303,0	2396	128	48
Старен. 340°С, 1 ч	8305,5	2408	130	48
Старен. 340°С, 1,5 ч	8303,1	2419	131	49
Старен. 340°С, 2 ч	8304,2	2424	131	49
Старен. 340°С, 2,5 ч	8308,8	2424	131	49
Старен. 340°С, 3 ч	8313,7	2429	132	49
Старен. 340°С, 4 ч	8311,2	2432	132	49
Закалка 780°С, деформация 40%
Старен. 320°С, 0 ч	8255,2	2310	119	44
Старен. 320°С, 0,5 ч	8304,7	2369	126	47
Старен. 320°С, 1 ч	8317,2	2405	129	48
Старен. 320°С, 1,5 ч	8319,0	2411	130	48
Старен. 320°С, 2 ч	8318,5	2417	130	49
Старен. 320°С, 2,5 ч	8317,4	2418	131	49
Старен. 320°С, 3 ч	8318,6	2419	131	49
Старен. 320°С, 4 ч	8318,1	2420	131	49
Старен. 340°С, 0 ч	8255,2	2310	119	44
Старен. 340°С, 0,5 ч	8304,6	2402	129	48
Старен. 340°С, 1 ч	8305,9	2415	130	48
Старен. 340°С, 1,5 ч	8305,4	2428	131	49
Старен. 340°С, 2 ч	8304,5	2434	132	49
Старен. 340°С, 2,5 ч	8310,6	2438	132	49
Старен. 340°С, 3 ч	8315,3	2440	133	50
Старен. 340°С, 4 ч	8313.3	2441	133	50

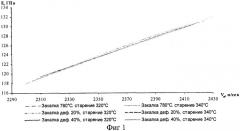
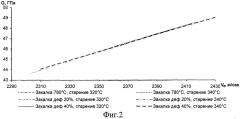
Анализ результатов эксперимента показал, что зависимость модулей упругости от скорости поперечных волн носит линейный характер (фиг.1 и 2). Следовательно, модуль нормальной упругости можно выразить формулой:

Экстраполируя уравнение (6) и принимая V_τ0=0, получим выражение для модуля нормальной упругости:

,

где к - коэффициент, равный тангенсу угла наклона прямой графика зависимости модуля нормальной упругости от скорости поперечных волн к оси абсцисс. Для модуля нормальной упругости tgα=0.1086, а Е₀≈-132 ГПа;

Подставляя полученные коэффициенты в уравнение (7), получим значение модуля нормальной упругости в ГПа,

Аналогично, при Е_o=0 выражение (6) в конечном итоге приобретает вид:

Подобным же образом получим выражение зависимости модуля сдвига в ГПа от скорости поперечных волн.

В таблице 2 приведены значения модулей упругости, определенных динамическим методом и предлагаемым способом, а также расхождение их значений в %.

Таблица 2
Состояние	Eэксп., ГПа	Eрасч. ГПа	δ, %	Gэксп., ГПа	Gрасч. ГПа	δ, %
Закалка 780°С, деформация 0%
Старен. 320°С, 0 ч.	118	117,7	0,16	43	43,4	0,132
Старен. 320°С, 0,5 ч.	123	122,6	0,49	45	45,4	0,275
Старен. 320°С, 1,0 ч.	128	127,5	0,44	47	47,3	0,210
Старен. 320°С, 1,5 ч.	129	128,3	0,32	48	47,7	0,142
Старен. 320°С, 2,0 ч.	129	129,0	0,24	48	48,0	0,084
Старен. 320°С, 2,5 ч.	130	129,6	0,22	48	48,2	0,050
Старен. 320°С, 3,0 ч.	130	129,8	0,22	48	48,3	0,045
Старен. 320°С, 4,0 ч.	130	130,0	0,16	48	48,4	0,026
Старен. 340°С, 0 ч.	118	117,7	0,16	43	43,4	0,132
Старен. 340°С, 0,5 ч	128	127,3	0,17	47	47,3	0,115
Старен. 340°С, 1,0 ч.	129	128,5	0,14	48	47,7	0,043
Старен. 340°С, 1,5 ч.	130	130,0	0,00	48	48,4	0,070
Старен. 340°С, 2,0 ч.	131	130,6	0,07	49	48,6	0,121
Старен. 340°С, 2,5 ч.	131	130,8	0,01	49	48,7	0,099
Старен. 340°С, 3,0 ч.	131	130,8	0.07	49	48,7	0,034
Старен. 340°С, 4,0 ч.	132	131,4	0,07	49	48,9	0,026
Закалка 780°С, деформация 20%
Старен. 320°С, 0 ч.	119	118,2	0,29	44	43,6	0,247
Старен. 320°С, 0,5 ч.	125	124,6	0,52	46	46,2	0,345
Старен. 320°С, 1,0 ч.	129	128,7	0,37	48	47,8	0,186
Старен. 320°С, 1,5 ч.	130	129,3	0,37	48	48,1	0,179
Старен. 320°С, 2,0 ч.	130	129,9	0,29	48	48,3	0,119
Старен. 320°С, 2,5 ч.	130	130,0	0,28	48	48,4	0,113
Старен. 320°С, 3,0 ч.	131	130,2	0,31	48	48,4	0,106
Старен. 320°С, 4,0 ч.	131	130,2	0,26	48	48,4	0,099
Старен. 340°С, 0 ч.	119	118,2	0,29	44	43,6	0,247
Старен. 340°С, 0,5 ч	128	128,2	0,15	48	47,6	0,089
Старен. 340°С, 1,0 ч.	130	129,5	0,06	48	48,2	0,013
Старен. 340°С, 1,5 ч.	131	130,7	0,07	49	48,6	0,099
Старен. 340°С, 2,0 ч.	131	131,2	0,15	49	48,8	0,127
Старен. 340°С, 2,5 ч.	131	131,2	0,02	49	48,9	0,072
Старен. 340°С, 3,0 ч.	132	131,8	0,03	49	49,1	0,052
Старен. 340°С, 4,0 ч.	132	132,1	0,08	49	49,2	0,104

Продолжение таблицы 2
Состояние	Eэксп., ГПа	Eрасч. ГПа	δ, %	Gэксп., ГПа	Gрасч. ГПа	δ, %
Закалка 780°С, деформация 40%
Старен. 320°С, 0 ч.	119	118,8	0,47	44	43,8	0,482
Старен. 320°С, 0,5 ч.	126	125,3	0,24	47	46,4	0,367
Старен. 320°С, 1,0 ч.	129	129,2	0,07	48	48,0	0,177
Старен. 320°С, 1,5 ч.	130	129,9	0,03	48	48,3	0,149
Старен. 320°С, 2,0 ч.	130	130,5	0,03	49	48,5	0,099
Старен. 320°С, 2,5 ч.	131	130,6	0.05	49	48,6	0,074
Старен. 320°С, 3,0 ч.	131	130,7	0,04	49	48,6	0,085
Старен. 320°С, 4,0 ч.	131	130,8	0,07	49	48,7	0,073
Старен. 340°С, 0 ч.	119	118,8	0,47	44	43,8	0,482
Старен. 340°С, 0.5 ч	129	128,8	0,03	48	47,9	0,056
Старен. 340°С, 1,0 ч.	130	130,2	0,04	48	48,4	0,034
Старен. 340°С, 1,5 ч.	131	131,7	0,28	49	49,0	0,144
Старен. 340°С, 2,0 ч.	132	132,3	0,20	49	49,3	0,197
Старен. 340°С, 2,5 ч.	132	132,8	0,22	49	49,5	0,152
Старен. 340°С, 3,0 ч.	133	133,0	0,20	50	49,6	0,111
Старен. 340°С, 4,0 ч.	133	133,1	0,24	50	49,6	0,142

Сопоставление значений модулей упругости, рассчитанных динамическим методом и предлагаемым способом, показало, что относительное расхождение значений не превышает 0,5%. Кроме того, из таблицы 2 видно, что формулы (8) и (10) справедливы независимо от степени деформации и режима термической обработки.

Предлагаемый способ был проверен на натурных деталях (плоских пружинах и цангах). Разница между результатами данных, полученных предлагаемым способом и динамическим методом, не превышает 0,6% при существенном упрощении самого процесса определения модулей упругости.

Предлагаемый способ определения модулей упругости проверен только на бериллиевой бронзе марки Бр.Б2, но тем не менее практическая ценность подобного метода высока, так как позволяет рассчитывать упругие модули, определяя только скорость поперечных волн, избегая при этом определения плотности, скорости продольных волн и сложных математических расчетов.

Предлагаемый способ может применяться при контроле качества упругих элементов по упругим константам неразрушающим методом по более информативным параметрам сами детали, а не образцы-свидетели.

ЛИТЕРАТУРА

1. Р4. 054. 035 - 89 «Рекомендации. Элементы пружинные из сплавов черных и цветных металлов. Термическая обработка».

2. Ж.П.Пастухова, А.Г.Рахштадт.Пружинные сплавы цветных металлов. М., «Металлургия», 1983.

3. ОСТ4 Г0.838.200 «Пружины. Методика расчета и указания по проектированию».

4. В.В.Муравьев, Л.Б.Зуев, К.Л.Комаров. Скорость звука и структура сталей и сплавов. Новосибирск: Наука. Сибирская издательская фирма РАН, 1996.

5. Заявка №2004108589 на выдачу патента РФ на изобретение «Способ выбора режимов термической обработки бериллиевой бронзы марки Бр.Б2» с приоритетом от 13.04.2004 г.

6. М.Л.Берштейн, А.Г.Рахштадт.Металловедение и термическая обработка стали. Справочник в 3-х томах. Том 1 «Методы испытаний и исследования». Изд.3 перераб. и доп. М., «Металлургия», 1983.

7. «Испытание материалов», Справ. Изд под ред. X.Блюменауэра. М., «Металлургия», 1979.

Способ определения модуля нормальной упругости (Е) и модуля сдвига (G) бериллиевой бронзы Бр.Б2, справедливый для различных степеней деформации и режимов термической обработки деталей и обеспечивающий достаточно высокую точность значений определяемых модулей, заключающийся в том, что через деталь пропускают только поперечный тип ультразвуковой волны, определяют скорость ее прохождения (V_τ) через деталь и вычисляют модуль нормальной упругости и модуль сдвига по формулам Е=0.1086·V_τ-132 (ГПа), G=0.044·V_τ-57.8 (ГПа).