Способ и устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области

Способ и устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области гидролокации и радиолокации, а именно к способам обнаружения сложных широкополосных частотно-модулированных сигналов на фоне аддитивной помехи и реализующим их устройствам.

Известно, что реализация оптимального приема при решении задачи обнаружения сигналов на фоне помех во многом определяется уровнем знаний о принимаемом сигнале.

Для сигналов с неизвестной начальной фазой оптимальным является квадратурный приемник [2-5] (аналог), обеспечивающий незначительные потери (1-1.2 дБ) по сравнению с согласованной фильтрацией. Основным недостатком квадратурного приема является ограниченность его применения только для класса узкополосных сигналов. В случае использования широкополосных сигналов необходима многоканальная схема, осуществляющая квадратурную фильтрацию по каждой составляющей.

Если фазовый спектр сигнала неизвестен, то используют энергетические методы и устройства приема [2-5] (аналог), представляющие собой последовательное выполнение операций фильтрации, квадратичного детектирования и интегрирования. Недостатком таких методов является "эффект подавления малого сигнала", что является следствием того факта, что выходное отношение сигнал/помеха (ОСП) пропорционально квадрату входного ОСП.

Если же форма принимаемого сигнала известна (за исключением амплитуды a и времени прихода сигнала t₀: a·s(t-t₀)), то потенциальную помехоустойчивость при решении задачи обнаружения сигналов (в том числе и широкополосных частотно-модулированных) на фоне белого шума, в принципе, обеспечивает корреляционный приемник или согласованная фильтрация [1 (с.339-343)] (прототип), [2-5].

Причем помехоустойчивость этих обоих методов обнаружения сигналов в теоретическом смысле абсолютно одинакова. Обобщенное отношение сигнал/помеха (ОСП) на выходе этих обнаружителей (определяемое как отношение приращения математического ожидания выходного процесса y(t), обусловленное наличием полезного сигнала, к дисперсии выходного процесса в случае отсутствия сигнала) равно отношению удвоенной энергии сигнала Е (с учетом случайной амплитуды) к спектральной плотности помехи N [1]:

Данный метод обнаружения известного сигнала неявно предполагает один из видов одномерного представления сигнала и помехи: либо в спектральной области (согласованная фильтрация), либо во временной области (корреляционный прием).

Однако для входного процесса x(t) гидролокационного или радиолокационного приемника возможно также и двумерное представление - в масштабно-временной области, получаемое путем применения т.н. непрерывного вейвлет-преобразования (ВП) [6-10].

Непрерывное ВП можно определить как скалярное произведение исследуемого процесса x(t) и базисных функций ψ_ατ(t) [6]:

где черта сверху обозначает операцию комплексного сопряжения.

Общий принцип построения базиса ВП состоит в использовании масштабных преобразований с параметром сжатия α и смещений с параметром сдвига τ исходной вейвлет-функции ψ(t) (т.н. материнского вейвлета):

Чтобы быть вейвлетом, базисные функции ψ_ατ(t)∈L²(R) должны обладать рядом необходимых свойств [6-10]. Они должны быть: квадратично-интегрируемыми, знакопеременными (и обладать нулевым средним), вейвлеты должны стремиться к нулю на ±∞, и для практических целей - чем быстрее, тем лучше (причем вейвлет должен быть хорошо локализован и во времени, и по частоте). Для того чтобы было возможно обратное ВП, спектральная функция вейвлета должна удовлетворять еще одному условию:

Формула непрерывного обратного вейвлет-преобразования имеет вид:

Как видно из (4), исходный сигнал x(t) может быть восстановлен через интегральную сумму тех же базисных функций ψ_ατ(t) с весами в виде вейвлет-спектра сигнала [W_ψx](α,τ). Здесь константа С_ψ (3) выступает как нормирующий коэффициент, аналогичный коэффициенту (2π)^1/2, нормирующему преобразование Фурье.

С целью более эффективного вычисления операторы прямого (1) и обратного (4) ВП могут быть представлены в частотной области. При этом достигается значительное повышение быстродействия цифровых устройств, реализующих ВП, за счет вычисления сверток с помощью эффективных процедур БПФ.

Оператор (1) непрерывного прямого ВП может быть определен в частотной области [6 (с.59, 67-68), 12] (аналог) в виде:

где: - образ Фурье выбранного исходного вейвлета ψ(t),

- образ Фурье анализируемого процесса x(t).

Оператор (4) непрерывного обратного ВП также может быть определен в частотной области в виде:

где: - преобразование Фурье от вейвлет-спектра процесса x(t).

Единственным ограничением для данной формы записи операторов (5) и (6) непрерывного ВП по сравнению с (1) и (4) является требование аналитичности для исследуемого сигнала и применяемого вейвлета [1 (с.67-68)]:

т.е.

В случае вейвлет-анализа действительных сигналов (что имеет место при обработке радиолокационных и гидролокационных сигналов) их легко представить в аналитическом виде, без потери информации, путем обнуления отрицательных частот их комплексных спектров Фурье. То же самое касается и используемых вейвлетов. Причем часть широко применяемых комплексных вейвлетов (например, вейвлет Морле) уже по определению сами являются аналитическими сигналами.

В принципе, для реализации операторов (5) и (6) достаточно, чтобы аналитическим был только вейвлет, т.к. свертка анализируемого сигнала с аналитическим вейвлетом (что соответствует перемножению их спектров) в итоге также дает результирующий аналитический сигнал.

В настоящее время применяется большое количество различных семейств вейвлетов: Хаара, Добеши, Морле, FHAT, МНАТ и т.д. [6-10]. Выбор типа анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из сигнала, и степенью схожести вейвлета и анализируемого сигнала. Каждый вейвлет имеет свои характерные особенности во временном и частотном пространстве. С помощью различных типов вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала в масштабно-временной плоскости.

В частности, для вейвлет-анализа детерминированных частотно-модулированных сигналов (например, сигналов с линейной частотной модуляцией (ЛЧМ) или с гиперболической частотной модуляцией (ГЧМ), широко применяемых в гидро- и радиолокации) одним из наиболее подходящих (с точки зрения схожести с сигналом) является комплексный аналитический вейвлет Морле (Morlet) [6-10], который конструируется на основе комплексной экспоненты, модулированной гауссианом единичной ширины:

,

где: ω₀ - параметр, определяющий количество волн в вейвлете.

Преобразование Фурье данного типа вейвлетов имеет вид:

,

где: Θ(ω) - функция Хэвисайда.

Вейвлет-спектр Ws(α,τ) одномерного сигнала s(t), полученный в результате ВП, является двухмерной функцией и представляет собой поверхность в трехмерном пространстве. При анализе результатов преобразования вместо изображения поверхностей часто рассматривают их проекции на плоскость (α,τ) с изолиниями, позволяющими проследить изменение амплитуд ВП на разных масштабах и в различные моменты времени. Способы визуализации этой информации в плоском случае могут быть различны - цвет, яркость или изолинии. В тех случаях, когда нужно показать очень широкий диапазон масштабов, применяют логарифмические координаты для коэффициента сжатия (log α,τ).

Интерес для цифровой обработки сигналов представляет дискретный вариант ВП [6, 8, 9, 12]. Необходимая дискретизация значений α и τ при сохранении возможности восстановления сигнала из его преобразования должна осуществляться следующим образом:

Вместо экспоненциальной дискретизации масштабных коэффициентов возможна и линейная дискретизация вида:

Дискретный вариант базиса вейвлетов (2) с дискретизацией α и τ вида (7):

в математической литературе [6] называют фреймами.

Шкала масштабов вейвлет-спектра однозначно соответствует частотам Фурье исследуемого сигнала. Поэтому ВП можно трактовать и как особый вид частотно-временного представления сигналов. Причем линейная шкала масштабов (8) более удобна для сравнения результатов ВП с другими видами частотно-временных представлений сигналов.

Известно большое количество других видов частотно-временного представления сигналов (Габора, Пейджа, Вигнера, Цзуя-Уильямса и т.д.) [11], однако все они (в отличие от ВП) обладают худшими локализующими свойствами в частотно-временной плоскости (имеют место ложные элементы и плохая одновременная различимость дельта-импульсов и тональных сигналов) и не всегда имеют обратное преобразование для точного восстановления исходного временного сигнала. Соответственно, данные методы частотно-временного представления обычно применяются лишь для анализа сигналов, но не для решения задач обнаружения.

Теоретические основы предлагаемого способа

Применение масштабно-временного представления (на основе ВП) к входному процессу x(t) обнаружителя сигналов:

где: s(t) - обнаруживаемый эхо-сигнал,

n(t) - аддитивная помеха в виде гауссового белого шума, позволяет (до непосредственной операции согласованной фильтрации) реализовать предварительную "полосовую фильтрацию" вейвлет-спектра принимаемого сигнала s(t) одновременно в области времени и масштабов (частот) с помощью специального фильтра H(α,τ):

где в качестве масштабно-временного фильтра Н(α,τ) выступает двумерная функция специального вида:

где: Ws(α,τ) - вейвлет-спектр копии излученного сигнала s(t),

А - уровень, задаваемый исходя из условия:

параметр 0<В<1 выбирается в зависимости от вида частотной модуляции сигнала и условия сохранения заданной доли энергии исходного сигнала (E_S1=C·E_S, 0<C<1), приходящейся на восстановленный сигнал s₁(t) после применения обратного ВП к результату перемножения (фильтрации):

Проведенное моделирование (в среде MathCad) предлагаемого метода фильтрации для ЛЧМ-сигнала на фоне гауссового белого шума показало, что при использовании вейвлета Морле (с параметром ω₀=5) для достижения уровня E_S1≈0,99·E_S достаточно выбрать параметр В равным 0.1.

Для пояснения сущности операции формирования масштабно-временной фильтрующей функции (12) и операции фильтрации входного процесса в масштабно-временной области (11) на фиг.1-6 в качестве иллюстрации приведены результаты моделирования (полученные в среде MathCad) предлагаемого метода фильтрации для ЛЧМ-сигнала, обнаруживаемого на фоне гауссового белого шума.

На фиг.1 приведен модуль ВП эталонного ЛЧМ-сигнала.

На фиг.2 приведен вид масштабно-временной фильтрующей функции для ЛЧМ-сигнала.

На фиг.3 приведен модуль ВП входного процесса для гипотезы Н₁: x(t)=s(t)+n(t), где: s(t) - ЛЧМ-сигнал, a n(t) - белый шум.

На фиг.4 показан результат фильтрации (11) ВП входного процесса для гипотезы H₁.

На фиг.5 приведен модуль ВП входного процесса для гипотезы Н₀: x(t)=n(t).

На фиг.6 показан результат фильтрации (11) ВП входного процесса для гипотезы Н₀.

На всех фиг.1-6 в качестве способа визуализации уровней поверхности вейвлет-спектров применена градация яркости (белый цвет - соответствует максимальному уровню, черный - минимальному уровню); по горизонтальной оси отложена шкала временных сдвигов τ, по вертикальной оси - шкала масштабов α.

Предварительная фильтрация (11) входного процесса x(t) в масштабно-временной области (для наиболее широко применяемого в гидролокации и радиолокации класса частотно-модулированных сигналов) позволяет добиться значительного (более 6 дБ) выигрыша в помехоустойчивости по сравнению с прототипом - с классической согласованной фильтрацией или корреляционным приемником [1-5].

Выходное ОСП предлагаемого обнаружителя справедливо записать в виде: , выходное ОСП классической согласованной фильтрации: .

Выигрыш в помехоустойчивости предлагаемого способа обнаружения ЧМС по сравнению с классической согласованной фильтрацией обусловлен уменьшением уровня помех (N₁<N) после "вейвлет-фильтрации" (11) входного процесса при сохранении примерно неизменной энергии принимаемого сигнала (E_S2≈Е_S1) в выходном процессе (при выполнении гипотезы H₁).

Уменьшение уровня спектральной плотности помехи (так же, как и ее дисперсии) и, соответственно, увеличение ОСП (характеризующее выигрыш в помехоустойчивости) примерно равно отношению "площадей" в масштабно-временной области, занимаемых вейвлет-спектром входного процесса до Wx и после Wx₁ "вейвлет-фильтрации":

т.к. в случае белого шума его мощность (после ВП) равномерно распределяется по масштабно-временной области в пределах условного "прямоугольника" (фиг.2), ограниченного по оси времени τ - длительностью импульса Т_S и по оси масштабов α - полосой масштабов Δα_S=α₁-α₂ (однозначно соответствующей спектральной полосе девиации частоты модулированного сигнала Δf_S=f_в-f_н). После фильтрации (11) оставшаяся в выходном процессе x₁(t) часть мощности помехи в масштабно-временной области ограничена площадью носителя фильтрующей функции (α,τ)∈supp{Н(α,τ)}, где Н(α,τ)≠0.

Сущность предлагаемого способа

Предлагаемый способ обнаружения частотно-модулированных сигналов с фильтрацией в масштабно-временной области включает в себя следующие операции:

1. Вычисление вейвлет-преобразования Wx(α,τ) входного процесса x(t) (наиболее эффективно эта процедура реализуется в частотной области с использованием аналитического вейвлета в соответствии с оператором (5)):

1.1. выбор исходного вейвлета ψ(t), вычисление его спектра Фурье , комплексное сопряжение и обнуление отрицательных частот (приведение к аналитическому виду): , при f>0 и, при f≤0 (в случае выбора комплексного аналитического вейвлета последняя процедура - обнуления отрицательных частот необязательна),

1.2. вычисление базиса спектров аналитических вейвлетов путем масштабирования (сжатия) исходного спектра материнского вейвлета: ,

1.3. вычисление спектра Фурье входного процесса ,

1.4. перемножение спектра Фурье входного процесса с сопряженным базисом сжатых спектров аналитических вейвлетов ,

1.5. вычисление обратного преобразования Фурье от результата последнего перемножения: .

2. Вычисление вейвлет-преобразования Ws(α,τ) эталона зондирующего сигнала s(t) (с использованием вычисленного ранее базиса спектров аналитических вейвлетов (в соответствии с п.1.2)):

2.1. вычисление спектра Фурье эталонного сигнала ,

2.2. перемножение спектра Фурье эталонного сигнала с сопряженным базисом сжатых спектров аналитических вейвлетов ,

2.3. вычисление обратного преобразования Фурье от результата последнего перемножения: .

3. Формирование двумерной фильтрующей функции H(α,τ) в масштабно-временной плоскости, вырезающей область значений (α,τ), где модуль комплексного вейвлет-спектра эталона зондирующего сигнала Ws(α,τ) превышает заданный уровень А (13):

4. Перемножение вейвлет-спектра входного процесса и масштабно-временной фильтрующей функции:

Wx₁(α,τ)=Wx(α,τ)·H(α,τ).

5. Вычисление обратного вейвлет-преобразования для результата последнего перемножения Wx₁(α,τ) (с использованием вычисленного ранее базиса спектров аналитических вейвлетов (в соответствии с п.1.2)):

5.1. вычисление прямого преобразования Фурье по τ от двумерного вейвлет-спектра ,

5.2. перемножение спектра Фурье с сопряженным базисом спектров аналитических вейвлетов ,

5.3. вычисление обратного преобразования Фурье по f от результата последнего перемножения: ,

5.4. интегрирование Wx₁'(α,t) по мере (Деление на нормирующий коэффициент С_ψ (3), входящий в состав оператора (6), может не производиться, т.к. это не влияет на помехоустойчивость предлагаемого способа обнаружения. Интегрирование по мультипликативной мере необходимо лишь в случае экспоненциальной дискретизации масштабных коэффициентов вида (7), в случае линейной дискретизации вида (8) достаточно провести интегрирование по обычной аддитивной мере ),

5.5. вычисление реальной части восстановленного процесса Re{x₁(t)} (необходимость данной процедуры обусловлена аналитичностью использованного вейвлета ψ(t) и, соответственно, аналитичностью выходного процесса x₁(t)).

Дальнейшие операции по обработке процесса x₁(t) совпадают с классической реализацией метода обнаружения сигнала известной формы на основе согласованной фильтрации:

6. Согласованная фильтрация обнаруживаемого сигнала s(t) известной формы:

6.1. вычисление комплексного спектра Фурье процесса x₁(t),

6.2. вычисление комплексного спектра Фурье эталонного сигнала s(t) и его комплексное сопряжение ,

6.3. перемножение комплексного спектра Фурье с сопряженным спектром Фурье эталона ,

6.4. вычисление обратного преобразования Фурье от результата последнего перемножения: .

7. Выделение (квадратичное детектирование) огибающей отклика согласованного фильтра: (вычисление квадрата модуля |y(t)|² отклика СФ y(t)).

8. Сравнение |y(t)|² с порогом (выбираемым в зависимости от требуемой вероятности ложной тревоги) и принятие решения об обнаружении сигнала в случае превышения порога (гипотеза H₁), либо о необнаружении - в случае непревышения порога (гипотеза H₀).

Следует отметить, что при использовании огибающей отклика СФ |y(t)|² достаточно наблюдать ее амплитуду через интервал времени, приблизительно равный эффективной ширине полосы огибающей [1, с.343].

Заметим также, что операции 1.1 и 1.2 производятся только с вейвлетом ψ(t), операции 2.1, 2.2, 2.3, 3 и 6.2 производятся только с эталонным сигналом s(t), а не с исследуемым входным процессом x(t), и т.о. данные операции могут быть проведены заранее, а результаты их расчетов - храниться в ПЗУ.

Устройство, реализующее предлагаемый способ

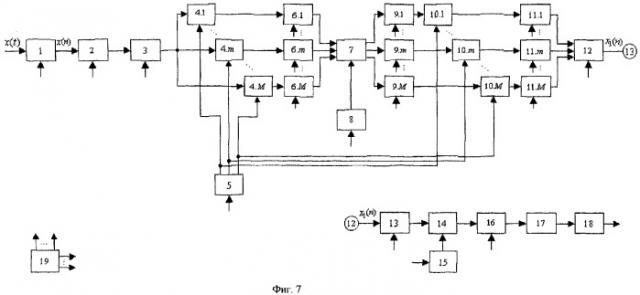
Устройство, реализующее предлагаемый способ обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области, приведено на фиг.7, где:

блок 1 - аналого-цифровой преобразователь (АЦП),

блок 2 - рециркулятор,

блок 3 - вычислитель быстрого преобразования Фурье (БПФ) 1,

блоки 4.1-4.М - комплексные перемножители,

блок 5 - постоянное запоминающее устройство (ПЗУ) 1,

блоки 6.1-6.М - вычислители обратного БПФ,

блок 7 - матричный комплексный перемножитель,

блок 8 - ПЗУ 2,

блоки 9.1-9.М - вычислители БПФ,

блоки 10.1-10.М - комплексные перемножители,

блок 11.1-11.М - вычислители обратного БПФ,

блок 12 - матричный интегратор,

блок 13 - вычислитель БПФ 2,

блок 14 - комплексный перемножитель,

блок 15 - ПЗУ 3,

блок 16 - вычислитель обратного БПФ,

блок 17 - вычислитель квадрата модуля,

блок 18 - пороговое устройство,

блок 19 - управляющее устройство.

Т.о. устройство, реализующее предлагаемый способ, содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, а выход которого соединен с входом рециркулятора (блок 2), выход которого соединен с входом первого вычислителя быстрого преобразования Фурье (блок 3), выход которого соединен с первыми входами М комплексных перемножителей (блоки 4.1-4.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 6.1-6.М), выходы которых соединены с первыми входами матричного комплексного перемножителя (блок 7), выходы которого соединены с входами М вычислителей быстрого преобразования Фурье (блоки 9.1-9.М), выходы которых соединены с первыми входами М комплексных перемножителей (блоки 10.1-10.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 11.1-11.M), выходы которых соединены с входами матричного интегратора (блок 12), выход которого соединен с входом второго вычислителя быстрого преобразования Фурье (блок 13), выход которого соединен с первым входом комплексного перемножителя (блок 14), выход которого соединен с входом вычислителя обратного быстрого преобразования Фурье (блок 16), выход которого соединен с входом вычислителя квадрата модуля (блок 17), выход которого соединен с входом порогового устройства (блок 18), выход которого является выходом устройства; первое постоянное запоминающее устройство (блок 5), выходы которого соединены со вторыми входами М комплексных перемножителей (блоки 4.1-4.М) и со вторыми входами М комплексных перемножителей (блоки 10.1-10.M); второе постоянное запоминающее устройство (блок 8), выход которого соединен со вторым входом матричного комплексного перемножителя (блок 7); третье постоянное запоминающее устройство (блок 15), выход которого соединен со вторым входом комплексного перемножителя (блок 14); управляющее устройство (блок 19), выходы которого соединены с управляющими входами аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителей быстрого преобразования Фурье (блоки 3, 9.1-9.М и 13), комплексных перемножителей (блоки 4.1-4.М, 7, 10.1-10.М и 14), вычислителей обратного быстрого преобразования Фурье (блоки 6.1-6.М, 11.1-11.М и 16) и постоянных запоминающих устройств (блоки 5, 8 и 15).

Принцип действия устройства заключается в следующем. На вход устройства поступает реализация входного процесса x(t), которая поступает на вход АЦП (блок 1) с частотой дискретизации, удовлетворяющей требованиям теоремы Котельникова:

С выхода АЦП (блок 1) дискретные отсчеты поступают на вход рециркулятора (блок 2), где формируется и с каждым новым отсчетом обновляется текущая дискретная выборка х(n) длиной N отсчетов. Длина выборки N определяется длительностью излучаемого сигнала и интервалом дискретизации: . Сформированная текущая дискретная выборка входного процесса x(n) поступает на вход первого вычислителя БПФ (блок 3), с выхода которого комплексный спектр входной реализации поступает одновременно на первые входы М комплексных перемножителей (блоки 4.1-4.М).

С выходов первого ПЗУ (блок 5) считывается М одномерных массивов длиной N отсчетов (вычисленного заранее базиса сжатых спектров аналитических вейвлетов) и поступает на вторые входы комплексных перемножителей (блоки 4.1-4.М), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 6.1-6.М). Количество масштабов М определяется максимальным значением коэффициента сжатия исходного вейвлета α_max и шагом линейной дискретизации масштаба .

С выходов вычислителей обратного БПФ (блоки 6.1-6.М) результат вейвлет-преобразования входного процесса Wx(m,n) в виде двумерного массива размером М масштабов на N сдвигов поступает на первые входы матричного комплексного перемножителя (блок 7).

С выхода второго ПЗУ (блок 8) считывается вычисленный заранее двумерный массив фильтрующей функции Н(m,n) (в масштабно-временной плоскости) размером М масштабов на N сдвигов и поступает на второй вход матричного комплексного перемножителя (блок 7), с выходов которого M одномерных массивов длиной N отсчетов результата перемножения (т.е. фильтрации в масштабно-временной плоскости) Wx₁(m,n) поступают на входы вычислителей БПФ (блоки 9.1-9.М), с выходов которых результаты БПФ поступают на первые входы М комплексных перемножителей (блоки 10.1 -10.М).

С выходов первого ПЗУ (блок 5) считывается М одномерных массивов длиной N отсчетов (вычисленного заранее базиса сжатых спектров аналитических вейвлетов) и поступает на вторые входы комплексных перемножителей (блоки 10.1-10.М), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 11.1-11.М), с выходов которых результаты обратного БПФ Wx₁'(m,n) поступают на входы матричного интегратора (блок 12), где производится интегральное суммирование Wx₁'(m,n) масштабом m.

С выхода матричного интегратора (блок 12) временная реализация отфильтрованного в масштабно-временной области процесса х₁(n) поступает на вход второго вычислителя БПФ (блок 13), с выхода которого комплексный спектр поступает на первый вход комплексного перемножителя (блок 14).

Из третьего ПЗУ (блок 15) считывается вычисленный заранее сопряженный комплексный спектр эталонного сигнала и поступает на второй вход комплексного перемножителя (блок 14), с выхода которого результат перемножения поступает на вход вычислителя обратного БПФ (блок 16). С выхода вычислителя обратного БПФ (блок 16) отклик согласованного фильтра y(n) поступает на вход вычислителя квадрата модуля (блок 17), с выхода которого выделенная огибающая |y(n)|² поступает на вход порогового устройства (блок 18), выход которого является выходом устройства.

Устройство управления (блок 19) осуществляет синхронизацию работы: аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителей быстрого преобразования Фурье (блоки 3, 9.1-9.М и 13), комплексных перемножителей (блоки 4.1-4.М, 7, 10.1-10.М и 14), вычислителей обратного быстрого преобразования Фурье (блоки 6.1-6.М, 11.1-11.М и 16) и постоянных запоминающих устройств (блоки 5, 8 и 15).

Список использованных источников

1. Бурдик B.C. Анализ гидроакустических систем. Л.: Судостроение, 1988, 392 с. (Прототип, с.339-343).

2. Лезин Ю.С. Введение в теорию и технику радиотехнических систем. М.: Радио и связь, 1986, 280 с.

3. Хелстром К. Статистическая теория обнаружения сигналов. М.: Иностранная литература, 1963, 430 с.

4. Ван-Трис Г. Теория обнаружения, оценок и модуляции, т.1, М.: Сов. радио, 1972, 744 с.

5. Ван-Трис Г. Теория обнаружения, оценок и модуляции, т.3, М.: Сов. радио, 1977, 661 с.

6. Добеши И. Десять лекций по вейвлетам. Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001, 464 с.

7. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения. Успехи физических наук. Том 166, №11, 1996, с.1145-1170.

8. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование. Успехи физических наук. Том 171, №5, 2001, с.465-501.

9. Дьяконов В.П. Вейвлеты. От теории к практике. М.: СОЛОН-Р, 2002, 440 с.

10. Кравченко В.Ф., Рвачев В.А. "Wavelet"-системы и их применение в обработке сигналов. Зарубежная радиоэлектроника. 1996, №4, с.3-20.

11. Коэн Л. Время-частотные распределения: Обзор. ТИИЭР, 1989, т.77, №10, с.72-120.

12. Сапрыкин В.А., Малый В.В., Лопухин Р.В. "Способ и устройство быстрого вычисления дискретного вейвлет-преобразования сигнала с произвольным шагом дискретизации масштабных коэффициентов". Описание изобретения по заявке №2003100794/09(000537) от 09.01.2003 г. Положительное решение о выдаче патента от 23.09.2004 г.

1. Способ обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области, основанный на согласованной фильтрации принятого сигнала и заключающийся в вычислении комплексного спектра прямого преобразования Фурье входного сигнала, вычислении комплексного спектра прямого преобразования Фурье копии излученного сигнала и его комплексного сопряжения, перемножении комплексного спектра прямого преобразования Фурье входного сигнала с сопряженным спектром прямого преобразования Фурье копии излученного сигнала, вычислении обратного преобразования Фурье от результата перемножения, вычислении квадрата модуля, сравнении с порогом, выбираемым в зависимости от требуемой вероятности ложной тревоги, и принятии решения об обнаружении сигнала в случае превышения порога, отличающийся тем, что перед согласованной фильтрацией проводят предварительную фильтрацию принятого входного сигнала в масштабно-временной области путем вычисления прямого вейвлет-преобразования принятого входного сигнала, вычисления прямого вейвлет-преобразования копии излученного сигнала, формирования двумерной фильтрующей функции в масштабно-временной плоскости, вырезающей область значений, где модуль комплексного вейвлет-спектра копии излученного сигнала превышает заданный уровень, перемножения вейвлет-спектра принятого входного сигнала и масштабно-временной двумерной фильтрующей функции, вычисления обратного вейвлет-преобразования результата последнего перемножения, с последующей дальнейшей обработкой результата вычисления обратного вейвлет-преобразования на основе согласованной фильтрации.

2. Устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области, содержащее аналого-цифровой преобразователь (1), на вход которого подается входной сигнал, выход аналого-цифрового преобразователя соединен с входом рециркулятора (2), выход которого соединен с входом первого вычислителя быстрого преобразования Фурье (3), отличающееся тем, что выход первого вычислителя быстрого преобразования Фурье (3) соединен с первыми входами М комплексных перемножителей (4.1-4.М), выходы которых соединены с входами М вычислителей обратного быстрого преобразования Фурье (6.1-6.М), выходы которых соединены с первыми входами матричного комплексного перемножителя (7), выходы которого соединены с входами М вычислителей быстрого преобразования Фурье (9.1-9.М), выходы которых соединены с первыми входами М комплексных перемножителей (10.1-10.М), выходы которых соединены с входами М вычислителей обратного быстрого преобразования Фурье (11.1-11.М), выходы которых соединены с входами матричного интегратора (12), выход которого соединен с входом второго вычислителя быстрого преобразования Фурье (13), выход которого соединен с первым входом комплексного перемножителя (14), выход которого соединен с входом вычислителя обратного быстрого преобразования Фурье (16), выход которого соединен с входом вычислителя квадрата модуля (17), выход которого соединен с входом порогового устройства (18), выход которого является выходом устройства, при этом выходы первого постоянного запоминающего устройства (5) соединены со вторыми входами М комплексных перемножителей (4.1-4.М) и со вторыми входами М комплексных перемножителей (10.1-10.М), выход второго постоянного запоминающего устройства (8) соединен со вторым входом матричного комплексного перемножителя (7), выход третьего постоянного запоминающего устройства (15) соединен со вторым входом комплексного перемножителя (14), выходы управляющего устройства (19) соединены с управляющими входами аналого-цифрового преобразователя (1), рециркулятора (2), вычислителей быстрого преобразования Фурье (3.9.1-9.М и 13), комплексных перемножителей (4.1-4.М, 7, 10.1-10.М и 14), вычислителей обратного быстрого преобразования Фурье (6.1-6.М, 11.1-11.М и 16) и постоянных запоминающих устройств (5, 8, 15).