Способ выравнивания решетки узлов в соответствии с характерными чертами в цифровом изображении

Способ выравнивания решетки узлов в соответствии с характерными чертами в цифровом изображении

Иллюстрации

Показать все

Реферат

Данное изобретение относится к анализу цифровых изображений, а в особенности к конструированию вычислительных сеток из таких изображений.

Описание предшествующего уровня техники

Цифровые изображения часто анализируют, чтобы получить сетки для дальнейших вычислений. К примеру, сейсмические изображения анализируют, чтобы получить геологические сетки, используемые для моделирования нефти, текущей в подземных резервуарах. Аналогично, медицинские изображения человеческого мозга анализируют, чтобы получить сетки, используемые для моделирования кровотока в артериях. Несколько иным примером является морфинг, т.е. преобразование изображений, при котором сетки, выделенные из одного изображения, могут использоваться для эффективного кодирования различий в последующих изображениях. Во всех этих применениях изображение анализируют для конструирования сетки.

Изображения и построение сеток сегодня

Характерно, что такие применения часто состоят из следующей последовательности этапов:

(1) Обрабатывают изображение, чтобы усилить вызывающие интерес характерные черты.

(2) Находят кривые или поверхности в изображениях, которые ограничивают вызывающие интерес области.

(3) Заполняют пространство, определенное этими областями, вычислительной сеткой.

(4) Моделируют некий процесс на заполняющей пространство сетке.

Для применения к медицинским изображениям см. Cebral, J.R., and Luhner, R., From Medical Images to CFD Meshes, Proceedings of the 8th International Meshing Roundtable, p.321-331, Sandia, 1999. Для применения к сейсмическим изображениям см. Garrett, S., Griesbach, S., Johnson, D., Jones, D., Lo, M., Orr, W., and Sword, C., Earth Model Synthesis, First Break, v.l5, no.1, p.13-20, 1997.

По разным причинам каждый этап в этой последовательности сегодня часто выполняют независимо, с малым вниманием к требованиям последующих шагов. Например, общепринято на этапе (2) вырабатывать ограничивающие кривые или поверхности с бульшим числом деталей, чем может быть представлено используемой на этапе (4) заполняющей пространство сеткой. По обыкновению сейсмические отражения, представляющие геологические пограничные слои, отображают с более высоким разрешением, чем можно практически использовать в сетках для моделирования нефтяных резервуаров. Это ведет к проблеме "перемасштабирования", указанной Garrett et al. (1997).

Это расхождение в разрешении часто сопровождается расхождением в структуре данных. К примеру, двумерная кривая, представленная простым связанным списком линейных сегментов на этапе (2), может стать относительно сложной сеткой треугольников на этапе (3). Такие расхождения сегодня подрывают последовательность анализа и могут привести к несоответствиям между изображением, обработанным на этапе (1), и сеткой, используемой на этапе (4), которые трудно оценить количественно.

Расхождения эти дорогостоящи. В примере с анализом сейсмических изображений одна итерация данной последовательности сегодня может потребовать месяцев работы. Эта высокая стоимость затрудняет выполнение множества итераций при попытке оценить неопределенности в результатах анализа.

Одна причина расхождений в разрешении и структуре данных лежит в реализации последовательности анализа. Исторически перечисленные выше четыре этапа могут выполняться отдельными компьютерными программами, разработанными независимо и используемыми разными специалистами. В настоящее время все четыре этапа в данной последовательности может выполнять один человек или небольшая группа, и имеется потребность, чтобы эти этапы были объединены в большей степени.

Другой причиной расхождений является отсутствие методики. Этап (4) моделирования часто требует численного решения дифференциальных уравнений в частных производных (ДУЧП, PDEs). В прошлом эти решения были осуществимы только для структурированных сеток, в которых элементы могут быть проиндексированы как простые массивы. Преобразование неструктурированной сетки, выработанной на этапе (3), в структурированную сетку создает дополнительные несоответствия между обработанным изображением и сеткой, используемой в моделировании. Однако недавние достижения в численных методах решения ДУЧП на неструктурированных сетках подсказывают, что этого преобразования и получающихся несоответствий можно избежать.

Формирование сеток с помощью решеток

Точность большинства вычислений, выполняемых на сетках, зависит от регулярности сеточных элементов. Моделирование, выполненное на треугольных сетках с высокой регулярностью, имеющих почти равносторонние треугольники, является более точным, чем то, которое выполнено на нерегулярных сетках с длинными тонкими треугольниками.

Это одна причина, по которой популярна триангуляция Делонэ. При заданном наборе узлов, представляющих местоположения узлов для двумерной сетки, триангуляция Делонэ этих узлов по сравнению со всеми иными возможными триангуляциями дает треугольники, в наибольшей степени близкие к равносторонним. Однако триангуляция Делонэ сама по себе не гарантирует регулярной сетки. Для этого необходимо тщательно выбирать местоположения узлов сетки.

(Для обзора двумерной и трехмерной триангуляции Делонэ в применении к проблеме построения сеток см. Bern, М., and Eppstein, D., Mesh Generation and Optimal Triangulation, in Computing in Euclidean Geometry, Du, D.-Z. and Hwang, F.K. eds., World Scientific, 1995.)

За рамками области анализа изображений проблема выбора оптимальных расположений сеточных узлов изучена хорошо. Одно решение для этой проблемы основано на наблюдении, что триангуляция набора узлов, определенного простой кристаллической решеткой, дает сетку с высокой регулярностью. (См. Mello, U.T., and Cavalcanti, P.R., A Point Creation Strategy for Mesh Generation Using Crystal Lattices as Templates, Proceedings of the 9th International Meshing Roundtable, p.253-261, Sandia, 2000.) Однако равномерная решетка узлов может лишь в редких случаях совмещаться с границами объектов, для которых нужно получить сетки. Поэтому некоторые решения начинаются с приблизительно равномерной решетки, а затем используются численные модели физических сил между атомами или пузырьками для автоматического перемещения сеточных узлов (атомов или пузырьков) в более оптимальные местоположения. (См. Shimada, К., Physically-Based Mesh Generation: Automated Triangulation of Surfaces and Volumes via Bubble Packing, Ph.D. thesis, Massachusetts Institute of Technology, 1993, и Shimada, К., and Gossard, D.C., Bubble Mesh: Automated Triangular Meshing of Non-Manifold Geometry by Sphere Packing, в Proceedings of the Third Symposium on Solid Modeling and Applications, p.409-419. Патент США №6124857 на имя Itoh, Т., Inoue, К., Yamada, A., and Shimada, K., Meshing Method and Apparatus, 2000, расширяет эту работу на получение сеток из четырехугольников. (См. Bossen, F.J., and Heckbert, P.S., A Plant Method for Anisotropic Mesh Generation, Proceedings of the 5th International Meshing Roundtable, p.63-74, Sandia, 1996.)

Во всех этих примерах получение сетки на основе решетки начинается с геометрической модели, которая точно определяет внутренние и наружные границы объектов, для которых строятся сетки. Таким образом, существует необходимость в системе и методике построения сеток, способных решить проблемы, где такие границы неизвестны заранее.

Патенты США, указанные в этом описании

4908781 на имя Levinthal, С., and Fine, R., Computing Device for Calculating Energy and Pairwise Central Forces of Particle Interactions, 1990.

5596511 на имя Toyoda, S., Ikeda, H., Hashimoto, E., and Miyakawa, N., Computing Method and Apparatus for a Many-Body Problem, 1997.

6124857 на имя Itoh, Т., Inoue, К., Yamada, A., and Shimada, K., Meshing Method and Apparatus, 2000.

Другие ссылки, указанные в данном описании

Bentley, J.L., and Friedman, J.H., Data Structures for Range Searching, Computing Surveys, Vol.11, no.4, 1979.

Bern, M., and Eppstein, D., Mesh Generation and Optimal Triangulation, в Computing in Euclidean Geometry, Du, D.-Z. and Hwang, F.K. eds., World Scientific, 1995.

Bossen, F.J., and Heckbert, P.S., A Plant Method for Anisotropic Mesh Generation, Proceedings of the 5th International Meshing Roundtable, p.63-74, Sandia, 1996.

Byrd, R.H., Nocedal, J., and Schnabel, R.B., Representations of Quasi-Newton Matrices and Their Use in Limited Memory Methods, Technical Report NAM-03, Northwestern University, Department of Electrical Engineering and Computer Science, 1996.

Cebral, J.R., and Luhner, R., From Medical Images to CFD Meshes, Proceedings of the 8th International Meshing Roundtable, p.321-331, Sandia, 1999.

Garrett, S., Griesbach, S., Johnson, D., Jones, D., Lo, M., Orr, W., and Sword, C., Earth Model Synthesis, First Break, v.15, no.1, p.13-20, 1997.

Mello, U.T., and Cavalcanti, P.R., A Point Creation Strategy for Mesh Generation Using Crystal Lattices as Templates, Proceedings of the 9th International Meshing Roundtable, p.253-261, Sandia, 2000.

Shimada, K., Physically-Based Mesh Generation: Automated Triangulation of Surfaces and Volumes via Bubble Packing, Ph.D. thesis, Massachusetts Institute of Technology, 1993.

Shimada, K., and Gossard, D.C., Bubble Mesh: Automated Triangular Meshing of Non-Manifold Geometry by Sphere Packing, в Proceedings of the Third Symposium on Solid Modeling and Applications, p.409-419, 1995.

Сущность изобретения

В соответствии с различными вариантами осуществления данного изобретения способ генерирования решетки узлов по отношению к характерным чертам в цифровом изображении содержит процесс инициализации решетки и процесс оптимизации совмещения этой решетки по отношению к характерным чертам изображения. Процесс оптимизации работает путем корректирования узлов решетки с целью получения экстремума составной функции пространственных координат узлов решетки. Составная функция может быть взвешенной комбинацией первой функции попарных расстояний между узлами и второй функции, выделенной из изображения (например, вычисленной из выборок изображения вблизи узлов решетки).

Из оптимизированной решетки может генерироваться сетка. Эта сетка может использоваться в любом из множества применений. К примеру, сетка может использоваться для моделирования процесса, связанного с изображением. В качестве другого примера, сетка может использоваться для сжатия изображения или последующих изображений в последовательности изображений (например, в видеопотоке).

В некоторых вариантах осуществления оптимизированная решетка может использоваться для кодирования информации, связанной с изображением, с генерированием или без генерирования промежуточной сетки. Предполагается любой из различных типов связанной информации.

Задачи и преимущества

Одной задачей по меньшей мере некоторых вариантов осуществления данного изобретения является способ, который позволяет заменить описанную выше (при описании предшествующего уровня техники) последовательность анализа изображений более эффективной последовательностью:

(1) Обрабатывают изображение, чтобы усилить вызывающие интерес характерные черты.

(2) Заполняют пространство вычислительной сеткой, совмещенной характерными чертами с характерными чертами изображения.

(3) Моделируют некий процесс на заполняющей пространство сетке.

Вместо нахождения границ областей в изображениях, а затем построения сеток в этих областях, просто конструируют сетку, которая совмещается с границами.

Дополнительными задачами некоторых вариантов осуществления данного изобретения являются использование данного способа для построения:

- сеток с высокой регулярностью, пригодных для дальнейших вычислений, таких как решение дифференциальных уравнений в частных производных; и

- градуированных сеток, в которых плотность сеточных узлов изменяется в зависимости от сложности изображения или как функция, определенная пользователем; и

- трехмерных сеток, где доступны трехмерные изображения.

Эти и другие задачи и преимущества разных вариантов осуществления изобретения станут понятны из рассмотрения нижеследующего описания и чертежей.

Перечень чертежей

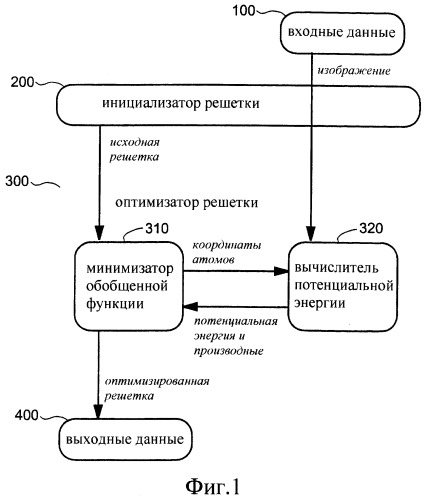
Фиг.1 - поток данных среди первичных компонентов в способе по данному изобретению.

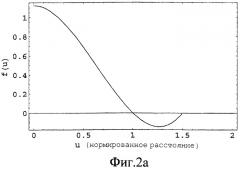
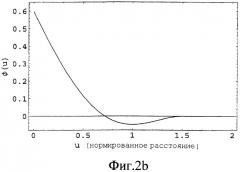
Фиг.2 - двухточечные функции силы (фиг.2а) и потенциала (фиг.2b) от нормированного расстояния между любыми двумя атомами.

Фиг.3 - вклады для номинальных расстояний 4 (фиг.3а) и 8 (фиг.3b) одного атома в дискретное поле потенциалов атомов.

Фиг.4 - гексагональная двумерная решетка атомов, которую триангулировали.

Фиг.5 - гранецентрированная спереди кубическая трехмерная решетка атомов.

Фиг.6 - сейсмическое изображение, которое обработано, чтобы усилить дефекты, разрывы в подземной геологии.

Фиг.7 - функция номинального расстояния, которая представляет желаемый переменный промежуток между атомами в решетке.

Фиг.8 - начальное псевдорегулярное распределение атомов в решетке; каждый атом помечен кружком с диаметром, пропорциональным функции номинального расстояния, оцененной в местоположении атома.

Фиг.9 - сетка, соответствующая псевдорегулярной исходной решетке для сейсмического изображения.

Фиг.10 - сетка, соответствующая псевдослучайной исходной решетке для сейсмического изображения.

Фиг.11 - сетка, соответствующая оптимизированной решетке для сейсмического изображения.

Фиг.12 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в сейсмическом изображении.

Фиг.13 - сетка Вороного, соответствующая оптимизированной решетке, в которой атомы отталкиваются характерными чертами в сейсмическом изображении.

Фиг.14 - магниторезонансное изображение (МРИ, MRI) человеческой головы.

Фиг.15 - изображение человеческой головы, обработанное для усиления краевых характерных черт.

Фиг.16 - сетка, совмещенная с характерными чертами изображения человеческой головы.

Фиг.17 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в изображении человеческой головы.

Фиг.18 - магниторезонансное изображение (МРИ) человеческого торса.

Фиг.19 - изображение человеческого торса, обработанное для усиления краевых признаков.

Фиг.20 - сетка, совмещенная с характерными чертами изображения человеческого торса.

Фиг.21 - края в сетке, которые в наибольшей степени совмещаются с характерными чертами в изображении человеческого торса.

Фиг.22 - компоненты вычислительного устройства, использованные для реализации способа по данному изобретению.

Фиг.23 - вариант осуществления способа по данному изобретению.

Хотя изобретение допускает различные модификации и альтернативные формы, конкретные варианты его осуществления показаны посредством примеров на чертежах и будут здесь описаны подробно. Следует понимать, однако, что чертежи и их подробное описание не предназначены для ограничения изобретения раскрытыми конкретными формами, но напротив, изобретение охватывает все модификации, эквиваленты и альтернативные варианты, отвечающие сущности и объему настоящего изобретения, как оно определено приложенной формулой изобретения.

Подробное описание предпочтительных вариантов осуществления

Здесь описывается способ генерирования решетки узлов, который учитывает характерные черты в цифровом изображении. Этот способ содержит инициализацию, а затем оптимизацию решетки узлов. В одном наборе вариантов осуществления узлы оптимизированной решетки стремятся совместиться (совпасть) с характерными чертами в изображении. Во втором наборе вариантов осуществления узлы оптимизированной решетки стремятся выстроиться вблизи характерных черт в изображении, но не совпасть с ними. В других вариантах осуществления узлы оптимизированной решетки могут стремиться совместиться с некоторыми характерными чертами и не совместиться с другими характерными чертами в том же самом изображении.

Здесь и далее заявители называют узлы решетки атомами. Заявители описывают процесс инициализации решетки в терминах атомных структур кристаллов. Подобным же образом они описывают оптимизацию решетки в терминах минимизации потенциальной энергии атомной решетки. Эти физические модели делают данное описание более легким для понимания, но атом в контексте данного изобретения является просто узлом.

Фиг.1 иллюстрирует более подробно поток данных между первичными компонентами данного способа. Компонент 100 ввода данных вырабатывает изображение, которое обрабатывают где-то в другом месте для выделения вызывающих интерес характерных черт. Здесь изображение либо получают непосредственно как результат этой обработки, либо загружают из компьютерной памяти. Инициализатор 200 решетки создает исходную решетку атомов, которая охватывает изображение. Оптимизатор 300 решетки перемещает атомы так, чтобы решетка совместилась с характерными чертами в изображении. Компонент 400 вывода данных потребляет оптимизированную решетку атомов, либо передавая ее на какую-то иную обработку, либо сохраняя ее в компьютерной памяти.

Оптимизатор 300 решетки содержит минимизатор 310 порождающей функции и вычислитель 320 потенциальной энергии. Минимизатор 310 обобщенной функции итеративно ищет минимум функции многих переменных. Во время этого поиска данный минимизатор требует повторных оценок данной функции и ее частных производных по каждой переменной. Здесь переменными являются пространственные координаты атомов в решетке. При заданных координатах атомов и изображении вычислитель 320 потенциальной энергии оценивает потенциальную энергию решетки и частную производную этой энергии по координате каждого атома.

Вычисление потенциальной энергии

Атом в двумерном пространстве имеет координаты x и y, а атом в трехмерном пространстве имеет координаты x, y и z. Вектор х обозначает пространственные координаты x и y (или x, y и z) узла в двумерном (или трехмерном) пространстве. Пусть заданы два атома с местоположениями x_i и x_j, тогда выражение |x_i-x_j| обозначает расстояние между ними. В предпочтительном варианте осуществления норма |·| вектора, используемая для вычисления этого межатомного расстояния, является эвклидовой нормой. Однако вместо нее может использоваться любая из множества других норм.

Двухточечные потенциальные функции

Для эффективности вычислений заявители моделируют взаимодействие между атомами с помощью простой двухточечной силовой функции, такой, что полная сила, прикладываемая к атому его соседями, является просто суммой сил, прикладываемых каждым из них. Даже при этом упрощении имеется много обоснованных вариантов выбора для двухточечной силовой функции.

Чтобы избежать ситуации, когда два или более атомов имеют те же самые или почти те же самые координаты, сила между ними может быть отталкивающей (положительной), если они находятся слишком близко друг к другу. Аналогично, чтобы предотвратить большие пустые пространства без атомов, сила между двумя атомами может быть притягивающей (отрицательной), если они находятся слишком далеко друг от друга. Для облегчения численных вычислений эта сила может быть ограничена. Для предотвращения того, чтобы каждый атом в решетке воздействовал на каждый другой атом с некоторой силой, эта сила может быть нулевой за пределами расстояния отсечки. Далее, силовая функция может быть непрерывной как функция межатомного расстояния. Силовая функция, предложенная Shimada (1993), имеет эти свойства. Таким образом, в одном наборе вариантов осуществления заявители используют силовую функцию Симада, что описано ниже. Однако можно применять любую из множества силовых функций, соответствующих этим свойствам.

Пусть d обозначает номинальное расстояние между двумя атомами, т.е. расстояние, на котором сила переходит от отталкивающей к притягивающей. Тогда сила f между двумя атомами, расположенными в x_i и x_j, может быть задана кубическим полиномом:

где u - нормированное расстояние между двумя атомами, определяемое выражением

Коэффициенты этой полиномиальной функции гарантируют, что сила ограниченна и непрерывна, что она равна нулю при u=1 и , и что она положительна для 0≤u<1 и отрицательна для . Фиг.2а иллюстрирует эту силовую функцию.

Вообще, сила, действующая на атом, является вектором. Здесь направление этого вектора определяется знаком f(u) и местоположениями x_i и х_j, двух атомов.

Более удобно работать со скалярным потенциалом, чем со множеством компонентов вектора силы. Поэтому, следуя общеизвестному соглашению, заявители определяют силу как градиент скалярного потенциала, взятый со знаком "минус":

Постоянная интегрирования выбрана так, чтобы φ(u) была непрерывна при . Фиг.2b иллюстрирует эту потенциальную функцию. Как ожидается, потенциальная функция φ(u) имеет минимум на нормированном расстоянии u=1, где силовая функция f(u) равна нулю.

Потенциальные энергии и потенциальные поля

При заданной потенциальной функции φ(u) от нормированного расстояния и заявители определяют потенциальную энергию атомов следующей суммой потенциалов попарного взаимодействия:

где x₁, x₂, ..., x_n являются координатами n атомов в решетке, а d(x) - функция номинального межатомного расстояния от положения х. Функция d(x) номинального расстояния не обязательно должна быть постоянной; но чтобы гарантировать гладко изменяющуюся решетку, заявители требуют, чтобы она была гладкой. Конкретно, они требуют, чтобы |▿d|≪1, так что d(x_i)≈d(x_j) для |x_i-x_j|/d меньше, чем расстояние ³/₂ отсечки потенциальной функции φ(u). Далее, множитель 1/2 компенсирует появление φ[|x_i-x_j|/d(x_j)]≈φ[|x_i-x_j|/d(x_i)] дважды в определении полной потенциальной энергии А.

Можно также определить потенциальную энергию А атомов в терминах потенциального поля атомов:

так что

Иными словами, потенциальная энергия атомов определяется как половина суммы значений, полученных оцениванием потенциального поля атомов в координатах атомов.

Аналогично, определяют потенциальную энергию изображения:

где b(x) - потенциальное поле изображения, основанное на входном изображении.

Во многих контекстах потенциальное поле изображения представляет собой просто изображение (или сглаженный вариант изображения), обычно представленный двумерным (или трехмерным) массивом чисел, хранящимся в компьютерной памяти. Здесь заявители используют термин "потенциальное поле", чтобы подчеркнуть (а позже применить) сходство между потенциальными полями атомов и изображения.

В одном наборе вариантов осуществления предполагается, что изображение обработано так, что потенциальное поле изображения достигает минимального значения (например, b(x)≈-1) в пределах вызывающих интерес характерных черт и максимального значения (например, b(x)≈0) в не вызывающих интерес областях. В этом случае минимизация потенциальной энергии В изображения эквивалентна перемещению атомов в минимумы, соответствующие вызывающим интерес характерным чертам в изображении.

Во втором наборе вариантов осуществления предполагается, что изображение обработано так, что потенциальное поле изображения достигает максимального значения (например, b(x)≈1) в пределах вызывающих интерес характерных черт и минимального значения (например, b(x)≈0) в не вызывающих интерес областях. В этом случае минимизация потенциальной энергии В изображения эквивалентна перемещению атомов в максимумы, соответствующие вызывающим интерес характерным чертам в изображении.

В третьем наборе вариантов осуществления потенциальное поле изображения может достигать максимального значения (например, b(х)≈1) вдоль первого поднабора характерных черт изображения, минимального значения (например, b(x)≈-1) вдоль второго поднабора характерных черт изображения и промежуточного значения (например, b(x)≈0) вне этих характерных черт изображения.

В более общем виде заявители перемещают атомы с целью минимизации следующей взвешенной суммы потенциальных энергий атомов и изображения:

которую называют полной потенциальной энергией. Масштабирующий множитель β определяет относительные вклады А и В в полную потенциальную энергию Р. Когда β=0, атомы стремятся к совершенно регулярной решетке, которая не совмещена с изображением. Когда β=1, атомы восприимчивы только к значениям выборок изображения; т.е. атомы перемещаются только на основании их притяжения к минимумам в изображении и/или их отталкивания от максимумов в изображении. Таким образом, атомы стремятся скапливаться в минимумах и освобождать максимумы в изображении, давая очень нерегулярную решетку. Обычно выбирают и получаем решетку, которая приблизительно регулярна и учитывает характерные черты изображения.

В терминах потенциальных полей а(х) и b(х) полная потенциальная энергия составляет:

В терминах полного потенциального поля, определенного как

полная потенциальная энергия равна

Как и для функции d(x) номинального расстояния, масштабирующий множитель β в уравнениях (5) и (6) может быть гладко изменяющейся функцией от положения х. (Что касается d(x), гладкость подразумевает, что производные от β(х) пренебрежимо малы.) Это обобщение обеспечивает баланс между регулярностью решетки и ее восприимчивостью (т.е. притяжением к или отталкиванием от) к пространственно меняющимся характерным чертам изображения. Восприимчивость решетки к характерным чертам изображения может быть важнее в одной части изображения, нежели в какой-либо иной его части. Для простоты заявители определяют здесь β как постоянный масштабирующий множитель.

Полная потенциальная энергия Р является неквадратичной функцией от координат x₁, x₂, ..., х_n атомов со множеством локальных минимумов. (К примеру, отметим, что взаимное изменение координат любых двух атомов не меняет Р.) Поэтому любой поиск минимума, обычно близкого к координатам исходной решетки, должен быть итеративным. При эффективном итеративном поиске нужно неоднократно оценивать частные производные от Р по отношению к координатам атомов. Рассмотрим, к примеру, изменение в Р по отношению к х-координате i-го атома:

При оценивании частной производной ∂А/∂х_i потенциальной энергии атомов вспоминают, что выражение φ[|x_i-x_j|/d(x_j)]≈φ[|x_i-x_j|/d(x_i)] появляется дважды в двойной сумме уравнения (1).

Поэтому,

Аналогичные результаты можно легко получить для частных производных по координате у (а для трехмерного случая - z) - каждого атома.

Вычисление

Вычисление полной потенциальной энергии Р требует вычисления ее компонентов А и В. Чтобы вычислить потенциальную энергию В изображения согласно уравнению (3), нужно оценить потенциальное поле b(х) изображения для местоположения х=x_i каждого атома. Изображения обычно дискретизируют равномерно, и простейшим и наиболее эффективным приближением к b(x_i) является значение потенциального поля b(х) изображения в выборке изображения, ближайшей к узлу x_i. Возможны и более точные приближения (интерполяции), но заявители использовали эту простую и быструю интерполяцию к ближайшему соседу во всех показанных здесь примерах. Уравнение (3) предполагает, что стоимость (вычислительная сложность) вычисления В - О(n), где n - число атомов.

Наоборот, двойная сумма в уравнении (1) предполагает, что стоимость наиболее прямого метода вычисления А составляет O(n²). В практических применениях n достаточно велико, так что стоимость O(n²) вычисления А становится много больше, чем стоимость O(n) оценивания В. Для снижения стоимости вычисления А можно применить представленную конструкцию потенциальной функции φ(u), которая равна нулю для нормированных расстояний и больших, чем расстояние отсечки. Только атомы, ближайшие к атому, расположенному в положении х=х_i, вносят вклад в потенциальное поле a(x_i) атомов в этом положении.

Это замечание приведет к задаче определения того, какие атомы-соседи находятся в пределах расстояния от каждого атома, расположенного в x=x_i. Решение этой задачи нетривиальное, потому что атомы перемещаются неоднократно во время оптимизации решетки.

К примеру, если формируют списки соседних атомов, по одному списку для каждого атома, нужно обновлять эти списки (или по меньшей мере проверять, не требуют ли они обновления) при любых перемещениях атомов. Для решеток с плотностью, близкой к постоянной, стоимость формирования и обновления таких списков, использующих простые структуры данных, представляет собой O(mn), где m - среднее число соседних атомов в пределах расстояния отсечки. Для решеток с переменной плотностью требуются более сложные структуры данных, и стоимость становится O(mnlogn). (См., например, Bentley, J.L., and Friedman, J.H., Data Structures for Range Searching, Computing Surveys, Vol.11, no.4, 1979. См. также патент США №4908781 на имя Levinthal, С., and Fine, R., Computing Device for Calculating Energy and Pairwise Central Forces of Particle Interactions, 1990, и патент США №5596511 на имя Toyoda, S., Ikeda, H., Hashimoto, E., and Miyakawa, N., Computing Method and Apparatus for a Many-Body Problem, 1997.)

Представленное выражение для потенциальной энергии А атомов в терминах потенциального поля а(х) атомов предлагает более простое решение. Заявители интерпретируют уравнение (2) как рецепт для вычисления потенциального поля а(х) атомов, которое дискретизируют подобно потенциальному полю b(х) изображения. Конкретно, представляют а(х) с помощью двумерного или трехмерного массива, имеющего те же самые размерности, что и массив, использованный для представления изображения h(x). Сначала инициализируют а(х) нулем для всего дискретного набора х. Затем для каждого атома, расположенного в положении х=х_j, суммируют нарастающим итогом дискретизированную потенциальную функцию φ[|x-x_j|/d(x_j)]. Это суммирование нарастающим итогом ограничивается пространственно до выборок внутри круга (или сферы) радиуса с центром в положении х_j, где вклад дискретизированной потенциальной функции ненулевой.

Фиг.3а и 3b иллюстрируют две такие потенциальные функции для номинальных расстояний d=4 и d=8 соответственно. Уровни серого между черным и белым соответствуют значениям дискретизированной функции между -0,05 и 0,05 соответственно. Потенциальное поле а(х) атомов представляет собой просто результат суммирования нарастающим итогом множества таких функций. Для вычислительной эффективности эти дискретизированные потенциальные функции могут быть заранее вычислены и затабулированы для различных номинальных расстояний d. Затем, задавая d(x) для любого местоположения х, соответствующие значения потенциальной функции можно эффективно определить путем табличного просмотра (или путем табличного просмотра и интерполяции).

Предпочтительный вариант осуществления

Представленный анализ предлагает два совершенно разных алгоритма для вычисления полной потенциальной энергии и ее частных производных. Предпочтительный вариант осуществления данного изобретения использует уравнения (2) и (5) для вычисления полного потенциального поля р(х), а затем использует уравнение (6) для вычисления полной потенциальной энергии и уравнение (10) для вычисления ее частных производных. Нижеследующий листинг псевдокодов подробнее описывает этот алгоритм.

АЛГОРИТМ 1: ВЫЧИСЛИТЬ Р, И

101: инициализируют полное потенциальное поле р(х)=βb(х)

102: для всех местоположений x_j=x₁, x₂, ..., x_n атомов {

103: для всех х таких, что |x-x_j|< {

104: суммируют р(х)=р(х)+(1-β)φ[|x-x_j|/d(x_j)] нарастающим итогом

105: }

106: }

107: инициализируют полную потенциальную энергию Р=0

108: для всех местоположений x_j=x₁, x₂, ..., x_n атомов {

109: суммируют

110: вычисляют

111: вычисляют

112: вычисляют

113: }

Строки 101-106 вычисляют полное потенциальное поле р(х), дискетизированное так же, как потенциальное поле b(х) изображения. При задании этого поля строки 107-113 вычисляют полную потенциальную энергию Р и ее частные производные и . В строке 109 значения полного потенциального поля и потенциального поля изображения в местоположении x_i можно аппроксимировать, как упомянуто выше, путем выбора соответствующих значений поля в ближайшем положении выборки изображения либо посредством любой желаемой схемы интерполяции. Частные производные в строках 110-112 вычисляют из полного потенциального поля с помощью простых приближений центрированных конечных разностей; однако вместо этого могут использоваться альтернативные (например, более высокого порядка) численные приближения производных. Для определенности, в этом листинге предполагается трехмерное координатное пространство. Для двумерного пространства координаты z и частные производные просто игнорируются.

В предположении, что местоположения атомов согласуются с функцией d(x) номинального расстояния, вычислительная сложность Алгоритма 1 составляет O(N), где N - число выборок в изображении. Вспомним, что дискретизировали полное потенциальное поле так же, как и изображение, и что каждый атом вносит вклад в виде пространственно ограниченной потенциальной функции (наподобие функции на фиг.3) в те выборки в полном потенциальном поле, которые лежат ближе всего к этому атому. Поэтому стоимость суммирования нарастающим итогом вкладов от всех атомов пропорциональна числу выборок N в этом поле.

Стоимость этого алгоритма сравнима со стоимостью обычной обработки изображений, и он требует структуры данных не сложнее, чем простой массив, который представляет изображение. Более того, для функций d(x) непостоянного номинального расстояния стоимость та же самая, что и для постоянного номинального расстояния d.

Альтернативный вариант осуществления

Альтернативный вариант осуществления данного изобретения не вычисляет полного потенциального поля. Вместо этого он использует уравнения (7), (8) и (9), чтобы вычислить его частные производные. Нижеследующий листинг псевдокодов описывает этот алгоритм подробнее.

АЛГОРИТМ 2: ВЫЧИСЛИТЬ Р, И

201: инициализируют полную потенциальную энергию Р=0

202: для всех местоположений x_j=x₁, x₂, ..., х_n атомов {

203: суммируют P=P+βb(x_i) нарастающим итогом

204: инициализируют

205: инициализируют

206: инициализируют

207: для всех местоположений х_j атомов таких, что {

208: суммируют нарастающим итогом

209: вычисляют Δ=(1-β)φ'[|x_i-x_j|/d(x_i)]/[d(x_i)|x_i-x_j|]

210: суммируют нарастающим итогом

211: суммируют нарастающим итогом

212: суммируют нарастающим итогом

213: }

214: }

Для каждого атома строка 203 суммирует нарастающим итогом потенциальную энергию В изображения, а строка 208 суммирует нарастающим итогом потенциальную энергию А атомов для каждого соседнего атома в полную потенциальную энергию Р. Аналогично, строки 204-206 и 210-212 суммируют нарастающим итогом вклады от частных производных полной энергии изображения и атомов в частные производные полной потенциальной энергии.

Строка 207 подразумевает использование вспомогательной структуры данных, которая позволяет быстро определять соседние атомы, ближайшие к атому, расположенному в х=х_i. Эта структура данных должна переформировываться или