Способ навигации летательных аппаратов

Способ навигации летательных аппаратов

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиолокационной техники и может быть использовано при построении различных радиолокационных (радарных) или аналогичных систем, предназначенных для определения местоположения летательных аппаратов с использованием радиоволн и управления движением летательных аппаратов.

Для обеспечения навигации летательных аппаратов (ЛА) необходимо измерение текущих координат для определения местоположения ЛА. В данном случае местоположение ЛА определяется с помощью радиоволн для применения в радиолокационных системах навигации.

В основе навигации лежат экстремальные способы [1] управления ЛА, которые предназначены для отыскания и слежения за оптимальным режимом движения ЛА. Указанные способы навигации используют свойство корреляционной функции одного или нескольких аргументов достигать максимума при нулевом значении аргументов [2], что обеспечивает повышение точности навигации. Поэтому они называются корреляционно-экстремальными способами навигации (КЭСН) [2].

КЭСН обеспечивают измерение показателей экстремального режима ЛА, переработку этой информации и выработку управляющего воздействия для коррекции координат местоположения ЛА [2]. При этом задача КЭСН состоит в отыскании положения экстремума и слежении за его возможными изменениями, которое осуществляется с помощью процесса поиска [1]. Возможны варианты КЭСН: слежение за изменением знака экстремума или слежение не только за знаком, но и его величиной [1].

Наибольшее распространение получили картосличительные КЭСН для повышения точности навигации ЛА, которые в [3] в общем виде определены как способы адаптивного управления с эталонной моделью.

Принцип работы КЭСН по геофизическим полям, реализуемый картосличительными способами навигации, основан на сравнении (сопоставлении) текущих карт местности, полученных с использованием радиоволн, с эталонными картами той же местности, априори находящимися на ЛА, в основе которых лежит определение местоположения ЛА с последующим управлением движением ЛА путем коррекции их местоположения. Эталонные карты [2, 4-5] изготавливают заранее (до начала движения ЛА над заданной поверхностью местности), а текущие снимают во время полета ЛА. По отклонениям эталонных карт местности от текущих в заданной точке траектории движения ЛА определяют отклонение фактической траектории от программной. В результате определяют поправку с целью коррекции движения ЛА.

Сравнение (сопоставление) эталонной и текущей (измеренной) карт (радиоволнового изображения местности) осуществляется посредством вычисления критериальных функционалов, достигающих глобального экстремума при полном совмещении изображений [6]. Это классический корреляционный алгоритм (ККА) [6-7], используемый КЭСН ЛА по картам полей земли [2-7]. Для обработки информации наиболее предпочтительными являются разностные алгоритмы, в частности алгоритм минимума абсолютной разности (MAP) и алгоритм минимума квадрата разности (МКР) с вычтенным средним [6-7]. Разностные алгоритмы основаны на поэлементном вычислении разностей измеренных высот текущей карты. По быстродействию разностные алгоритмы намного эффективнее, поскольку в них отсутствует операция умножения, присущая ККА [6-7].

Известен способ навигации летательных аппаратов [2], использующийся в корреляционно-экстремальных системах навигации и заключающийся в подгонке контуров местности на основе определения местоположения ЛА с использованием радиоволн, излучаемых в виде одного луча (далее: радиоволн в виде луча), позволяющий снимать информацию в текущей точке.

Реализация способа [2] заключается в следующем.

Используют информацию эталонной карты местности о навигационном поле земли, которая априори находится на ЛА (до начала движения ЛА).

Выбирают участок местности на эталонной карте (мерный участок), который определяется величиной допустимых отклонений ЛА по дальности (квадрат неопределенности).

Измеряют случайные функции двух аргументов, которыми являются пространственные координаты χ_т и γ_т («т» - параметры текущей карты местности) с использованием одного луча радиоволн.

Составляют для мерного участка текущую карту на основе измерений χ_т и γ_т.

Определяют значение функции в точке χ_э и γ_э («э» - параметры эталонной карты местности) после прохождения ЛА мерного участка.

Совмещают реализации случайных функций ϕ(χ_Т, γ_Т) текущей карты со значениями ϕ(χ_э, γ_э) эталонной карты посредством обеспечения условий

Сравнивают текущее ϕ(χ_Т, γ_Т) и эталонное ϕ(χ_э, γ_э) значения путем корреляционной обработки реализаций.

Вычисляют сигнал коррекции местоположения ЛА.

Управляют движением ЛА путем коррекции его местоположения.

Недостатками способа [2] являются:

Недостаточная оперативность алгоритма навигации, поскольку сигнал коррекции движения ЛА вырабатывается только после прохождения всего мерного участка.

Отсутствие информации о текущем местоположении ЛА в процессе движения над мерным участком.

Низкое быстродействие определения местоположения ЛА, поскольку классический корреляционный алгоритм требует достаточного большого времени для выработки сигнала коррекции местоположения ЛА, обусловленное применением операции умножения.

Известен способ навигации летательных аппаратов [8], выбранный за прототип.

Реализация способа [8] заключается в следующем.

Используют информацию эталонной карты местности о навигационном поле земли, которая априори находится на ЛА (до начала движении ЛА).

Выбирают участок местности (мерный участок), который определяется величиной допустимых отклонений ЛА по дальности (квадрат неопределенности).

Измеряют с использованием одного луча радиоволн случайные функции, которыми являются значения высот («т» - параметры текущей карты) от ЛА до рельефа мерного участка в точках i (i=1,2,3,...N) траектории движения ЛА (трассы ).

Вычисляют после прохождения ЛА мерного участка отклонения высот измеренные с помощью радиоволн, от высот , измеренных бародатчиком (абсолютная высота), в точках i траектории движения ЛА

Составляют для мерного участка текущую карту на основе вычисленных высот рельефа после прохождения мерного участка, то есть получают карту высот рельефа мерного участка (плановые координаты мерного участка), для составления которой используют данные о скорости ЛА и углах эволюции (тангаж, крен и курс), поступающих с периодом T_С.

Определяют на основе эталонной карты местности трассы («э» - параметры эталонной карты местности), направленные вдоль мерного участка с шагом j (j=1,2,3,...N) поперек мерного участка, соответствующим шагу эталонной карты (плановые координаты эталонной карты).

Совмещают текущую и эталонную карты исследуемой местности.

Сравнивают текущее и эталонное значения путем корреляционно-экстремальной обработки реализаций с использованием алгоритма MAP.

Вычисляют сигнал коррекции местоположения ЛА на основе анализа различий (взаимных смещений) эталонной и текущей карт местности мерного участка.

Управляют движением ЛА путем коррекции его местоположения.

В данном КЭСН траектория движения ЛА разделена на автономный участок (наблюдение) и участок коррекции без их возможного сочетания.

Недостатками способа [8] являются:

Выработка сигнала коррекции только после пролета всего мерного участка.

Необходимость измерения абсолютной высоты ЛА над нулевым уровнем Н₀ эталонной карты для ККА.

В случае использования алгоритмов с вычтенным средним (MAP и МКР) требования знания абсолютной высоты не предъявляются, но необходимы дополнительные вычисления для определения средних уровней высот измеренной карты и эталонной карты. Необходимость таких вычислений не позволяет реализовать скользящую обработку данных.

Низкая точность составления текущей карты с использованием одного луча, поскольку для измерения высоты до исследуемой местности ширина луча радиоволн должна быть достаточно широкой. При этом снижается точность определения дальности до отдельных точек поверхности и, соответственно, снижается точность составления текущей карты.

Отсутствие информации о текущем местоположении ЛА в процессе движения над мерным участком (автономный участок), поскольку обработка измеренной информации осуществляется только после пролета всего мерного участка на участке коррекции.

Низкое быстродействие определения местоположения ЛА, поскольку классический корреляционный алгоритм требует достаточного большого времени для выработки сигнала коррекции местоположения ЛА, обусловленное применением операции умножения.

Техническим результатом предлагаемого изобретения является повышение быстродействия способа навигации летательных аппаратов за счет оперативной обработки получаемой информации.

Технический результат достигается тем, что в способе навигации летательных аппаратов, заключающемся в использовании эталонной карты местности как априорной информации о навигационном поле, выборе участка местности (мерный участок), находящегося в пределах эталонной карты, составлении текущей карты путем вычисления плановых координат мерного участка на основе измерений наклонных дальностей с помощью радиоволн, сравнении значений плановых координат текущей и эталонной карт, вычислении сигнала коррекции траектории движения и управлении движением летательных аппаратов путем коррекции их местоположения, используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, количество которых составляет не менее трех и определяется допустимым временем измерения местоположения летательных аппаратов при движении над мерным участком, используемые радиоволны излучают в виде лучей, которые воздействуют последовательно на исследуемую поверхность, причем первоначально излучают луч, расположенный в плоскости, ортогональной плоскости горизонта исследуемой поверхности (первый луч), следующими излучают лучи, направление распространения которых не совпадает с направлением распространения первого луча, причем направления распространения одной части лучей находятся слева (по направлению движения летательного аппарата) от первого луча, а другой части - справа (по направлению движения летательного аппарата) от первого луча (количество лучей справа и слева от первого луча одинаковое), используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, которые при воздействии на исследуемую поверхность расположены в плоскости, ортогональной плоскости горизонта исследуемой поверхности, используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, которые при воздействии на исследуемую поверхность расположены в плоскости, находящейся под углом к плоскости горизонта исследуемой поверхности, используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, которые при воздействии на исследуемую поверхность расположены в разных плоскостях между собой, используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, направления распространения которых составляют между собой и первым лучом одинаковые углы, используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, направления распространения которых составляют между собой и первым лучом различные углы, при вычислении сигнала коррекции местоположения летательных аппаратов для измерения параметров мерного участка определяют разности измерений второго и первого лучей, третьего и первого лучей и так далее вплоть до определения разности измерений предпоследнего и первого лучей, последнего и первого лучей в текущем измерении, а также вычисляют разность измерений первого луча в текущем измерении и в предыдущем, аналогичные вычисления производят по эталонной карте для каждого возможного положения летательного аппарата внутри квадрата неопределенности и вычисляют показатель близости данных, позволяющий оперативно управлять движением летательных аппаратов.

Технический результат достигается тем, что при реализации способа навигации летательных аппаратов для составления текущей карты используют многолучевой режим измерения при помощи радиоволн, а для вычисления сигнала коррекции местоположения летательных аппаратов и управления их движением определяют разности результатов многолучевых измерений. При этом для повышения быстродействия способа навигации используют дифференциально-разностный алгоритм обработки поступающей информации. В результате способ навигации ЛА позволяет использовать информацию о текущих точках траектории ЛА в процессе движения над мерным участком для коррекции местоположения ЛА до момента прохождения всего мерного участка, что обеспечивает повышение быстродействия способа навигации летательных аппаратов. В результате способ навигации позволяет управлять движением ЛА при прохождении мерного участка, а не после прохождения всего мерного участка эталонной карты, как это сделано в аналогах и прототипе.

Задачей КЭСН является уточнение местоположения ЛА, определенного иными средствами навигации. Уточнение координат (определение поправок к координатам) производится в пределах области, определяемой погрешностью этих средств навигации. Пусть упомянутая область имеет форму квадрата, сторона которого равна удвоенной погрешности иных средств навигации, и называется квадрат неопределенности.

Способ навигации ЛА поясняют следующие чертежи:

- на фигуре 1 представлено взаимное расположение систем координат при движении ЛА;

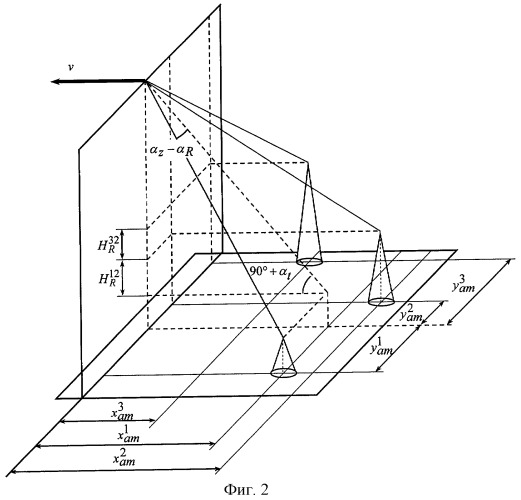
- на фигуре 2 показано измерение наклонной дальности по отдельным лучам радиоволн;

- на фигуре 3 представлен показатель близости данных.

Способ навигации ЛА осуществляется следующим образом.

До начала движения ЛА используют информацию эталонной карты местности о навигационном поле земли, которая априори находится на ЛА.

Выбирают необходимый участок местности эталонной карты, который представляет собой мерный участок и определяется величиной допустимых отклонений ЛА по дальности (квадрат неопределенности).

Составляют текущую карту путем измерения параметров мерного участка с помощью радиоволн. При этом используемые радиоволны при излучении представляют собой лучи, которые воздействуют на исследуемую поверхность последовательно, число которых составляет не менее трех и определяется допустимым временем измерения местоположения ЛА при движении над мерным участком. Лучи радиоволн излучают следующим образом. Первоначально излучают луч, направление распространения которого расположено в плоскости, ортогональной плоскости горизонта исследуемой поверхности (первый луч). Потом излучают лучи, направление распространения которых не совпадает с направлением распространения первого луча, причем направления распространения одной части лучей находятся слева (по направлению движения ЛА) от первого луча, а другой части - справа (по направлению движения ЛА) от первого луча. Причем количество лучей справа и слева от центрального луча одинаковое. При воздействии радиоволн на исследуемую поверхность лучи в зависимости от поставленной задачи располагают либо в одной плоскости, либо в разных плоскостях. Радиоволны излучают (воздействуют) на исследуемую поверхность в виде лучей, расположенных под углом или перпендикулярно к плоскости горизонта исследуемой поверхности. Вычисляют местоположение ЛА в плановых координатах мерного участка на основе измерений наклонных дальностей с помощью лучей радиоволн.

Текущую карту получают последовательно по мере прохождения отдельных частей мерного участка (информация о мерном участке поступает до истечения его полного прохождения - в темпе поступления измеренной информации).

Вычисляют значения плановых координат текущей карты по мере прохождения мерного участка путем вычисления разностей результатов многолучевых измерений. Для этого определяют разности измерений второго и первого лучей, третьего и первого лучей и так далее вплоть до определения разности измерений предпоследнего и первого лучей, последнего и первого лучей в текущем измерении, а также вычисляют разность измерений первого луча в текущем измерении и в предыдущем. Так, для трех лучей радиоволн определяют разности измерений левого и первого (центрального) лучей, правого (последнего) и первого лучей текущего измерения, а также вычисляют разность измерений первого луча в текущем измерении и в предыдущем.

Проводят вычисления, аналогичные описанным выше, по эталонной карте для каждого возможного положения летательного аппарата внутри квадрата неопределенности (для каждой гипотезы).

Совмещают и сравнивают полученные значения плановых координат текущей и эталонных карт.

Вычисляют показатель близости данных в результате сравнения текущей и эталонных карт.

Определяют траекторию движения ЛА (местоположение) на эталонной карте.

Управляют движением ЛА путем коррекции их местоположения (траектории движения) в заданных точках траектории по мере прохождения мерного участка. Управление движением ЛА осуществляется оперативно, поскольку по мере прохождения мерного участка оперативно осуществляется коррекция местоположения ЛА.

Способ навигации реализуется следующим образом.

Реализацию способа навигации ЛА рассмотрим на примере составления текущей карты с помощью трех лучей радиоволн (с равными углами между левым и правым лучами относительно центрального (первого) луча), расположенных в одной плоскости, которая находится под углом к плоскости горизонта исследуемой поверхности.

В течение времени Т_х движения над мерным участком определяют текущую карту местности, для составления которой используют данные об измеренных значениях наклонной дальности с помощью лучей радиоволн, а также значения скорости и углах эволюции ЛА (тангаж, крен и курс), поступающих с периодом T_C.

Для удобства представления информации будем применять три системы координат (фиг.1): большой прямоугольник представляет собой эталонную карту рельефа местности; квадрат является квадратом неопределенности; возможные положения ЛА внутри квадрата неопределенности в момент начала измерений (гипотезы) обозначены точками, а точки траектории ЛА, в которых производят измерения, обозначены ромбами.

Определим местную систему координат как левую прямоугольную декартову систему координат O_rx_ry_rz_r с началом O_r. Полагаем, что оси O_rx_r и O_ry_r лежат в плоскости местного горизонта, то есть x_r и y_r являются плановыми координатами ЛА. Относительно плоскости O_rx_rУ_r определяют высоты рельефа местности и ЛА. Таким образом, указанные высоты являются соответствующими значениями координаты z_r.

Начало координат O_r выбрано так, что ось O_ry_r направлена в расчетную точку появления ЛА над участком местности, соответствующим эталонной карте. Ось О_rУ_r считается коллинеарной по отношению к горизонтальной составляющей расчетного вектора скорости ЛА (фиг.1). Плановая система координат неподвижна и связана с эталонной картой.

Для того чтобы привязать плановые координаты к эталонной карте (которая задана в виде массива), используют дискретную систему координат. Ее оси N_x и N_y сонаправлены с осями местной системы О_rx_ry_r (фиг.1). Нулевым индексам в дискретной системе координат соответствует левый нижний угол эталонной карты. Предполагаемое значение дискретных координат ЛА в момент начала сбора данных обозначим как (n_xr0, n_yr0).

Следовательно, координаты точки О_r (начало местной системы координат) в дискретной системе будут равны (n_xr0, n_yr0). Связь между координатами дискретной и местной систем координат определяется выражениями

где Δ₀ - размер ячейки сетки эталонной карты.

При определении координат точек измерений (точек пересечения подстилающей поверхности и лучей радиоволн) используют систему координат, связанную с текущим положением ЛА. Начало координат этой системы - точку O_α - поместим в текущую точку проекции траектории ЛА на плоскость плановых координат. Ось О_αx_α по направлению совпадает с текущим направлением вектора скорости ЛА. Связь между координатами системы, связанной с ЛА, и местной системы координат определяется выражениями

где x_rc и У_rc - координаты проекции текущего положения ЛА на плоскость плановых координат; α_х - курс ЛА в текущей точке измерений (угол между вектором скорости ЛА и осью О_rx_r).

Исходными данными для вычислений в КЭСН являются:

- эталонная карта, представляющая собой двумерный массив данных о рельефе местности, элементы которого представляют собой высоты рельефа в узлах координатной сетки эталонной карты на плоскости О_rx_ry_r (узлы совпадают с узлами дискретной системы координат);

- данные, обусловленные особенностями решаемой задачи (общее время измерений Т_x и интервал времени между измерениями Т_c);

- данные, определяемые конструкцией ЛА (угол между лучами αR радиоволн);

- данные измерений, отличных от полученных с помощью лучей радиоволн, поступающие с каждым результатом измерений (с интервалом Т_с): значения угла α_z крена, угла α_x курса, угла α_t тангажа, скорости ν ЛА;

- текущая карта, представляющая собой набор значений наклонных дальностей по всем трем лучам, полученных в каждом измерении.

Определим показатель близости данных - функционал, положение глобального экстремума которого определяет точку совмещения изображений (текущей и эталонных карт) при следующих условиях. Пусть текущая карта местности представлена матрицей Н_R(n_x, n_у) размером N_xR×N_yR, а эталонная карта - матрицей Н₀(n_x,n_у) размером N_x0×N_y0. Дискретные величины n_sx и n_sy соответствуют горизонтальному и вертикальному смещению текущей карты относительно эталонной и отсчитываются от левого нижнего угла эталонной карты, для которого n_sx=n_sy=0. Тогда показатель близости данных запишется в виде

где р=0, 1, 2,....

Для р=1 получим алгоритм минимума абсолютной разности (MAP), который и будет использоваться для анализа.

Для того чтобы избежать появления ложных экстремумов, вызванных различиями в средних высотах эталонной и текущей карт, выполняют центрирование данных. Поэтому для разностных алгоритмов с вычтенным средним показатель близости имеет вид

где M_HR - среднее значение высоты по данным текущей карты, M_НО (n_sx, n_sy) - среднее значение высоты участка эталонной карты, получаемое в результате совмещения карт.

В предлагаемом способе используют многолучевой режим измерения при помощи радиоволн, а при вычислении сигнала коррекции определяют разности результатов многолучевых измерений. Таким образом, используют дифференциально-разностный алгоритм обработки многолучевых измерений (ДРАОМИ), который рассмотрим на примере трехлучевого КЭСН. Лучи радиоволн назовем: центральный или первый (по направлению движения ЛА), левый и правый относительно центрального луча, которые излучают последовательно в следующем порядке: центральный луч, левый луч, правый луч.

Используемый алгоритм состоит в определении разности измерений левого и центрального лучей, правого и центрального лучей текущего измерения, а также вычисляют разности измерений центрального луча в текущем измерении и в предыдущем.

По эталонной карте для каждой гипотезы определяют положение координат в каждой точке, для которой рассчитывается высота рельефа местности на мерном участке.

Выражение для показателя близости данных согласно ДРАОМИ имеет вид

где для обозначения разностей измерений лучей применена двойная индексация: верхний индекс 12 означает вычитание результата измерения по центральному лучу из результатов измерения по левому, а верхний индекс 32 - вычитание результата по центральному лучу из результата по правому.

Такой подход позволяет производить вычисления без знания абсолютного значения высоты движений ЛА. При этом не требуется выполнять дополнительные расчеты для определения средних значений высот рельефа по текущей и эталонной картам.

Обработку данных каждого измерения производят следующим образом.

По полученным данным о наклонных дальностях, а также об углах эволюции вычисляют координаты точек измерений в системе координат, связанной с ЛА, а также измеренные значения высоты в этих точках.

Вычисляют местные координаты проекции текущей точки траектории ЛА на плоскость плановых координат.

Для каждой гипотезы, то есть для всех возможных положений ЛА внутри квадрата неопределенности вычисляется одно слагаемое показателя близости.

По завершении всех измерений проводят поиск экстремума показателя близости.

Выдают поправки к координатам местоположения ЛА.

Рассмотрим данный алгоритм подробно.

По измеренным значениям наклонных дальностей до элементов подстилающей поверхности (j∈[1,3] - номер луча радиоволн) определяют координаты точек измерений в системе координат, связанной с ют координаты точек измерений в системе координат, связанной с ЛА, а также измеряемые значения высоты рельефа .

Согласно фиг.2 для левого луча получим

Аналогичным образом производят вычисления по данным двух других лучей радиоволн.

По полученным данным о скорости и углах эволюции определяют координаты проекции точки траектории ЛА на плоскость плановых координат.

Для первого измерения эти координаты считаются нулевыми (то есть положение ЛА во время первого измерения совпадает с началом координат системы О_rx_ry_r)

Местные координаты ЛА во время выполнения следующих измерений вычисляют по рекуррентным соотношениям.

где i=1, 2,... - номер текущего измерения.

Зная координаты точек измерений в системе координат, связанной с ЛА (О_αx_αy_α), и местные координаты начала О_α, определяют координаты точек измерений в местной системе координат

Перебор гипотез заключается в следующем. Для каждого из возможных положений ЛА в пределах квадрата неопределенности вычисляют координаты (в дискретной системе координат) точек измерений, определенные ранее в местной системе координат. Для этого точку О_r помещают поочередно в узлы координатной сетки внутри квадрата неопределенности и выполняют вычисление показателя близости данных. Координаты точек измерений в дискретной системе координат определяют как

где n_hx и n_hy - смещения точки О_r для различных гипотез, определенные в количестве узлов сетки эталонной карты.

Приведенное выше общее выражение для показателя близости данных ДРАОМИ в применении к решаемой задаче имеет вид

Здесь n_hx и n_hy - смещения точки О_r для различных гипотез; К - количество измерений; - разность измеренных в k-м измерении значений высоты по левому и центральному лучам; - разность измеренных в k-м измерении значений высоты по правому и центральному лучам; - разность значений высоты, измеренных в k-м и (k-1)-м измерениях; - разность определенных для некоторой гипотезы (для определенного значения n_hx и n_hy) значений высоты по данным эталонной 32 k карты на k-м измерении по левому и центральному лучам; - разность определенных для некоторой гипотезы значений высоты по данным эталонной карты на k-м измерении по правому и центральному лучам; - разность определенных для некоторой гипотезы значений высоты по данным эталонной карты на k-м и (k-1)-м измерениях по центральному лучу.

Выражение (13) позволяет сделать вывод о возможности скользящей обработки данных. При поступлении результатов первого измерения для каждой гипотезы вычисляют выражение под знаком суммы и сохраняют в массиве - показателе близости. Во время всех остальных измерений вновь получаемые значения выражения под знаком суммы складывают с соответствующими значениями в массиве D(n_hx,n_ny) и результат вновь записывают в массив.

По завершении всех измерений производят поиск глобального экстремума (в случае ДРАОМИ - минимума) показателя близости данных D(n_hx, n_hy), который представляет собой двумерную функцию от предполагаемого значения координат ЛА в момент начала измерений внутри квадрата неопределенности. Показатель близости может иметь вид, например, показанный на фиг.3.

Для проверки используемого в КЭСН алгоритма обработки ДРАОМИ были проведены его экспериментальные исследования. Для этого моделировались процессы, происходящие в системе навигации. Полученные результаты сравнивались с известными алгоритмами ККА, MAP и МКР. Отметим, что для данных алгоритмов требуется наличие информации обо всех элементах текущей карты для вычисления среднего значения высоты по данным текущей карты и среднего значения высоты участка эталонной карты, получающегося в результате совмещения карт, что делает невозможным скользящую (одновременную) обработку данных совместно с их накоплением. Кроме этого, существует также необходимость:

- в знании абсолютной высоты ЛА над нулевым уровнем эталонной карты для получения надежных результатов при использовании алгоритма минимума абсолютной разности;

- в дополнительных вычислениях для определения средних уровней высот измеренной карты и эталонной карты при использования алгоритмов с вычтенным средним, что не позволяет реализовать скользящую обработку данных.

При сравнении время вычислений при использовании классического корреляционного алгоритма выбиралось за исходное при сравнении и считалось равным 100%.

Результаты исследований приведены в таблице.Таблица
Наименование алгоритма	Время вычислений, в процентах от ККА
ККА	100,0
МКР	72,5
MAP	67,1
ДРАОМИ	30,0

Таким образом, экспериментальные исследования путем моделирования алгоритмов обработки навигационной информации в КЭСН используемый алгоритм (ДРАОМИ) позволяет уменьшить время необходимых вычислений:

- на 42,5% по сравнению с алгоритмом МКР;

- на 37,1% по сравнению с алгоритмом MAP;

- более чем в три раза по сравнению с наиболее известным алгоритмом ККА.

Важно отметить, что рассмотренный способ навигации ЛА с алгоритмом ДРАОМИ сохраняет свои положительные свойства при различном количестве лучей радиоволн и обеспечивает работоспособность и для трех, и для большего количества (например, для пяти и более) лучей радиоволн. Число используемых лучей радиоволн определяется допустимым временем измерения местоположения ЛА при движении над мерным участком исследуемой поверхности (увеличение количества лучей ведет к существенному увеличению поступаемой информации за один такт измерения, что уменьшает время измерений местоположения ЛА).

Применение многолучевого (количество лучей радиоволн составляет не менее трех) режима составления текущей карты местности позволяет осуществить наибольший охват исследуемой местности при минимальной ширине луча радиоволн и наибольшем энергетическом потенциале, что повышает точность определения дальности до отдельных точек поверхности и, соответственно, повышает точность составления текущей карты.

Необходимо отметить, что в способе навигации ЛА по сравнению с аналогом и прототипом исключены: операция умножения, характерная для классического корреляционного алгоритма для выработки сигнала коррекции местоположения ЛА; информация обо всех элементах текущей карты для вычисления среднего значения высоты по данным текущей карты и среднего значения высоты участка эталонной карты; информация об абсолютной высоте ЛА над нулевым уровнем эталонной карты; дополнительные вычисления для определения средних уровней высот измеренной карты и эталонной карты. В конечном итоге появляется возможность использования скользящего режима обработки данных - использование информации о текущих точках траектории ЛА в процессе движения над мерным участком, что обеспечивает повышение быстродействия способа навигации летательных аппаратов.

Таким образом, способ навигации летательных аппаратов обладает рядом существенных преимуществ перед прототипом и аналогом.

ЛИТЕРАТУРА

1. Цыпкин Я.З., Попков Ю.С. Теория нелинейных импульсных систем. - М.: Наука, 1973. - 414 С. (С.303-304).

2. Белоглазов И.Н., Тарасенко В.П. Корреляционно-экстремальные системы. - М.: Сов. радио, 1974. - 392 С. (С.3,27-32).

3. Александров А.Г. Оптимальные и адаптивные системы. - М.: Высш. шк., 1989. - 264 С. (С.142, 163, 181, 187).

4. Бочкарев A.M. Корреляционно-экстремальные системы навигации // Зарубежная радиоэлектроника. - 1981. - N 9. - С.28-53.

5. Андреев Г.А., Потапов А.А. Активные системы ориентации по географическим полям // Зарубежная радиоэлектроника. - 1988. - N 9. - С.62-85, 39. (С.80).

6. Андреев Г.А., Потапов А.А. Алгоритмы обработки навигационной пространственно-временной информации. Ч.1 // Зарубежная радиоэлектроника. - 1989. - N 3. - С.3-18.

7. Андреев Г.А., Потапов А.А. Алгоритмы обработки навигационной пространственно-временной информации. Ч.2 // Зарубежная радиоэлектроника. - 1989. - N 4. - С.3-21.

8. Ржевкин В.А. Автономная навигация по картам местности // Зарубежная радиоэлектроника. - 1981. - N 10. - С.3-28. (прототип, с.7-8).

1. Способ навигации летательных аппаратов, заключающийся в использовании эталонной карты местности как априорной информации о навигационном поле, выборе участка местности (мерный участок), находящегося в пределах эталонной карты, составлении текущей карты путем вычисления плановых координат мерного участка на основе измерений наклонных дальностей с помощью радиоволн, сравнении значений плановых координат текущей и эталонной карт, вычислении сигнала коррекции траектории движения и управлении движением летательных аппаратов путем коррекции их местоположения, отличающийся тем, что при составлении текущей карты используют многолучевой режим измерения при помощи радиоволн, при вычислении сигнала коррекции местоположения летательных аппаратов определяют разности результатов многолучевых измерений.

2. Способ по п.1, отличающийся тем, что используемые радиоволны при измерении параметров мерного участка излучают в виде лучей, количество которых составляет не ме