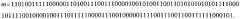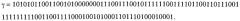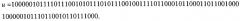Способ формирования ключа шифрования

Способ формирования ключа шифрования

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области информационной безопасности телекоммуникационных систем и, в частности, может быть использовано в криптографических системах с открытым распределением ключей шифрования.

Известен способ формирования ключа шифрования у абонентов конфиденциального сеанса связи, включающий преобразование случайного многоразрядного двоичного числа, называемого временной отметкой и определяемого по моменту времени, например по моменту времени начала сеанса связи, по заранее оговоренному криптографическому алгоритму под управлением секретного ключа, которым абоненты обмениваются предварительно по защищенному каналу связи [М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001, с.197-198]. Недостатком этого способа формирования ключа шифрования является необходимость передачи секретного ключа по защищенному каналу связи, который является дорогостоящим элементом систем секретной связи.

Также известен способ формирования ключей шифрования путем многократного последовательного модифицирования секретного ключа в соответствии с алгоритмом одностороннего преобразования [М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001, с.205]. Недостатком известного способа формирования ключа шифрования является то, что при компрометации текущего ключа компрометируются все последующие ключи шифрования данных.

Наиболее близким по своей технической сущности к заявленному является известный способ формирования ключа шифрования с использованием открытых каналов связи, описанный в книге [Молдовян Н.А., Молдовян А.А., Еремеев М.А. Криптография: от примитивов к синтезу алгоритмов. - СПб, БХВ-Петербург, 2004, 436 с., с.408 и с.412-413]. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий:

1. У получателя информации формируют открытый ключ в виде двух многоразрядных двоичных чисел (МДЧ) первого р и второго α (здесь и далее по тексту описания под многоразрядным двоичным числом следует понимать электромагнитный сигнал в двоичной цифровой форме, в котором общее число битов и порядок их следования отражает некоторое двоичное число), для чего

генерируют первый m и второй n вспомогательные простые множители в виде МДЧ, а первое МДЧ р открытого ключа вычисляют как произведение р=mn;

вычисляют функцию Эйлера ϕ(р) от первого р МДЧ открытого ключа по формуле ϕ(р)=(m-1)(n-1);

генерируют второе МДЧ α открытого ключа, являющееся взаимно простым со значением функции Эйлера ϕ(р) (пара из первого р и второго α МДЧ образуют открытый ключ);

вычисляют секретное МДЧ γ=α^-1 mod ϕ(p), при котором выполняется условие γα mod ϕ(р)=1.

2. Передают, например, по телекоммуникационным сетям открытый ключ, т.е. первое р и второе α МДЧ открытого ключа, отправителю информации.

3. Формируют у отправителя информации образ ключа шифрования в виде МДЧ R, для чего генерируют случайное МДЧ Т, а образ ключа шифрования вычисляют по формуле R=T^α mod р.

4. Передают получателю информации образ ключа R.

5. У получателя информации вычисляют ключ шифрования T по формуле T=R^γ mod р.

При таком способе оказывается возможным открытое распределение ключей, т.е. без использования защищенных каналов связи, что снижает затраты на обеспечение информационной безопасности.

Однако известный способ имеет недостаток - относительно большое время, необходимое для формирования ключа шифрования, что связано с необходимостью выполнения большого объема вычислений у получателя информации, обусловленного большой разрядностью МДЧ γ, примерно равной разрядности первого р МДЧ открытого ключа, которую для достижения требуемой криптостойкости выбирают в пределах 1024-2048 бит.

Целью изобретения является разработка способа формирования ключа шифрования, обеспечивающего уменьшение времени, необходимого для формирования ключа шифрования за счет снижения объема вычислений по формированию ключа шифрования при сохранении требуемой его криптостойкости.

Кроме того, заявленное техническое решение расширяет арсенал средств данного назначения.

Поставленная цель достигается тем, что в известном способе формирования ключа шифрования, заключающемся в том, что у получателя информации формируют открытый ключ в виде первого р и второго α многоразрядных двоичных чисел, передают его отправителю информации, у которого формируют образ ключа шифрования в виде многоразрядного двоичного числа R и передают его получателю информации, где вычисляют ключ шифрования в виде многоразрядного двоичного числа К, для формирования открытого ключа у получателя информации вычисляют первое МДЧ р открытого ключа, функция Эйлера ϕ(p) от которого содержит, по крайней мере, один множитель γ в виде простого ξ-разрядного двоичного числа. Разрядность ξ простого множителя γ выбирают в интервале 64≤ξ≤256 бит. Затем генерируют произвольное МДЧ β и вычисляют второе МДЧ α открытого ключа по формуле α=β^ϕ(р)/γ mod р, для которого выполняется условие α^ϕ(р)/γ mod р=1.

Новым также является то, что для формирования образа R ключа шифрования К у отправителя информации генерируют случайное σ-разрядное двоичное число W, причем разрядность σ выбирают из условия σ≤ξ.

Образ ключа шифрования рассчитывают по формуле R=(α^W mod р)^t mod р, где t - показатель, предварительно заданный получателю и отправителю информации и значение которого выбирают из условия 2≤t≤256.

Новым также является то, что для вычисления ключа шифрования К у получателя информации рассчитывают дополнительное МДЧ Z=t^-1 mod γ, после чего ключ шифрования вычисляют по формуле К=R^Z mod р.

Новым также является то, что для вычисления первого МДЧ р открытого ключа генерируют первый вспомогательный простой множитель в виде МДЧ m. Генерируют простой множитель γ в виде ξ-разрядного двоичного числа и дополнительное случайное четное МДЧ u. Затем вычисляют второй вспомогательный простой множитель n в виде случайного МДЧ n=γu+1. После чего первое МДЧ р открытого ключа вычисляют как произведение первого m и второго n вспомогательных простых множителей, т.е. p=mn.

Благодаря новой совокупности существенных признаков появляется возможность использования операции модульного возведения в степень меньшей разрядности (т.е. меньшего размера), за счет чего достигается снижение объема вычислений по формированию ключа шифрования. Последнее обеспечивает сокращение времени, затрачиваемого на формирование ключа шифрования без снижения криптостойкости.

Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют в известных источниках информации, что указывает на соответствие заявленного изобретения условию патентоспособности "новизна".

Результаты поиска известных решений в данной и смежных областях с целью выявления признаков, совпадающих с отличительными от ближайшего аналога признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники, что указывает на соответствие заявленного изобретения условию "изобретательский уровень".

Возможность реализации заявленного способа объясняется следующим образом. Известно, что разложение первого МДЧ р открытого ключа на два простых множителя n и m, представляющих собой двоичные числа достаточно большой разрядности, является вычислительно сложной задачей и при разрядности МДЧ р, равной 1024 бит и более, она практически неразрешима [Шнайер Б. Прикладная криптография - М., Издательство ТРИУМФ, 2002, с.521-522]. Высокая сложность разложения первого МДЧ р открытого ключа на простые множители лежит в основе стойкости заявляемого способа (а также и ближайшего аналога). Без разложения первого МДЧ р открытого ключа практически невозможно определить простой ξ-разрядный множитель γ, являющийся секретным ключом. Без знания МДЧ γ невозможно выполнить операцию извлечения корня второй и более высоких степеней (t≥2) из образа R ключа шифрования. Поэтому никто, кроме владельца секретного ключа, т.е. получателя информации, не сможет вычислить ключ шифрования по образу R, передаваемому от отправителя информации по открытым каналам связи. Возможность вычисления ключа шифрования получателем информации, знающим секретное МДЧ γ, обеспечивается тем, что отправитель информации формирует образ ключа по формуле R=[α^W mod p]^t mod p, где второе МДЧ α открытого ключа является числом, относящимся к показателю γ по модулю р. В силу последнего получатель информации легко вычисляет ключ шифрования К по следующей формуле: К=R^Z mod p. Так как вычисленный по такой формуле ключ шифрования равен К=α^W mod p, то действительно имеем:

Поскольку отправитель информации вычислил число К=α^W mod p, то он его знает и может использовать для шифрования информации, передаваемой получателю.

Ниже приведен пример реализации заявленного способа.

Пример реализации заявляемого способа.

1. Задают отправителю и получателю информации показатель t, например t=7. Значение t выбирают не более 256, так как при больших значениях t снижение объема вычислений будет незначительным.

2. Формируют открытый ключ у получателя информации, для чего:

2.1. Вычисляют первое МДЧ p открытого ключа, функция Эйлера ϕ(p) которого содержит, по крайней мере, один простой ξ-разрядный множитель γ, для чего:

2.1.1. Генерируют (например, с помощью генератора случайных чисел) первый вспомогательный простой множитель m в виде МДЧ, например 133-разрядный:

Разрядность множителя m выбирают из соображений получения требуемой криптостойкости и на практике ее значение берут в интервале 400-1600 бит.

2.1.2. Вычисляют второй вспомогательный простой множитель n в виде МДЧ, для чего:

2.1.2.1. Генерируют простой множитель γ в виде ξ-разрядного МДЧ (например, ξ=109).

Значение ξ выбирают из соображений получения большого числа вариантов возможного значения простого множителя γ и на практике ее значение берут обычно в пределах 64-256 бит.

2.1.2.2. Генерируют дополнительное случайное четное МДЧ u (например, 91-разрядное).

Разрядность МДЧ u выбирают из соображений получения требуемой разрядности второго вспомогательного множителя n и на практике ее значение берут в интервале 140-1350 бит.

2.1.2.3. Вычисляют второй вспомогательный простой множитель n в виде МДЧ по формуле n=γu+1.

2.1.3. Вычисляют первое МДЧ открытого ключа р как произведение первого m и второго n вспомогательных простых множителей, т.е. p=mn.

Функция Эйлера ϕ(р) от числа р равна

ϕ(р)=(m-1)(n-1)=(m-1)(γu+1-1)=(m-1)γu.

Из этого соотношения видно, что простой множитель γ действительно содержится в разложении функции, что позволяет выполнить сформулированные требования к открытому ключу.

2.2. Вычисляют второе МДЧ α открытого ключа, для чего:

2.2.1. Генерируют произвольное случайное МДЧ β (например, 270-разрядное)

Разрядность β может выбираться произвольно от 2 до 2048 бит.

2.2.2. Вычисляют функцию Эйлера ϕ(р) от первого МДЧ р открытого ключа по формуле ϕ(р)=(m-1)(n-1):

2.2.3. Вычисляют второе МДЧ α открытого ключа по формуле α=β^ϕ(p)/γ mod n:

3. Передают открытый ключ от получателя к отправителю информации, т.е. передают первое p и второе α МДЧ.

4. Формируют у отправителя информации образ ключа R в виде МДЧ, для чего

4.1. Генерируют случайное σ-разрядное МДЧ W (например, σ=107):

Значение σ должно быть меньше значения ξ, чтобы исключить выполнение дополнительной операции взятия остатка от деления МДЧ W на множитель γ.

4.2. Вычисляют у отправителя информации образ R ключа шифрования по формуле R=[α^W mod p]^t mod p. С учетом предварительно заданного значения показателя t=7 имеем:

5. Передают образ R ключа шифрования от отправителя к получателю информации.

6. Вычисляют у получателя информации ключ шифрования К, для чего

6.1. Рассчитывают дополнительное МДЧ Z по формуле Z=t^γ-2 mod γ:

6.2. Вычисляют ключ шифрования К в виде МДЧ по формуле K=R^Z mod p:

В результате выполненных шагов ключ шифрования сформирован у получателя информации без использования защищенных каналов связи, причем нарушитель, перехватывающий образ ключа шифрования, принципиально не может вычислить сам ключ шифрования, не владея ξ-разрядным секретным множителем γ.

Таким образом, показано, что заявляемый способ может быть положен в основу стойких систем открытого распределения секретных ключей. Так как при вычислении ключа шифрования К по его образу R используется возведение в степень, равную двоичному числу с относительно малой разрядностью, то обеспечивается существенное снижение времени, необходимого для формирования ключа шифрования.

Действительно, при заданной разрядности первого МДЧ р открытого ключа, например 1024-разрядного, для прототипа формирование ключа связано с необходимостью возведения значения образа ключа R в степень примерно такой же разрядности (т.е. разрядности 1024), а в заявленном способе возведение осуществляется в степень Z, разрядность которой равна разрядности ξ секретного множителя γ, которая выбирается в пределах 64≤ξ≤256. Для этого примера объем вычислений снижается в 4-16 раз, т.е. достигается сформулированный технический результат при использовании заявленного способа.

1. Способ формирования ключа шифрования, заключающийся в том, что у получателя информации формируют открытый ключ в виде первого р и второго α многоразрядных двоичных чисел, передают его отправителю информации, у которого формируют образ ключа шифрования в виде многоразрядного двоичного числа R и передают его получателю информации, где вычисляют ключ шифрования в виде многоразрядного двоичного числа К, отличающийся тем, что для формирования открытого ключа у получателя информации вычисляют первое многоразрядное двоичное число р открытого ключа, функция Эйлера ϕ(p) от которого содержит, по крайней мере, один простой множитель γ в виде ξ-разрядного двоичного числа, после чего генерируют произвольное многоразрядное двоичное число β и вычисляют второе многоразрядное двоичное число α открытого ключа по формуле α=β^ϕ(p)/γ mod р, для которого выполняется условие α^ϕ(p)/γ mod р=1, а для формирования образа R ключа шифрования у отправителя информации генерируют случайное σ-разрядное двоичное число W, а образ R ключа шифрования рассчитывают по формуле R=[α^W mod p]^t mod р, где t - показатель, предварительно заданный получателю и отправителю информации, причем для вычисления ключа шифрования К у получателя информации рассчитывают дополнительное многоразрядное двоичное число Z=t^γ-2 mod γ, после чего ключ шифрования вычисляют по формуле К=R^Z mod p.

2. Способ по п.1, отличающийся тем, что простой множитель у выбирают с разрядностью ξ в интервале 64≤ξ≤256 бит.

3. Способ по п.1, отличающийся тем, что разрядность σ случайного многоразрядного двоичного числа w выбирают из условия σ≤ξ.

4. Способ по п.1, отличающийся тем, что предварительно заданный получателю и отправителю информации показатель t выбирают из условия 2≤t≤256.

5. Способ по п.1, отличающийся тем, что для вычисления первого многоразрядного двоичного числа р открытого ключа генерируют первый вспомогательный простой множитель в виде многоразрядного двоичного числа m, генерируют простой множитель γ в виде ξ-разрядного двоичного числа и дополнительное случайное четное многоразрядное двоичное число и затем вычисляют второй вспомогательный простой множитель n в виде случайного многоразрядного двоичного числа n=γu+1, а первое многоразрядное двоичное число р открытого ключа вычисляют как произведение первого m и второго n вспомогательных простых множителей.