Система высокоточной автоматической посадки летательных аппаратов

Система высокоточной автоматической посадки летательных аппаратов

Иллюстрации

Показать все

Реферат

Изобретение относится к системам высокоточной автоматической посадки летательных аппаратов (ЛА) в условиях плохой видимости (далее слепой посадки или ССП) с использованием нескольких навигационных приемников, работающих по сигналам спутниковых радионавигационных систем (СРНС) ГЛОНАСС и GPS.

Известны системы точной посадки воздушных судов на взлетно-посадочную полосу (ВПП), включающие создание магнитного поля путем прокладывания систем наземных электрических проводников, измерение составляющих вектора магнитного поля измерителями, установленными на борту судна, отличающийся тем, что вдоль образующих линий ВПП прокладывают в горизонтальной плоскости большой замкнутый электропроводящий контур, соединяют его с источником переменного тока с частотой ω₁ электрическим проводником, проложенным вдоль осевой линии ВПП, создают магнитное поле током источника, при этом компонента вектора в горизонтальной плоскости и перпендикулярная осевой линии ВПП имеет максимум над осевой линией, а вертикальная составляющая вектора магнитного поля проходит через нуль, внутри большого контура прокладывают в горизонтальной плоскости малый электропроводящий контур, подключают к источнику тока с частотой ω₂, причем проводники контуров прокладывают на определенном расстоянии от торцевых и боковых линий ВПП, измеряют значения векторов магнитных полей с частотами ω₁ и ω₂ бортовыми компонентными магнитометрами, определяют курс, высоту и дальность воздушного судна до ВПП с помощью бортовой ЭВМ и производят точную посадку воздушного судна (RU 2199472 С2, B 64 F 1/00, 27.02.2000).

Недостатком системы является низкая точность наведения летательного аппарата, обусловленная флуктуацией магнитного поля Земли.

Известны также другие системы наведения самолетов, использующих как лазерные лучи, так и электромагнитные волны от источников излучения, установленных непосредственно на посадочной полосе (US 3934250, G 01 S 9/56, 20.01.1976, CN 1235293, G 05 D 1/10, 17.11.1999, IL 82554, G 01 S 5/04, 24.06.1994), обладающие недостаточной точностью наведения летательного аппарата из-за разброса параметров, входящих в них элементов, и подверженностью этих элементов внешним воздействиям.

Наиболее близким по технической сути к предлагаемой системе является пример построения экспериментальной ССП на основе обработки измерений псевдофазы СРНС GPS, предпринятый в Стэнфортском университете США, описанный в "Global Positioning System: Theory and Applications. Volume I, and II. Edited by Parkinson B. W. and Spilker J. J. PROGRESS IN ASTRONAUTICS AND AERONAUTICS, Volume 163. Published by the American Institute of Aeronautics and Astronautics, Inc. 370 L'Enfant Promenade, SW, Washington, DC 20024-2518, 1996" и

"P.Y. Montgomery, D.G. Lawrwnce, and other. UAV Application of IBLS for Autonomus Takeoff and Landing. ION GPS-99, p.1541-1547".

Система, описанная в указанных источниках информации, функционирует следующим образом.

На земле перед взлетно-посадочной полосой (ВПП) располагается система нескольких (от двух до четырех) псевдоспутников (IBLS - Integrity Beacon Landing System), излучающих GPS-подобные сигналы. Мощности излучаемых сигналов таковы, что их захват и сопровождение возможны только при условии, что самолет находится внутри относительно небольших областей (далее пузырей), окружающих каждый из псевдоспутников. Самолет наводится в области, охватываемой "пузырями" (при заходе на посадку) на основе обычной системы кодовой дифференциальной навигации (на основе передачи поправок к измерениям псевдодальностей). Как известно, точность такой системы дифференциальной навигации характеризуется ошибками порядка несколько метров. Опорный приемник дифференциальной подсистемы GPS осуществляет измерения по сигналам спутников и псевдоспутников. Сигналы псевдоспутника попадают на вход опорного приемника по кабелям. Результаты всех измерений передаются на борт самолета с помощью линии связи (скорость передачи 2400-4800 бит/с). На борту самолета располагается навигационный приемник с двумя высокочастотными входами, приемник линии связи и процессор обработки данных измерений. Первый высокочастотный вход навигационного приемника подключен к антенне, располагающейся сверху самолета. Он предназначен для приема спутниковых сигналов. Второй высокочастотный вход навигационного приемника подключен к антенне, располагающейся снизу самолета.

Этот вход предназначен для приема сигналов псевдоспутников. Данные измерений, осуществляемых на борту самолета, а также данные измерений, поступающих на борт по линии связи, совместно обрабатываются в процессоре. С целью определения пространственного положения вектора, соединяющего фазовые центры верхней и нижней антенн самолета необходимо дополнительно привлекать информацию об ориентации самолета. Такая информация может поставляться как системой, работающей по сигналам GPS, так и инерциальной системой (IMU). Самолет, пролетая через "пузыри", проводит измерения, позволяющие ему разрешить неоднозначность псевдофазовых измерений. После выхода из пузырей, прием сигналов на нижнюю антенну прекращается, и определение координат верхней антенны самолета осуществляется по псевдофазовым измерениям этой антенны и псевдофазовым измерениям наземного опорного приемника.

Недостатки системы слепой посадки стендфордского университета

1. Необходимость преодоления проблемы "близко-далеко" ("near-far"). При перемещении самолета дальности до спутников изменяются незначительно и поэтому мощности спутниковых сигналов остаются практически постоянными. Но по отношению к псевдоспутникам то же самое перемещение самолета приводит к значительным изменениям дальностей и, следовательно, к значительному изменению мощности принимаемых сигналов. Резкое различие в динамических диапазонах сигналов спутников и псевдоспутников вызывает значительные трудности в построении приемных устройств.

2. Измерения, позволяющие разрешить неоднозначность псевдофазовых измерений, осуществляются только при прохождении самолета через пузыри. Дальнейшее определение координат верхней антенны самолета осуществляется по псевдофазовым измерениям сигналов, поступающих на эту антенну и псевдофазовым измерениям, осуществляемым наземным опорным приемником. Однако успешное определение координат в таком режиме возможно только при условии непрерывного отслеживания фаз несущих спутниковых сигналов после выхода самолета из пузырей, т.е. при условии сохранения неизменными тех целочисленных неоднозначностей, значения которых были определены бортовым процессором самолета по измерениям, осуществленным при прохождении пузырей. При кратковременных срывах слежения, значения целочисленных неоднозначностей изменяются. Следовательно, если такие срывы появятся на этапе движения самолета после пузырей, то разрешение неоднозначности становится невозможным. В случае возникновения срывов слежения (in the event of detected continuity fault) в [2] рекомендуется располагать псевдоспутники достаточно далеко для того, чтобы иметь возможность сделать новый заход на посадку.

3. При изменении направления ветра могут возникать ситуации, когда посадку более целесообразно осуществлять с другого конца взлетно-посадочной полосы. В такой ситуации наземное псевдоспутниковое оборудование необходимо располагать с обоих концов взлетно-посадочной полосы, т.е. объем наземного оборудования удваивается.

4. Реализация системы слепой посадки Стэндфордского университета требует разработки наземной аппаратуры псевдоспутников, излучающих GPS-подобные сигналы, разработки специального опорного приемника, способного осуществлять прием сигналов спутников и псевдоспутников и разработки специального бортового приемника, способного принимать сигналы на верхнюю и нижнюю антенны самолета.

Технический результат предложенного решения заключается в повышении надежности посадки летательных аппаратов.

Для этого предлагается система высокоточной автоматической посадки летательных аппаратов (ЛА), содержащая навигационные спутники системы ГЛОНАСС и/или GPS и взаимодействующий с ними приемный блок, размещенный на летательном аппарате, а также "п" наземных фазовых навигационных приемников (НП), расположенных рядом с взлетно-посадочной полосой (ВПП), где "n"- целое число больше 3, при этом наземные фазовые навигационные приемники формируют по полученным от навигационных спутников сигналам значения псевдофаз и псевдодальностей на один и тот же момент времени, которые с помощью блока передачи передаются в центр приема и формирования навигационного кадра (ЦПИФНК), где полученные сообщения предварительно обрабатываются для сокращения избыточности и формируется информационный кадр, который по линии связи передается на летательный аппарат, где в вычислительном блоке, соединенном с приемным блоком, сигналы, полученные от всех навигационных спутников, находящихся в пределах видимости, обрабатываются совместно с сигналами наземных фазовых навигационных приемников, полученных по линии связи.

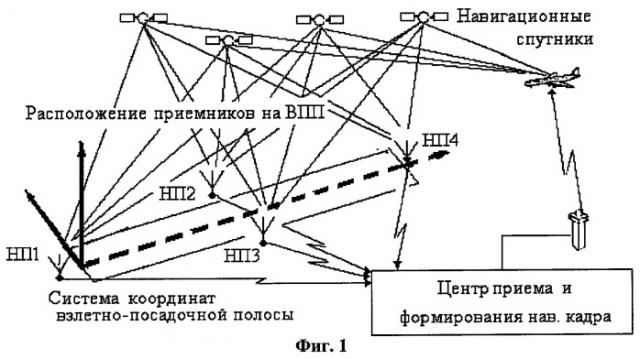
Система высокоточной автоматической посадки летательных аппаратов поясняется на фиг.1. Три или более наземных фазовых навигационных приемников (НП) 1, 2, 3, 4 располагаются рядом с взлетно-посадочной полосой (ВПП), изображенной пунктиром, так, как это показано на фиг.1. Наземные НП принимают сигналы от навигационных спутников (НС) GPS и ГЛОНАСС. Координаты фазовых центров антенн НП в системе координат ВПП определяются геодезическими методами заранее с высокой точностью (с ошибками, не превышающими долей сантиметра). Путем сравнения координат фазовых центров антенн в гринвичской системе и системе координат ВПП находится вектор смещения начала системы координат ВПП относительно начала гринвичской системы, а также матрица перехода из гринвичской системы в систему координат ВПП.

Измерения псевдофазы и псевдодальности, получаемые наземными НП в один и тот же момент времени, передаются в центр приема и формирования навигационного кадра (ЦПИФНК). В ЦПИФНК полученные сообщения предварительно обрабатываются для сокращения избыточности. Далее формируется информационный кадр, который по специальной линии связи ретранслируется на самолет. Информационный кадр включает информацию о "сырых" измерениях псевдодальности, псевдофазы и псевдодопплера, данные альманаха и эфемерид НС, время получения сообщений, признаки качества передаваемых сообщений, координаты наземных НП и другую дополнительную информацию, которая может потребоваться на борту самолета.

На самолете установлен фазовый НП, который формирует измерения по всем видимым НС GPS и ГЛОНАСС. Измерения самолетного НП обрабатываются в специализированном вычислителе совместно с измерениями наземных НП, полученными по линии связи.

Рассмотрим пример расчета местоположения ЛА относительно ВПП.

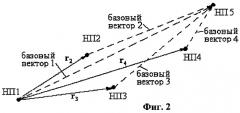
Рассмотрим четыре наземных приемника: НП1, НП2, НП3, НП4 и самолетный приемник НП3, которые ведут одновременно измерения псевдодальностей и псевдофаз. Положим, что вектора r₂, r₃, r₄, соединяющие НП1 соответственно со НП2, НП3, НП4 известны с высокой точностью (см. фиг.2).

Если вектора r₂, r₃, r₄, сложить с вектором х_1,c грубых абсолютных координат НП1, то получим вектора абсолютных координат х_2,c, х_3,c х_4,c

второго, третьего и четвертого приемников, ошибки которых будут с высокой точностью совпадать с ошибками абсолютных координат х_1,c первого приемника. Ставится задача определения в этих условиях координат самолетного приемника по одномоментным измерениям псевдодальностей и псевдофаз, осуществляемых одновременно всеми четырьмя приемниками.

Для простоты рассмотрим пока что измерения только по системе GPS в диапазоне L1. Также ради простоты будем рассматривать приемники, удаленные друг от друга на расстояния, при которых тропосферные и ионосферные искажения компенсируются при образовании вторых разностей псевдодальностей и псевдофаз. Это позволяет не учитывать тропосферные и ионосферные искажения в математических моделях исходных измерений, что, естественно, упростит проведение первого тестового эксперимента с реальными измерениями.

Каждый из приемников формирует измерения псевдодальностей и псевдофаз. С учетом выбранного нами простого случая, математические модели исходных измерений псевдодальностей и псевдофаз, отнесенные к одинаковым показаниям часов всех приемников, могут быть записаны в виде:

где

- i (нижний индекс) обозначает номер приемника. Для удобства обозначений самолетному приемнику присвоен индекс 5;

- j (верхний индекс) обозначает номер спутника;

- J - общее число спутников, отслеживаемых всеми приемниками;

- дальность между i-м приемником и j-м спутником;

- λ=0.19029367279836488 м - номинальная длина волны диапазона LI GPS;

- f=15 75.42 МГц - номинальная частота несущего сигнала L1 GPS;

- ΔТ_i - смещение показаний часов i-го приемника относительно показаний часов системы на момент измерения;

- ΔТ^j - смещение показаний часов j-го спутника относительно показаний часов системы на момент предшествия моменту измерения;

- Т_hi - задержка кодового сигнала в аппаратуре i-го приемника;

- - задержка кодового сигнала i-го приемника, вызываемая многолучевыми искажениями;

- - ошибка слежения за кодовым сигналом;

- ψ_o,i - неопределенная начальная фаза i-го приемника;

- - неопределенная начальная фаза j-го спутника;

- ψ_hi - фазовые аппаратурные искажения в i-м приемнике;

- - многолучевые искажения сигнала несущей j-го спутника в i-м приемнике;

- - ошибки слежения за фазой несущего сигнала j-го спутника в i-м приемнике;

- - неопределенное целое число, отображающее неоднозначность измерений псевдофазы j-го спутника в i-м приемнике. Используя исходные математические модели (2) и (3), найдем модели для первых разностей псевдодальностей и псевдофаз, соответствующих каждому из четырех базовых векторов, показанных на фиг 2:

где ΔT_hi=T_h5-T_hi, , , , Δψ_o,i=ψ_o,5-ψ_ro,i, , , , . Образование первых разностей (4), (5) по каждому j-му спутнику осуществляется путем вычитания измерений приемника с номером i из измерений самолетного приемника (имеющего в наших обозначениях номер 5). Номера базовых векторов и номера, соответствующих им первых разностей (4), (5) равны номерам приемников, измерения которых вычитаются из измерений самолетного приемника.

Выберем для всех четырех базовых векторов общий опорный спутник, который будем обозначать верхним индексом rf (reference), и образуем для каждого базового вектора вторые разности псевдодальностей и псевдофаз:

где , , , , , , , , , j≠rf.

Линеаризация моделей для первых и вторых разностей и представление их в матричном виде

Уравнения для вторых разностей (6) и (7) являются нелинейными. В общем случае такие уравнения решаются методом последовательных приближений или итераций от некоторого грубого начального значения. На каждой итерации формируется система линейных уравнений относительно поправок к решению, найденному на предыдущей итерации. В качестве грубого начального значения в нашем случае можно принять координаты самолетного приемника x_5,c, у_5,c, z_5,с, получаемые в нем путем обработки измерений псевдодальностей.

Нелинейность уравнений для вторых разностей псевдодальностей и псевдофаз (6), (7) порождается нелинейной зависимостью дальности до спутников от координат самолетного приемника х₅, у₅, z₅

где х^j, у^j, z^j - координаты j-го спутника на момент предшествия моменту измерения. Раскладывая (8) в ряд Тейлора в точке с грубыми координатами самолетного приемника x_5,c, у_5,c, z_5,с, найденными на основе обработки измерений псевдодальностей, и ограничиваясь членами в степени не выше первой, получаем:

где

грубая дальность до j-го спутника,

направляющие косинусы вектора, ориентированного из точки грубого положения самолетного приемника на j-й спутник, Δx=x₅-x_5,c, Δу=у₅-у_5,c, Δz=z₅-z_5,c - поправки к грубым координатам х_5,c, y_5,с, z_5,с самолетного приемника. Величины поправок Δх, Δу, Δz не будут превышать значений несколько десятков метров, т.е. они всегда существенно меньше дальностей до спутников. Поэтому приближение (9) является очень точным. В этой связи, при решении систем нелинейных уравнений для вторых разностей достаточно совершить только одну итерацию.

Подставляя аппроксимацию (9) в уравнения для вторых разностей псевдодальностей (6) и псевдофаз (7), получаем следующие линеаризованные выражения:

где , , j≠rf

Введем следующие векторно-матричные обозначения:

где

невязки вторых разностей псевдодальностей и псевдофаз на момент измерения,

где

ошибки определения вторых разностей псевдодальностей и псевдофаз,

где

неопределенные целые, входящие в выражения (13),

вектор оцениваемых параметров.

С учетом обозначений (14-28), линеаризованные выражения для вторых разностей псевдодальностей и псевдофаз (12), (13) могут быть переписаны в следующем матричном виде:

Выражения (29-30) перепишем в общем виде:

где

Вычисление максимально правдоподобной оценки

В предположении нормальности распределения вектора ошибок Ξ, максимально правдоподобное значение оцениваемого параметра ΔΘ вычисляется по формуле:

где B=R^-1, R - ковариационная матрица ошибок определения вторых разностей псевдодальностей и псевдофаз, вычисляемая в следующем разделе,

где - целочисленный вектор, минимизирующий в целых числах квадратичную форму

Матрицы D_ϕ, D_ϕγ - являются подматрицами матрицы

Вычисление ковариационной матрицы R ошибок определения вторых разностей псевдодальностей и псевдофаз

Будем полагать, что исходные измерения псевдодальностей и псевдофаз являются независимыми и равноточными по всем спутникам. Поскольку вектора вторых разностей псевдодальностей γ и вторых разностей псевдофаз ϕ формируются из исходных измерений независимо, искомую матрицу R можно представить в виде:

где R_γ, R_ϕ - ковариационные матрицы ошибок определения вторых разностей псевдодальностей и псевдофаз соответственно.

Вычисление ковариационных матриц R_γ, R_ϕ осуществляется аналогично. Поэтому рассмотрим вычисление только одной из этих матриц, например R_ϕ. Введем в рассмотрение ковариационную (J×J)-матрицу Rp исходных измерений псевдофазы i-м приемником. Поскольку мы полагаем, что измерения псевдофазы всеми приемниками по всем путникам равноточные, то матрица Rp будет диагональной. По ее главной диагонали будут располагаться дисперсии ошибок исходных измерений псевдофазы. Тогда матрица исходных измерений псевдофазы всеми приемниками по всем спутникам может быть представлена в следующем блочном виде:

Из правила образования первых разностей псевдофаз (5) видим, что вектор первых разностей может быть образован из вектора исходных измерений путем умножения на матрицу, которая может быть представлена в следующем блочном виде:

где I - единичная (J×J)-матрица. Тогда ковариационная матрица первых разностей псевдофаз R1_ϕ может быть вычислена следующим образом [1]:

Вторые разности псевдофаз образуются только из первых разностей, относящихся к определенной базовой линии. Поэтому матрица формирования общего вектора вторых разностей из общего вектора первых разностей имеет вид:

где Tr₂(J-1)×J - матрица, образуемая из (J-1)×(J-1) - единичной матрицы путем вставки в нее столбца, состоящего из - 1, на место, определяемое номером опорного спутника. С учетом (42), искомая ковариационная матрица вторых разностей псевдофаз R_ϕ может быть вычислена так [1]:

Если в (43) под матрицей Rp понимать ковариационную матрицу исходных измерений псевдодальностей i-м приемником, то с помощью (43) может быть вычислена и ковариационная матрица R_γ ошибок определения вторых разностей псевдодальностей.

Оценка вероятности правильного разрешения неоднозначности в предлагаемой системе посадки

Ясно, что характеристикой, которая будет определять возможность практического построения предлагаемой системы, является вероятность правильного разрешения неоднозначности псевдофазовых измерений. Указанная вероятность будет определяться свойствами матрицы D_ϕ в квадратичной форме (35). Учитывая, что ковариационная матрица R ошибок определения вторых разностей псевдодальностей и псевдофаз может быть представлена в блочно-диагональном виде (38), получаем, что обратная к ней матрица В=R^-1 будет иметь также блочно-диагональный вид:

где , . Используя (44), нетрудно вычислить блок D_ϕ матрицы D (37):

Из представления (20) матрицы Hf_ϕ, которая определяет свойства матрицы D_ϕ, видим, что структура расположения наземных приемников никак не проявляется в матрице Hf_ϕ. Проявляется лишь количество наземных приемников, которое отражается в том, что матрица Hf_ϕ содержит четыре одинаковых блока Н_ϕ (21). Элементы блока Н_ϕ зависят только от координат самолетного приемника и координат спутников, по которым осуществляются измерения, и никак не зависят от расположения наземных приемников. Отсюда можно сделать вывод, что геометрия расположения наземных приемников никак не будет влиять на вероятность правильного разрешения неоднозначности. Влияние на эту вероятность будет оказывать только количество наземных приемников. Таким образом, применение дополнительных наземных приемников приводит лишь к усреднению ошибок измерений, в результате чего происходит повышение надежности правильного разрешения неоднозначности.

Для того чтобы обосновать последний вывод более формально, пренебрежем корреляцией ошибок определения вторых разностей псевдодальностей и псевдофаз, вызываемой использованием во всех вторых разностях общих измерений самолетной антенны. Пренебрежение этой корреляцией не может значительно повлиять на вероятность правильного разрешения неоднозначности. В этих условиях ковариационная матрица ошибок вторых разностей псевдофаз R_ϕ (43) становится блочно-диагональной и, следовательно, блочно-диагональный вид приобретет матрица В_ϕ=R^-1 _ϕ. С учетом блочного вида матрицы Hf_ϕ (20), получаем, что и матрица D_ϕ (45) также приобретает блочно-диагональный вид:

где

матрица квадратичной формы в целых числах, соответствующей отдельной базовой линии. Аналогично нетрудно показать, что матрица D_ϕγ, входящая в выражение (36) при пренебрежении корреляцией ошибок во вторых разностях также может быть представлена в блочно-диагональном виде. Из блочно-диагонального вида матриц D_ϕ и D_ϕγ следует, что при пренебрежении корреляцией ошибок определения вторых разностей псевдодальностей и псевдофаз, квадратичная форма d(k) (35) представляется в виде суммы

где d_i(k), квадратичные формы, соответствующие каждому из четырех базовых векторов, k_i-целочисленные подвекторы общего вектора k, также соответствующие своим базовым векторам. Таким образом, видим, что при пренебрежении корреляцией ошибок определения вторых разностей псевдодальностей и псевдофаз, минимальное значение квадратичной формы d(k) (35), которое определяет вероятность правильного разрешения неоднозначности, может быть вычислено как минимум суммы из четырех квадратичных форм, каждая из которых соответствует своему базовому вектору. В процессе такого суммирования и происходит усреднение ошибок исходных измерений псевдодальностей и псевдофаз. На это же указывают и четыре одинаковых блока Н_ϕ матрицы Hf_ϕ. (20). Каждый из этих блоков порождает четыре одинаковые пространственные решетки, образуемые плоскостями, задаваемыми строками блоков Н_ϕ (21). Поскольку все блоки Н_ϕ в составе матрицы Hf_ϕ одинаковы, решетки будут порождаться системами параллельных плоскостей. Смещение параллельных плоскостей, принадлежащих разным решеткам, друг относительно друга будет определяться различием ошибок измерений. Наложение друг на друга таких решеток эквивалентно введению одной решетки, в которой каждые четыре параллельных плоскости, принадлежащих разным решеткам, заменяются одной средней плоскостью.

1. Достижение высокой надежности правильного разрешения неоднозначности в системе, осуществляющей усреднение измерений наземных приемников, возможно только при значительном увеличении точности усредненных измерений. Поэтому в системе слепой посадки необходимо использовать двухчастотные приемники. Предстоящее введение в ближайшие годы гражданских сигналов на второй частоте в обеих системах GPS и ГЛОНАСС сделает двухчастотные приемники практически столь же дешевыми и доступными, как и одночастотные. Поэтому стоимость системы посадки на основе двухчастотных приемников не будет значительно превышать стоимость варианта ее построения на основе одночастотных приемников.

2. Применение нескольких наземных приемников (например, четырех) позволит с одной стороны увеличить вероятность правильного разрешения неоднозначности, а с другой стороны увеличить надежность функционирования аппаратуры посадочного комплекса, что само по себе очень важно.

3. Обработка измерений псевдодальностей и псевдофаз, полученных от двухчастотных приемников, может осуществляться на основе вышерассмотренного алгоритма.

4. Вместе с тем, следует отметить, что увеличение количества неоднозначных измерений, включаемых в обработку, увеличивает требования к быстродействию процессора. Однако опыт использования известных в настоящее время алгоритмов разрешения неоднозначности показывает, что успешное решение задачи достигается при включении в обработку до 200 неоднозначных измерений. Как видим, количество неоднозначных измерений, которое одновременно придется обрабатывать в альтернативной системе посадки значительно меньше 200. Отсюда можно сделать вывод, что обработка учетверенного числа неоднозначных измерений в альтернативной системе посадки вполне под силу современным процессорам.

Система высокоточной автоматической посадки летательных аппаратов (ЛА), содержащая навигационные спутники системы ГЛОНАСС и/или GSP и взаимодействующий с ними приемный блок, размещенный на летательном аппарате, а также n наземных фазовых навигационных приемников (НП), расположенных рядом со взлетно-посадочной полосой, где n - целое число больше 3, при этом наземные фазовые навигационные приемники формируют по полученным от навигационных спутников сигналам значения псевдофаз и псевдодальностей на один и тот же момент времени, которые с помощью блока передачи передаются в центр приема и формирования информационного кадра (ЦПИФНК), где полученные сообщения псевдофаз и псевдодальностей предварительно обрабатываются для сокращения избыточности и формируется информационный кадр, который по линии связи передается на летательный аппарат, где в вычислительном блоке, соединенном с приемным блоком, сигналы, полученные от всех навигационных спутников, находящихся в пределах видимости, обрабатываются совместно с сигналами наземных фазовых навигационных приемников, полученных по линии связи.